计入齿圈螺栓约束的行星齿轮箱振动模型研究
2023-07-27杨秋平李志强
杨秋平,李志强
(1.新乡职业技术学院,河南新乡 453000;2.郑州大学机械与动力工程学院,河南郑州 450001)
0 前言
行星齿轮箱在机械传动过程中具有传动比大、结构紧凑等优点,被广泛应用于航空航天、汽车、风力发电等领域[1-2]。一般来说,太阳齿轮和行星架分别为输入和输出元件,齿圈固定在底座上,行星齿轮随行星架转动,各行星齿轮与太阳齿轮和齿圈齿轮同时啮合,分别形成外啮合齿轮副和内啮合齿轮副。
行星齿轮箱的振动信号复杂,为了更好地理解齿轮箱的振动机制,国内外研究学者对齿轮箱振动模型进行了大量的研究。MOSHREFZADEH、FASANA[3]在动态模型中加入了故障轴承模型,研究表明集总参数模型在考虑影响振动响应的非线性因素方面具有一定的优势。XUE、HOWARD[4]建立了行星齿轮箱多自由度扭转振动模型,结果表明该模型可以作为行星齿轮箱故障诊断的有效工具。杨占力等[5]通过集总参数模型研究了动态参数对行星齿轮箱的振动影响,比较了不同负载和转速下的行星齿轮箱振动特性。吴守军等[6]建立了计入啮合线方向的行星齿轮系统振动响应模型,分析了啮合线相对位移及频谱特性,该模型能有效提取行星齿轮系统的啮合频率和故障频率,并通过实验验证了所提模型的合理性。王成龙等[7]建立了计入部件平移-扭转的行星齿轮系统动力学模型,通过该模型研究了不同初始条件下内齿圈的振动特性。魏静等人[8]建立了计入时变啮合刚度等因素的行星齿轮传动动力学模型,分析了不同时变位姿参数对振动响应特性的影响,该模型能够为可靠性设计提供一定的数据支撑。林祖胜、张绍辉[9]建立了行星齿轮传动系统有限元模型,仿真了内齿圈振动特性,并对比了实验过程中的模态特性,结果表明所建立的仿真模型具有一定合理性。王二化等[10]通过建立多传感器信号模型,解决了单一传感器振动信号的不稳定性问题,通过小波分解的方法实现了各频段能量的提取,分析了不同载荷等因素对频道能量的影响,该方法能够为齿轮箱结构的合理性设计提供参考依据。
本文作者在前人研究基础上,提出一种基于齿轮箱结构参数的新方法,该方法在传统方法的基础上,利用振动位移计算内齿轮副的啮合力。根据欧拉-伯努利梁理论,计算齿圈在啮合力作用下的振动信号。该模型考虑齿圈的螺栓约束,且建模方法不需要考虑窗函数、振动分量的贡献等,可以有效地避免主观性问题。
1 齿轮箱振动啮合特性
齿轮箱振动主要是由齿轮副啮合、齿轮和轴承失效、轴不对中等引起。振动信号通过不同传输路径将不同振动源传输到同一传感器。因此,传感器信号中不同分量的贡献不同。由于传感器一般安装在齿圈上,内齿轮副(行星齿圈副)的啮合力Frpn(n=1,2,…,N)可以通过式(1)得到:
Frpn=krpn·δrpn
(1)
式中:krpn和δrpn分别为第n个内齿轮副的啮合刚度和变形量,可根据势能法和集中参数模型求解。
为了探讨Frpn(n=1,2,…,N),首先研究了齿轮箱齿轮副的啮合刚度kspn和krpn。以3个行星齿轮变速箱为例,其基本参数如表1所示。由于3个行星齿轮与太阳齿轮和环齿轮同时啮合,齿轮箱总共包含6个齿轮副,其刚度曲线和啮合相位分别如图1和表2所示,图中绿色的点表示齿轮副的节点,每条刚度曲线在一个啮合周期内出现两次突变。由于相位因素,这些突变不会同时发生。

图1 外齿轮副(a)和内齿轮副(b)的啮合刚度曲线

表1 行星齿轮箱物理参数

表2 行星齿轮箱啮合相位
刚度的突变是一种内部激励,影响齿轮副的啮合力。以啮合力Frp1为例,其曲线如图2所示,可以看出:曲线以Tm为周期,一个啮合周期存在很多衰减振荡信号。对比图2和图1可以发现:这些衰减信号对应于内外齿轮副的突变,且内齿轮副产生的冲击幅值高于外齿轮副。
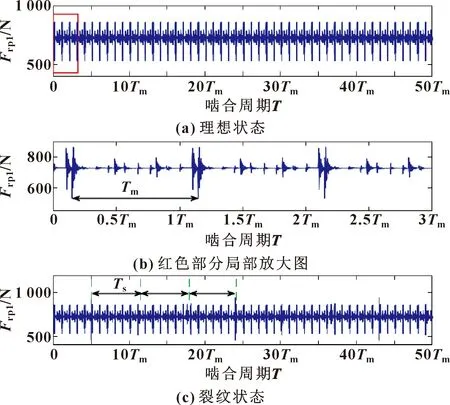
图2 第一内齿轮副啮合力Frp1
图2(c)为太阳齿根处出现2 mm深度齿裂纹时的力Frp1曲线,与图2(a)相比,出现了一系列与裂纹有关的断层,即尽管失效发生在太阳齿轮(形成外齿轮副),但仍然影响内齿轮副的啮合力。因此每个振动部分的振动信息相互重叠。
2 齿轮箱振动信号模型
2.1 基于欧拉-伯努利梁理论的振动模型
由于行星架的转动,行星齿轮箱的振动信号具有明显的幅度调制,采用Hanning或Hamming窗对其进行模拟[11]。这些窗口函数的参数都是人为选择的,与变速箱的基本结构参数无关,振动信号的幅值会随着被测位置的变化而变化。以图3中的齿轮箱为例,环形齿轮通过8个螺栓与两侧的底座连接,这些螺栓将环形齿轮划分为多个区域。当振动源和传感器位于不同区域时,螺栓可能会影响振动信号的有效传递,因此此研究在建立传感器信号模型时将考虑这些螺栓,以螺栓为边界,将环齿轮分为8个部分。齿轮箱顶部安装振动加速度传感器,与A零件相对应,最靠近螺栓8的行星齿轮设置为行星齿轮1,后续将研究行星齿轮1随行星架顺时针旋转一个周期时传感器的振动加速度信号。

图3 行星变速箱结构模型
齿圈齿的几何形状主要影响齿轮副的啮合刚度,反映在啮合力上如图2所示。将A部分的齿圈简化为两端有支撑的欧拉-伯努利梁,如图4所示。以8号螺栓为原点,建立坐标系Oxy。长度l表示螺栓8和螺栓1之间的齿圈弧长。假设行星架的旋转方向为顺时针,可以认为啮合力的方向Frp1恒定,啮合点以v=ωc·rr的速度沿着x方向从螺栓8移动到螺栓1,其中ωc为行星架的转速,rr为齿圈的节圆半径。此外,啮合力Frp1在切向和径向上可分解为Frp1x和Frp1y,其中Frp1y=Frp1·sinα,α为齿圈在节圆上的压力角。此研究在理论建模中只考虑径向力Frp1y。采用力密度函数f(x,t)表示t时刻的啮合力Frp1y,其中在x截面处有x=v·t,则有:

图4 齿圈截面受力示意简图
f(x,t)=Frp1y·δ(x-v·t)
(2)
其中:δ为狄拉克函数。简化后的齿圈截面如图4所示,b和h分别为齿圈的宽度和高度。在位置x的齿圈厚度h(x)受齿轮齿几何形状的影响,当h(x)为非均匀时,x位置处截面的截面面积A(x)、转动惯量I(x)等将发生变化。这些变量可以看作是内部激励,会影响x位置的振动幅值,从而增加了齿圈振动信号的复杂性,但振动信号的包络趋势不会发生明显变化。因此,为了简化,此研究提出采用常数h代替不均匀厚度h(x),并选择齿圈最薄部分的厚度。齿圈的测量结果表明,齿圈的有效厚度h=9.4 mm,宽度b=53 mm。
在图4中,K和Kt分别为A部分受2个螺栓约束后的径向支撑刚度和扭转刚度。此研究螺栓的径向刚度和扭转刚度应与简化欧拉-伯努利梁的轴向刚度和弯曲刚度一致,设置刚度K=E·A和Kt=E·I来模拟梁在这2个螺栓处的平移和转动。图4显示了齿圈的力的微小段dx的示意,沿y方向运动的微分方程表示为
(3)
其中:Q为剪切力;M为弯矩;ρ为齿圈的材料密度;A为截面面积。从而可以计算出t时刻齿圈零件x位置的加速度信号,如式(4)所示:
(4)
其中:i为振动模态的阶数,文中取前3个阶数。当不考虑齿圈与传感器之间的传输衰减时,x位置齿圈的振动信号可以表示传感器安装在该位置时的传感器信号。由式(4)可知,位置x处的信号模型可以考虑影响传感器信号的各种因素,A部分齿圈截面的基本参数如表3所示。
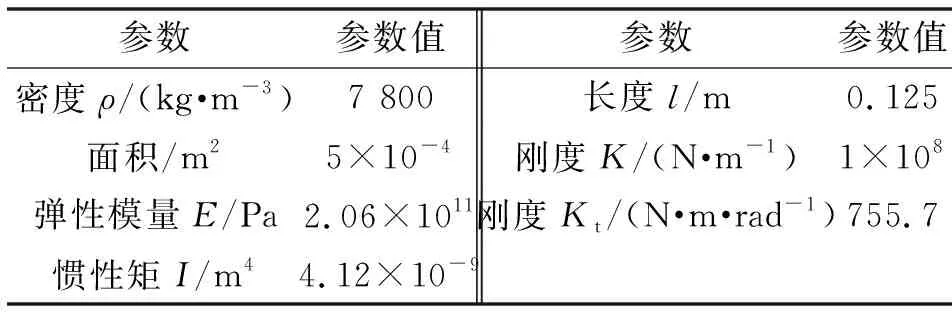
表3 截面A齿圈基本参数
当行星齿轮继续旋转,啮合点将通过螺栓1进入B部分区域,部分啮合点在B部分的环形齿轮简化如图5所示。
图5 啮合力在区域B时齿圈的简化示意
根据欧拉-伯努利梁理论,可以得到环齿任意一点的振动,式(5)(6)分别表示任意位置的广义力和振动加速度:
(5)
d4·cosh(0.5βil)]·{cos(ωit)·[d0sin(βix)+d2cos(βix)+d3sinh(βix)+d4cosh(βix)]}
(6)
根据式(4)(6),行星齿轮1通过A、B部分时模拟的传感器信号如图6所示,可以看出:由于螺栓的作用,在两端和第10齿附近的振动信号波动较大,幅度相对较小。振动加速度幅值在第10个齿后处于较低水平。A部分和B部分的振动信号最大幅值分别为Apart A=0.172 m/s2,Apart B=0.056 9 m/s2,这进一步证明了环形齿轮螺栓对振动信号有明显的抑制作用。
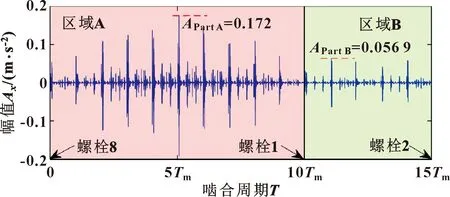
图6 啮合点从螺栓8移动到螺栓2时的模拟传感器信号
当行星齿轮1的啮合点通过更多的螺栓时,传感器采集到的振动信号振幅进一步降低到小于0.056 9 m/s2。通常齿轮箱中的几个行星齿轮等距,当前一个行星齿轮的啮合点远离传感器时,后一个行星齿轮的啮合点接近传感器。因此,行星齿轮1在此期间产生的振动信号可视为噪声。考虑到行星齿轮的重复性,其他行星齿轮产生的振动信号也可根据式(4)(6)计算,这些行星齿轮之间的相位差为Zr/N,它们产生的信号可以叠加,从而得到多行星齿轮齿轮箱的仿真振动信号。
2.2 变速箱振动信号模型
一般多个齿轮的加速度信号是在基于集中参数模型的微分方程求解后选择的,并对它们给出不同的贡献来建立最终的振动信号,此研究采用权重来反映各个齿轮的整体传输路径效应,如式(7)所示:
(7)
太阳齿轮、行星齿轮和环形齿轮的整体传动路径效应可以分别用式(8)[12]表示:
(8)
为了模拟载波的调幅效果,与传统方法不同,此研究在建立齿圈振动信号时选择了旋转部件的振动变形而不是振动加速度,传统方法和新方法的流程如图7所示,可以看出:该方法避免了振动分量权重、窗函数等主观步骤。
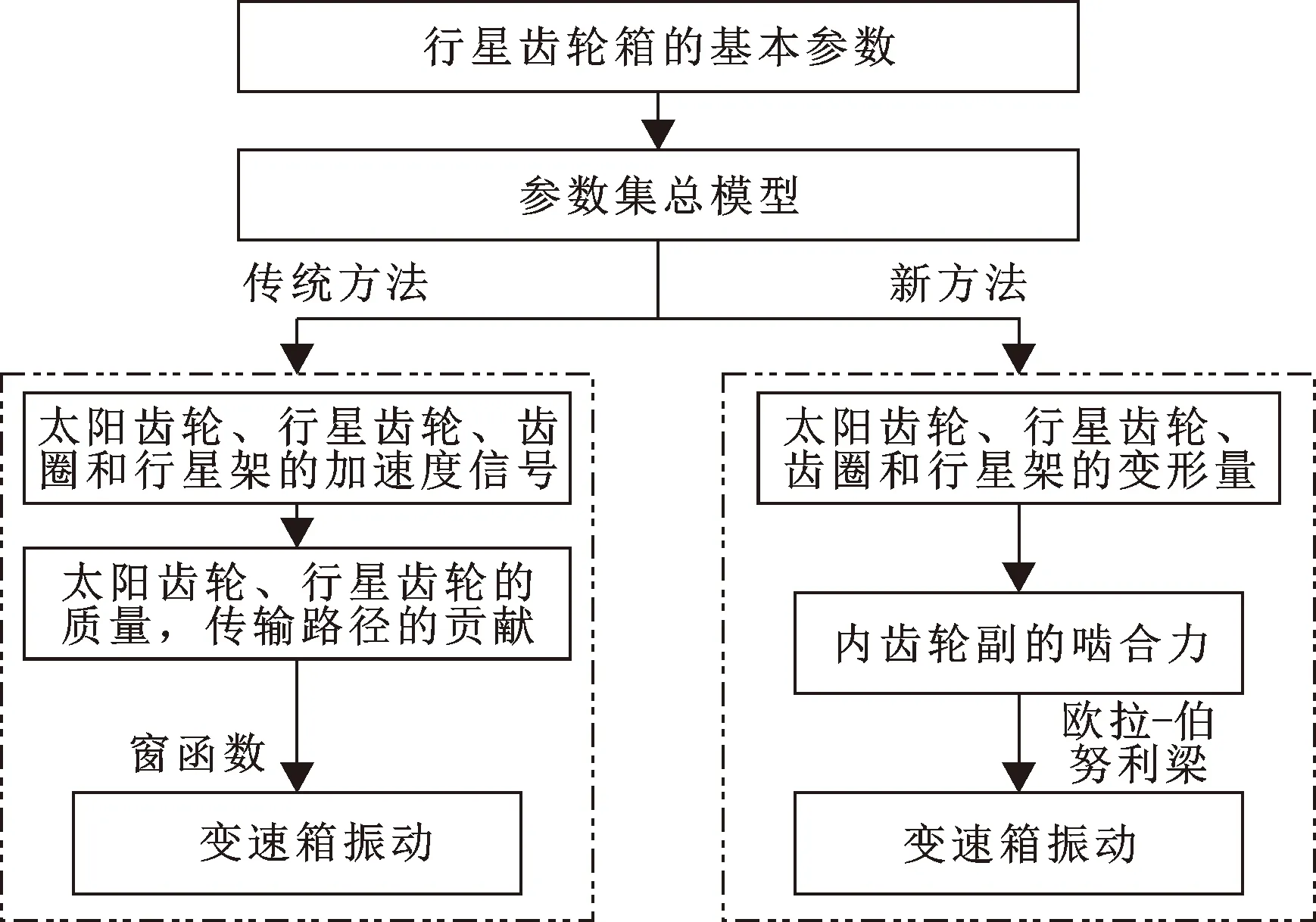
图7 新方法和传统方法的流程
图8分别是基于传统方法[12]和此研究提出的新方法得到的齿轮箱振动曲线。图中红色曲线是振动信号的包络线,可以看到2种方法得到的振动信号都表现出明显的幅度调制现象。在一个行星架旋转周期内,信号波动3次。但在这2种情况下,产生波动调制现象的原因不同。在图8(a)中,直接由Hanning窗生成,在图8(b)中,采用考虑螺栓约束的方程计算。可以看出图8(b)中的红色包络曲线比Hanning窗或Hamming窗更能反映行星架引起的调幅效果。

图8 行星架一圈内的振动信号
此外,这些波动之间还出现了文献[13]中提到的重叠现象,如图8(b)所示。图9所示为图8(b)振动信号在噪声情况下的包络阶谱。振幅较大的阶数出现在低频、啮合阶数及其谐波阶数等处,振动信号的主要频率成分与文献[12]中的模拟和实验信号一致。调制频率是行星架旋转频率的N倍(N=3),啮合阶(Zr=62)的幅值为0,较大的幅值对应于第60阶(Zr-2)和第63阶(Zr+1),与啮合阶相邻。这是因为环形齿轮的齿数Zr不是行星齿轮数N的倍数,导致啮合频率由行星架的旋转频率调制[14]。基于上述时域和频域分析,文中提出的齿轮箱振动信号模型是正确的。

图9 含噪声振动信号的包络阶谱
3 齿轮箱振动信号特征分析
3.1 振动路径传输机制
由于行星齿轮箱结构复杂,振动信号的路径可以分为2种:齿轮箱内部的路径和沿齿轮箱的路径,如图10(a)所示。传感器直接安装在齿圈上时,沿齿轮箱的路径主要是传递齿圈副产生的振动信号,这些信号在传输过程中可能会有很大的衰减,且这些路径的长度是时变的。

图10 传输路径
考虑到来自齿轮箱内部部件的振动信号可能会使传感器信号冗余,此研究不考虑图10(a)中的传动路径,只分析沿变速箱的路径。以图10(b)中啮合点A的振动信号为例,将齿圈传动路径分为路径1(顺时针方向,粉色箭头表示)和路径2(逆时针方向,蓝色箭头表示)。
以图11中行星齿轮箱的啮合状态为例,当振动源位于传感器的左侧,路径1比路径2短,路径1贡献更多,如图11(a)所示。相反,路径2的贡献较大,如图11(c)所示。当两条路径的长度相等时,两条路径的贡献相同,如图11 (b)所示。由于螺栓锚杆对振动信号的传输有明显的抑制作用,因此,此时图(a)中路径2、图(c)中路径1、图(b)中路径1、2不能有效传输振动信号。

图11 传动路径
3.2 螺栓约束效应
传感器采集到的振动信号的幅值受到许多因素的影响,如工作速度、负载、健康状况和变速箱的尺寸等。下面将通过改变螺栓与传感器之间的距离,以及改变螺栓的数量来研究螺栓对信号的影响。
3.2.1 螺栓与传感器之间的距离
为了模拟传感器与螺栓之间不同距离,此研究将传感器的安装位置改变3次。选取图3中齿圈的第1、第3、第5这3个齿位置,传感器安装示意如图12所示。这3个位置分别标记为a1、a3、a5,如图13(a)所示,图中横坐标范围为62Tm,表示行星架旋转一圈。图中这些曲线都显示了3个显著的幅度调制。这是因为在行星架的一个旋转周期中,3个行星齿轮依次靠近和离开传感器。

图12 三个传感器在齿圈上的安装位置
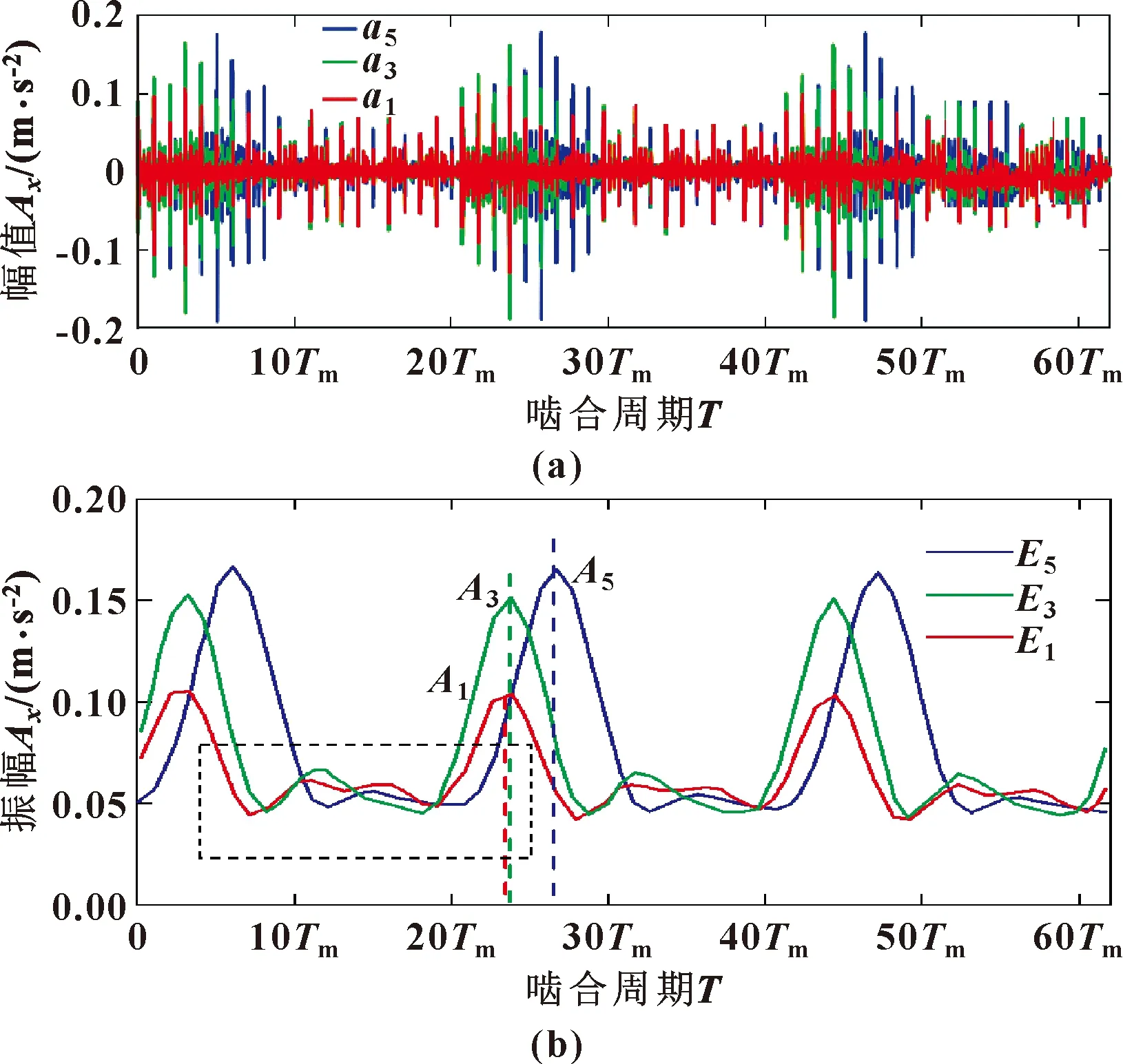
图13 传感器安装在不同位置时的
如图13(b)所示为振动信号的包络曲线Ei(i=1,3,5)和最大幅值Ai(i=1,3,5),可以看出:这些曲线的形状相似,但最大幅值和幅值位置不同。离8号螺栓最远的第5齿的振动信号幅值A5最大,离8号螺栓最近的第1齿的振动信号幅值A1最小。3条曲线最大振幅对应的位置靠近右侧,从而可以看出振动信号的幅值随着传感器与螺栓之间距离的减小而减小。因此,为了得到振幅较大的振动信号,传感器应尽可能远离齿圈的螺栓。
图14所示为图13(b)虚线矩形框中曲线的部分放大图,表示振动信号的重叠区域。这3种情况下重叠区域的振幅和长度也不同,但差异并不显著。原因是虽然传感器的位置发生了变化,但螺栓8和1之间的齿圈的弧长保持不变。由此可见,齿圈螺栓与传感器之间的距离对振动信号的调幅影响较大,但对重叠区域的信号影响较小。
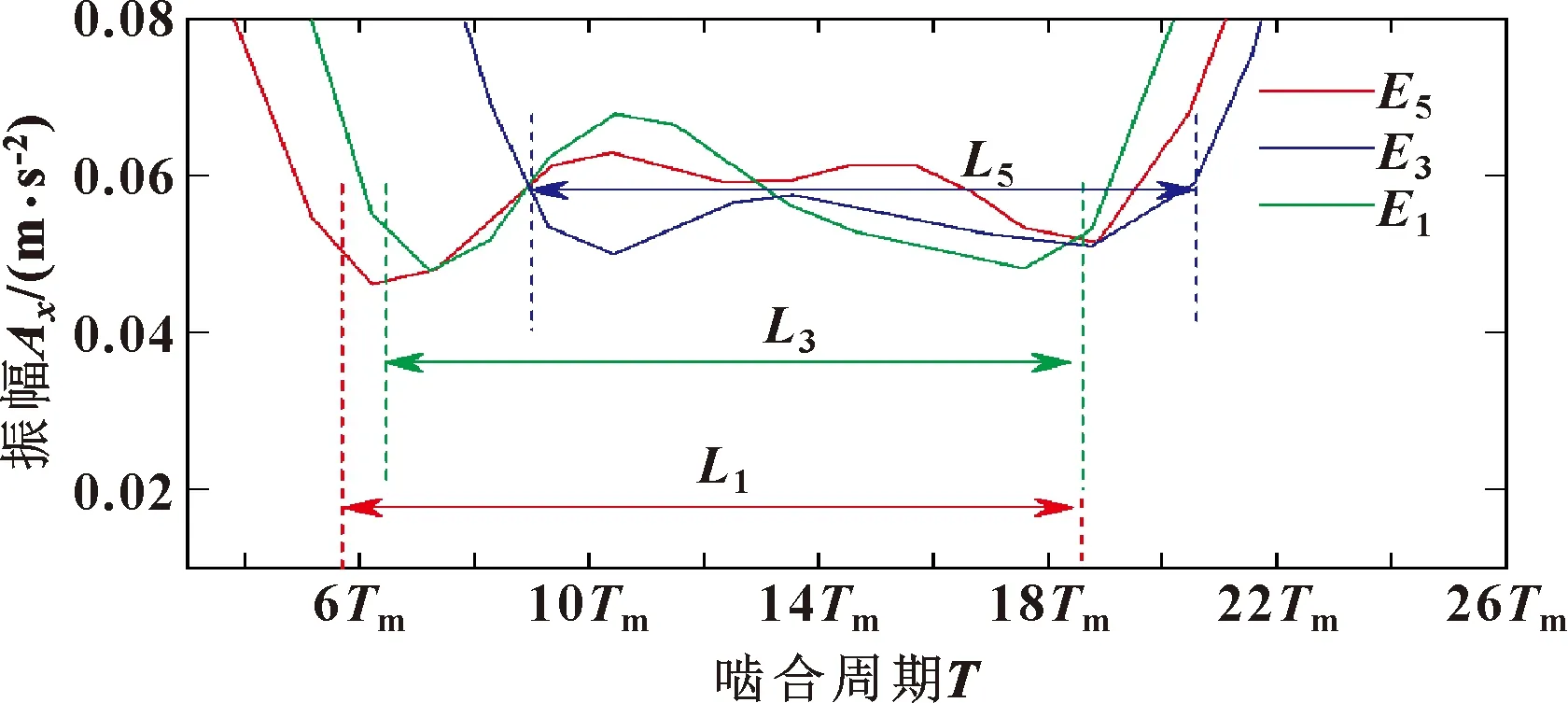
图14 包络曲线重叠区域的比较
3.2.2 螺栓约束数量
为了进一步验证螺栓约束对振动信号的影响,此研究改变了图3中齿圈的螺栓数量,并将传感器保持在A部分的中部。初始状态记为Case 1,且全部螺栓工作;拆下螺栓1,状态变成Case 2;当螺栓1和8都被拆除时,状态变成Case 3。螺栓约束的3种状态如图15所示,改变螺栓约束后,图4中简化的齿圈弧长l发生变化,即lCase1≈10×Tm,lCase2≈15×Tm,lCase3≈20×Tm。

图15 螺栓约束的3种状态
3种情况的振动加速度曲线及其包络曲线如图16所示。可以看出:随着螺栓数量的移除,振幅依次增大(ACase 3>ACase 2>ACase 1),如表4所示,这种变化是由于拆卸螺栓引起的。拆除部分螺栓后,两行星齿轮之间的夹角(φ=2π/N)可能小于相邻两螺栓之间弧长对应的夹角,导致螺栓原本抑制的振动被释放。此外,在Case 1和Case 3中出现最大振幅的位置重合,并且Case 2向右倾斜。这是因为螺栓相对于Case 1和Case 3中的传感器是对称的,而在Case 2中,传感器更靠近左侧的螺栓,这与之前螺栓与传感器之间的距离对振动信号的影响的结论一致。从这些模拟结果可以看出,螺栓约束的数量会影响振动信号的振幅调制。

图16 不同螺栓约束下振动信号(a)

表4 不同螺栓约束下的振幅和长度
虚线矩形框的部分放大视图如图17所示,从表4可以看出:这3种情况下重叠区域的长度和振幅都不相同,最大重叠长度LCase 1和最小重叠长度LCase 3分别对应Case 1和Case 3,这种变化也是由螺栓的拆除引起。任意2个行星齿轮之间的齿圈弧长为LPP≈21×Tm。当齿轮箱约束状态为Case 1时,螺栓8与螺栓1之间的弧长为LCase 1≈10×Tm,因此重叠区域的长度为LCase 1≈11×Tm。同样当齿轮箱在Case 2和Case 3时,可以得到重叠区域的长度分别为6×Tm和1×Tm。但重叠区域的振幅BCase i(i=1,2,3)的趋势与长度的趋势相反,这些变化也是由拆除螺栓引起的。但由于实际振动信号不可避免地包含噪声,重叠区域可能会被其他干扰成分覆盖。
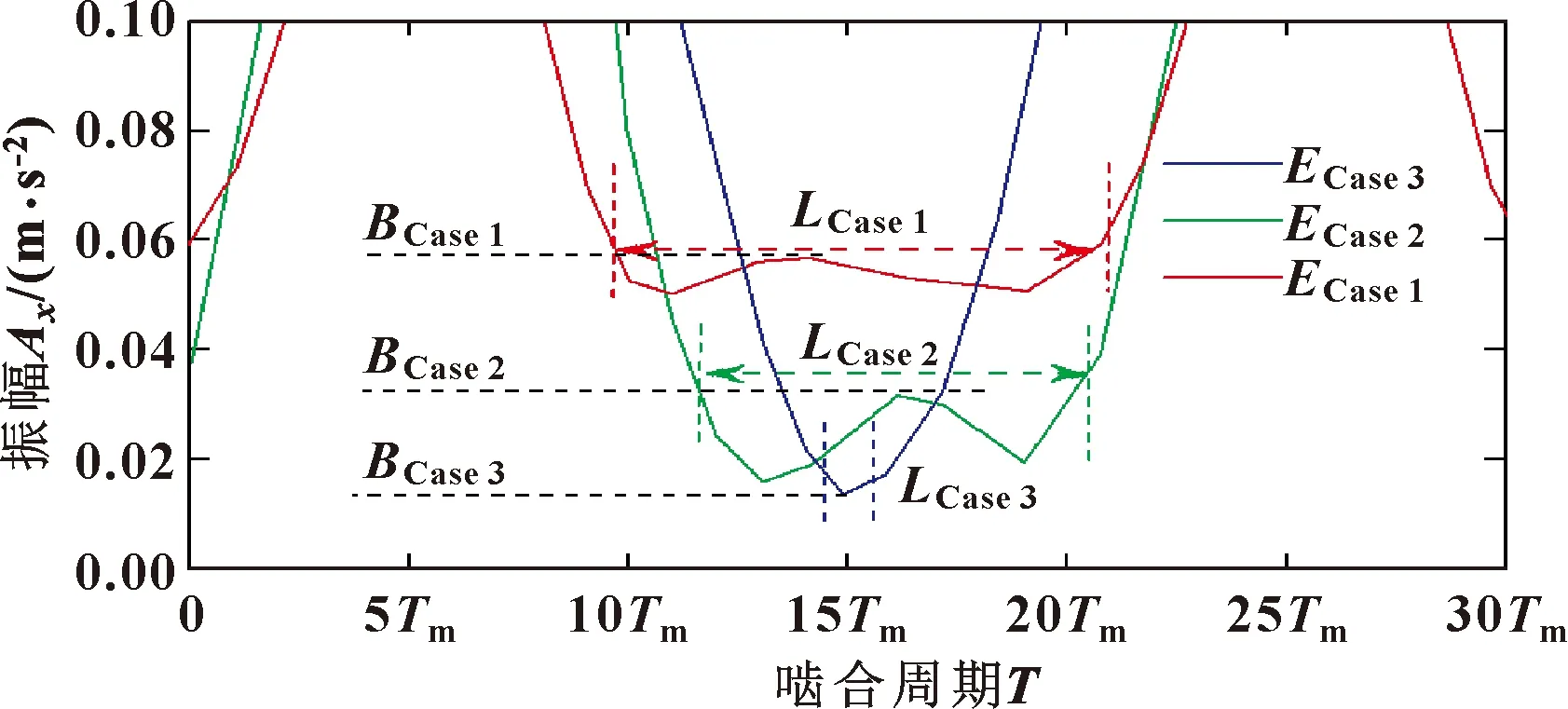
图17 不同螺栓约束下重叠区域的比较
通过以上分析可以看出,螺栓约束对振动信号的幅值调制和重叠具有不可忽视的影响。因此,对于齿轮箱的设计者来说,增加螺栓的数量可以有效地降低齿轮箱的振动幅度,从而提高传动系统的运动精度和使用寿命。
4 实验验证
此研究通过2个实验验证了所提出的加速度信号模型的有效性,实验装置及齿轮箱基本参数如图18和表1所示,传感器安装在齿圈的顶部,变速箱的输入速度为420 r/min。在第一次实验中,螺栓的约束状态对应Case 1。齿轮箱实测实验振动信号如图19所示,横坐标为啮合周期,图中振动曲线显示出明显的冲击特性,主要是由齿轮副的啮合引起的。

图18 行星变速箱试验装置
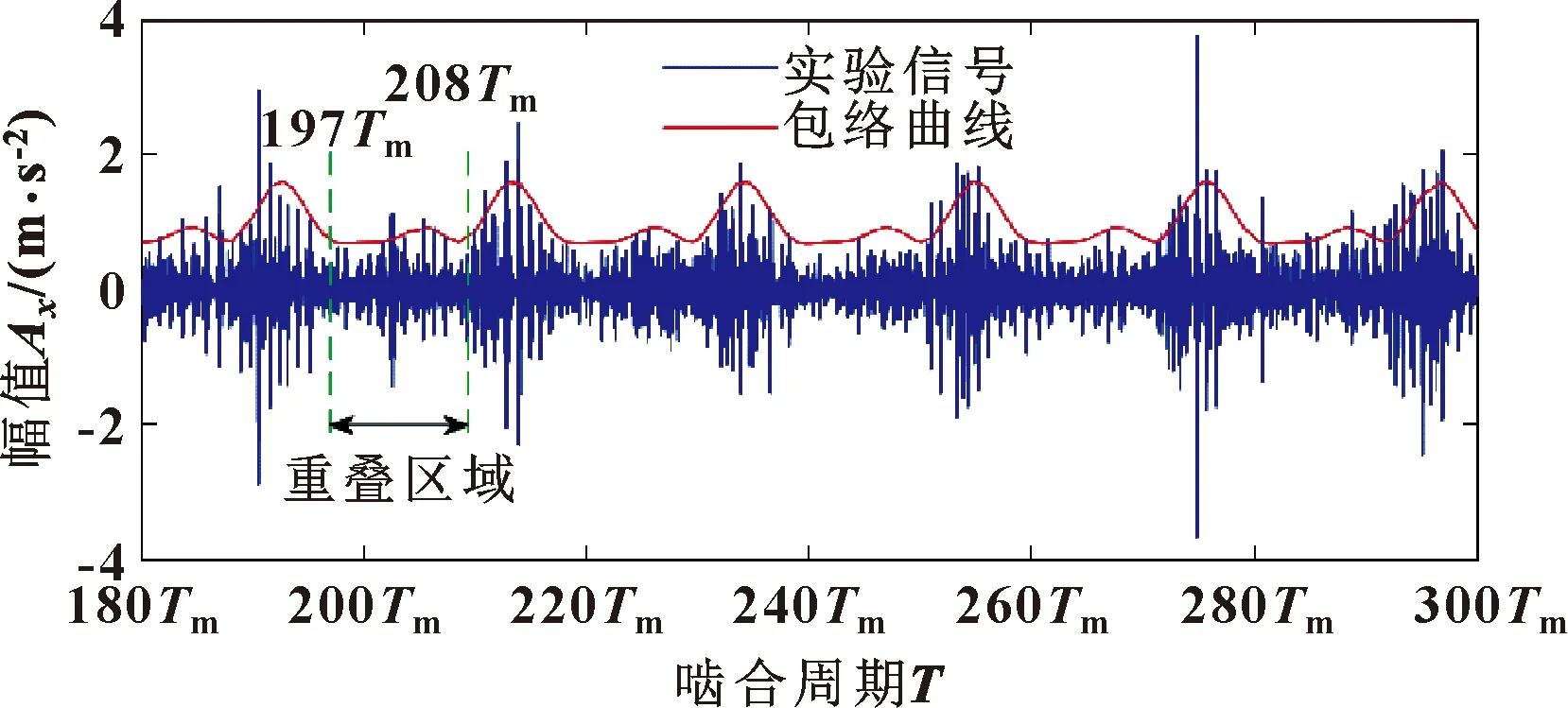
图19 螺栓约束处于Case 1时实验振动信号和包络曲线
此外,振动信号表明在一个行星架旋转周期Tc中出现3个调幅波动,且波动之间存在重叠区域。红色曲线表示振动信号的包络线,包络曲线的形状与图8中考虑螺栓约束的振动信号的包络曲线相似。重叠区域的长度约为11×Tm,与表4中的理论分析结果一致。由此可以得出结论:图8中的模拟信号与图19中的实验信号是一致的。
齿轮箱振动信号的包络阶谱如图20所示,由于齿轮箱的制造、安装等一些因素,在频谱中出现了大量的干扰成分。除低频区段的阶数外,主要的频率分量主要集中在啮合阶数及其谐波上。图中分别显示了低阶和围绕啮合顺序的部分放大图,低阶区域的阶谱表明,振动信号的主调制阶分别是行星架旋转阶的3倍和6倍。从部分放大图可以看出:对应啮合阶次(Zr=62)的幅值较低,而在第60阶和63阶的幅值较大。通过对振动信号在时频域的分析,可以看出:实验结果与图9中的仿真结果是一致的,结果表明此研究所建立的加速度信号模型在时域和频域上是合理的。
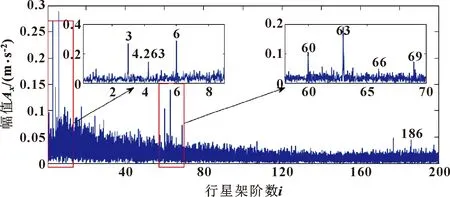
图20 振动信号的包络谱
为了进一步研究螺栓对振动信号的影响,在不停止齿轮系统的情况下,通过拆除齿圈2个螺栓(螺栓1和螺栓8),直接将螺栓约束状态从Case 1改变为Case 3,振动加速度信号及其包络曲线如图21所示。与图18中案例1的结果相比,包络曲线的波动变得平缓,振动幅值变大。这是由于2个螺栓是去除,释放先前抑制的振动信号。另外,拆下螺栓后,变速箱的工作状态发生了变化,振动信号中出现高幅值的啮合冲击。对于重叠区域,Case 3的长度比Case 1短。根据表4中的理论分析,Case 3对应的重叠区域的长度为1×Tm,因此图中重叠区域的长度不明显。实验结果证明了改变螺栓数模拟结果的正确性。
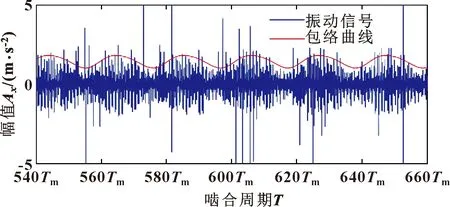
图21 螺栓约束处于Case 3时实验振动信号和包络曲线
5 结论
基于集总参数模型和欧拉-伯努利梁理论,建立了考虑齿圈螺栓约束的行星齿轮箱振动信号模型。基于该模型,研究了振动信号的传递机制、振幅调制和重叠现象以及螺栓约束对信号的影响。主要结论如下:
(1)由于齿轮箱中各部件之间的相互作用,当一个部件发生改变时,其他部件也受到影响。由于传感器靠近齿圈,选择齿圈的振动研究齿轮箱的振动机制合理。
(2)基于集总参数模型,求解了各部件的振动位移,计算了内齿轮副的啮合力,然后将带螺栓约束的齿圈简化为欧拉-伯努利梁,通过求解梁的振动建立齿圈上任意点的振动信号。仿真结果表明:螺栓对振动信号有明显的抑制作用,仿真信号与真实传感器信号具有较高的相似性。
(3)与传统的基于集总参数模型的方法相比,该模型考虑了传感器安装位置和齿圈螺栓约束的数量对振动信号的影响,结果表明这2个因素对信号的幅度调制和重叠现象有本质的影响。
