以问题为驱动 以说理为指导——小学数学问题驱动教学的思考与实践

☉赵文婷

在新课程背景下，传统的数学教学已经无法满足当代学生的学习需求了。所以说，在实际的数学教学过程中，教师应该专注问题驱动教学，以问题为导向，营造出问题驱动的氛围，有效调动学生的学习思维，让他们能够展开自主学习及探究学习，进而实现以问题为驱动、以说理为指导的教学效果，彻底启发学生的数学思维，培养他们开放、自主、探究的能动性，以此提升学生的数学核心素养，让他们获得更为深远的发展。

一、内涵辨析：从“教师推动”走向“问题驱动”

纵观人类的教育史，从孔子的“启发式教学”到苏格拉底的“产婆术”可以得知：他们都将设置问题当成了最重要的教学策略之一。而问题也被称之为一种最有影响力的教学行为。教师在实施课程教学时，应当以问题来推动课程教学，将教师推动走向问题推动，让学习真正的生动、形象与可为［1］。

以苏教版小学六年级数学课本教材为例，教师在教学《分数乘法》时，就应该专注于由问题驱动来实施教学。对此，教师就应该站在分数乘法的角度，为学生设计一个驱动式的问题。如，1／3×2 ＝1／6。很明显，这是一个错误的算式。但是如果教师将其当作是驱动性的问题，就能够让学生充分调动自己的能动性。他们会感觉特别的疑惑，会尝试以各种方式去证明1／3×2 ＝2／3，而不是1／36。他们在学习探究的过程中，其实能够对分数的乘法内涵展开探究与辨析，最终在对这一问题展开探究证明与分析的过程中，便能够完成对这一系列知识的有效建构。他们会站在“学什么”的角度上去思考“怎么学”这一问题。而教师通过问题驱动，也能够帮助学生去深刻理解教学知识内容的本质，能够以学生的认知为起点，驱动他们去展开自主学习，让真正的学习行为得到发生，彰显整个教学的核心，以此凸显学生的综合性学习效能。

二、基本策略：从“关注知识”走向“聚焦素养”

由问题来驱动教学，是需要遵循辩证性、完备性及适用性的基本原则。对此，教师就应该依据学科的特点及儿童认知的特征，以基本的策略为导向来实施驱动教学，从关注知识走向聚焦素养，充分凸显整个教学的核心力及内驱力。首先，教师要以目标来统领整个教学活动。其次，教师应该创设多元化的活动来引导学生展开探究实践，引导学生经历知识“数学化”及“再创造”的过程，让学生能够将实际问题抽象出数学知识，经历对这些知识再创造及再创新的过程［2］。最后，教师应该专注于意识的渗透。

以苏教版小学六年级数学课本教材为例，教师在进行《长方体与正方体的表面积》一课的教学时，就应该注重学生素养的提升与深化。首先，教师应该根据本节课的知识内容确定教学的三维目标。其次，教师应该创设多元化的教学活动，让学生经历知识再创造与再创新的过程。对此，教师可以设计以下教学过程，融合多元化的教学活动，激活学生的主动性思维。教学框架如表1。

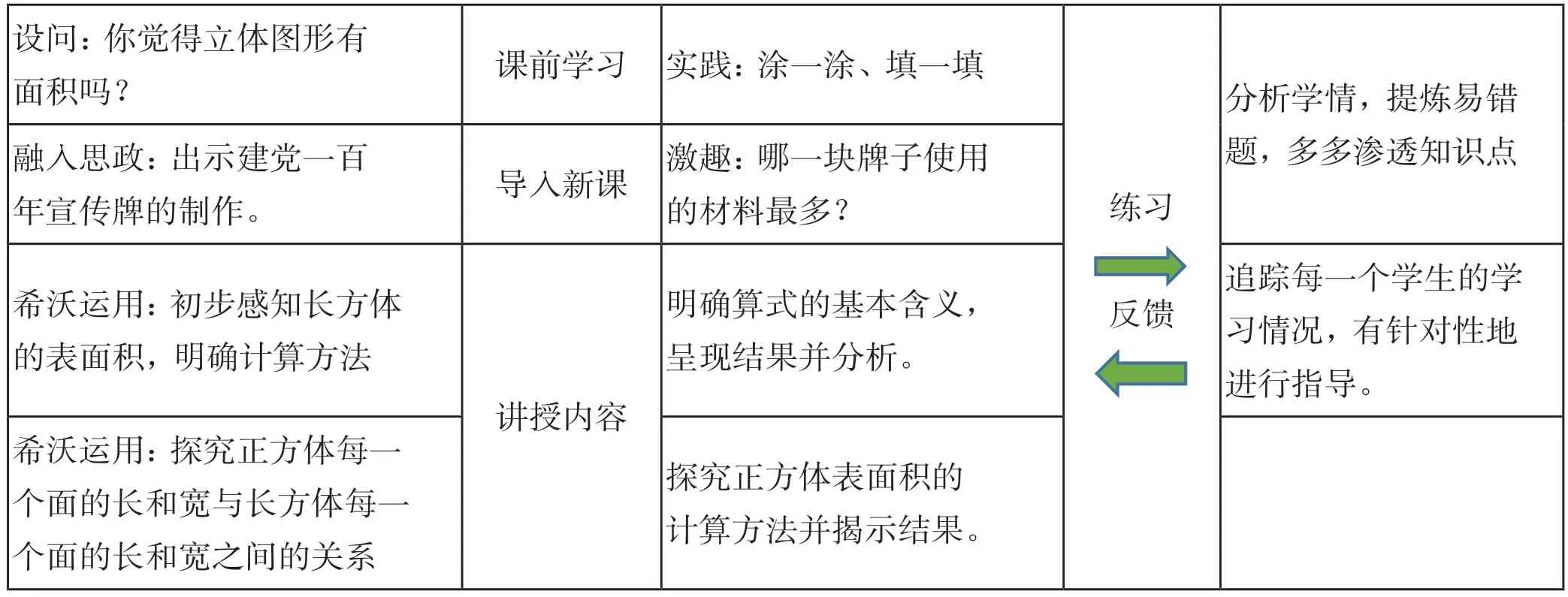
表1 多元化教学活动过程表

最后，教师应该注重意识方面的渗透，要对学生的学习能力及思维品质展开多元化的渗透。例如，在让学生探究知识的过程中激活他们的学习潜能，彰显他们的自主性及探究性。

三、案例剖析：从“环环相扣”走向“板块推进”

在实施课程教学的过程中，教师可以尝试以案例剖析来实施问题驱动教学，按照“抓大放小”“以大带小”的方式，给予学生更多的探究与实践的空间，彰显他们的能动性及主动性，从环环相扣走向板块推进，借此激活学生的学习探究兴致。

以苏教版小学六年级数学课本教材为例，教师在教学《分数除法》时，就应该紧扣教学核心来实施案例教学。如，设计以下两个板块：

板块一：探索算法，理解算理

教师可以先出示一道计算题，如：“2÷2/3”，让学生进行试算、演算以及分析每一步的含义。例如，教师可以让学生将2÷2/3 展开多元化变式训练：

变式一：2÷2/3 ＝（6×1/3）÷（2×1/3），以此来分析“（6×1/3）÷（2×1/3）”所代表的算理便是“6 个1/3 是2 个1/3 的几倍”。

变式二：2÷2/3 ＝（2×3）÷（2/3×3），以此来分析“（2×3）÷（2/3×3）”所代表的算理便是“商不变的规律”。

变式三：

2（×3/2）对应2/3（×3/2）份

？ 对应 1 份

如上，教师通过这样的方式，让学生展开了多元化的变式训练，让学生探索分数除法的算法，理解算理，从整数除法迁移至分数除法层面，实现了知识之间的迁移运用，以此也实现了学生的高质量学习。

板块二：巩固算法，归纳要领

在这一板块的教学中，教师可以为学生出示实际应用题，让学生进行计算，归纳要领，巩固分数除法的基本算法。案例如下：

小明妈妈从超市买了4/5 千克的香蕉，共花费25 元，1/5 千克的橙子，花费43 元，3/4 千克的西瓜，花费56 元。已知这些水果的总重量为24 千克，请问每一种水果的单价是多少呢？

如上，这是一道较为复杂的计算题，它需要学生展开多个步骤的计算，最终才能够得出每一种水果的单价。所以说，教师以板块为基准点，以层层递进的方式去驱动学生展开学习实践，能够让学生有更强的自主学习权利，充分彰显他们在学习过程中的主观能动性。

四、教学设计：从“撰写教案”走向“教学规划”

教学设计是实施课程教学的前提和基础。教师在展开教学设计时，应该充分考虑到学生、教师的教学以及教师自身等基本元素，并且要将这些元素相互融合、相互联系，形成一个有机的整体，将其变成富有生机的教学活动系统。所以，由问题驱动实施的教学，能够让教师从传统的教案撰写走向科学的教学规划，着力于追求“学程设计”“弹性设计”及“动态设计”的和谐与统一，提升学生的综合学习实效。对此，教师就应该以问题为导向来分析基本的教学设计架构，具体如表2。

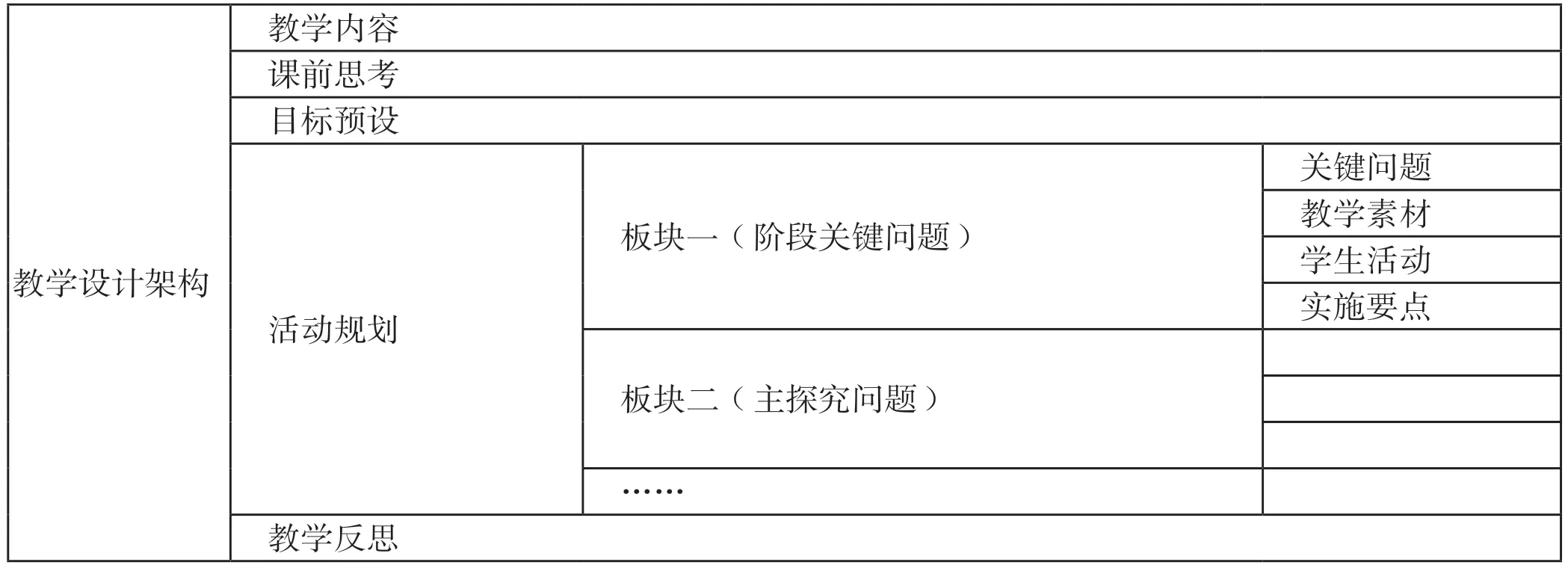
表2 以问题为导向的教学设计架构表

文章以苏教版小学六年级课本教材中的《圆柱体表面积》为例，探究教学设计的架构，具体如下：

教学内容为探寻圆柱体表面积的相关知识内容，明确圆柱体侧面积和表面积的计算方法，并且能够运用这一知识去解决现实生活中的实际问题，参与并经历圆柱体侧面积和表面积公式推导的过程，获得有关于侧面积和表面积的计算方法。在这一过程中，学生能够理解圆柱体侧面展开得到长方形的长与圆柱底面周长的关系以及宽（高）与圆柱高之间的对应关系。

课前思考为教师对整个教学设计的认知背景、学生的学习需要、学生需要学习的内容、展开的活动、学生的心理及认知规律等方面作出科学的规划和分析。例如，学生在此之前已经学习了正方体和长方体的表面积计算，具有一定的基础，那么，教师就可以通过这一方面的思考来预设学生的学习探究活动，让整个教学更加具有针对性，实现学生对所学知识的迁移运用。

目标预设主要是强调整个教学目标的陈述方式，不仅要体现教师的主导作用，还要彰显学生的主体作用，要让整个目标更加富有层次性。目标的结果要通过学生的努力来加以实现，且在这一过程中，教师要赋予可行性的评价标准来彰显学生的学习成果及价值。

活动规划是教学设计的主体部分，也是整个问题驱动教学与一般教学设计的主要分水岭。由问题来驱动教学，需要设计主探究问题以及次要探究问题。且各个关键问题之间能够形成一种板块化的教学结构，要以板块化的教学来推动学生展开科学的学习与实践。在这一过程中，教师应该明白的是：每一个活动板块是需要由阶段性的关键问题、教学素材、学生活动及实施要点等四个部分组成。阶段性的关键问题属于整个教学的主要问题，它统领整个阶段的教学任务。例如，教师把“圆柱体的表面积与长方体的表面积计算方式有什么区别？”“圆柱体的表面积计算公式推导应该从哪里寻求突破点呢？”当作关键性问题，以此驱动学生展开探究与实践。教学素材则是辅助学生去解决整个问题的相关资料［3］。例如，学生学习探究过程中的长方体表面积公式推导步骤、圆柱体解说的相关微课等。学生活动则是明晰学生多元化的学习活动，让学生在学习活动中运用教学材料来解决整个阶段性的关键问题。实施要点是需要教师明确学生在整个学习探究过程中需要注意的事项，以此为基准点来实施板块化的教学设计，很好地引领教师由简单的教案撰写走向对整个教学的深度思考。由此，教学也更加灵活，能够促进教学的个性化及班本化实施，最终彰显学生的综合学习实效。

教学反思主要是记录教师和学生在教学及学习过程中的个人感受和体会。它有助于学生进一步展开学习探究与实践，也能够让教师完善并修改教学计划，助推良好教学效果的生发。

综上所述，在小学阶段的数学教学过程中，教师应该以问题来驱动教学，以“问”促“教”、以“理”导“学”，让整个数学教学充满“问”与“理”的艺术魅力，助推生成性、个性化教学的实现，让整个教学实现多元化的建构，助推学生数学核心素养的发展。