考虑主环境因素的GWO-SVR 风电功率超短期预测

徐炜君

（东北石油大学秦皇岛校区电气信息工程系，河北秦皇岛 066004）

随着“碳达峰碳中和”目标的提出，可再生能源的作用愈显突出，我国可再生能源装机规模持续扩大，截止到2021 年11 月底，我国风电装机容量已跃居世界首位，约为3 亿千瓦，同比增长29%，风电利用率达到了96.9%。但风自身的不稳定性，使得风力发电具有波动性、间歇性和非线性的特点，因而大规模的风电并网会对电网调峰、调频和安全稳定运行带来极大挑战[1]。为了更加合理地利用风电，提高风电功率预测精度成为学界研究的热点。

目前，国内外学者已经提出了许多成熟的风电功率预测方法，这些方法主要分为两类：物理方法和统计方法。物理方法根据数值天气预报和风机组自身信息以及周围的物理信息构建出的物理模型进行预测[1]。统计方法主要是利用机器学习方法，诸如BP(Back Propagation)神经网络、K 邻近算法(K-Nearest Neighbor，KNN)、随机森林（Random Forest，RF）、支持向量机（Support Vector Machine，SVM）、极限学习机（Extreme Learning Machine，ELM）等，对大量的风速、风向、温度、气压等数据进行训练和回归预测，进而实现风电功率预测[2-4]，并且输入数据维度越高，更有利于探索其动态变化规律[5]，但输入数据维度越高，预测模型的复杂程度越大，预测的时间会增加，这不利于风电的超短期预测。

为此，文中在深入分析影响风机出力的主要环境因素的基础上，对风电场的采样数据进行了降维处理，并用GWO-SVR 预测模型进行预测分析，实验结果对比表明，经过降维处理后，有效地降低了预测模型的复杂程度，降低了无用数据对预测结果的影响，GWO-SVR 预测算法在稳定性、预测时间及精度三个方面均有提高。

1 影响风机出力的主要因素分析

根据空气动力学和贝兹准则可知，风机从风能中捕获的功率可表示为[6]：

其中,P为风机的输出功率，Cp(λ,β) 为叶片的风能利用系数，λ为叶尖速比；β为桨距角，A为风轮扫掠面积，单位为m2，ρ为空气密度，单位为kg/m3，v为风速，单位为m/s。

1.1 风能利用系数对风机出力的影响

叶尖速比可表示为：

其中，ωm为风轮角速度，单位为rad/s；R为风轮半径，单位为m，v为风速，单位为

叶片风能利用系数的一种解析计算方法为[7]：

综合式（2）-（4）可知，风能利用系数为角速度ωm、桨距角β和风速v的相关函数，可记为：

叶尖速比λ由风速与风轮转速决定，而当叶片一定时，叶片最佳桨距角β一定，因此对于一个风机来说，其风能利用系数仅与风速和风轮转速有关，对于特定的风速，存在唯一的转速使得Cp达到最大。而单从风电预测考虑，只要能够准确预测出风速，通过对风机转速的系统控制，就能够得到Cp的最大值[8]。因此，单从风电预测考虑，风能利用系数主要与风速有关。

1.2 风轮扫掠面积对风机出力的影响

风轮扫掠面积是与风向垂直的平面上，风轮旋转时叶尖运动所生成圆的投影面积，具体计算为：

其中，R为风轮半径，单位为m，α为风向的垂直平面与风轮旋转圆平面之间的夹角，0°≤α≤90°，由式（6）可以看出，风向是影响风机出力的主要因素之一。

1.3 空气密度对风机出力的影响

由式（1）可知，风机的输出功率与空气密度成正比，而影响空气密度的环境因素有气压、温度、海拔高度和湿度[9]。根据风电场所处的不同地理环境，有些影响空气密度的环境因素不需考虑，比如已经建设好的风电场，其海拔高度不变，因此可以不考虑海拔对空气密度的影响。文中所涉及的风电场属于这种情况，以下将分析气压、温度和湿度对空气密度的影响。

空气密度与气压、温度、湿度的关系可以表示为[10]：

其中，ρ为10 min 内的平均空气密度，P为10 min 内测量的干燥空气平均气压，R0为干燥空气的气体系数，取287.05 J/(kg·K)，T为10 min 内的平均测量温度，T=Tc+273.15，Tc为实际温度。Pv的计算如式（8）所示：

其中，C0=6.107 8,C1=7.5,C2=237.3，均为特滕斯公式（Tetens Formula）的系数。PH%为相对湿度，定义为实际水蒸气压力和饱和水蒸气压力的比值。

综合式（7）-（8）可以看出，气压、温度、湿度的变化都会引起空气密度的变化。为了进一步分析其变化规律，分两种情况：

1）湿度一定，气压和温度对空气密度的影响如图1 所示。从图1 可以看出，随着气压降低和温度升高，空气密度会变小。

图1 空气密度与气压、温度的关系

2）气压一定，湿度和温度对空气密度的影响如图2 所示。从图2 可以看出，在气压一定且温度较低时（如-20 ℃），湿度的剧烈变化对空气密度的影响不大；而在高温区域（如+30 ℃左右），随着相对湿度的增加，空气密度会降低。湿度和温度对空气密度影响的整体趋势是：随着相对湿度变大和温度升高，空气密度将会变小。

图2 空气密度与湿度、温度的关系

综上，在一个固定的风电场，温度、气压和湿度的变化会影响空气密度的变化，进而影响风机出力，因此，在进行风电预测时应该考虑温度、气压和湿度三个环境因素的影响。

通过上文分析可以看出，影响风机出力的主要环境因素有温度、湿度、气压、风向和风速，在进行风电预测时，应该重点关注这几个环境因素。

2 风电场数据建模及降维处理

风电场一般由若干台风机组成，各风机的分布需要根据地势、尾流效应及主风向等因素而定，同时由于风能随机波动性的影响，风电场中各风机的出力不能随时与风力相匹配，因此风电场的风电功率预测应从全局出发，应着重考虑整个风电场的风电特性，而风电场中的测风塔最能反映这一特性[11]。目前业界比较认可的风电功率预测有两种方法：一是先预测风速，然后根据风电场的功率曲线得到风电场的输出功率；二是直接预测其输出功率[11]。文中采用第一种方法。

2.1 风电场数据建模

以新疆昌吉州某风电场测风塔的历史监测数据进行数据建模。该风电场的平均海拔高度为967 m，地形以戈壁为主，风机主要为2.2 MW 风机，高度为80 m，测风塔塔高为70 m。测风塔可分别测量70 m、50 m、30 m 和10 m 高处的风速及风向，7 m 高处的气压、温度和湿度，其数据采集以10 min 为间隔，每1 s采集一次数据，并对10 min 的600 个数据进行统计分析，计算出平均值、最大值、最小值和标准差。每一个10 min 间隔可以得到一个44 维的向量。

考虑到风电场当地每年四五月份的气候变化比较剧烈，因此选用2020 年4 月26 日—5 月5 日10 天的日监测数据作为建模数据，每天以10 min 为间隔进行数据采样，最终得到一个1 440×44 的样本集。为了使各维分量在实际的预测过程中具有相同的地位，必须将这些量纲、取值范围各不相同的数据使用归一化方法变换到同一范围，归一化方法为：

其中，i=1,2,…,1 440，j=1,2,…,44，yi(j) 为实际分量，max[yi(j)]、min[yi(j)]分别为第j个分量的最大和最小值，xi(j)为归一化后的分量值，归一化后数据的取值范围均为[-1,1]。

2.2 风电场数据降维处理

如果用2.1 得到的1 440×44 的数据作为预测模型的训练和测试样本集，由于该数据维度较高，会严重影响预测模型的运算速度和精度，因此需要对数据进行降维处理。

通过第1 节的分析可知，风速和风向是影响风机出力的主要因素，因此在数据降维处理时必须考虑这两种因素。风速及风向的最大值和最小值只能反映该时间段内的极值分布，其标准差反映数据的分散程度，而风速及风向的平均值可以反映其在某一个时间段的趋势，同时考虑到影响风机出力的主风速应该和风机高度相当，所以选用70 m 高处的风速及风向的平均值作为建模数据。

风速是地形、海拔、气压、湿度、温度等多种因素共同作用的结果[12]，同时气压、湿度、温度的变化会引起空气密度的变化，进而影响风机出力。假定在相邻的采样周期内（20 min 内），风速和风向不变，风机出力只与空气密度有关，用式（7）和式（8）计算每个采样周期（气压、湿度、温度用平均值）的空气密度，并用式（10）计算相邻采样周期的空气密度变化率：

其中，ρi为第i个采样周期的空气密度，i=1,2,…,1 439，Rρi最大变化率为1%，出现在4 月27日上午9：50-10：00 和10：00-10：10 这两个相邻的采样间隔，十天内变化率大于0.5%的相邻时刻有9 次，说明短时内空气密度也会有大的波动，因此结合该风电场的实际，应将气压、温度和湿度作为建模数据。通过上述降维处理，将原来的44 维数据降为了风速、风向、气压、温度和湿度5 维数据，这样可以极大地提高计算速度。

进一步分析1 440×5 样本数据发现，该样本集中气压的变化最小。将每维1 440 个数据分成240 份，每份6 个数据，对应一个小时的数据，对240 份（小时）数据分别求数据的标准差，得到图3 所示的标准差比较曲线。从图3 可以看出，与其他天气因素比较，在某段时间内气压的标准差几乎不变或者变化非常小，说明其数据比较集中，波动性较小，因此在实际的预测分析中可以不考虑气压的影响，这样可以将1 440×5 样本集进一步降为1 440×4 样本集，进一步提高计算速度，降维过程充分考虑了影响风机出力的主要因素，同时也考虑了风速、风向、温度和湿度之间的相互影响和联系。

图3 气象数据标准差比较曲线

3 GWO-SVR预测模型设计

3.1 支持向量回归机（SVR）

支持向量回归机（SVR）由Vapnik 于1995 年首次提出，其核心思想是通过引入非线性映射φ(x)，实现样本空间从低维到高维的变换，通过在高维空间的线性回归得到原样本的非线性特性[13]，其映射关系表示为：

核函数类型的选取会直接影响回归结果，同时考虑到核函数参数的数量对预测模型复杂程度的影响，文中选择能够实现非线性映射的径向基函数（Radial Basis Function，RBF）作为SVR 的核函数，其表达式为：

其中，σ为待确定的核函数参数。由式（12）、（13）可知,只要选取合适的C、ε、σ便可以确定SVR 的具体形式，从而对控制对象进行准确预测[13]。在实践中发现，ε值的选取独立于C、σ的选取，因此可以根据SVR 的建模精度先确定ε，再优化参数C、σ，这样可以降低参数优化的复杂程度[13]。

3.2 灰狼优化算法

灰狼优化算法(Grey Wolf Optimizer,GWO)是澳大利亚学者Mirjalili 于2014 年受灰狼捕食行为的启发，提出的一种群智能优化算法[14-15]。GWO 算法将狼群分为α、β、δ、ω四种类型：α狼是领导者（最优解），β狼和δ狼协助α狼对狼群的进行管理及捕猎过程中的决策，同时也是α狼的候选者，ω狼主要协助α、β、δ对猎物进行攻击。当狼群包围猎物时，狼群的位置变化由以下数学模型定义：

其中，t为当前迭代，A和C为协同向量，Xp(t)为猎物的位置向量，X(t)为灰狼的当前位置向量。A、C的计算如下：

其中，a在迭代过程中线性递减且递减范围为[2,0]，r1、r2是[0,1]范围内的随机向量。

根据狼的狩猎行为，将前三个最优值保存为α、β和δ，然后灰狼种群的位置更新公式如下：

其中，Dα、Dβ、Dδ分别表示α、β和δ狼和其他狼之间的距离，Xα、Xβ、Xδ分别是α、β和δ狼的当前位置，C1、C2、C3是随机向量，X是当前灰狼的位置。式（17）、（18）通过a值的递减来实现迭代，最终可得最优解。

3.3 GWO-SVR预测模型的构建

GWO-SVR 预测模型的构建流程如图4 所示，主要步骤为：

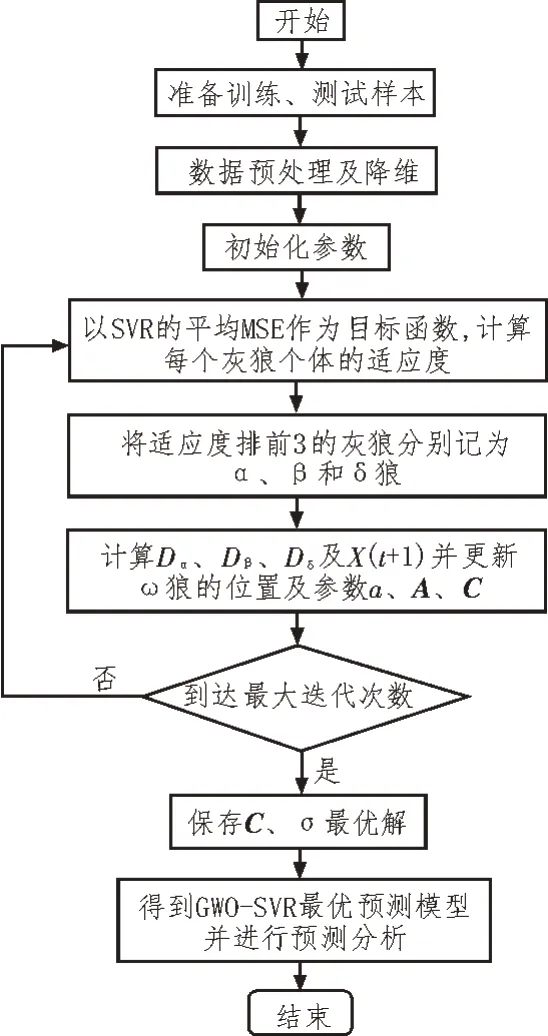
图4 GWO-SVR预测模型流程图

1）取前9 天的数据（4 月27 日-5 月4 日）作为训练样本，第10 天（5 月5 日）的数据作为测试样本，并对训练和测试数据进行预处理和降维。

2）初始化参数：狼群数量为20，最大迭代次数为100，参数C、σ的上下界均为[0.01,100]，α、β和δ狼的初始位置均为(0,0)。

3）以SVR 的平均均方误差MSE 作为目标函数，计算每个灰狼个体的适应度，并将适应度排前3 的灰狼位置记为Xα、Xβ、Xδ。

4）依据式（17）、（18）计算Dα、Dβ、Dδ及X(t+1)，并更新ω狼的位置及参数a、A、C。

5）判断是否到达最大迭代次数，如达到则保存C、σ最优解，否则返回步骤3）。

6）得到GWO-SVR 最优预测模型并进行预测分析。

4 实验仿真与分析

以3.2 节得到的样本集为例，进行仿真与分析。为了验证经过降维处理后，可以提高预测的精度及速度，分别建立GA-SVR、PSO-SVR、GWO-SVR 三种预测模型，并对不同维度的样本集用这三个模型分别进行预测分析，采用均方根误差(RMSE)及衡量拟合度的复测定系数R2作为预测模型的评价指标[16-18]。

采用以下六种不同维度的样本集作为训练和测试集，分别用GA-SVR、PSO-SVR、GWO-SVR 三种预测模型预测70 m 处的平均风速，得到的预测结果如表1 所示。

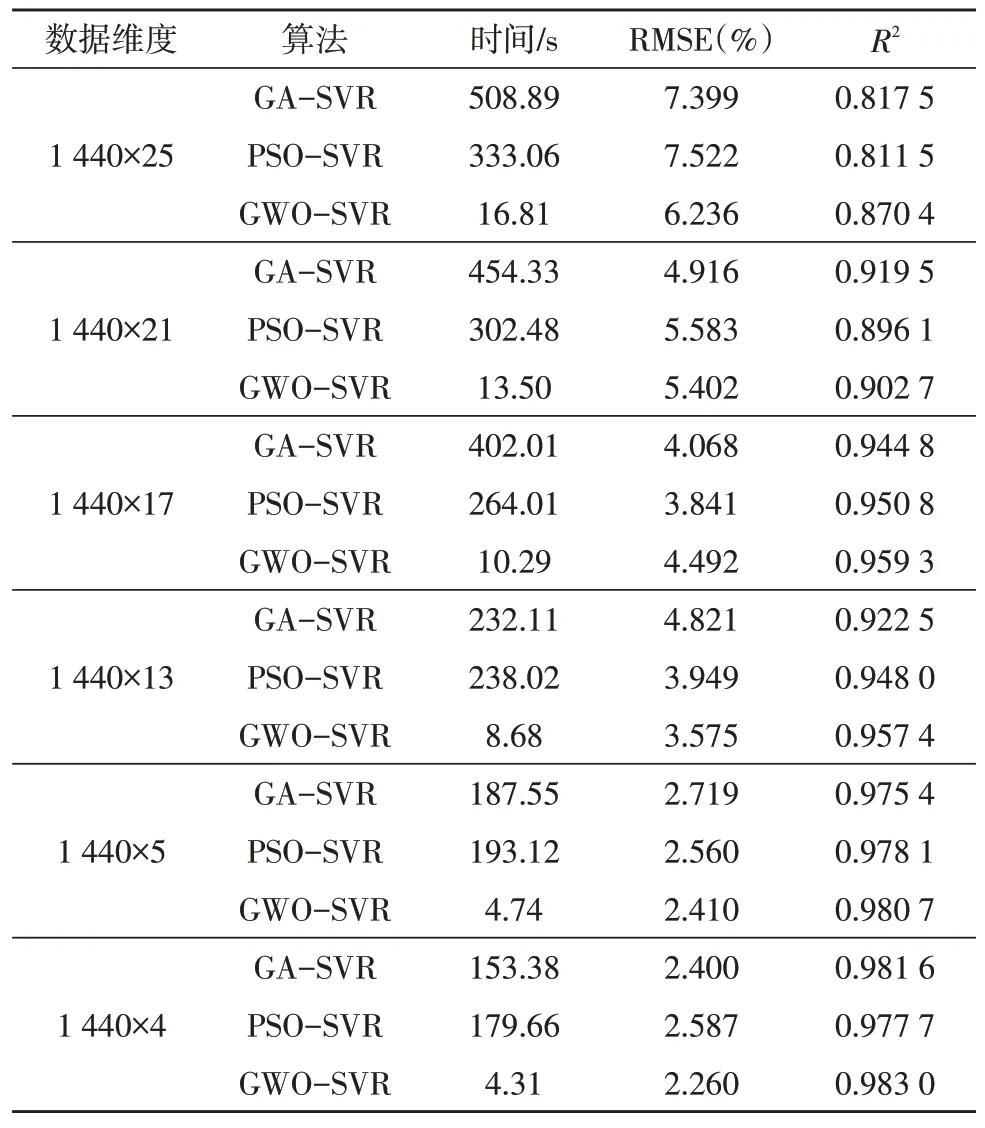
表1 不同算法在不同数据维度下预测结果

1）1 440×25：70 m、50 m、30 m、10 m 处风速及7 m处气压、温度、湿度的平均、最大和最小值，70 m、50 m、30 m、10 m 处风向的平均值。

2）1 440×21：70 m、50 m、30 m 处风速及7 m 处气压、温度、湿度的平均、最大和最小值，70 m、50 m、30 m 处风向的平均值。

3）1 440×17：70 m、50 m 处风速及7 m 处气压、温度、湿度的平均、最大和最小值，70 m、50 m 处风向的平均值。

4）1 440×13：70 m 处风速及7 m 处气压、温度、湿度的平均、最大和最小值，70 m 处风向的平均值。

5）1 440×5：70 m 处风速及7 m 处气压、温度、湿度的平均值，70 米处风向的平均值。

6）1 440×4：70 m 处风速、风向及7 m 处温度、湿度的平均值。

从表1 可以看出，随着数据维度的降低，三种算法的预测时间都在减少，预测能力也逐渐增强（RMSE 逐渐减小），拟合度也越来越好（R2逐渐变大）。但是这三种算法的预测能力存在较为显著的差别，图5、6、7 分别为各算法的预测时间、RMSE 及R2的比较曲线。图8 为三种算法在1 440×4 维度下预测的70 m 处平均风速的比较曲线。

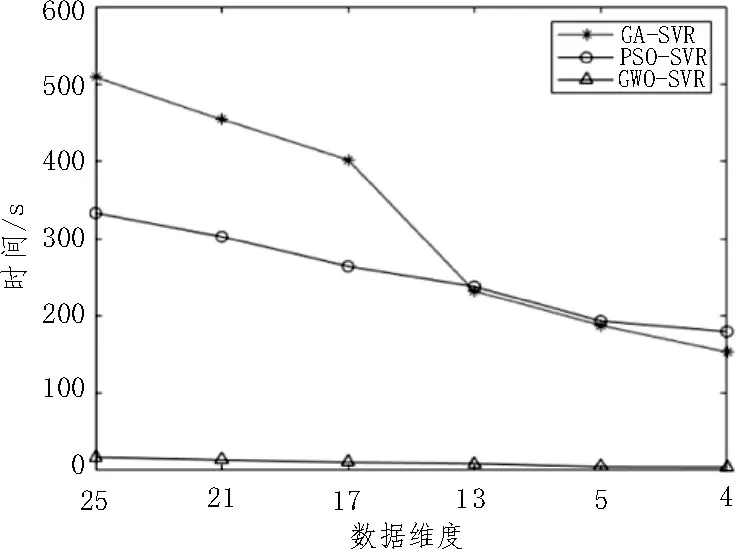
图5 不同算法预测时间比较

图6 不同算法RMSE比较

图7 不同算法R2 比较

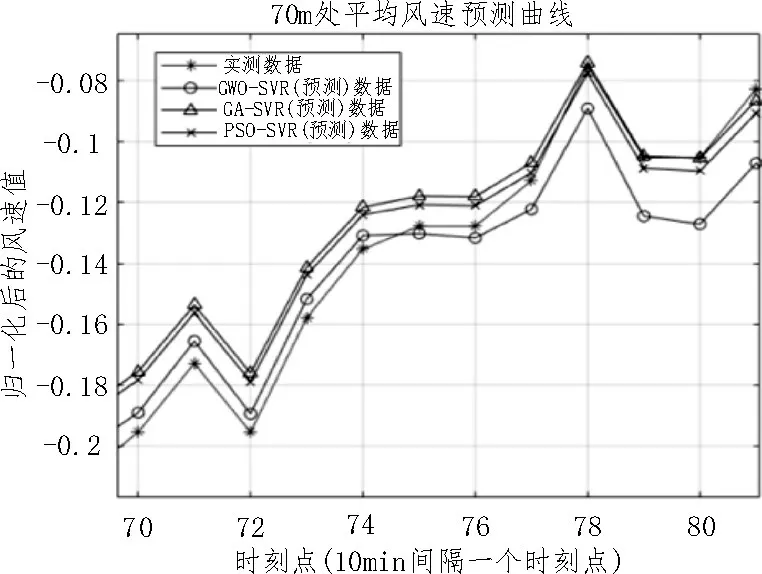
图8 风速预测比较曲线（局部）

从图5 可以看出，数据维度较高时（1 440×17 以上），GA-SVR 的预测时间接近PSO-SVR 的1.5 倍，在低维（1 440×13 以下）时两者的预测时间相当，GWO-SVR 的是三种算法预测时间最短的，在高维时为PSO-SVR 的5%左右，在低维时为PSO-SVR 的2.5%左右。

从图6 可以看出，三种算法的均方根误差(RMSE)随着数据维度的减少都在减小，但是在高低维过渡时GA-SVR 和PSO-SVR 算法的RMSE 存在波动，而GWO-SVR 算法为单调递减。

从图7 可以看出，三种算法的R2在高低维过渡时均有波动，但是GWO-SVR 算法的波动最小，并且其拟合度在低维时是三者中最好的。

通过上述比较分析可以可出，经过降维处理后GWO-SVR 预测算法在稳定性、速度及精度三个方面均有提高。

5 结论

为了更加合理地利用风电，减少风电并网对电网调峰、调频和安全稳定运行的影响，文中在深入分析影响风机出力的主要环境因素的基础上，以新疆某风电场为例，对其测风塔采集的高维环境监测历史数据进行了降维处理，并在此基础上采用GWOSVR 预测模型对该风电场的风速数据进行了预测分析，并和GA-SVR、PSO-SVR 算法进行了比较。实验结果表明，经过降维处理后，GWO-SVR 预测算法在稳定性、速度及精度三个方面均表现了优异的性能。