空气密度年变化情况对风电场发电量计算的影响
2023-05-06吴天太
吴天太
(中国三峡新能源(集团)股份有限公司甘肃分公司,兰州 730000)
0 引言
目前市场主流的风电场发电量计算软件WT、WAsP 等均采用年平均空气密度作为发电量计算时的空气密度,然而这种用年平均值替代每时每刻瞬时值的方法,未考虑空气密度的年变化情况对风电场发电量计算的影响,因此一些相关的风电场发电量计算软件开发商在考虑是否有必要使用空气密度时间序列来计算风电场发电量[1]。
基于此,本文主要分析空气密度年变化情况对风电场发电量计算的影响,旨在评估空气密度年变化情况引起的风电场发电量计算误差,考虑使用空气密度时间序列计算风电场发电量的必要性。首先对中国空气密度的年变化幅度的大致情况进行分析;然后选取10 座有代表性的测风塔,对其所在区域的空气密度年变化情况进行统计分析,探究空气密度的区域年变化情况,并分析空气密度的主要影响因素;最后选取其中空气密度年变化幅度较大的1 座测风塔数据来分析空气密度年变化情况对风电场发电量计算的影响。
由于风速的年变化情况和空气密度的年变化情况没有固定的函数,很难从理论公式上推导空气密度年变化情况对风电场发电量的影响,因此,本文以某型号风电机组的单机理论发电量计算为例来分析空气密度年变化情况对风电场发电量计算的影响。
1 中国空气密度年变化幅度的大致情况
为探讨空气密度年变化情况对风电场发电量计算的影响,必须分析中国空气密度年变化的幅度,以此来分析各区域空气密度年变化情况对风电场发电量影响的大小,同时探究空气密度的主要影响因素。
1.1 空气密度的计算公式[2]
空气密度的计算公式可表示为:
式中:ρ为空气密度,kg/m3;P为年平均大气压力,Pa;T为年平均开氏温标空气温度,K,T=273.15+t(其中t为摄氏温度);R为气象常数,J/(kg·K),取287。
从式(1)可以看出,空气密度和年平均大气压力成正比,和年平均开氏温标空气温度成反比。
1.2 中国代表性区域的空气密度年变化情况分析
在中国范围内各种地形和气候条件下,选取最具代表性的10 座测风塔,统计分析这些测风塔所在10 个区域的空气密度年变化情况[3]。选取的10 座测风塔分别位于云南省楚雄州(下文简称为“云南楚雄”)、福建省莆田市(下文简称为“福建莆田”)、陕西省渭南市(下文简称为“陕西渭南”)、新疆维吾尔自治区乌鲁木齐市(下文简称为“新疆乌鲁木齐”)、黑龙江省同江市(下文简称为“黑龙江同江”)、内蒙古自治区乌兰察布市(下文简称为“内蒙古乌兰察布”)、青海省海西州(下文简称为“青海海西”)、江苏省扬州市(下文简称为“江苏扬州”)、广东省清远市(下文简称为“广东清远”)、湖北省宜城市(下文简称为“湖北宜城”),分析每座测风塔某1 个完整年的数据。
各代表区域测风塔某1 个完整年的空气密度、空气温度、大气压力的月平均值及年变化情况分别如表1~表3 所示。表中,年平均值采用10 min 时间序列计算得到。各代表区域的空气密度的年变化幅度如图1 所示。
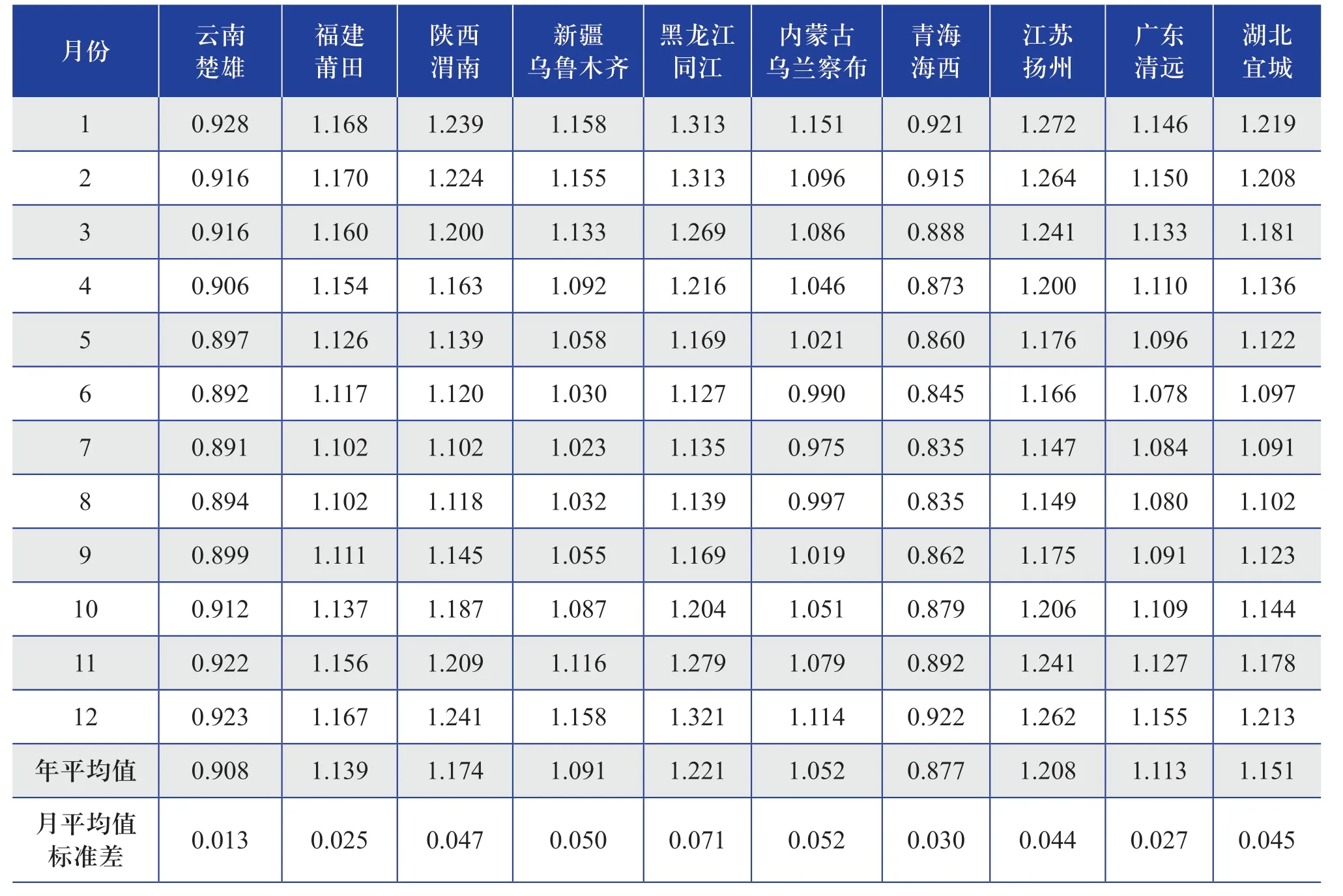
表1 各代表区域测风塔某1 个完整年的空气密度的月平均值及年变化情况Table 1 Monthly average value and annual variation of air density in a complete year of anemometer tower in each representative region(单位:kg/m3)
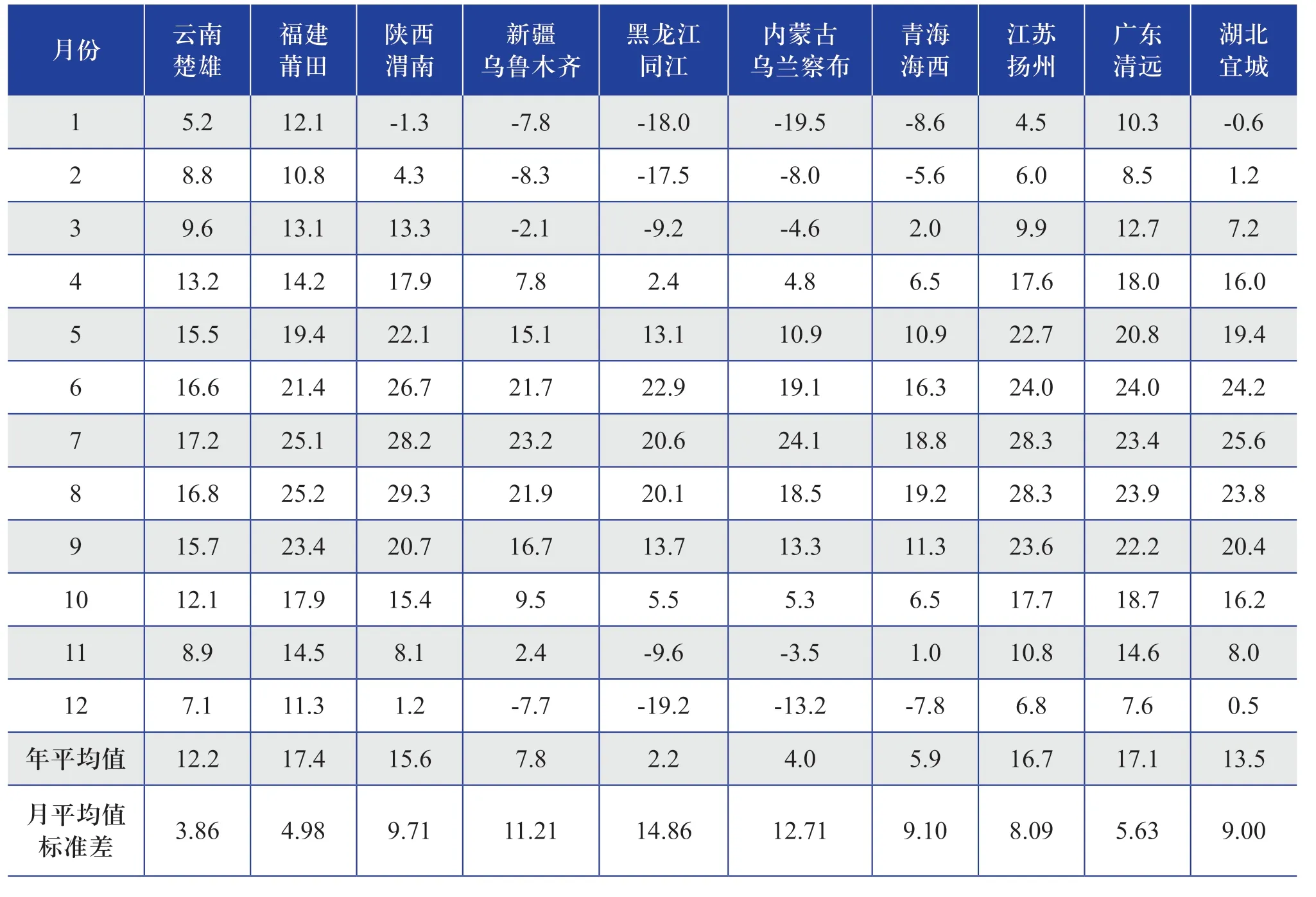
表2 各代表区域测风塔某1 个完整年的空气温度的月平均值及年变化情况Table 2 Monthly average value and annual variation of air temperature in a complete year of anemometer tower in each representative region(单位:℃)
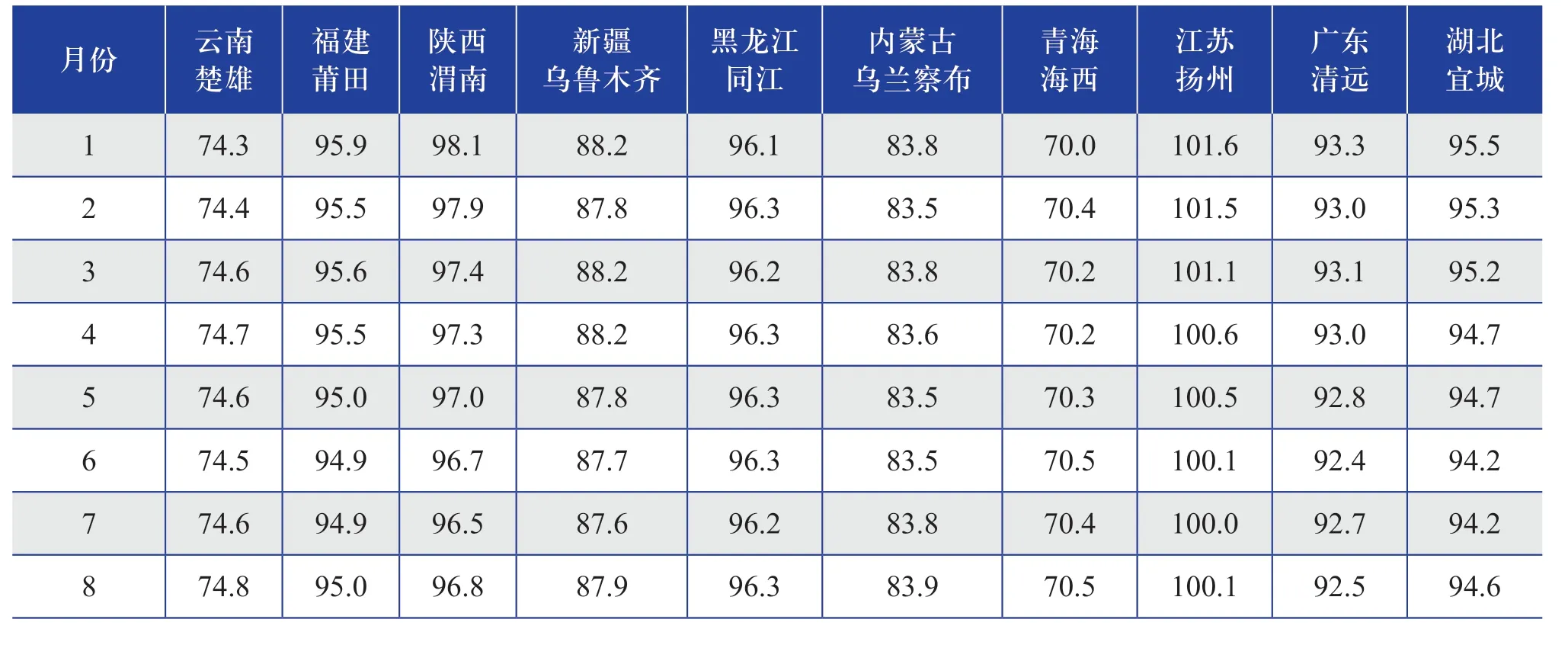
表3 各代表区域测风塔某1 个完整年的大气压力的月平均值及年变化情况Table 3 Monthly average value and annual variation of atmospheric pressure in a complete year of anemometer tower in each representative region(单位:kPa)
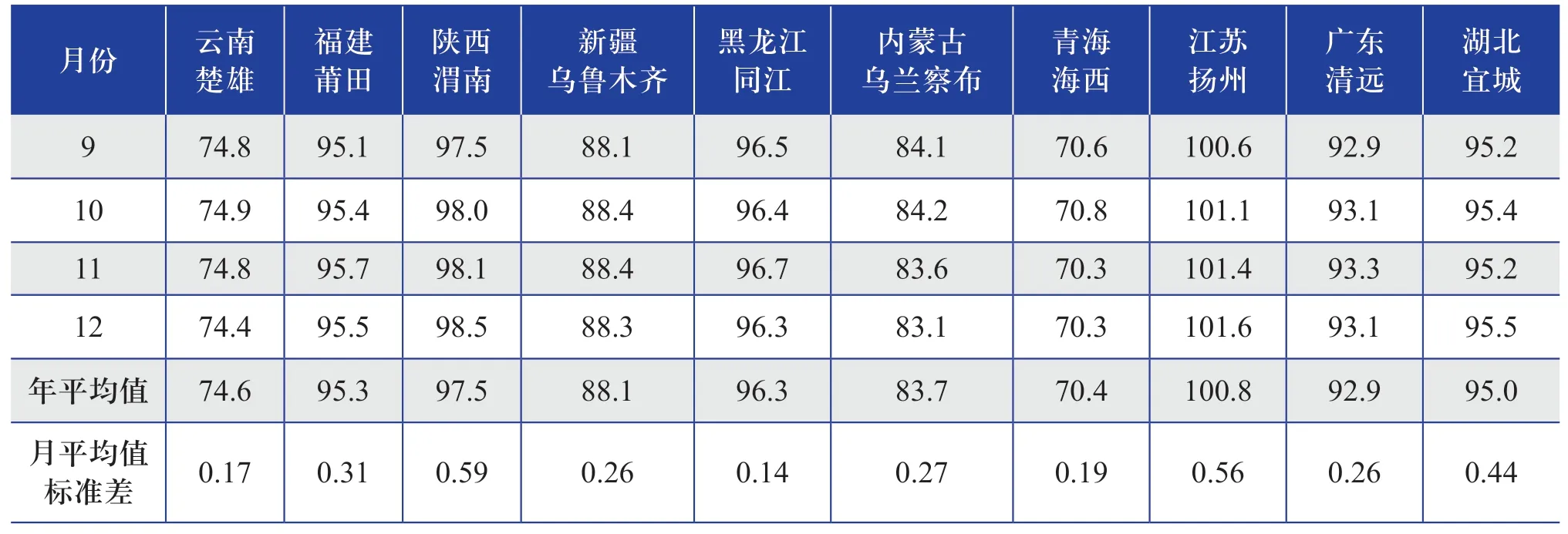
(续表)
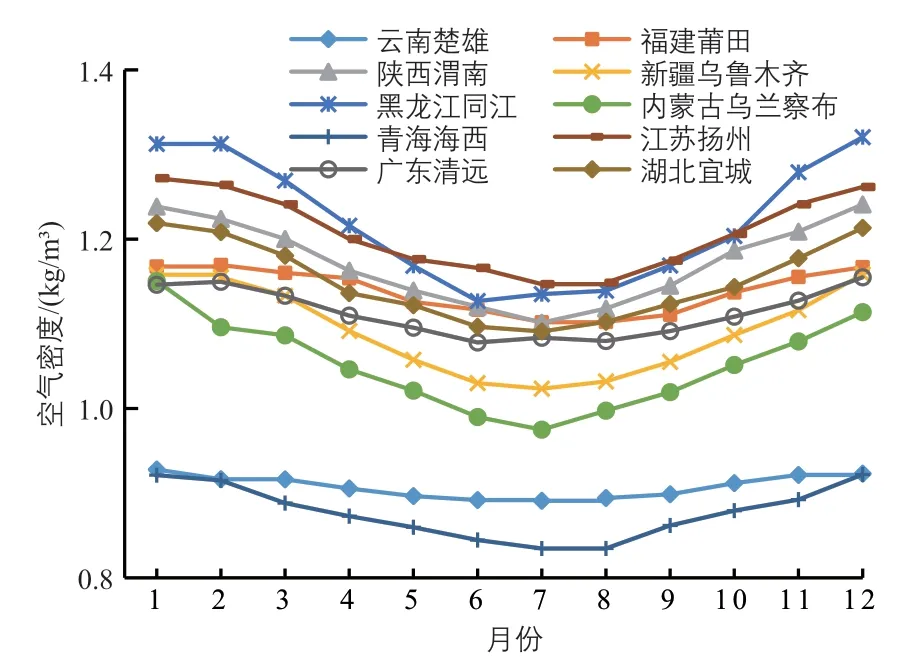
图1 各代表区域的空气密度的年变化幅度Fig. 1 Annual variation range of air density in each representative region
从表1~表3 和图1 可以看出:在中国,空气温度年变化幅度较大的地区(例如内蒙古乌兰察布和黑龙江同江),其空气密度的年变化幅度也较大,空气密度的月平均值标准差也较大,在0.050 kg/m3以上;空气温度的年变化幅度较小的地区,空气密度的年变化幅度也很小,空气密度的月平均值标准差也很小。
1.3 空气密度变化幅度的主要影响因素
为分析空气密度的主要影响因素,对空气密度标准差、空气温度标准差、大气压力标准差的相关关系进行分析。
对空气密度标准差和空气温度标准差做线性相关,相关关系图如图2 所示。相关方程式为y=0.0046x-0.0001,决定系数r2=0.8858,相关系数r=0.941,相关性非常好。
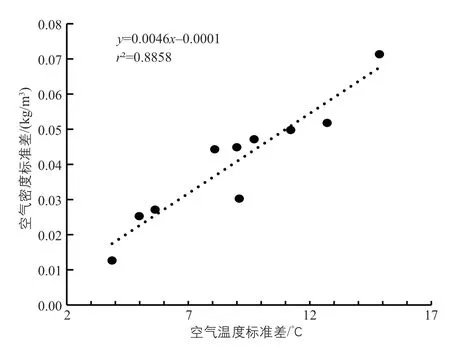
图2 空气密度标准差与空气温度标准差的相关关系Fig. 2 Related relationship between air density standard deviation and air temperature standard deviation
对空气密度标准差和大气压力标准差做线性相关,相关关系图如图3 所示。相关方程式为y=0.0128x+0.0364,r2=0.0144,r=0.120,基本不相关。
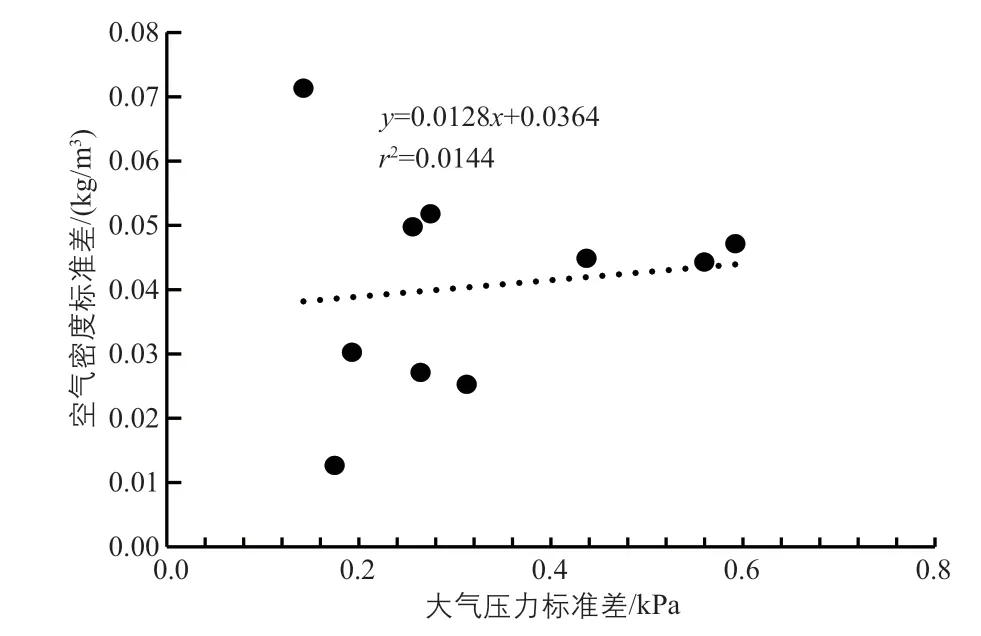
图3 空气密度标准差与大气压力标准差的相关关系Fig. 3 Related relationship between air density standard deviation and atmospheric pressure standard deviation
从表1~表3 可以进一步统计得到10 个代表区域测风塔测得的空气密度年平均值为1.093 kg/m3,年平均值标准差为0.04 kg/m3,年平均值标准差占年平均值的3.66%;10 个代表区域测风塔的空气温度年平均值为11.2 ℃,年平均值标准差为8.92 ℃,年平均值标准差占年平均值的79.64%;10 个代表区域测风塔的大气压力年平均值为89.5 kPa,年平均值标准差为0.32 kPa,年平均值标准差占年平均值的0.36%。通过对年平均值标准差占年平均值的比率进行比较分析,发现大气压力的年平均值标准差占年平均值的比率很小,空气温度的年平均值标准差占年平均值的比率较大,即大气压力的年变化幅度很小,空气温度的年变化幅度较大。
从图2 和图3 可以分析得出:空气密度年变化幅度受大气压力年变化幅度的影响很小,受空气温度年变化幅度的影响较大。因此,四季空气温度差异大的区域,空气密度的年变化幅度也大;四季空气温度差异小的区域,空气密度的年变化幅度也小。
2 按某测风塔得到的不同值计算发电量的结果比较
选取上文10 个区域中陕西渭南的测风塔(记为1#测风塔),分别按空气密度年平均值(见表1)、空气密度月平均值(见表1)及空气密度时间序列值计算发电量,然后对发电量计算结果进行比较。由于该测风塔所在区域的空气密度年变化幅度较大,分析空气密度年变化情况对风电场发电量计算的影响有一定的典型性。年等效利用小时数为年发电量与装机容量的比值,因此为方便比较,本文以等效利用小时数代替发电量进行分析。
1#测风塔的塔高为100 m,不同高度处安装有风速传感器、风向传感器、空气温度传感器、大气压力传感器,传感器和记录仪均为美国NRG 品牌的测风设备。
1#测风塔的传感器和记录仪的配置情况如表4 所示。
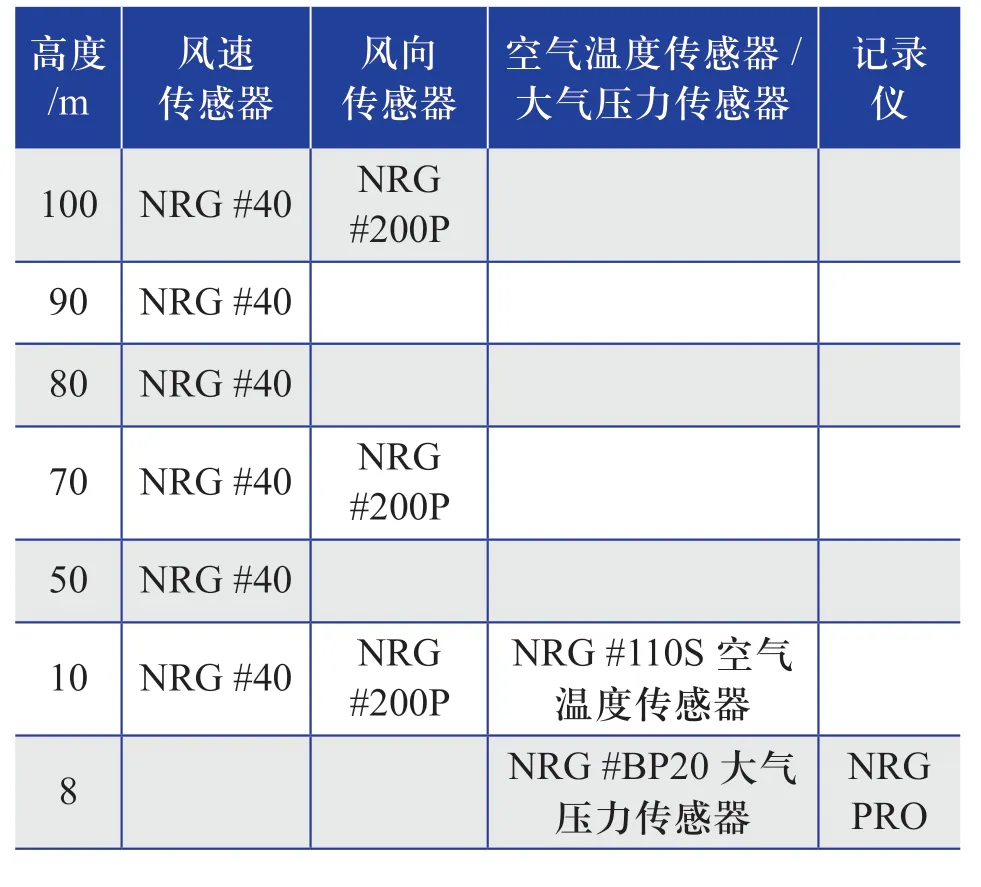
表4 1#测风塔的传感器和记录仪的配置情况Table 4 Configuration of sensors and recorders for 1 # wind measuring tower
2.1 按1#测风塔年平均空气密度计算的等效利用小时数
根据1#测风塔数据得到的年平均空气温度为15.6 ℃,年平均大气压力为97.5 kPa,使用式(1),可计算得到该区域的年平均空气密度为1.174 kg/m3。
选择浙江运达风电股份有限公司生产的WD156-3000 型号风电机组(下文简称为“运达WD156-3000 风电机组”),轮毂高度为100 m。在年平均空气密度为1.174 kg/m3、中等湍流强度的功率曲线下,测算测风塔单点的年等效利用小时数,空气密度折减系数取78%,则按年平均空气密度计算得到的年等效利用小时数为2301.22 h。
2.2 按1#测风塔月平均空气密度计算的等效利用小时数
统计1#测风塔每月的空气密度,依旧使用运达WD156-3000 风电机组(轮毂高度取100 m),空气密度折减系数取78%,按月平均空气密度计算1#测风塔单点的月等效利用小时数。
按1#测风塔月平均空气密度和年平均空气密度分别计算得到的等效利用小时数结果如表5所示,月等效利用小时数对比如图4 所示。
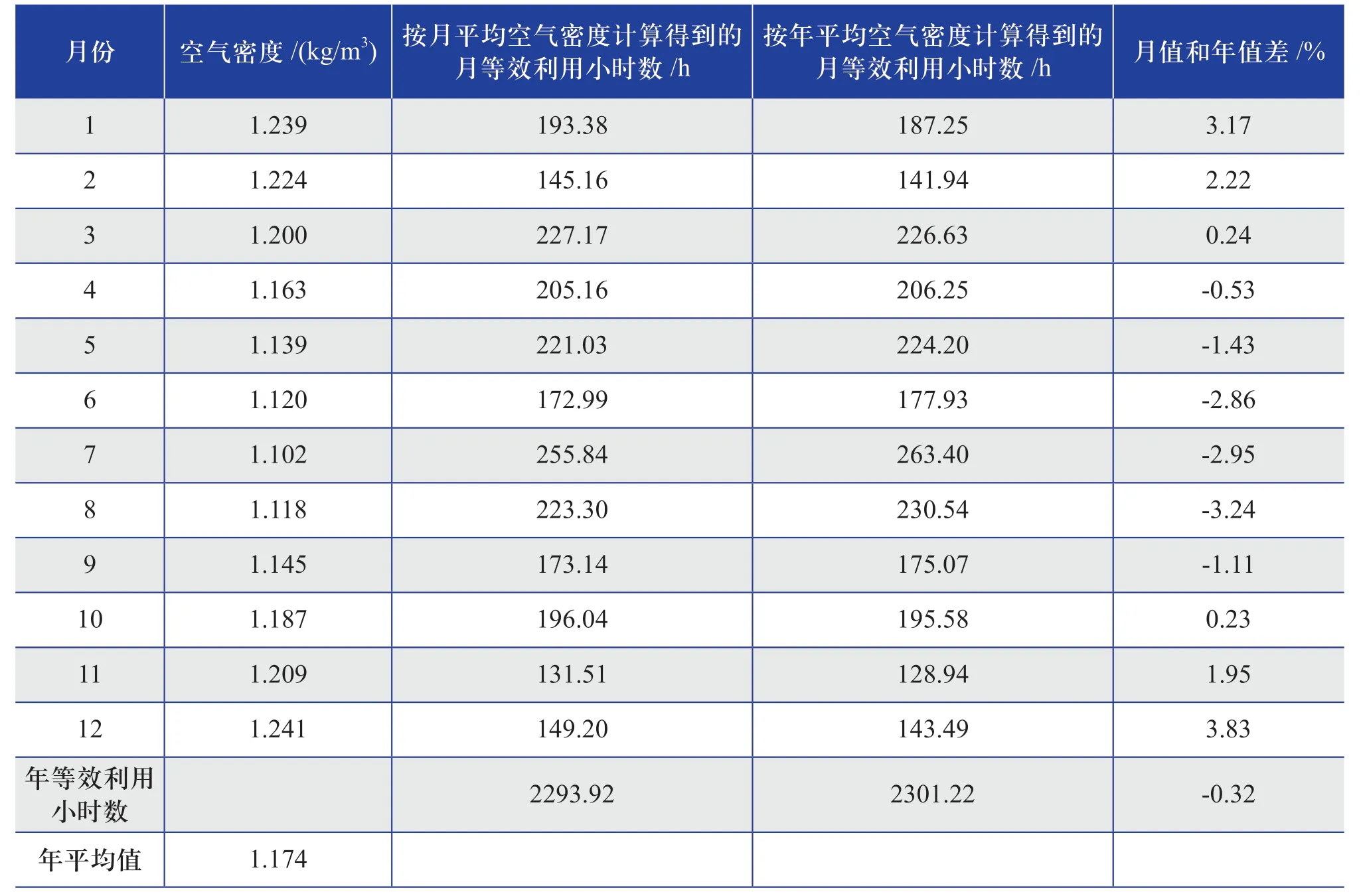
表5 按1#测风塔月平均空气密度和年平均空气密度计算的结果Table 5 Calculated results based on monthly average air density and annual average air density of 1 # anemometer tower
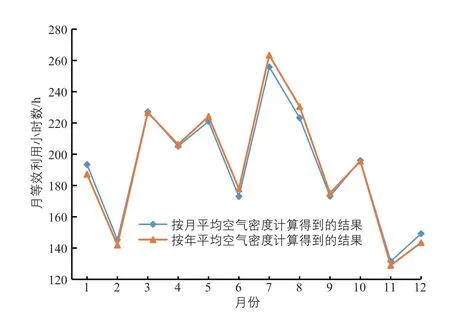
图4 按年平均空气密度和月平均空气密度分别计算得到的月等效利用小时数对比Fig. 4 Comparison of monthly equivalent utilization hours calculated based on annual average air density and monthly average air density
从表5 和图4 可以看出:使用月平均空气密度计算得到的年等效利用小时数为2293.92 h,使用年平均空气密度计算得到的年等效利用小时数为2301.22 h,差7.3 h,使用月平均空气密度得到的计算结果比使用年平均空气密度得到的计算结果低0.32%,总体差异不大。使用年平均空气密度和使用月平均空气密度计算得到的月等效利用小时数之间的差异最大为3.83%。使用年平均空气密度来计算月等效利用小时数时,由于夏季时的空气密度低于年平均空气密度,得到的结果属于高估;冬季时的空气密度高于年平均空气密度,得到的结果属于低估。
2.3 按1#测风塔空气密度时间序列值计算的等效利用小时数
1#测风塔记录仪每10 min 记录1 组数据,包含风速、风向、空气温度、大气压力等数据。使用1#测风塔每10 min 的空气温度和大气压力,计算每10 min 的空气密度,精确到0.01 kg/m3,可得到1#测风塔全年的空气密度时间序列值,其中,全年空气密度时间序列值的最小值为1.06 kg/m3,最大值为1.31 kg/m3。
依然使用运达WD156-3000 风电机组(轮毂高度取100 m),按照0.01 kg/m3空气密度间隔的功率曲线、空气密度折减系数取78%,计算1#测风塔单点的等效利用小时数序列,并统计年等效利用小时数。计算得到的年等效利用小时数为2297.41 h,与使用月平均空气密度计算得到的年等效利用小时数(2293.92 h)相比高3.49 h,即高了0.152%;与使用年平均空气密度计算得到的年等效利用小时数(2301.22 h)相比低3.81 h,即低了0.166%,差异均较小。
2.4 小结
在实际应用中,如果要考虑风电场发电的月度出力情况,为了精确起见,使用对应的月平均空气密度计算风电场发电量更精确;若只是为了计算风电场年发电量,使用月平均空气密度和使用年平均空气密度计算发电量得到的结果差异不大。
3 结论
本文在中国范围内各种地形和气候条件下,选择了10 个具有代表性的区域,对代表性区域测风塔数据中的空气温度、大气压力、空气密度进行分析,并选取其中空气密度年变化幅度较大的陕西省渭南市的1 座测风塔分析空气密度年变化情况对风电场发电量计算结果的影响。分析结果如下:
1)空气温度年变化幅度较大的地区,空气密度的年变化幅度也较大,空气密度的月平均值标准差也较大,在0.050 kg/m3以上;而空气温度年变化幅度较小的地区,空气密度的年变化幅度也很小,空气密度的月平均值标准差也很小。
2)比较分析年平均值标准差占年平均值的比率,大气压力的年平均值标准差占年平均值的比率很小,空气温度的年平均值标准差占年平均值的比率较大,即大气压力的年变化幅度很小,空气温度的年变化幅度较大。
3)空气密度年变化幅度受大气压力年变化幅度的影响很小,受空气温度年变化幅度的影响较大。四季空气温度差异大的区域,空气密度的年变化幅度也大;四季空气温度变化小的区域,空气密度的年变化幅度也小。
4)计算风电场发电量时,使用月平均空气密度计算得到的年等效利用小时数比使用年平均空气密度计算得到的低0.32%;使用空气密度时间序列计算得到的年等效利用小时数比使用月平均空气密度计算得到的高0.152%,比使用年平均空气密度计算得到的低0.166%,差异均较小。
使用年平均空气密度和使用月平均空气密度计算得到的月等效利用小时数之间的差异最大为3.83%。使用年平均空气密度来计算等效利用小时数时,由于夏季时的空气密度低于年平均空气密度,得到的结果属于高估;冬季时的空气密度高于年平均空气密度,得到的结果属于低估。在实际应用中,如果要考虑风电场发电的月度出力情况,为了精确起见,使用对应的月平均空气密度计算风电场发电量更精确;若只是为了计算风电场年发电量,使用月平均空气密度和使用年平均空气密度计算发电量得到的结果差异不大。
