小策略在数学教学中的“启思”运用

顾立军

在小学数学教学中，存在教学内容比较抽象而教材中没有呈现具体解算方法的情况，从而导致学生单凭基础知识很难想到解题方法和思路。此时，如果教师能巧妙运用一些特定的策略来引导学生深入思考，将有助于他们灵活自如地解答此类问题。下面，本文就来谈谈教师在教学中如何巧妙运用一些小策略启发学生思考，从而促进学生更好地习得知识、掌握方法、学会思考。

1.标箭头，让思考过程明了直观

学生解题时思考之所以会“卡壳”，很多情况下是因为他们找不到恰当的思考“起点”，抑或是不知下一步该怎样往下写（算），只能估摸着想到一步算一步。此时，如果教师能引导学生通过画箭头来辅助学习或思考，将能起到化繁为简、化难为易的作用，同时能将一些抽象深邃的数学知识转化为学生直观明了的思考过程。例如，苏教版六上经常出现如图1 所示的练习题，学生如果不能掌握解答要领，即找不到填写的关键数，不清楚该如何一步步往下算和填，就很可能会全部填错。如果教师引导学生找准填算起点（已知数），再由已知数出发画箭头依次计算填写其他数，学生很容易便能逐步填出其他数。

（图1）

2.画导图，让思考层次拾级而上

很多情况下，例题教学并不能涵盖所有练习题的情况，而且由于教材篇幅的限制，大多数例题都偏重于方法教学，对于其中的算理、内涵、意义的讲解多侧重于最主要的部分，对于完整思考解算过程的讲解也或多或少会留一些空白。如此，学生解答后面的练习题时，方法自然有点生疏，思考也更多地停留在模仿层面，解答一些类似的题目还能应付，题型稍有变化时便犯难了。如果此时教师能引导学生画一画例题主要解算方法的思维导图，让学生依据导图来理解例题中方法的来龙去脉，不仅有助于学生掌握其中的算理，而且能使学生的思考从被动接受转为主动理解，思考层次拾级而上。例如，苏教版四年级有许多列竖式计算的题目，学生如果不理解其中的算理，做再多题目也不能知其所以然。如果教师教学时能引导学生画导图来理解算理的计算步骤和得数的意义（格式举例如图2 所示），将有助于他们看清每一步计算的意义和书写的对应位置，从而明晰怎样去计算。

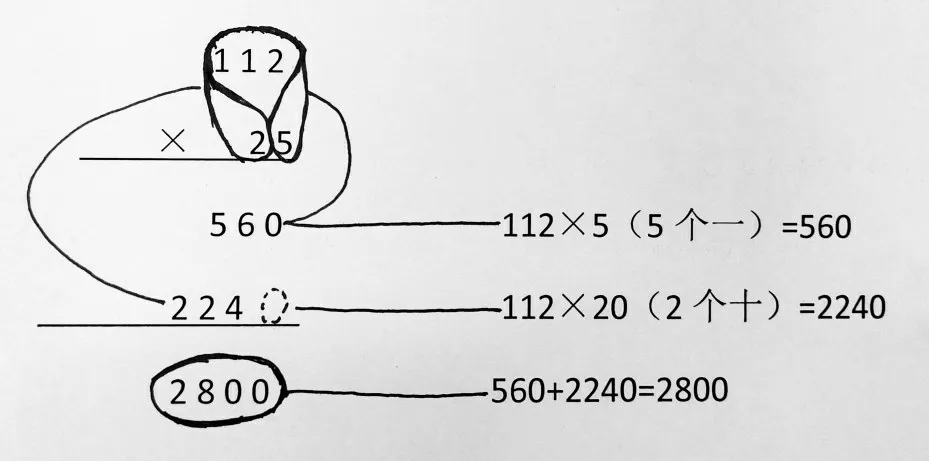
（图2）

3.举实例，让思考空白清晰完整

有些题目的解答方法千变万化，且需要多步复杂的过程，但教材中对一些题目的解答过程并没有详细说明。小学生的思维以直观形象为主，很难做到抽象地全程思考，特别是面对一些有字母或符号参与其中的选择、判断、比较、计算、说理等类型的题目，有时候只能猜个答案应付。这时就需要教师帮学生搭建思考的“脚手架”，如可以引导学生举实例来代替题目中的一些字母、符号进行判断或计算，让学生摸不着头脑的思考空白变得清晰直观可入手。例如，苏教版四下经常出现这样的练习题：根据a×b＝45，在下面的横线上填上合适的数。（a÷5）×（b×5）＝____；（a×10）×（b×10）＝____。这里就可以根据a×b＝45，举实例a＝5、b＝9，那么，（a÷5）×（b×5）＝1×45＝45，（a×10）×（b×10）＝50×90＝4500，从而让原本需要的复杂思考过程变得清晰完整。

4.巧迁移，让思考支撑有据可依

尽管已经掌握了基础知识和方法，有些学生在后续练习时遇到不断变化的题目，依据例题中的数量关系依然很难准确解答，特别是面对一些应用分数、小数来解决的问题时，因前后数量颠倒依然可以计算，学生更是难以确定思路，也难以科学正确地检查出对错。此时，如果教师引导学生通过迁移来看到这类题目的解答思路类似于以前学过的相关题型，将能使他们清楚地知道该如何来思考和解答，数学学习的成就感和自信心也会倍增。例如，苏教版六年级经常会出现分数除法的实际问题，比如吨稻谷可碾米吨，平均每吨稻谷可碾米多少吨？每碾1 吨米需要多少吨稻谷？很多学生虽然知道用除法计算，但不怎么清楚用哪个数除以哪个数及其意义解释，因而有时候两个问题的列式会“张冠李戴”。如果教师教学时能引导学生迁移到以前比较熟悉的整数情况，用整数5来代表，用整数3来代表，“学生就会比较容易理解：把3 吨米平均分成5 份，其中的1 份就是1 吨稻谷碾出的米，所以第一个问题整数情况的列式是3÷5，迁移到分数除法列式就是把5 吨稻谷平均分成3 份，一份就是碾1吨米需要的稻谷，列式是5÷3，迁移到分数除法列式就是。由此，学生的思考和思路依靠整数情况的支撑便变得有理有据。

总之，一个小策略的运用虽然只能解决个别类型的问题，但只要教师在教学中不断开动脑筋、总结经验，巧妙运用小策略启发学生思考，努力激发学生不断发现和创新使用小策略，必将有助于学生不断迸发出新的思考活力。