借助数字教材资源 优化数学课堂教学
2023-07-21覃蓓
覃蓓


[摘 要]人教版数字教材配备文本素材、图片素材、视频、动画、互动习题和学科工具(计算器、GeoGebra软件)等资源,教师可根据教学需要,适当运用数字教材资源,优化课堂教学。文章以“勾股定理”教学为例,阐述如何在课堂导入、探索新知、课堂练习、课后作业等教学环节中运用数字教材资源优化课堂教学。
[关键词]数字教材资源;优化;数学课堂教学;勾股定理;核心素养
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2023)08-0007-03
人教版数字教材以《义务教育数学课程标准(2011年版)》为基础,以人教版义务教育教科书为蓝本,借助数字技术配备了丰富的教学资源,比如文本素材、图片素材、视频、动画、互动习题和学科工具(计算器、GeoGebra软件)等。教师应合理利用现代信息技术给学生提供丰富的学习资源,设计生动的教学活动,以促进数学教学方式方法的变革。
下面以人教版数字教材八年级下册中的“勾股定理”(第一课时)的教学为例,阐述如何借助数字教材资源优化课堂教学。
一、教学案例设计
(一)教学内容和目标分析
“勾股定理”(第一课时)的教学内容是勾股定理的探究、证明及简单应用。
《义务教育数学课程标准(2022年版)》对“勾股定理”提出的学习要求是探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题。 这节课的教学目标:(1)经历勾股定理的探究过程;(2)能运用勾股定理解决一些简单的问题。
(二)教学过程
1.课堂导入
教师播放数字教材第21页的短视频,介绍国际数学家大会。(如图1)
教师在图1处暂停,让学生观察2002年在北京召开的国际数学家大会的会徽,提出问题1。
问题1:同学们见过这个图案吗?在这个图案中,你看到了哪些几何图形?
在学生独立思考、回答的基础上,教师引出本节课的内容:关于直角三角形,我们已经知道它的两个锐角互余。在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。 那么,直角三角形还有哪些性质呢?我们一起来研究吧!
2.探索新知
教师使用聚光灯功能将数字教材第22页中的图17.1-1放大,让学生观察并提出问题2。
问题2:相传2500多年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的图案反映了直角三角形三边的某种数量关系。同学们,今天我们就一起来研究这个图案。通过观察这个图案,你们有什么发现?
学生思考并回答。
教师出示图2。
问题3:大家想一想,图2乙中阴影部分的三个正方形的面积有什么关系?
经过思考,有学生把图2甲看成是由许多个等腰直角三角形组成的,通过数等腰三角形的个数,发现两个较小的正方形的面积之和等于较大的正方形的面積。有学生认为通过移动、拼接,两个较小的正方形中的等腰直角三角形可以拼成较大的正方形,由此得出相同的结论。
教师引导学生思考:请大家继续思考,图2乙中的三个正方形所围成的[△ABC]的三边之间有什么关系?
根据正方形的面积等于边长的平方,学生很容易发现:[AB2+AC2=BC2],即[△ABC]的两条直角边的平方和等于斜边的平方。接着,教师播放数字教材第22页“思考”栏目中的短视频,引导学生观察拼接的过程和结论的出现。
教师运用聚光灯功能将数字教材第23页的“探究”栏目放大。
问题4:等腰直角三角形有上述性质,那么其他直角三角形也有这个性质吗?
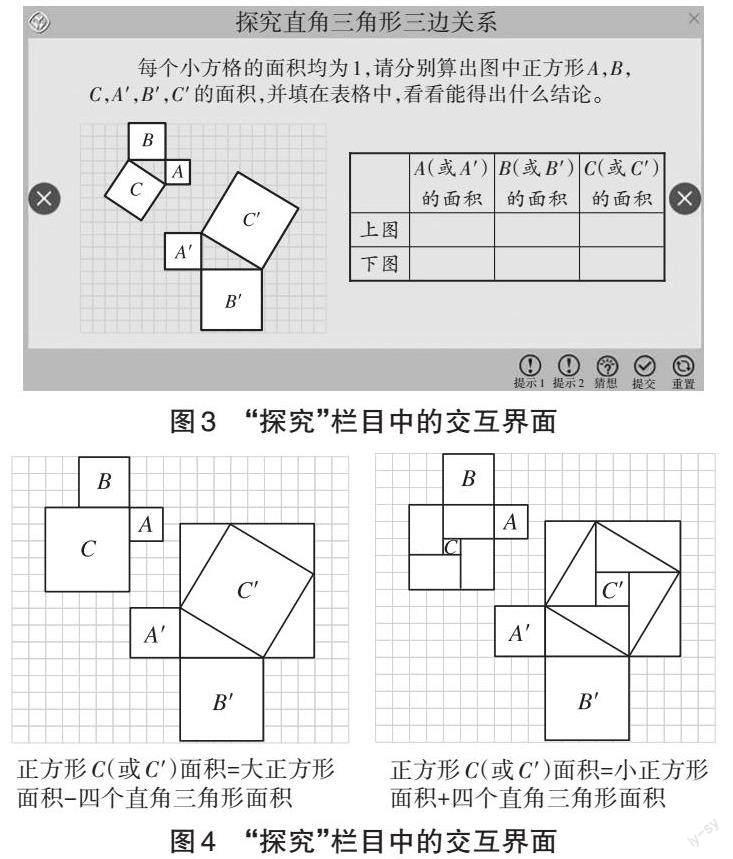
学生分小组讨论。教师巡视,然后打开“探究”栏目中的交互界面(如图3),让小组代表上台输入计算结果,同时说说本小组成员是如何计算的。比较难的是正方形C和C'的面积求解过程。有小组用“补”的方法,有小组用“割”的方法。学生在讲解时可以用电脑系统自带的笔或者希沃软件的笔(教师课前打开希沃软件)在交互界面上画线、书写。教师肯定了学生的回答后,先后点击“提示1”和“提示2”动态演示“补”和“割”的方法(如图4)。
类比等腰直角三角形三边关系的探索过程,学生得出:[DF2+EF2=DE2], [D'F'2+E'F'2=D'E'2],即直角三角形斜边的平方等于两直角边的平方和。
问题6:其他直角三角形也有以上性质吗?由此,你能猜想一般的直角三角形的三边之间有什么关系?
经过思考,学生认为对于一般的直角三角形,上面的结论也成立。教师引导学生把上述猜想表述为命题1:如果直角三角形的两条直角边长分别为[a]、[b],斜边长为[c],那么有[a2+b2=c2]。
问题7:命题1只是猜想,为了使它有说服力,我们需要对它进行证明,那么如何证明?
学生分小组活动,教师巡视。如果学生感到困难,教师则给出提示。提示一,脱离网格,并让直角三角形的边长一般化,尝试证明。提示二,阅读数字教材第23、24页,看看古人赵爽是如何证明的。根据提示一,教师打开刚才的交互界面,点击“猜想”后再分别点击左、右两边的图形,从而先后演示“补”的方法(如图6)和“割”的方法(如图7)。
为了渗透中华优秀传统文化,展现我国古人研究勾股定理的成就,教材介绍了赵爽的证法。赵爽的证法是一种面积证法,依据是图形经过适当切割后再拼接成一个新图形,切割、拼接前后图形各部分的面积之和不变,即利用面积不变关系和对图形的不同算法得到等量关系。
由于学生对面积法比较陌生,因此笔者首先安排学生阅读数字教材的第23、24页,了解赵爽证法,然后点击数字教材第24页图17.1-6右边的图标,打开交互界面,让学生观察图形的切割过程(如图8),再让学生尝试拖动、旋转交互界面中的五个图形拼成一个正方形,最后点击“演示”,动态演示两种拼接方法(如图9)。
教师出示数字教材第23页的图17.1-5,向学生说明“赵爽弦图”的由来,然后和学生谈谈勾股定理的相关史料,鼓励学生尝试自己证明。
3.课堂练习
练习1:数字教材第24页练习第1题。
练习2:数字教材第24页练习第2题。
设计意图:考查勾股定理的简单应用,即已知直角三角形的两边,求第三边。
4.课堂小结
回顾本节课,并请学生回答以下问题:
(1)今天我们学习了哪些主要内容?
(2)在探究勾股定理的过程中,我们经历了哪些过程?
5.课后作业
(1)阅读数字教材第30页的“阅读与思考“栏目,结合该页配备的动画,了解勾股定理的其他证明方法。
(2)通过上网等方式查找勾股定理的有关史料、趣事及其他证法。
(3)尝试自己找到一个新的证明方法。
二、借助数字教材资源优化课堂教学的思考
(一)根据教学设计选择适当的资源
数字教材为教师提供了丰富的教学资源,教师应根据教学设计选择适当的资源。比如,关于本节课,数字教材第22页左上方就配备了一个讲授本课内容的微课,但如果一开始就播放这个微课,那么学生不需要过多地思考、探究就可以知道勾股定理,后面的探究活动便难以再调动学生的学习积极性了,所以在教学中根本不需要播放该微课。
(二)根据资源特点选择适当的运用方式
教師可以根据资源特点选择适当的运用方式。比如,对于数字教材中的微课,笔者建议教师在播放前对微课即将讲解的知识做适当铺垫并让学生带着问题去听,在讲到重要知识时,教师可按暂停键做适当的强调或提醒学生记笔记。
(三)根据教学需要充分运用学科工具——GeoGebra软件
如果教师能充分运用学科工具——GeoGebra软件制作一些动画,效果也是非常不错的。比如,对于人教版数字教材七年级上册习题4.1中的第7题,教师可在课前运用GeoGebra软件制作正方体11种展开图的动画。这样在讲解本题时,便可以让学生在判断的基础上,折一折、画一画,然后动态演示正方体11种展开图,从而有效突破难点,并为将来引导学生顺利解决与正方体展开图有关的最短路径问题做好铺垫。
综上可知,数学教师应与时俱进,充分利用信息技术,合理使用数字教材资源优化课堂教学,发展学生的数学核心素养。
[ 参 考 文 献 ]
[1] 中华人民共和国教育部.义务教育数学课程标准:2022年版[M].北京:北京师范大学出版社,2022.
[2] 人民教育出版社,课程教材研究所,中学数学课程教材研究开发中心.义务教育教科书教师教学用书:数学八年级下册[M].北京:人民教育出版社,2013.
(责任编辑 黄桂坚)
