优选科学探究案例 优化课堂教学过程

程如林

［摘 要］在现行高中物理教材中，“简谐运动”的内容没有编入简谐运动的周期公式，这给教学造成了三个方面的缺憾。回顾历年的教材发现，在1979年版《全日制十年制学校高中课本·物理》中曾编入了周期公式，并通过“单位圆”进行了推导，在1984年版《高级中学课本·物理（甲种本）》中也给出了周期公式，但没有推导过程，在1984年版《高级中学课本·物理（乙种本）》中没有编入周期公式，在之后的各个版本教材中均不再出现周期公式。教材中曾经编入周期公式，说明它对教学是有帮助的，后来删除了周期公式，是因为受当时教学条件的限制，教学难度大，但在当前形势下，教学条件日益完善，在教学中是可以探究周期公式的。文章阐述了探究周期公式的重要性与可行性。

［关键词］探究案例；简谐运动；周期公式

［中图分类号］    G633.7        ［文献标识码］    A        ［文章编号］    1674-6058（2023）08-0051-05

在《普通高中物理课程标准（2017年版）》中，“科学探究”是高中物理学科四大核心素养之一，开展科学探究活动，可促进学生体验科学探究过程，领悟科学探究方法，增强科学探究能力，并加深对相关知识的理解。教师在教学过程中善于开展科学探究活动，可优化教学过程，提高教学效率。在现行各种版本的高中物理教材中，均编排了很多探究性教学案例。

开展探究式教学，仅利用教材中的探究案例是不够的，教师还要根据教学需要适时插入教材中没有的、由教师自主优选的探究案例。插入的探究案例是否恰当，主要看它对教学是否有帮助，如果它能优化课堂教学，提高课堂教学效率，就可以插入。本文介紹一个自主优选探究案例——探究简谐运动的周期公式。

一、探究缘由

在新人教版高中物理教材中，“简谐运动”这一单元的教学内容被编排在选择性必修第一册第二章第一节至第三节［1］中，在第一节内容“简谐运动”中，教材通过实验总结得出弹簧振子的位移—时间图像（即[x-t]图像）是正弦曲线，进而指出“这样的振动是一种简谐运动”；在第二节内容“简谐运动的描述”中，教材介绍了振幅、周期、频率、相位等物理量，并通过“做一做”栏目总结得出简谐运动的周期与其振幅无关的结论；在第三节内容“简谐运动的回复力和能量”中，教材阐述了“简谐运动的回复力”和“简谐运动的能量”两个重要概念，并通过“做一做”栏目讨论了能量的转化与守恒情况。

不难发现，教材没有给出简谐运动的周期公式。这样的编排，对教学是有缺憾的，这种缺憾主要表现在以下三个方面：一是没有这个公式，“简谐运动”这一单元的知识体系就显得不够完整，欠缺系统性，不利于学生全面、深刻地理解本单元的知识内容；二是没有这个公式，对后面单摆的周期公式来说，前后衔接不够紧密，过渡不够自然；三是没有这个公式，学生就搞不清简谐运动的周期到底与质量有什么关系，因为在单摆周期公式中周期与质量是无关的，而在弹簧振子振动过程中，通过观察发现，周期与质量是有关的，这两种振动都是简谐运动，但它们的周期与质量的关系是不一样的，学生对此感到疑惑，不理解，从而影响了教学效果。

如果在“简谐运动”这一单元的教学中穿插一个探究内容——探究简谐运动的周期公式，通过探究活动得出简谐运动的周期公式是[T=2πmk]，则在后面第4节“单摆”的教学中就可顺理成章地推导出单摆的周期公式，因为单摆是简谐运动，所以简谐运动的周期公式也适用于单摆，只要将单摆中回复力与位移关系的比例系数[k=mgl]代入，便可得出单摆的周期公式为[T=2πlg]。这样组织教学，不仅使整个简谐运动的知识体系显得完整并具有系统性，而且前后教学内容也实现了自然过渡，学生也明白了其中的内在逻辑关系，就不再疑惑了。

至此，我们知道，在“简谐运动”教学中插入这个探究内容对教学是有帮助的，那么，现行高中物理教材为什么没有编入简谐运动的周期公式呢？

二、教材回顾

回顾历年各种版本的高中物理教材发现，在1979年版《全日制十年制学校高中课本·物理》中，简谐运动的周期公式是有要求的，教材通过“参考圆”的辅助方法推导出了周期公式[T=2πmk]。从1984年秋季学期开始，我国高中物理教学开始使用新教材，当时的新教材有两种版本，即《高级中学课本·物理（甲种本）》和《高级中学课本·物理（乙种本）》，这两种版本的教材，其教学要求是不一样的，难度也是不一样的，甲种本要求较高，难度较大，乙种本要求较低，难度较小。在甲种本教材中，给出了周期公式[T=2πmk]，但没有给出推导过程，而在乙种本教材中，没有给出这个周期公式。在之后的各种版本教材中，就不再出现这个周期公式了。

从这个变化过程看，可以发现，关于简谐运动周期公式的教学，原先是有要求的，后来要求不断降低了。为什么会这样呢？因为在当时的形势下，学校教学条件有限，实验器材较少，实验设备落后，计算机等信息化教学手段还没有应用到教学中，也没有Excel等数据处理软件辅助教学，所以难以通过实验探究得出周期公式；另外，由于当时高中数学教材中没有编入导数知识，所以也难以通过导数知识开展理论探究，得出周期公式。鉴于当时的条件限制，在早期教材（1979年版）中，公式的理论推导只能采用“参考圆”的方法进行，但这种方法比较抽象难懂，教学效果不理想，之后，为了降低学习难度，在后来的甲种本教材（1984年版）中，就只给出了周期公式而没有给出推导过程，而在乙种本教材（1984年版）中就直接删除了这个周期公式，之后的各种版本教材中也就不再给出周期公式了。

但在当前形势下，计算机等信息化教学手段已普遍应用到教学中，Excel等数据处理软件也已普及，另外，在高中数学中也已编入了导数知识［2］，在高中物理教学中，教师是可以根据教学需要穿插这一教学内容的，即通过探究活动得出这个周期公式，下面介绍本人的教学实践过程。

三、探究过程

对周期公式的探究，既可以采用实验探究，也可以采用理论探究的方法。在理论探究中，还可以采用多种不同方法，既可以通过数学中的导数知识推导出这个公式，还可以通过物理学中的单位制理论推导出这个公式。

（一）实验探究

【探究内容】探究简谐运动的周期公式（分组实验）。

【探究器材】将班级学生分成5个实验小组，每个小组配备的实验器材如下：J2110螺旋弹簧组1组（内装5个弹簧，分别对应不同的劲度系数），铁架台1个，钩码多个（每个质量为50 g），秒表1个。

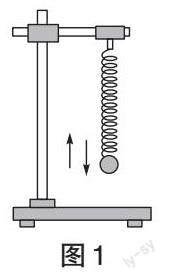
【探究过程】教师引导学生组装器材，制成竖直方向的弹簧振子（如图1），并观察弹簧振子的振动过程，猜想周期可能与振动的振幅、弹簧振子的质量、弹簧的劲度系数有关，进而采用控制变量法开展实验探究，可分为三个步骤进行。

1.控制弹簧振子的质量、弹簧的劲度系数不变，仅让振幅A发生变化，探究周期T与振幅A的关系。

（1）实验任务：各个实验小组分工协作，共同完成探究任务。要求每个实验小组选取相同的弹簧，相同质量的钩码（钩码的个数相同），制成弹簧振子，进行实验，分别测量振动周期，将数据记录在表格中，最后对数据进行综合分析。

（2）学生实验：在实验中，各个实验小组均选取了劲度系数为[k=10 N/m]的弹簧和2个钩码（总质量[m=100 g]），制成弹簧振子后开始实验，振幅随机确定，各个实验小组分别测出了发生N次全振动的时间，并求出了周期[T=tN]，将数据记录在同一张表格中，如表1所示。

（3）实验结论：观察表1中的数据，可知周期近似为一定值。从而得出结论：在误差允许的范围内，简谐运动的周期T与振幅A无关。

2.控制劲度系数k不变，让弹簧振子的质量m发生变化，探究周期T与质量m的关系。

（1）实验任务：各个实验小组分工协作，共同完成探究任务。要求每个实验小组选取相同的弹簧，不同质量的钩码（通过改变钩码的个数实现），制成弹簧振子，进行实验，分别测量振动周期，将实验数据记录在表格中，最后对数据进行综合分析。

（2）学生实验：在实验中，每个小组均选取了劲度系数为[k=15 N/m]的弹簧，另外，第1小组选取了1个钩码、第2小组选取了2个钩码……各个小组分别测出了各自的弹簧振子发生N次全振动的时间，并求出对应的周期[T=tN]，将数据记录在同一张表格中，如表2所示。

（4）实验结论：观察图像可知，[T2-m]图像是一条通过坐标原点的直线， 从而得出结论：当劲度系数[k]不变时，周期[T]与质量[m]的关系为[T2∝m]，即[T∝m]。

3.控制振子质量[m]不变，让劲度系数[k]发生变化，探究周期[T]与劲度系数[k]的关系。

（1）实验任务：各个实验小组分工协作，共同完成探究任务。要求每个实验小组分别选取各不相同的弹簧，相同质量的钩码（钩码的个数相同），制成弹簧振子，进行实验，分别测量振动周期，将实验数据记录在表格中，最后对数据进行综合分析。

（2）学生操作：在实验中，每个小组均选取了两个钩码（总质量[m=100 g]），另外，第1小组选取了劲度系数为2.5 N/m的弹簧、第2小组选取了劲度系数为5 N/m的弹簧……各个小组分别测出了各自的弹簧振子发生N次全振动的时间，并求出了周期[T=tN]，将数据记录在同一张表格中，如表3所示。

（4）实验结论：观察图像可知，[T2-1k]图像是通过坐标原点的直线，从而得出如下结论。

当振子质量不变时，周期[T]与劲度系数[k]的关系为[T2∝1k]，即[T∝1k]。

4.师生总结：综合以上三个步骤中的结论，可得 [T∝mk]，令比例系数为[k0]，则[T=k0mk]，可由图像求得为[k0≈6.28]，即[k0≈2π]，从而得周期公式[T=2πmk]。

【探究结论】弹簧振子做简谐运动的周期公式为[T=2πmk]。

点评：以上探究过程是典型的实验探究过程，其中包含了科学探究的各个要素，包括：提出问题、进行猜想、设计方案、进行实验、记录数据、数据处理、得出结论、交流展示。整个探究过程科学严谨，对学生起到了示范引领作用，学生体验了探究过程，领悟了探究方法，提升了探究能力。另外，在实验过程中用到了控制变量法，以及用计算机软件处理数据的实验方法，这些思想方法都是物理学中最基本和最重要的思想方法，学生领悟了这些思想方法，也就增强了实验素养。

（二）理论探究

1.用数学中的导数知识进行探究

当前，导数知识已被编写进了高中数学教材中，导数知识在物理中的应用很多，不仅可用于定性判断、定量计算和求解极值，还可用于探究物理规律。本案例就可以用导数知识进行探究，过程如下：

（1）关于简谐运动的位移—时间关系，教材中给出了这样的关系式[x=A sin（ωt+φ）]。

（2）根据导数知识，得简谐运动的瞬时速度为[v=dxdt=Aωcos（ωt+φ）]。

（3）根据导数知识，得简谐运动的瞬时加速度为[a=dvdt=-Aω2sin（ωt+φ）]。

（4）比较步骤（1）（3）中的两个关系式，可得[a=-ω2x]。

（5）对简谐运动来说，回复力[F回=-kx]，由牛顿第二定律得[a=F回m=-kxm]。

（6）比较步骤（4）（5）中的关系式，得[-ω2x=-kxm]，即[ω2=km]。

（7）因为[ω=2πT]，代入上式，可得[T=2πmk]。

點评：用导数知识开展探究教学，看似好高骛远，其实不然，它的意义在于不仅获得了有用的结论，更为重要的是，它展示了数学知识和物理知识的融合运用过程，这是新课程提倡的教学方法，可以促进学生核心素养的提升。

2.用物理学中的单位制理论进行探究

在现行高中物理教材中编排了单位制的内容，教师和学生通常熟悉它的两种用途：（1）在进行计算时，若已知量均采用国际单位制中的单位，则计算过程中不用代入单位，只要在计算结果末尾写出所求量的国际单位即可；（2）可用单位制来判断物理表达式是否正确，如果表达式两边各物理量单位经换算后不相同，则表达式一定错误。其实，单位制理论还有一个重要用途，就是用来探究物理规律、开展探究教学。

利用单位制理论探究简谐运动周期公式的过程如下：

（1）师生观察。观察简谐运动的过程后发现，周期可能与下列三个因素有关：振动的振幅A，振子的质量m，弹簧的劲度系数k。

（2）师生猜想。T与A、m、k之间的关系式可假设为[T=k0Axmykz] （其中[k0]为比例系数，无单位，x、y、z的数值待定）。

（3）师生推导。用“物理公式两边单位相同” 这一理论去推导上式中x、y、z值。

在表达式[T=k0Axmykz]中，周期T的单位是s，振幅A的单位是m，质量[m]的单位是kg，劲度系数k的单位是[N·m-1]，这个单位可转化成基本单位的组合，即[N·m-1=kg·m·s-2·m-1=kg·s-2]，将各个物理量的单位代入表达式[T=k0Axmyk]z两边进行运算，

点评：用单位制理论开展探究教学，不仅使学生巩固了课本中的单位制知识，而且使单位制的应用功能得到拓展，这样的教学过程，学生很感兴趣，也很受启发。

四、教学反思

回顾整个教学过程，不难发现此项探究活动具有以下特性。

（一）探究内容具有适切性

本案例探究的周期公式在过去的教材中曾经出现过，后又删除了，出现过这个公式说明它对教学有帮助，后来删除了这个公式，是受当时的教学条件限制而做出的调整。在当今形势下，学校已经拥有了优良的实验设备，教师已经用上了先进的数据处理软件，学生已经储备了足够的数学知识，所以进行探究的条件已经成熟了，现在再次将该案例引入课堂教学，是可行的，也是切合时宜的。

（二）探究方法具有多样性

《普通高中物理课程标准（2017年版）》明确提出：“科学探究活动的方式应多样化。”［4］在本案例中，科学探究可以用实验方法，也可以用理论方法，理论方法也有多种。教师在教学中要善于挖掘这些新方法，这样可以启发学生思维，激发学生的学习兴趣。

（三）探究结论具有实效性

本案例的探究结论——简谐运动的周期公式，具有实效性，它既对“简谐运动”这一单元教学内容进行了充实，使其知识结构呈现完整性和系统性，又对后面的“单摆”教学做了铺垫。有了简谐运动的周期公式，便可顺利推导出单摆的周期公式，消除了学生的疑惑，可谓一举多得。

［   参   考   文   献   ］

［1］  人民教育出版社，课程教材研究所，物理课程教材研究开发中心.普通高中教科书物理选择性必修第一册［M］.北京：人民教育出版社，2020：32-45.

［2］  苏教版高中数学教材编写组.普通高中教科书数学选择性必修第一册［M］.南京：江苏凤凰教育出版社，2021：173-196.

［3］  中華人民共和国教育部.普通高中物理课程标准：2017年版［S］.北京：人民教育出版社，2018：70.

（责任编辑 易志毅）