学习进阶理论视域下的小学生计算思维测评框架

【摘 要】有效的测评是科学、有序地推进小学阶段计算思维教育的必备条件。基于学习进阶理论，依据结构中心设计法，构建小学生计算思维测评框架。测评框架包含进阶变量、成就水平和学习表现，其中进阶变量分为计算概念、计算实践和计算观念，成就水平从低到高依次为识别、理解、设计和问题解决。测评框架开发与使用促进了学生核心素养的发展。

【关键词】计算思维；学习进阶；测评框架；小学生

【中图分类号】G434  【文献标志码】A  【文章编号】1005-6009（2023）26-0068-05

【作者简介】邓志贤，甘肃省武山县城关镇上街子小学（甘肃武山，741300）教师，一级教师。

信息技术的快速发展重塑了人们沟通交流的时空观念，改变了人们的思维方式。当前，计算思维作为信息化社会中数字公民所应具备的基本素养，备受重视。［1］115我国《普通高中信息技术课程标准（2017版）》已明确将计算思维列为信息技术学科的核心素养之一。小学是我国义务教育的起始阶段，从小学阶段开始实施计算思维教育，对提升学生数字公民素养、推动社会信息化发展具有重要价值，而科学、有序地推进计算思维教育发展的重要依据在于对学生学习过程和结果开展有效的测评。传统测评框架在构建方法和组成要素上强调了依据学科知识逻辑确立维度和指标，对学生真实的思维发展过程重视不够。基于学习进阶理论构建的测评框架不仅能对学生所学知识和技能的掌握程度进行有效的“测”，还能对其计算思维能力水平进行精准的“评”，对我国小学生计算思维测评具有重要的借鉴意义。

一、相关概念与理论基础

1.计算思维

计算思维并不是一个新的概念，早在1980年，西蒙·派珀特首次使用了计算思维一词，其指代算法思维和程序思维，强调思维的逻辑性，并提出应用计算机可提高思维能力、改变知识建构的模式。尽管早期计算思维的相关研究已萌芽，但是直到2006年，周以真教授发表了题为《计算思维》的文章，计算思维才正式作为一个研究对象受到人们的重视。周以真教授认为，计算思维是利用计算机科学的基础概念解决问题、设计系统和理解人类行为的思维过程和方法，其本质是抽象的。虽然该定义较为经典，但其权威性并未得到业界的一致认可，尤其是计算思维的本质、内涵及外延等都不是很明确。因此，众多研究者又从不同角度提出了计算思维的定义，但都并未形成共识，存在“活动及方法说”“系统说”“过程说”和“问题解决说”等界定。［1］116-117布伦南等人基于对Scratch编程实践的研究提出了计算思维三维框架——计算概念、计算实践和计算观念。由于该框架具备较强的可操作性和通用性，被广泛地应用于计算思维的研究和测评中。

2.学习进阶

学习进阶这一术语是美国国家研究理事会在2005年K-12年级科学成就测验政府工作报告中提出的。报告将学习进阶界定为“对学生在一定时间跨度内学习和探究某一主题时依次进阶、逐级深化的思维方式的描述”。构建学习进阶的本质是针对科学大概念，通过实证测量以确定学习者的认知发展路径。学习进阶一般包含5个组成要素：学习目标、进阶变量、成就水平、学习表现和评估工具。学习目标是学生达到一个阶段进阶终点时的表现；进阶变量是指核心概念以及基于核心概念的关键实践；成就水平是思维发展过程中的多个中间层级；学习表现是处于不同发展层级的学生完成相应任务时的表现；评估工具是指一套基于假设模型的测量学生发展的工具。学习进阶的开发一般采用结构中心设计法。［2］结构中心设计法的“结构”是指学生的心理构造，通过它来建构学生的认知要素及发展模型，即结构必须阐述需从哪些方面刻画学生学习的心理状态，这些方面随着时间的发展分为哪几个关键的进阶层级。结构中心设计法包含5个步骤：明确目标、展开描述、提出进阶、收集数据和分析结论。结构中心设计法能详细说明如何对结构进行拆解，如何确定预期的学习进阶，并在这个过程中注重利用已有研究成果以及提供教学策略。

3.SOLO分类理论

SOLO分类理论是约翰·B.彼格斯等人在皮亚杰认知发展阶段理论的基础上提出的一种高阶思维能力形成过程的层级框架。彼格斯认为，一个人回答某个问题时所表现出的思维结构是可以检测的，并称之为“可观察的学习成果结构”。据此，彼格斯将学生回答问题时的思维结构分为5个层次，分别为前结构、单点结构、多点结构、关联结构以及抽象扩展结构。［3］前结构是指学生对问题的理解处于感知阶段，依靠感觉经验回答问题；单点结构是指学生能根据单个问题线索给出解决问题的思路；多点结构是指学生能根据多个问题线索给出解决问题的思路，但是线索之间是孤立的，没有联系的；关联结构是指学生不仅能根据多个问题线索给出解决问题的思路，还能对多个问题线索进行归纳总结；抽象扩展结构是指学生能将问题线索进行概括，并综合应用系统化、抽象化的理论分析解决问题。从前结构到单点结构，再到多点结构，是思维结构量变的过程；从多点结构到关联结构，再到抽象扩展结构，是思维结构质变的过程。SOLO分类理论对学生思维发展和学习表现之间的关系进行了深入的阐释，由此成为学习进阶开发的重要理论基础。

二、小学生计算思维测评框架构建

学习进阶理论为当前我国小学生计算思维测评框架构建提供了方法和内容上的参考。研究依据结构中心设计法，遵循“理论预设—验证分析—修改完善”的基本思路，通过“进阶要素的确定—进阶变量的提取—成就水平的划分—学习表现的描述—专家和教师验证”5个步骤构建小学生计算思维测评框架。

1.進阶要素的确定

学习进阶的5个要素中，学习目标也是进阶终点，与最高阶的成就水平具有内在的一致性，在本研究中并不作为单独的进阶要素；成就水平需要基于学习进阶开发具体的学习进阶测评工具，是对学习进阶的验证和操作化实施，将会在示例部分进行阐释，在本研究中也不作为单独的进阶要素。依据研究问题和研究目的，最终确定3个进阶要素用于构建测评框架：进阶变量、成就水平和学习表现。

2.进阶变量的提取

进阶变量的提取过程是确定测评框架的维度和指标的过程，其经历了以下4个步骤：一是依据布伦南等人提出的计算思维三维框架确定3个进阶变量——计算概念、计算实践和计算观念，即测评维度；二是结合美国计算机科学教师协会等机构发布的计算思维概念框架和我国2017年颁布的高中信息技术课程标准，以及部分已有实证研究的成果，确定组成各进阶变量的核心要素，即测评指标；三是对各个核心要素内涵进行理论分析，删除或合并内涵重叠的要素，完善进阶变量；四是对进阶变量及其核心要素进行归类整理，并描述解释，确立进阶变量。核心要素是对各个进阶变量的进一步细化和描述，旨在为各个进阶变量在不同成就水平上的学习表现描述提供依据。

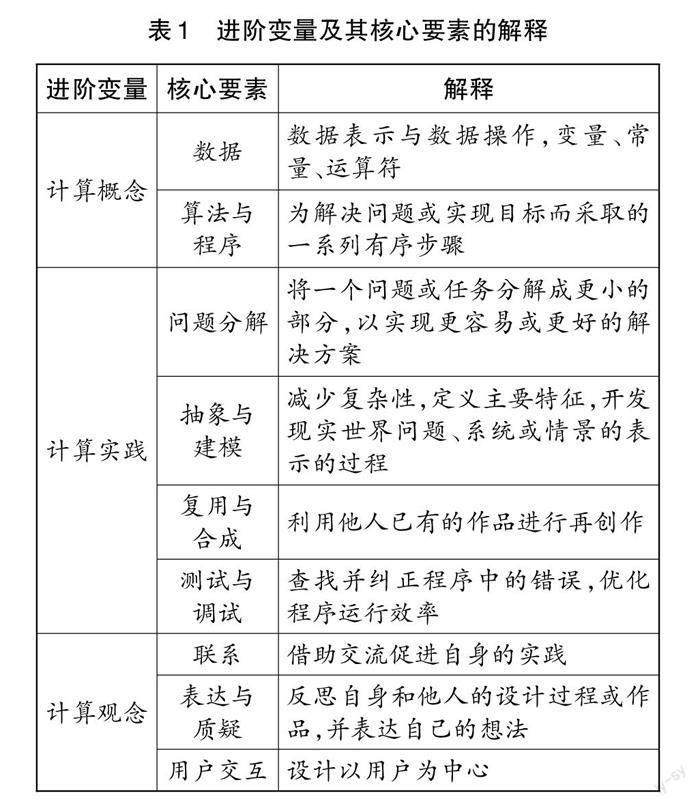
在进阶变量与核心要素提取的过程中，本研究依据以下4个标准对相关概念进行了删选：一是概念本身过于泛化，不够明确，不具备计算思维的显著特征，如逻辑思维、系统思维等；二是概念并不是计算思维过程的一部分，只是应用计算思维进行问题解决的结果或特征，如模块化等；三是概念所代表的实践可被其他实践代替，不具备独立性，如递增与迭代、评估等；四是概念超出小学生认知发展水平，尽管能被学生简单了解，但不能作为计算思维测评的内容，如系统以及理解复杂系统。最终确立了进阶变量与核心要素（如表1所示）。

[进阶变量 核心要素 解释 计算概念 数据 数据表示与数据操作，变量、常量、运算符 算法与

程序 为解决问题或实现目标而采取的一系列有序步骤 计算实践 问题分解 将一个问题或任务分解成更小的部分，以实现更容易或更好的解决方案 抽象与

建模 减少复杂性，定义主要特征，开发现实世界问题、系统或情景的表示的过程 复用与

合成 利用他人已有的作品进行再创作 测试与

调试 查找并纠正程序中的错误，优化程序运行效率 计算观念 联系 借助交流促进自身的实践 表达与

质疑 反思自身和他人的设计过程或作品，并表达自己的想法 用户交互 设计以用户为中心 ][表1 进阶变量及其核心要素的解释]

3.成就水平的划分

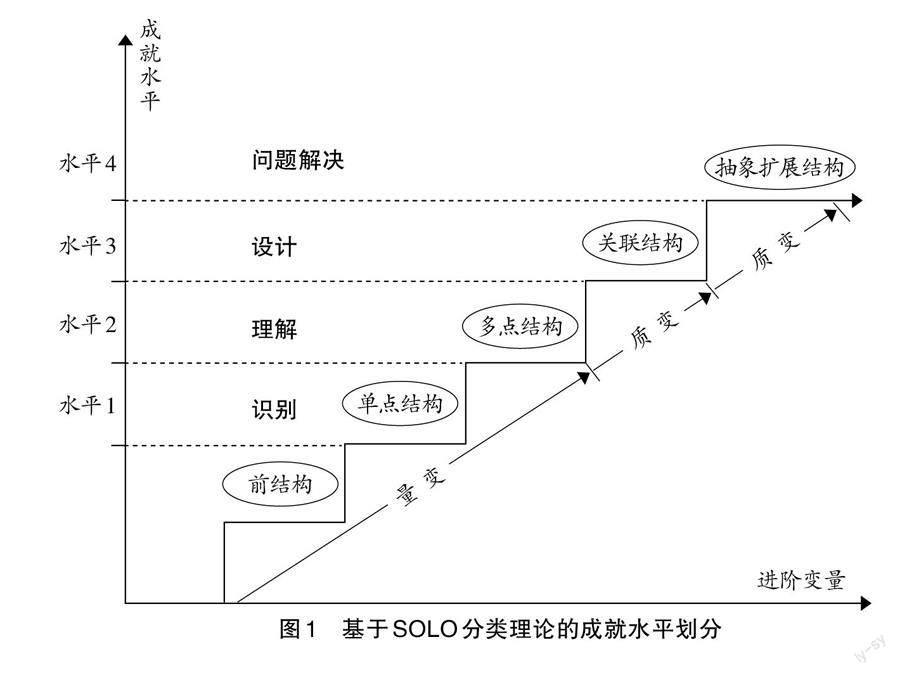
成就水平描述了学生在某一概念或实践上的思维发展阶段，也就是学习进阶中不同的“阶”。维尔纳等人将计算思维发展水平划分为理解、设计和问题解决3个层次，依据SOLO分类理论，其分别对应多点结构、关联结构和抽象扩展结构。维尔纳强调的是利用编程解决问题能力的阶段划分，因此对于前结构和单点结构层次并未做详细阐释。学生在达到理解水平之前，还需经历对编程的特征认识阶段，也就是SOLO分类理论中的单点结构。另外，前结构层次描述了学生面对问题情景时的初始状态，考虑到学生的个体差异和测评的可操作性，前结构水平并不作为单一成就水平层次进行划分。因此，最终确定小学生计算思维成就水平包括“识别”“理解”“设计”“问题解决”4个层次（如图1所示）。

水平1“识别”是指认识程序与编程，能操作程序单个指令。处于这一水平的学生能认识程序的基本结构和编程的过程，并对编程的指令模块进行单独操作，但还不能描述程序的执行过程，也不能理解一个完整的程序。水平2“理解”是指理解程序并能对单个程序指令进行简单改动。处于这一水平的学生能通过学习概念和简单编程案例，描述程序的执行流程并预测简单程序的结果，对单个指令能进行改动，但还不能独立设计程序。水平3“设计”是指能从模式集合中构建程序，并使用过程技巧解决问题。处于这一水平的学生能对多个案例程序进行模仿，并能改变其属性值或参数，得到不同的结果，但是不能编程解决新的问题。水平4“问题解决”是指学习可转移的问题解决技能，并在新的和不同的问题情境中使用。处于这一水平的学生能从学習的特定编程案例中总结出一般的编程模式和技巧，使之系统化，并能创造性地解决问题。

4.学习表现的描述

Scratch编程工具在小学阶段的计算思维相关课程中使用较为普遍，而已有关于计算思维测评的实证研究也多采用Scratch作为测评环境，评估学生的计算思维发展水平。因此，本研究采用Scratch工具作为计算思维能力外显的实践环境，描述学生的学习表现。研究从Scratch在线社区中挑选了不同阶段的小学生作品，以及从我国实施计算思维教育的小学校收集的大量Scratch作品案例，重点对不同阶段学生的编程设计模式、使用编码块类型、代码复杂程度等进行对比分析，最终确定学习表现的描述内容，初步构建了小学生计算思维测评框架。

5.专家和教师验证

本研究通过访谈收集专家和一线教师对测评框架的意见和建议，修改并完善框架。依据研究目的和研究问题，访谈选取的对象包括国内高校从事计算思维教育研究的专家4名，以及从事小学计算思维教育的一线教师5名。访谈内容围绕“进阶变量与核心要素的确定、成就水平的划分、学习表现的描述”3个方面展开。依据专家和教师访谈结果，研究对测评框架进行了如下修改：一是一线教师普遍表示，计算观念中的部分“用户交互”在小学各阶段中的表现并不明显，不适合作为小学生计算思维测评内容，因此删除了“用户交互”指标；二是以“问题解决过程的表示”为核心进一步明确了“抽象和建模”指标的学习表现描述；三是以“问题解决过程解释”为核心进一步明确了“算法与程序”指标的学习表现描述。另外，依据访谈结果，对测评框架中学习表现的描述也进行了修改和完善，最终确立了基于学习进阶的小学生计算思维测评框架（如表2所示）。

有效的测评是科学推进计算思维教育的重要基础。本研究依据学习进阶理论，基于计算思维三维框架，构建小学生计算思维测评框架，开发测评试题示例，分析了测评的方法和实施过程。与传统的测评框架相比，基于学习进阶构建的测评框架更重视学生在不同维度和指标上的学习表现和思维发展过程，测评的目的定位为以促进学生发展为核心的形成性评价，而非总结性评价。基于本研究，未来的研究重点将聚焦在从认知科学的视角探究计算思维的思维本质和能力结构，验证测评框架在理论上的科学性；基于心理测量学理论开发计算思维测评工具，实施大规模测评，验证测评框架在实践中的有效性。

【参考文献】

［1］张立国，王国华.计算思维：信息技术学科核心素养培养的核心议题［J］.电化教育研究，2018（5）：115-121.

［2］王磊，黄鸣春.科学教育的新兴研究领域：学习进阶研究［J］.课程·教材·教法，2014（1）：112-118.

［3］约翰·B.彼格斯，凯文·F.科利斯.学习质量评价：SOLO分类理论［M］.高凌飚，张洪岩，译.北京：人民教育出版社，2010.