具有Kagome结构磁振子晶体中平带及带隙的研究

张 璐, 杨 慧, 曹永军, 范天舒, 张 劼

(内蒙古师范大学 物理与电子信息学院,内蒙古 呼和浩特 010022)

平带晶格是指具有至少一个完全无色散布洛赫带的周期性介质,1980年就被人们所熟知[1-3],但当时许多人认为它们要么是“病态”的(需要复杂的晶格设计并且对扰动不稳定),要么是微不足道的(在理想的平带内,所有状态都是退化的,所以没有动态);然而最近,在物理学的各个领域,包括冷原子、电子凝聚态系统和光子学[4-7]等领域,对平带的研究兴趣重新燃起,因为人们开始意识到越来越多的具有短程连接的更简单的平带模型的例子[2,8-9];先进的制造技术使这些“病态”模型最终能够在实验室得以实现[10-11].此外,在具有平带结构的系统中引入诸如相互作用之类的扰动时,会出现一些有趣的现象[12-14].因此,平带受到了越来越多的关注,这种关注必然会随着理论和实验的进一步深入而继续下去.

量子霍尔效应是凝聚态物理中最有意义的发现之一[15],它将拓扑引入到物理学中,由此开始了拓扑能带的相关研究.拓扑现象在电子系统[16]、光子系统[17-18]都有研究,在人工晶体,如光子晶体、声子晶体中的研究也有所突破[19-26].2005年,Haldane和Raghu突破性地提出在光子晶体中实现光学拓扑态,由此光子学中引入了拓扑物理概念.随后对平带物理的研究持续并深入,使平带也得到广泛研究,在光子晶体、超构材料与光子晶格等光学系统中观察到了很多新的物理效应[19-21].最新研究进展是平带对应波函数群速度为0,可以实现整个布里渊区的慢光效应[22].Nakata等[23]构建了Kagome结构并直接观察到太赫兹波等离激元平带,在二维Lieb结构中也观察到类似性质[24].Huang等[25]在四方结构中实现了零折射率超构材料,且得到与Lieb结构相似的能带.2016年,Baboux等[26]在一维枕型结构中观察到无色散平带,得到了对应于平带的激子-极化激元凝聚态.2010年,日本研究团队[27]在具有烧绿石结构的铁磁体中首先发现了磁子霍尔效应.2013年,Hoogdalem等[28]理论证实了磁子霍尔效应的存在.在对具有拓扑性质的准粒子进行深入研究的过程中,美国研究小组[29]通过实验观察到Kagome磁铁中存在拓扑量子态.2015年,美国的研究小组[30]通过实验研究证实,在绝缘的Kagome铁磁体中,磁振子具有拓扑性质的能带结构,中子散射测量的结果也说明Kagome晶格中有一个平坦的能带.2017年,研究人员[31]根据磁子能带的Berry曲率导出磁子霍尔热导率.2020年,Xing等[32]通过最近邻海森堡相互作用与DM相互作用研究了具有Kagome晶格铁磁体中的天然磁子晶体的平带及拓扑性质.

磁振子晶体是类似于声子晶体和光子晶体的一种人工晶体,是由2种或多种不同磁性材料构成的具有空间周期性的人工微纳米复合材料[33-35],其最基本的特点是自旋波在其中传播时会受周期性结构调制而产生带隙,带隙范围内的自旋波不能在晶体中传播.Vasseur等[36]研究发现,构成晶体材料的相关参数不同会对带隙结构产生很大影响,会改变磁参数,交换作用常数相差越大对带隙的产生越有利.Cao等[37-39]研究发现,构成晶体的材料形状、大小和排列方式也会对能带隙结构产生影响.磁振子晶体相关应用多数依赖于其能带结构中产生的带隙.最近,林基哲等[40]又研究了蜂窝(honeycomb)结构磁振子晶体,发现在该结构中存在磁子狄拉克点与类狄拉克点.然而,关于磁振子晶体中平带及其拓扑性质的研究仍处于空白阶段.为此,本文中,笔者在上述研究的基础上,提出了具有Kagome结构的磁振子晶体模型,研究其相关平带性质.磁振子晶体、人工磁振子晶体中平带的出现完善了拓扑物理学的研究内容,在自旋波波导器件等领域有着广阔的应用前景,同时在量子计算、量子模拟等领域具有重要的研究价值.

首先提出了Kagome磁振子晶体结构模型,给出了计算方法,然后讨论了平带、狄拉克点和带隙,最后给出了相应的结论.

1 理论模型和计算方法

Kagome磁振子晶体的结构如图1a所示.圆柱材料A按Kagome结构严格排列在基底材料B中.其中,圆柱的半径为R,相邻距离为a.图1b所示为第一布里渊区.

图1 Kagome磁振子晶体结构示意图(a)和Kagome晶格的第一布里渊区(b)Fig.1 A Schematic Map of Magnonic Crystals with Kagome Structure(a) and the First Brillouin Zone of a Kagome Lattice(b)

忽略阻尼效应的前提条件下,自旋波在基底材料B中的传播行为可以用下面的方程描述:

(1)

其中,g代表磁旋比,g>0,Heff(r,t)是作用于M(r,t)上的有效场,而M(r,t)是材料磁化强度的矢量.利用改进的平面波展开法[39],可对Kagome磁振子晶体结构的带结构进行研究,交换作用系数α(G-G′)结果可以表示为

(2)

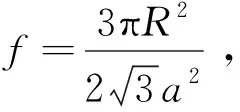
2 结果与讨论

对于二维Kagome磁振子晶体的带结构,具体数值计算过程是通过改变Kagome结构中排列在氧化铕(EuO)基底材料中的铁(Fe)圆柱的体积填充率来展开的.交换作用常数A和自发磁化强度Ms在计算过程中所选取的数值如下:

通过计算大量不同体积填充率下的带结构发现有平带出现.图2a为体积填充率f=0.65时Kagome磁振子晶体的带结构图.可知,第10条带接近平带,除在Γ点附近发生细微突变,其他部分均为平带;第14,15条带为完全平带且互相简并,第19,20条带也接近平带,除在Γ点附近发生细微突变,其他部分均为平带,也互相简并.说明在Kagome磁振子晶体中,通过调整体积填充率可以构建出平带.同时计算得到了第13～16条带相应的三维色散关系图.图2b为在K点附近局部放大的三维色散关系图.可见,第14,15条带是非常平的带,说明它们的平坦度非常高.

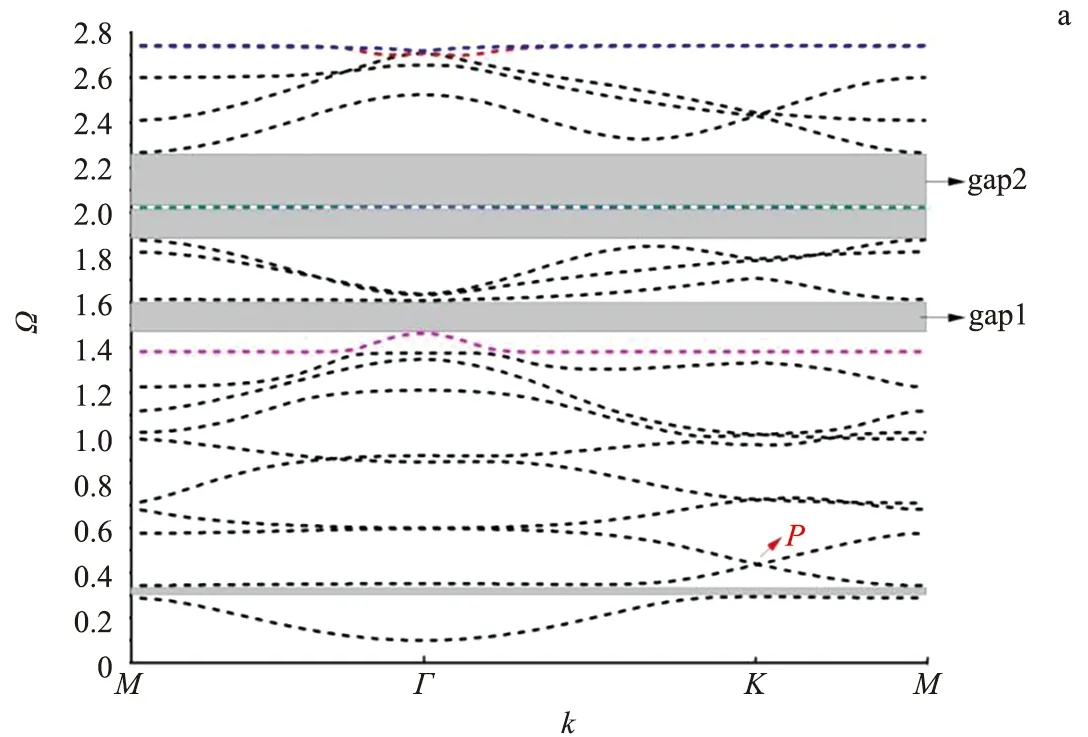
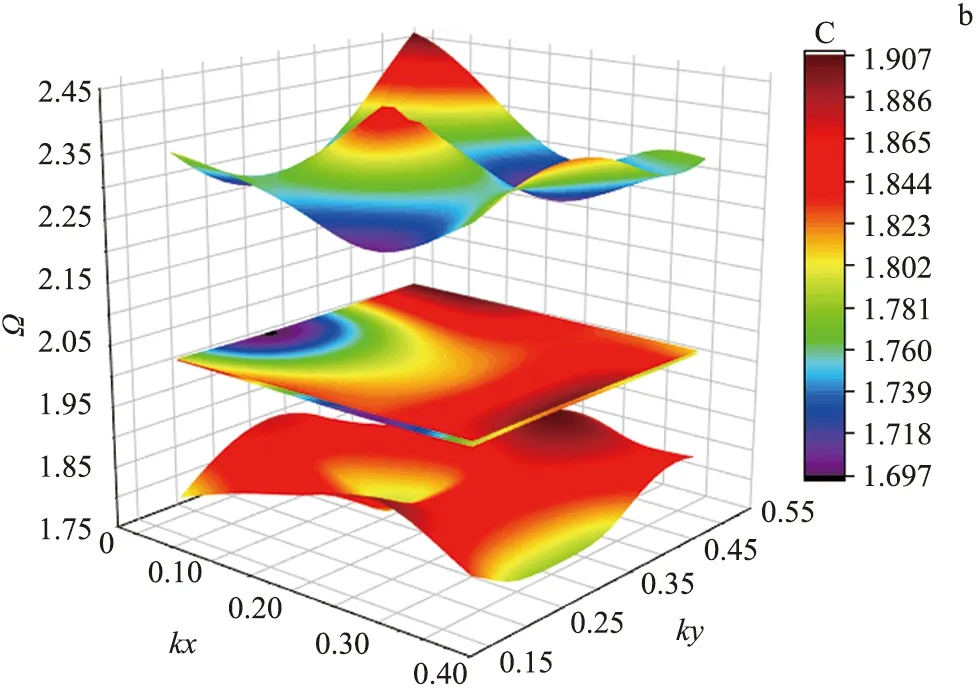
图2 Kagome磁振子晶体的带结构(a)及Kagome磁振子晶体中平带的三维色散关系图(b)Fig.2 Band Structure of a Kagome Magnonic Crystal(a) and Three-dimensional Dispersion Diagram of Flat Band in Kagome Magnonic Crystals(b)

平带处的行为在实空间的能量场分布也有所反映,如图3所示.图3a,b,c分别给出了f=0.65时第10,14,15条带在K点的能量场分布结果.其中,虚线圆表示圆柱散射体的位置,红色对应的值最大,即能量最高.从图3可以看出,能量很好的局域在基底氧化铕(EuO)中,散射体位置没有能量,说明平带的局域性非常强.对于第14,15条带,极化强度方向彼此相反.

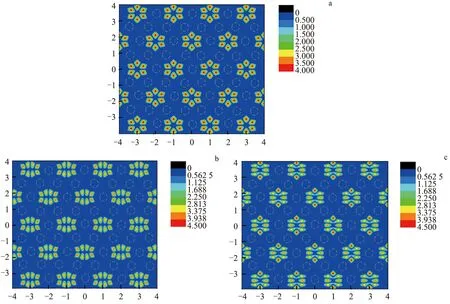
a.第10条带; b.第14条带; c.第15条带.图3 平带处的能量场分布Fig.3 Energy Field Distribution at Flat Band

平带随体积填充率f的变化关系结果如图4所示.图4a中离散的点表示平带只在某一个体积填充率时出现过,如f=0.20时,Ω=0.024 48,在第14条平带出现过,之后随着体积填充率的变化平带消失;同时当f=0.20时,在第10,15,19,20条平带开始出现.图4中相同的点线之间围成的区域表示连续存在平带的宽度,宽度较大说明平带的平坦度较低,宽度较小甚至重合说明平带的平坦度较高,如第10条平带从f=0.30处开始宽度较大,说明此时平带的平坦度较低,随填充率变化到f=0.50处开始重合,说明平带的平坦度非常高.从图4还可以发现,同一条平带在不同体积填充率下出现的位置也不同,如第10条平带在f=0.50时的频率约为1.082 59,在f=0.54时的频率约为1.156 88.图4b给出了第10条平带随体积填充率f的变化关系的放大结果.通过上述讨论发现,随着体积填充率的变化,平带的数目和位置都会发生变化.

图4 平带(a)及第10条平带(b)随体积填充率f的变化行为Fig.4 The Change of Flat Band with the Volume Filling Rate f (a)and the Change of the Tenth Flat Band with the Volume Filling Ratef(b)

从图2a还可以发现,在体积填充率f=0.65时,在布里渊区K点有2条能带相交,记作点P,且有严格的线性关系在其附近形成了狄拉克点.狄拉克点是K点二重态必然简并导致形成的,这种简并又是由于其结构具有对称性.狄拉克点在之前研究过的类石墨烯结构中也出现过[40].

从图2a还可以看到一些灰色区域,它们表示能带之间的带隙,图2a所示为体积填充率f=0.65时的带隙情况,在频率范围内共有4个完全带隙出现.

图5给出了带隙宽度随体积填充率的变化行为.选取其中2条带隙具体说明,分别是第10,11条带之间的带隙和第15,16条带之间的带隙,记为gap1和gap2.分析可得,带隙不是在任何体积填充率下都出现,同时其变化行为都是先增大后减小的.gap1,gap2均在f=0.55时达到最大,带隙宽度分别为ΔΩ=0.249 89,0.215 97.

3 结束语

利用平面波展开法研究二维Kagome磁振子晶体带结构发现,通过调节体积填充率,不仅可以构建平带,而且可以改变其数目和位置,同时在一定的体积填充率下会出现狄拉克点,此外,通过调节体积填充率也可以改变该结构中带隙的宽度和位置.期望通过研究人工磁振子晶体带结构实现对自旋波的调控和优化,提供相应理论基础和可行方案来设计并应用于磁振子晶体平带结构工程材料中.