腐蚀条件下的海底悬跨管道振动分析

骆正山，王香红

（西安建筑科技大学管理学院，陕西西安 710055）

0 引 言

海底油气管道是海上油气田开发生产系统的主要组成部分，随着服役时间的增长，腐蚀老化问题对其安全性的影响越来越明显。由于海床不规则或海流的冲刷作用易造成管道悬跨，在一定的海流条件下，管道会出现涡激振动现象［1］。腐蚀和涡激振动引起的疲劳损伤是导致海底油气管道失效的主要原因，海底油气管道一旦失效，会造成经济损失和环境污染等严重后果［2-4］。

近年来，国内外学者对管道腐蚀缺陷和涡激振动特性进行了广泛研究。MOTTA 等［5］和ARUMUGAM等［6］采用非线性有限元法对腐蚀管道进行了失效压力计算，提高了管道失效压力预测的准确性。MOHAMED等［7］基于M5 模型树和蒙特卡洛模型对腐蚀管道进行了可靠性分析，讨论了腐蚀缺陷的几何形状对失效概率的影响。于桂杰等［8］和黄坤等［9］通过有限元模拟对海底腐蚀管道的剩余强度进行了评价，结果表明，通过有限元仿真能准确计算出管道的剩余强度，腐蚀深度是影响管道强度的主要因素。傅忠尧［10］对不同腐蚀条件下海底管道的强度进行了评估，结果发现腐蚀深度和环向角度均会对管道应力产生显著影响，腐蚀长度对管道应力的影响不大。XIAO等［11］基于计算流体动力学（Computational Fluid Dynanics，CFD）方法，在自由跨管道涡激振动数值模拟的基础上考虑管土相互作用，提高了涡激振动预测结果的可靠性。JOSHI 等［12］提出了基于延迟分离涡模拟的湍流输运方程的有界保正变分方法，对细长柔性立管的涡激振动进行了数值研究。TEIXEIRA等［13］和MATS等［14］结合水动力系数载荷模型，提出了针对管道涡激振动响应的时域算法。安振武等［15］和肖荣鸽等［16］根据悬跨管道振动方程分析了管道在输送介质、外流速度和管道外形尺寸等因素影响下的振动特性，为海底管道的安全运行提供理论依据。高喜峰等［17］对非对称边界约束下海底悬跨管道的涡激振动疲劳特性进行了分析，结果发现管道两端土体扭转刚度对管道疲劳损伤值有一定的影响，填补了悬跨管道疲劳研究中有关非对称边界研究的空白。吴学敏等［18］提出了一种考虑大变形的深水立管涡激与参激耦合振动力学模型，并在该模型的基础上研究了参数激扰对涡激振动响应的影响。

综上，以往研究人员在研究管道腐蚀和涡激振动过程中提出了不同的方法和模型，但很少对腐蚀条件下海底悬跨管道的涡激振动进行研究。海底环境极为恶劣，海底管道普遍带腐蚀缺陷工作，因此对考虑腐蚀作用的悬跨管道开展涡激振动研究很有必要。鉴于此，本文在欧拉-伯努利梁理论和改进的尾流振子模型的基础上提出含腐蚀缺陷的海底悬跨管道涡激振动模型，并利用ABAQUS有限元软件对比验证该模型的有效性，进而深入分析腐蚀深度对海底悬跨管道涡激振动响应的影响，提高海底管道稳定性评估的可靠性。

1 模型构建

1.1 管道振动基本方程

由于海底管道长细比较大，可忽略其剪切变形，故将管道悬跨段视为柔性梁，采用Euler-Bernoulli梁模型模拟悬跨管道。悬跨管道在海流的作用下同时受到顺流向的曳力和横流向的升力的作用，其中升力对涡激振动的影响远大于曳力，因此仅考虑管道的横向振动。

海底悬跨管道模型见图1，其悬跨长度为L，外径为D，横截面面积为A，管道内流体压强为P，轴向力为T，抗弯刚度为IE。假设：悬跨管道两端为简支支座；管道内流体速度为v；海流速度恒定为U；不计管道所受浮力和重力。

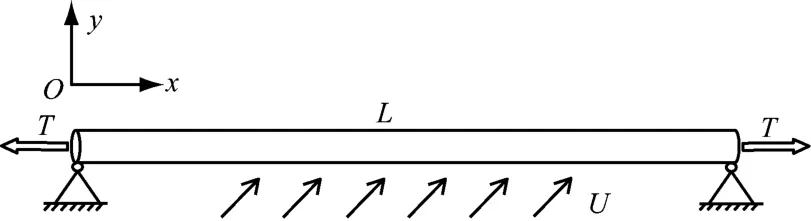
图1 海底悬跨管道模型

建立悬跨管道横向振动基本方程［19］，有

悬跨管道两端边界条件为

式（1）和式（2）中：y为管道横向位移，m；t为时间，s；m为单位长度管道总质量；m1为管道内单位长度流体质量，kg；c为阻尼；f（x，t）为悬跨管道在y方向上所受载荷。

1.2 含腐蚀缺陷管道涡激振动模型

当悬跨管道存在腐蚀缺陷时，其表面会产生微裂纹，直接影响管道的质量和刚度，并降低其可靠性。因此，基于裂纹梁的动力响应，考虑腐蚀条件下海底悬跨管道的振动方程［21］。管道壁厚为tb，抗弯刚度为IE0，在x ＝xi（i ＝1，2，…，N）处存在深度为h的腐蚀缺陷（0 ＜x1＜x2＜…＜xN＜L），将x ＝xi处的腐蚀缺陷i的等效扭转弹簧刚度记为Ki，则该腐蚀管道的等效抗弯刚度IEe可表示为

式（3）中：δ（x）为广义狄拉克函数。

海底悬跨管道在横向振动时受到的向上的涡激升力为

式（4）中：CL为上升力系数；ρw为海水密度，kg／m3。

由式（1）、式（3）和式（4）可得含腐蚀缺陷管道的涡激振动方程为

式（5）中：m0为管道单位长度质量，kg；m1＝ρfA为管内单位长度流体质量（ρf为管内流体密度，kg／m3），kg；

ma＝πcaρwD2／4 为管道附加质量（ca为附加质量系数，一般取1.0），kg；cs为管道外部阻尼系数；cf为管内流体阻尼系数。

1.3 尾流振子模型

在来流作用下海底悬跨管道两侧会交替形成强烈的漩涡，漩涡脱落会使悬跨管道产生周期性的振动，同时管道周围流体会受到升力作用下产生的涡激振动的影响。本文采用改进的范德波尔方程［20］的非线性振子模拟涡激振动的基本特征，表达式为

式（6）中：q ＝2CL／CL0为脉动升力系数，CL0为管道静止时的上升力系数，一般取CL0＝0.3；ε为经验参数，一般取ε ＝0.3；ωs＝2π·St·U／D为漩涡脱落圆频率（St为斯特劳哈尔系数，与雷诺数、波数和表面粗糙度有关，一般取0.2），Hz；Fq为管道对流体的作用力。Fq可表示为

式（7）中：K为管道对流体的耦合动力参数，一般取K ＝12。

1.4 数值求解

将悬跨管道均分成n份，每份作为1 个计算单元，得到n ＋1 个结点，依次标号为0，1，…，n。采用有限差分法对式（5）和式（6）进行离散求解，求得耦合振动方程的单元矩阵表达式为

式（8）和式（9）中：My和Mq分别为管道质量矩阵和流体质量矩阵；Cy和Cq分别为管道阻尼矩阵和流体阻尼矩阵；Ky和Kq分别为管道刚度矩阵和流体刚度矩阵。

运用Newmark-β方法对式（8）进行逐步积分，先给定初始时刻t0的脉动升力系数q0，以及悬跨管道的位移、速度和加速度，计算得到管道对流体的作用力Fq，再对式（9）迭代得到尾流振动参数q1，接着计算下一时刻管道的位移、速度和加速度，按此循环推导出不同腐蚀深度下的悬跨管道运动响应。

2 模型验证

2.1 有限元模拟

采用有限元软件ABAQUS分析腐蚀条件下海底管道悬跨段的动力响应，管道参数见表1。有限元单元采用C3D20R，为方便计算，选取轴向长度为0.5 m、环向1 周的腐蚀区域设置于悬跨管道跨中位置，对腐蚀区域网格进行加密处理。由于管道结构是对称的，故只取1／4 模型进行分析。腐蚀区域采用规则的弯曲长方形部分模拟；管道边界选取对称约束条件，设置为简支约束；管道所受载荷主要包括管道自重、管内流体自重、水流载荷和静水浮力。［10］选取海流速度U ＝0.3 m／s，腐蚀深度h ＝0.2tb，建立含腐蚀缺陷的管道有限元模型，见图2。

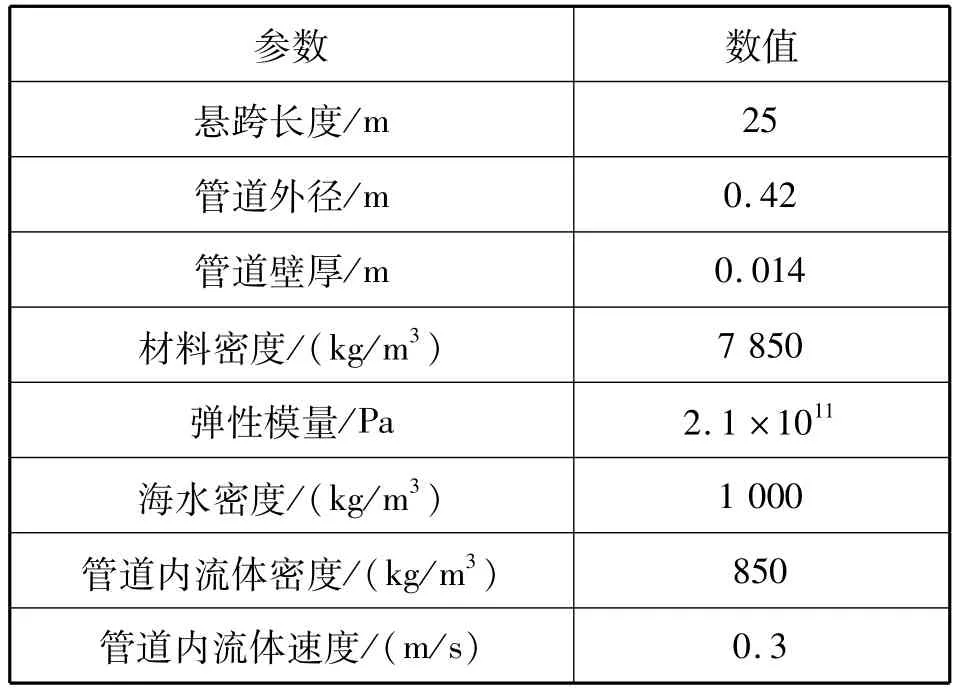
表1 管道参数

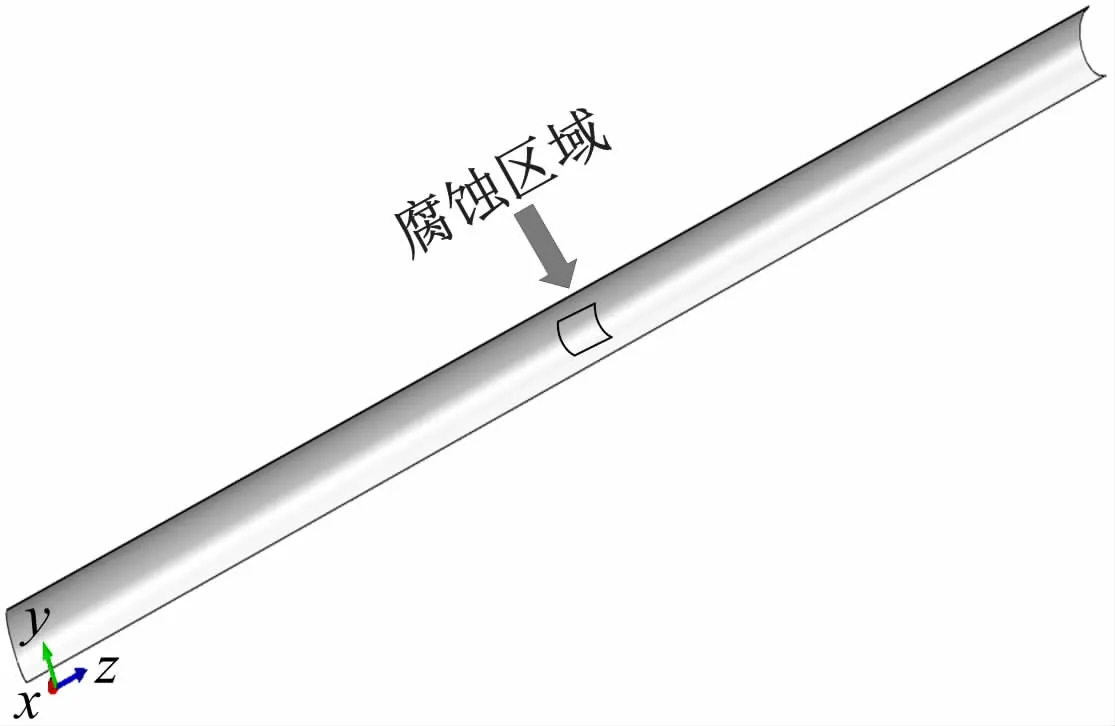
图2 含腐蚀缺陷的管道有限元模型

2.2 模拟结果与计算对比

以管道跨中位移时程为例，结合式（6）～式（9）开展理论计算，并将计算结果与通过有限元模型模拟得到的结果相对比，结果见图3。从图3 中可看出，考虑腐蚀缺陷的海底悬跨管道跨中位移时程曲线与通过ABAQUS模拟得到的结果基本吻合，验证了该涡激振动数值模型的正确性，可将其应用到含腐蚀缺陷的海底悬跨管道的涡激振动响应预测中。

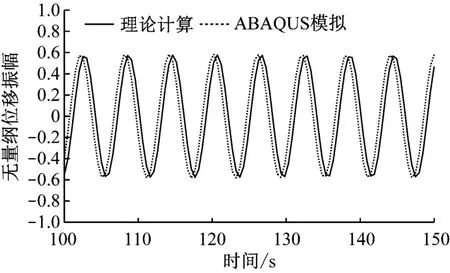
图3 海底悬跨管道跨中位移时程曲线

3 实例分析

根据本文建立的涡激振动数值模型，采用表1 所示管道参数，从管道的固有频率、位移响应和应力响应分析等3 个方面分析不同腐蚀深度下海底管道悬跨段的涡激振动情况。由于腐蚀具有随机性，将腐蚀简化为等深度的均匀腐蚀，腐蚀深度分别取0.1tb、0.2tb、0.3tb和0.4tb。

3.1 管道固有频率分析

悬跨管道的固有频率一般由管道的刚度、管道约束条件、管道悬跨段长度和管道质量等因素确定。根据梁结构的振动分析理论得到管道的固有频率fn的计算公式［15］为

式（10）中：C为常数，取决于悬跨管道端部约束情况，此处将管道两端简化为简支座，取C ＝1.57；M为悬空管道单位长度质量，kg／m。

图4 为U ＝0.3 m／s时不同腐蚀深度下悬跨管道固有频率的变化情况，腐蚀深度为零表示管道未被腐蚀。由图4 可知，随着腐蚀深度的增加，海底管道悬跨段固有频率减小，且其变化率逐渐增大。

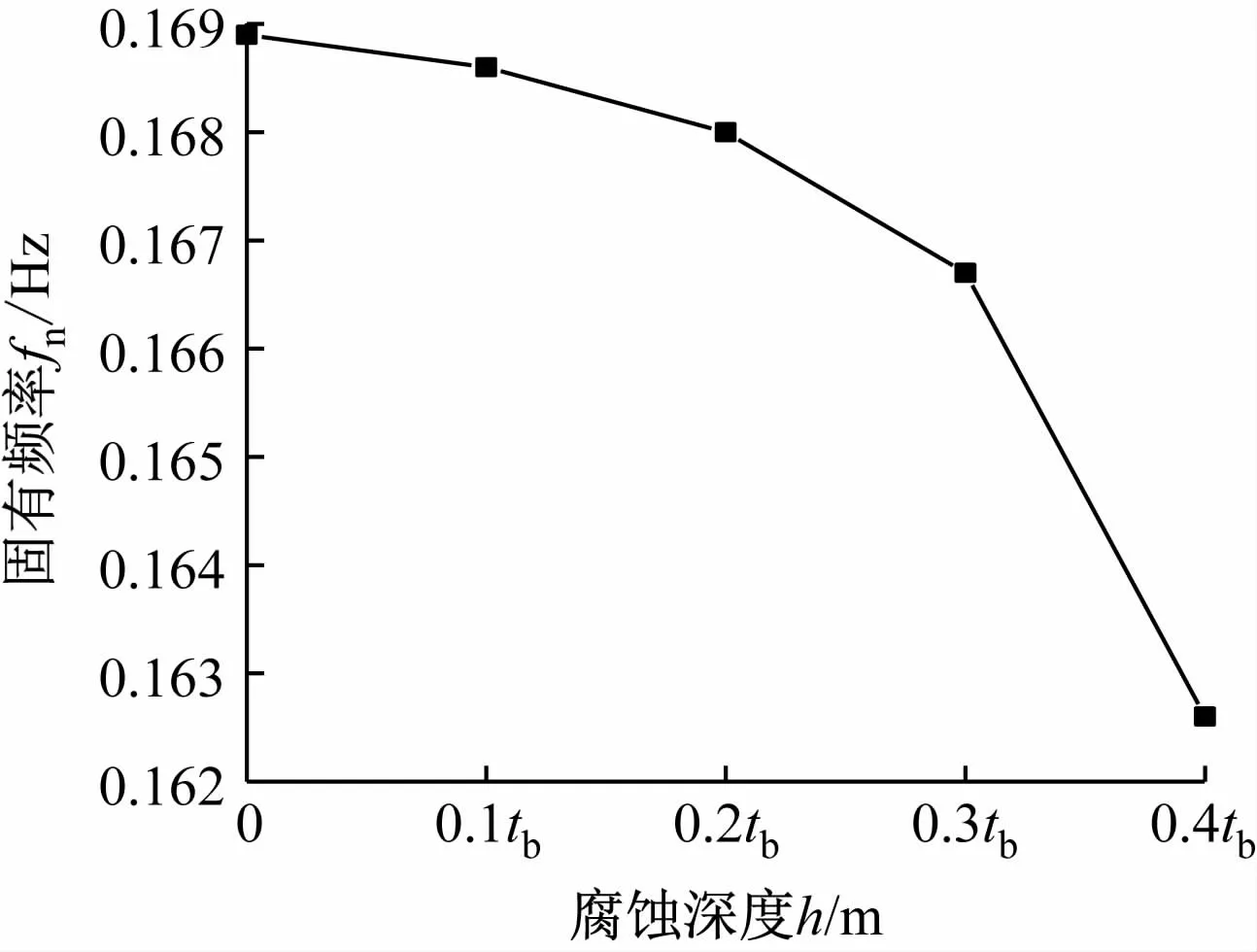
图4 U ＝0.3 m／s时不同腐蚀深度下悬跨管道固有频率的变化情况

3.2 管道振动位移响应振幅分析

图5 为0.25 m／s≤U≤0.50 m／s时不同腐蚀深度下悬跨管道跨中的位移时程，图6 展示了不同海流速度下腐蚀深度对悬跨管道跨中最大无量纲位移振幅的影响。从图5 和图6 中可看出：

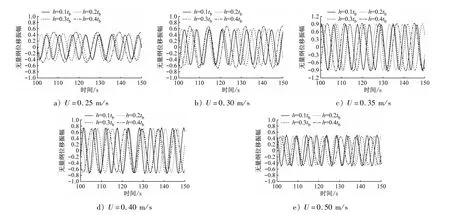
图5 不同海流速度下含腐蚀缺陷的悬跨管道跨中的无量纲位移振幅曲线

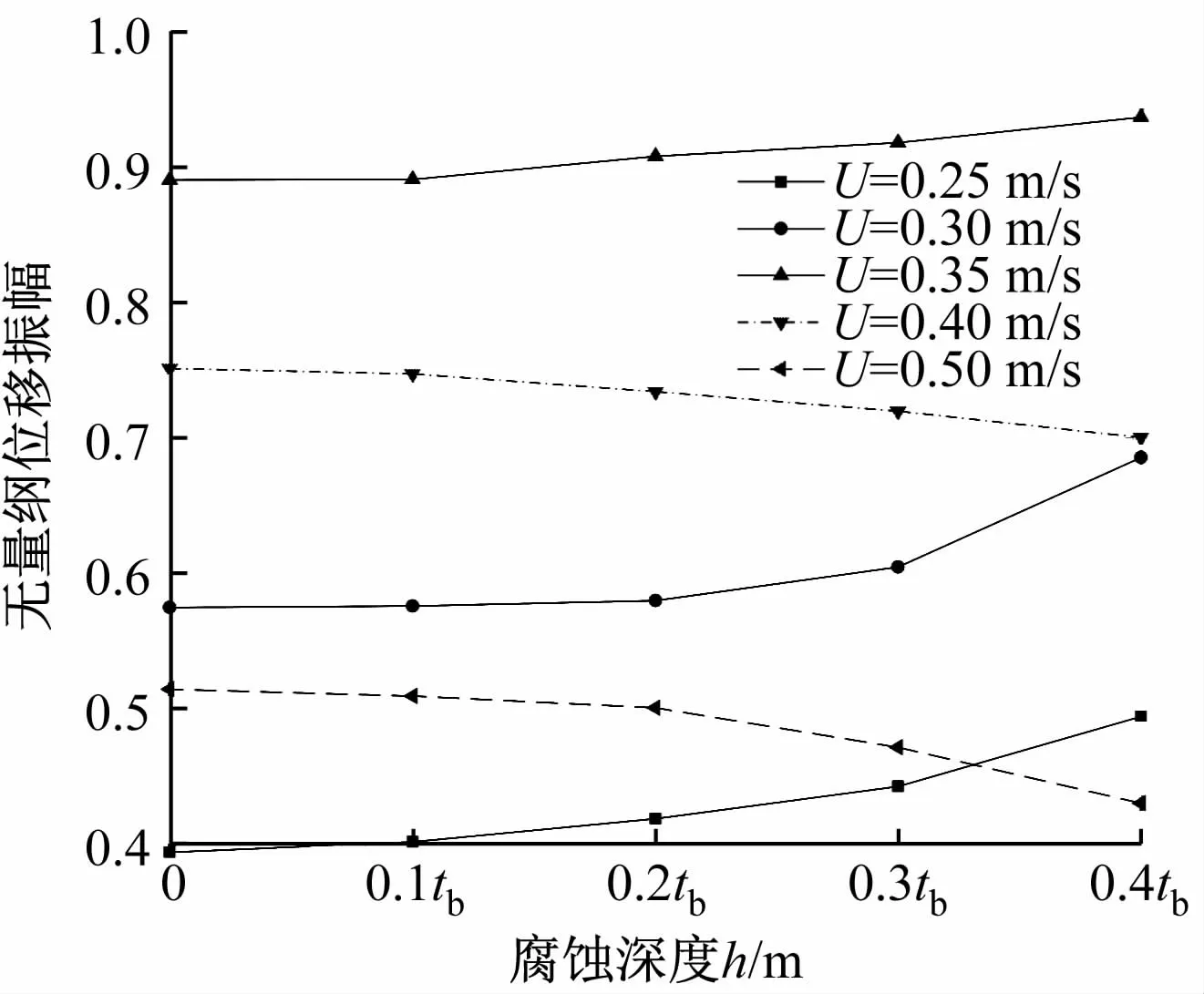
图6 腐蚀深度与悬跨管道跨中的位移响应最大幅值的关系曲线

1）当海流速度一定时，腐蚀深度越大，管道的振动频率越小；当腐蚀深度一定时，海流速度越大，管道的振动频率越大。

2）随着海流速度的增加，管道的腐蚀深度越大，位移响应振幅越大，说明当海底悬跨管道存在腐蚀缺陷时，涡激振动响应加剧。当海流速度增加到一定数值时，管道的位移振幅随着腐蚀深度的增加而减小，说明此时管道的腐蚀缺陷会抑制其振动响应，这是因为涡激振动出现了“频率锁定”现象，与文献［22］的研究结果相同。

3.3 管道应力响应分析

选取海流速度U ＝0.30 m／s、0.35 m／s和0.50 m／s，对不同腐蚀深度下悬跨管道跨中的应力响应进行分析，结果见图7。从图7 中可看出：腐蚀管道发生涡激振动时产生的应力响应大于无腐蚀管道；随着腐蚀深度的增加，跨中的应力逐渐增大，且变化率呈上升趋势，管道的安全性和耐久度下降，对海底管道的安全运行造成威胁。

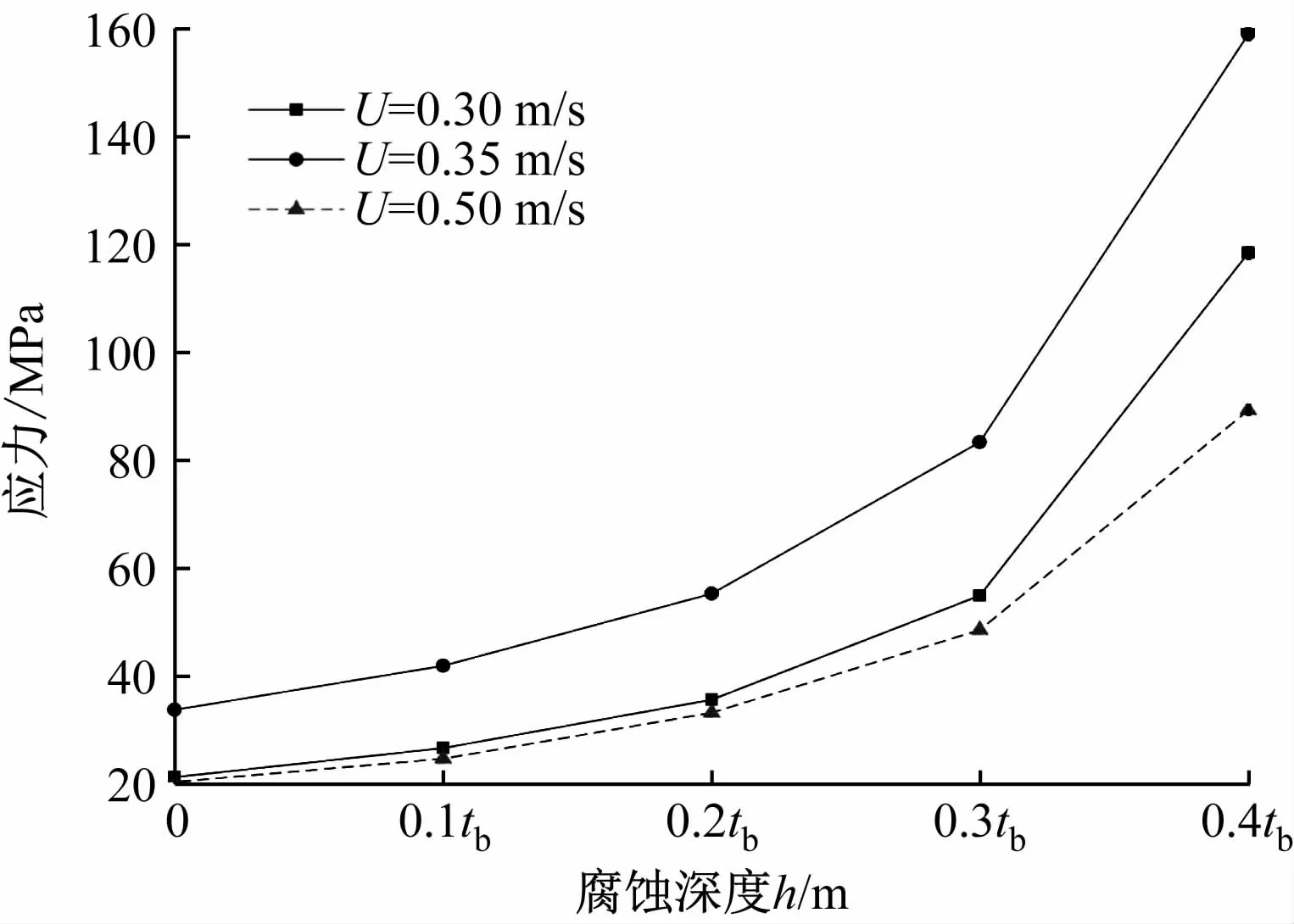
图7 腐蚀深度与悬跨管道跨中的应力响应关系曲线

4 结 语

本文基于Euler-Bernoulli 梁理论和改进范德波尔方程研究了腐蚀条件下海底悬跨管道的涡激振动响应特性，主要得到以下结论：

1）根据含腐蚀缺陷的管道涡激振动模型计算得到的位移数据与有限元模拟结果基本吻合，理论上证实了将悬跨管道简化为梁分析是可行的，为有效预报海底悬跨管道在腐蚀条件下的涡激振动提供了有效的理论计算方法。

2）当发生涡激振动时，随着腐蚀深度的增加，管道的振动频率下降，振动位移更快进入频率锁定区对悬跨管道造成疲劳破坏。因此，在设计海底管道过程中，不能忽视腐蚀缺陷对管道悬跨段的涡激振动的影响。

3）当海流速度小于“频率锁定”的流速范围时，腐蚀缺陷加剧悬跨管道的位移响应，反之抑制悬跨管道的涡激振动。为避免腐蚀缺陷加快涡激振动导致的管道疲劳破坏，应注意加强对管道的腐蚀防护，提升其稳定性。