黏弹性基体中FG-CNTRCs 圆柱壳热振动特性分析

吴栋 ，雷勇军 ，于宝石 ，唐雨 ，张大鹏 †

（1.国防科技大学 空天科学学院，湖南 长沙 410073；2.空天任务智能规划与仿真湖南省重点实验室，湖南 长沙 410073）

碳纳米管（Carbon Nanotubes，CNTs）具有卓越的性能，将CNTs 作为增强体填充到基体中制成复合材料，可将微纳米尺度下CNTs 的优异性能保留到宏观尺度［1］，提高复合材料综合力学性能.CNTs 增强复合材料（Carbon Nanotubes Reinforced Composites，CNTRCs）在航空航天、高速列车和隐身结构等领域展现出广阔应用前景［2］.开展CNTRCs 结构的力学行为研究有助于理解力学特性，指导并促进其在工业中的应用.

开展CNTRCs 结构力学行为研究的方法有实验方法、分子仿真方法（分子动力学或分子力学）和理论方法.其中，实验方法耗时长、成本高，分子仿真方法受限于研究对象的尺寸［3］，因此，采用理论方法研究CNTRCs 结构的力学行为显得尤为必要.而获得CNTRCs的等效材料参数是开展理论研究的基础，目前广泛采用的理论主要有［4］：扩展的混合法则和Eshelby-Mori-Tanaka（EMT）方法.Shen［5］在前人研究的基础上，通过匹配CNTRCs 弹性模量理论计算结果和分子动力学仿真结果，从而将CNTs 效率参数引入经典的混合法则，形成扩展的混合法则.该方法相对简便，但其局限性是无法考虑CNTs 的固有特性，如CNTs的尺度效应.最初，EMT方法被应用于预估含有宏观尺度夹杂相复合材料的等效力学参数，Odegard 等［6］创新性地将EMT 方法运用于纳米复合材料的力学特性分析中，获得了CNTRCs 的等效性能参数，并与实验结果进行对比，验证了所提方法的正确性.EMT方法在高CNTs体积分数时仍有较高的精度［7］，且可在理论模型中考虑CNTs 的固有特性，因此国内外学者广泛采用EMT 方法得到CNTRCs 的等效材料参数，基于连续介质力学理论研究CNTRCs结构的力学行为.

实验发现［8］，微纳米尺度下结构力学特性和宏观尺度下表现出较大差异，产生这种差异的原因是微纳米尺度下结构存在尺度效应.为了突破经典的连续介质力学理论无法考虑微纳米结构尺度效应的局限性，学者们提出了非局部理论、应变梯度理论和偶应力理论等，其中非局部理论与分子动力学和原子晶格动力学的仿真结果吻合较好［9-10］，在CNTs 的力学行为研究中取得了丰硕成果［11-13］.当CNTRCs结构达到微纳米尺度时，同样存在尺度效应.国内外学者们还采用EMT 方法获得微/纳米尺度下CNTRCs结构的等效力学性能参数，基于非局部理论研究了微/纳米尺度下CNTRCs结构的力学行为［14-15］.

20 世纪末，学者们就已经通过实验证实了增强体的尺度下降同样会对复合材料的性能产生影响［16-17］，但目前在CNTs 的尺度效应对CNTRCs 结构力学行为的影响方面的研究有所欠缺，因此，有必要考虑CNTs 尺度效应建立CNTRCs 结构的力学特性研究的理论模型.可设计性是复合材料相对传统材料的显著优势之一，研究不同CNTs 体积分数及其沿特定方向不同分布方式有益于理解CNTRCs 结构的特点，为设计合适CNTRCs 结构形式奠定理论基础.此外，实际工程中CNTRCs 结构工作在复杂环境中，如置于减振的黏弹性基体以及环境温度剧烈变化中.综上所述，研究复杂环境中FG-CNTRCs 结构的力学行为亟须考虑CNTs 的尺度效应时，为其设计和应用提供理论依据.

基于以上考虑，本文以黏弹性基体中的FGCNTRCs 薄圆柱壳为研究对象.首先，基于EMT 方法并考虑CNTs 的尺度效应和取向，建立CNTRCs 的非局部EMT 本构模型.在此基础上，采用Hamilton 原理推导visco-Pasternak 黏弹性基体中FG-CNTRCs Kirchhoff-Love 圆柱壳的热自由振动控制方程，求得两端简支边界条件下固有频率的半解析解，并与文献对比验证其正确性.最后，分析非局部参数、CNTs体积分数及分布方式、圆柱壳几何尺寸、环境温度和地基参数等对FG-CNTRCs 圆柱壳热自由振动特性的影响.

1 热振动问题建模

1.1 CNTRCs的非局部EMT本构模型

考虑基体中CNTs 的取向，可由概率密度函数p(t1，t2)表征，满足［18］

式中：（t1，t2）为欧拉角.当CNTs在CNTRCs中完全随机取向时，有p(t1，t2)=(2π)-1.

采用非局部理论考虑CNTs 的尺度效应，其表达式为：

式中：e0为CNTs的材料常数非局部参数，可通过实验或分子动力学仿真方法确定［19］；a为CNTs 的内部特征尺寸；∇2为拉普拉斯算子；σnonlocal和σlocal分别为非局部应力和经典连续介质力学理论涉及的局部应力.

经典的EMT 方法忽略了CNTs 的尺度效应，此时，代表性体积单元（Representative Volume Element，RVE）中CNT 的应变εCNT(t1，t2)、局部应力与基体的应力σmatrix之间的关系为：

式中：Cm和Cr分别表示基体和CNTs 的刚度矩阵；AEMT为四阶矩阵［20］.

基于式（2）和式（4）可得，考虑CNTs 尺度效应后RVE 中CNT 的非局部应力和基体应力σmatrix之间的关系为：

假设基体为各向同性线弹性材料且与CNTs 之间完美黏结，有

式中：fm和fr分别表示基体和CNTs 的体积分数，且fm+fr=1.

将式（6）和式（7）代入式（9）和式（10）可得：

式中：Iu表示单位矩阵.

对于式（11），令非局部参数e0a为零即可退化为经典的EMT方法，其刚度矩阵的Voigt记法为：

式中：k、l、m、n、p表示Hill弹性模量.

当CNTs 在基体中完全随机取向时，CNTRCs 可视为各向同性材料，其弹性模量和泊松比的表达式参见文献［18］.

值得注意的是，本节中构建的非局部EMT 模型不仅适用于CNTRCs 的力学特性分析，同样适用于研究一般纳米增强复合材料的力学行为.

1.2 FG-CNTRCs 薄圆柱壳的振动控制方程

图1 为visco-Pasternak 基体中FG-CNTRCs 薄圆柱壳正视图.以圆柱壳中性面边界上一点建立圆柱坐标系（x，θ，z），其中θ轴和z轴方向分别表示圆柱壳的周向和径向；圆柱壳的长度、平均半径和厚度分别为L、R和h；黏弹性地基采用visco-Pasternak 地基模型模拟，其Winkler 弹性模量、剪切模量和阻尼参数分别为kw、ks和cd.

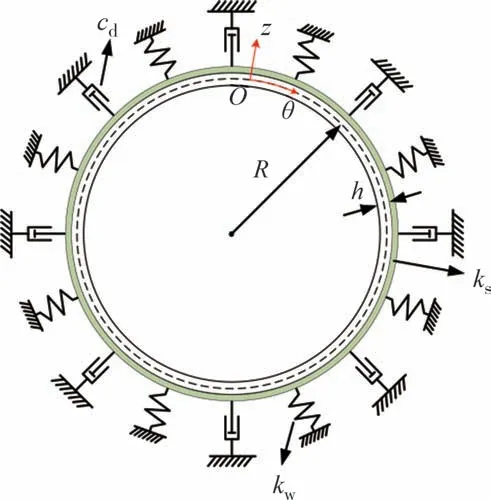
图1 visco-Pasternak基体中FG-CNTRCs薄圆柱壳正视图Fig.1 Front view of thin cylindrical shell of FG-CNTRCs resting on visco-Pasternak foundation

图2 为CNTs 沿圆柱壳厚度方向梯度分布方式，图中圆点在空间竖向分布代表CNTs 沿圆柱壳厚度截面分布量的相对大小，其定量表达式为：

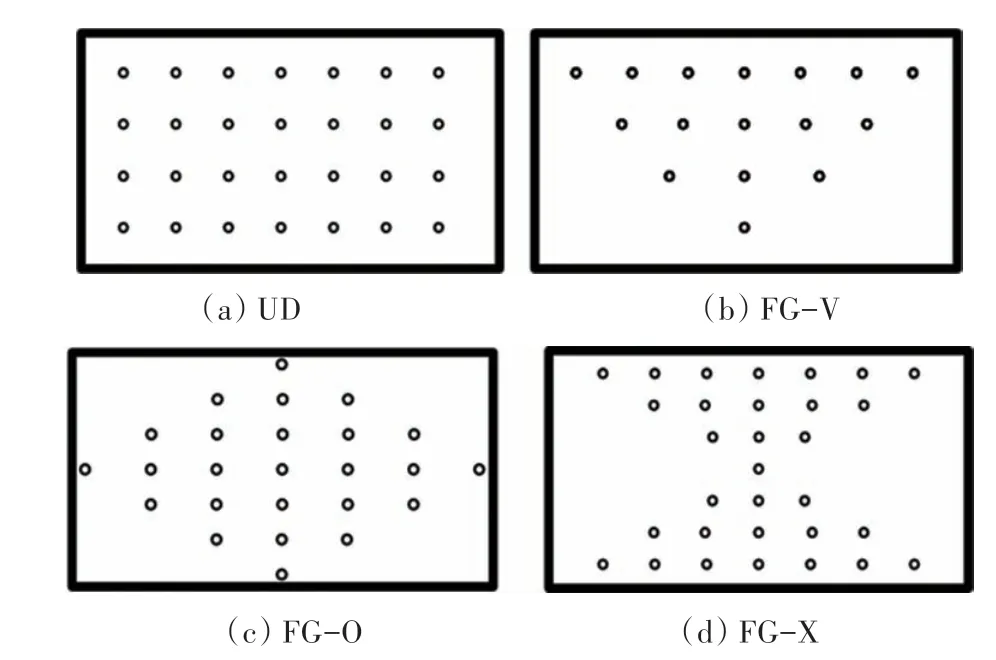
图2 CNTs沿圆柱壳厚度方向梯度分布方式Fig.2 Gradient distribution of CNTs along the thickness direction of the cylindrical shell

式中：UD 表示CNTs 沿圆柱壳厚度截面均匀分布；FG-V、FG-O 和FG-X 分别表示CNTs 沿圆柱壳厚度截面分别为V 型、O 型和X 型（见图2）.显然，不同CNTs分布方式下圆柱壳中CNTs的总体积相同.

FG-CNTRCs 圆柱壳等效材料属性（泊松比和密度等）的表达式为：

基于Kirchhoff-Love薄圆柱壳理论，FG-CNTRCs圆柱壳的位移场为：

式中：（u，v，w）分别表示FG-CNTRCs 圆柱壳上任一点的位移沿（x，θ，z）轴的分量；（u0，v0，w0）分别为圆柱壳中性面上一点位移沿（x，θ，z）轴的分量；t为时间.

根据式（17）、式（18）和式（19），FG-CNTRCs 的应变场为：

将式（20）、式（21）和式（22）代入式（11），进一步考虑热环境的影响，可得：

式中：ΔT为相对室温（300 K）的温度变化；（α11，α22）分别为CNTRCs 沿（x，θ）轴的热膨胀系数.其表达式为［21］：

通过Hamilton 原理获得系统的自由振动控制方程，其表达式为：

式中：δ·表示对变量进行变分运算.

FG-CNTRCs圆柱壳的虚应变能的表达式为：

式中：Θ表示FG-CNTRCs圆柱壳的中性面区域，且

FG-CNTRCs圆柱壳的虚动能δK的表达式为：

外力对FG-CNTRCs做的虚功δW的表达式为：

式中：NQ为visco-Pasternak 地基对FG-CNTRCs 圆柱壳的作用力，（NTx，NTθ）为由环境温度变化ΔT产生的外载荷沿（x，θ）轴的分量，其表达式分别为：

将式（30）、式（33）和式（35）代入式（29），可得系统的自由振动控制方程为：

同时，根据δu0、δv0和δw0在时域和空间域内的任意性可得系统的边界条件为：

式中：（nx，nθ）分别表示单位向量沿（x，θ）轴的方向余弦.设FG-CNTRCs圆柱壳的初始速度和初始位移均为零，即

自由振动控制方程［式（38）、式（39）和式（40）］、边界条件［式（41）～式（45）］和初始条件［式（46）、式（47）］共同构成了visco-Pasternak 基体中FGCNTRCs圆柱壳热自由振动问题的定解条件.

2 方程求解

本文利用Navier法求解简支（Simply-Supported，S-S）FG-CNTRCs 圆柱壳的自由振动固有频率，对于其他边界条件下结构的自由振动固有频率，可通过Galerkin法［22］、Rayleigh-Ritz法［23］等方法进行求解.

S-S边界条件可表示为：

为了便于求解和分析，引入以下无量纲参数：

基于Navier 法，FG-CNTRCs 圆柱壳的位移场可表示为：

式中：（Umn，Vmn，Wmn）分别为振幅沿（x，θ，z）轴的分量；n为周向波数；km=mπ 为轴向波数；Ωmn为FGCNTRCs圆柱壳的无量纲固有圆频率，与有量纲固有圆频率ωmn之间的转换关系为：

将式（49）和式（52）代入式（38）、式（39）和式（40），可将系统的自由振动控制方程改写为：

式中：K3×3、M3×3和C3×3可借助数学软件推导，为保证行文简洁，此处不列出具体的表达式.

对于式（54），FG-CNTRCs的位移场{Umn，Vmn，Wmn}T存在非零解的条件为：

通过求解式（55），可得visco-Pasternak 基体中FG-CNTRCs薄圆柱壳自由振动的无量纲固有频率.

3 结果与讨论

本节首先将模型退化并与文献中报道的结果进行对比，验证所建模型和求解方法的正确性，然后分析非局部参数、CNTs 分布方式与体积分数、环境温度和地基参数等因素对FG-CNTRCs 圆柱壳自由振动无量纲固有频率的影响规律.

如无特别说明，取kw=100 MN/m3，ks=10 MN/m，cd=1×103N·s/m2［24］，且忽略温度对地基材料参数的影响；此外，FG-CNTRCs 圆柱壳的长度L、平均半径R和厚度h分别为1 m、1 m和0.025 m，fr*=5%.基体材料选用聚甲基丙烯酸甲酯（Polymethyl Methacrylate，PMMA），其泊松比νm=0.34，密度ρm=1 150 kg/m3，考虑环境温度对其弹性模量Em和热膨胀系数αm的影响，有［25］

式中：T=T0+ΔT，T0=300 K.根据式（56）和式（57）可知室温下PMMA 的弹性模量Em=2.5 GPa，热膨胀系数αm=4.5×10-5K-1.选取单壁碳纳米管（Single-walled CarbonNanotubes，SWCNTs）作为增强相，泊松比=0.175，密度ρCNT=1400kg/m3，温度相关材料参数为［26］：

式中：P0、P1、P2和P3为常数，对于不同的材料参数，其具体数值如表1所示.

表1 SWCNTs的热机械性能参数Tab.1 Thermo-mechanical properties of SWCNTs

此外，合适的非局部参数可确保分析结果的合理性，可通过将理论结果与实验、分子动力学或多尺度方法分析结果进行匹配确定非局部参数的值［19］.现有结果表明，非局部参数与载荷工况和结构形状等因素相关［27］.目前，国内外学者多采用参数分析的方式研究非局部参数对结构力学行为的影响，如无特别说明，本文取非局部参数α=0.1.

3.1 正确性验证

Loy 等［28］利用广义微分求积法得到了不同边界条件下均匀Kirchhoff-Love 圆柱壳的自由振动特性.当忽略CNTs、visco-Pasternak 地基和热环境的影响（fr*=α=kw=ks=cd=ΔT=0）时，本文所建模型可退化为均匀Kirchhoff-Love 圆柱壳模型.表2 为S-S 边界条件下均匀Kirchhoff-Love 圆柱壳无量纲固有频率的对比结果，其中L/R=20，h/R=0.01，ν=0.3，无量纲固有频率的表达式为：

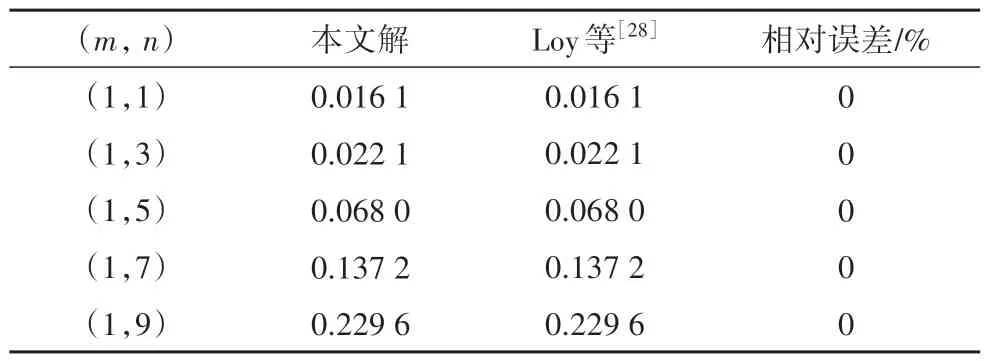
表2 S-S边界条件下均匀Kirchhoff-Love圆柱壳无量纲固有频率的对比结果Tab.2 Comparison of dimensionless natural frequencies of uniform Kirchhoff-Love cylindrical shells under S-S boundary conditions

由表2 可以看出，不同周向波数n下，本文得到的两端简支均匀圆柱壳无量纲固有频率与文献［28］中所列结果均吻合较好.

Loy 等［29］基于Rayleigh-Ritz 法得到了S-S 边界条件下FG Kirchhoff-Love 圆柱壳的振动特性，并进行了参数影响分析.当忽略纳米夹杂的尺度效应、visco-Pasternak 地基和热应变的影响（α=kw=ks=cd=ΔT=0）时，本文所建模型可退化为FG Kirchhoff-Love 圆柱壳模型.圆柱壳的半径R=1 m，λ=20，ξ=0.002，材料参数设置与文献［29］一致.

表3 为S-S 边界条件下FG Kirchhoff-Love 圆柱壳无量纲固有频率的对比结果.由表3 可知，本文求解的简支功能梯度圆柱壳固有频率具有较高的精度；S-S 边界条件下FG 圆柱壳的基频出现在（m，n）=（1，3）处.后续主要分析不同参数对FG-CNTRCs 圆柱壳基频的影响规律.

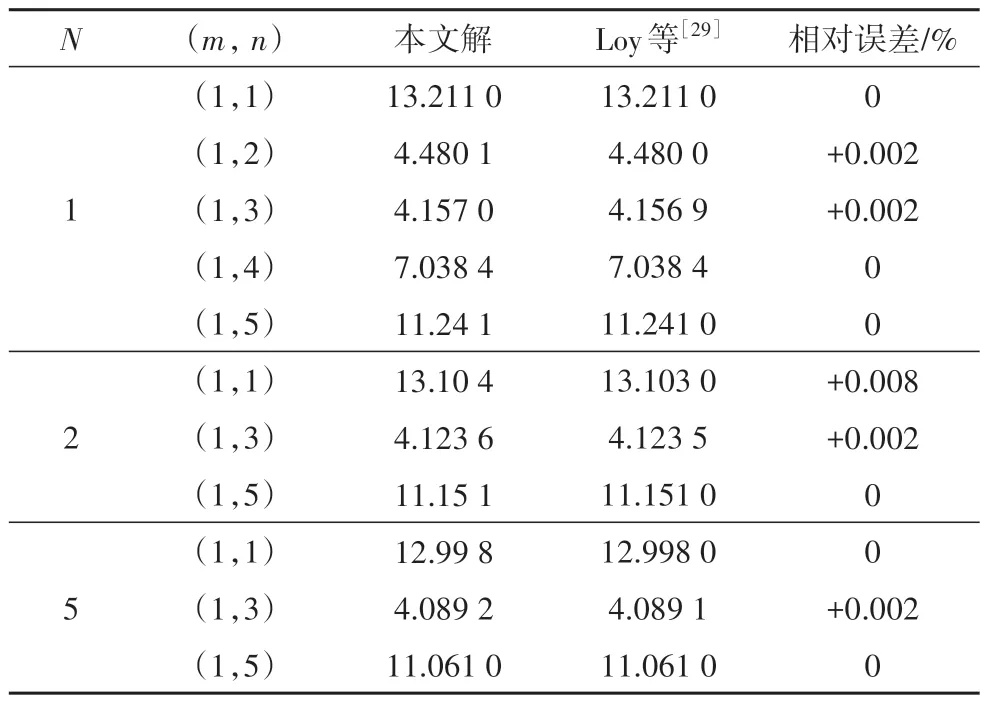
表3 S-S边界条件下FG Kirchhoff-Love圆柱壳无量纲固有频率的对比结果Tab.3 Comparison of dimensionless natural frequencies of FG Kirchhoff-Love cylindrical shells under S-S boundary conditions

3.2 参数影响分析

表4 为不同地基参数和非局部参数下CNTRCs圆柱壳的无量纲固有频率.由表4 可以看出，CNTRCs圆柱壳的无量纲固有频率分为实部和虚部，分别表示系统的阻尼因子和有阻尼固有频率，其中系统稳定的充要条件为固有频率实部为负［30］，且虚部反映了结构的抗弯刚度［31］，因此，本文主要分析各参数对无量纲固有频率虚部的影响规律.非局部参数α对无量纲固有频率实部的影响较小，而虚部随非局部参数α的增大而减小.当非局部参数和地基弹性参数相同时，不同CNTs 分布类型对应的S-S CNTRCs 圆柱壳无量纲固有频率虚部数值按大小排序为：FG-O＜FG-V＜UD＜FG-X，这是由于圆柱壳的内、外径区域是承受正应力的主要区域，而在正应力较大的区域分布更多的CNTs，有利于充分发挥CNTs对复合材料抗弯性能的增强作用.因此，FG-XCNTRCs圆柱壳的无量纲固有频率虚部最大，同时表明了CNTs 在FG-X 分布方式下的抗弯刚度最大.此外，非局部参数对无量纲固有频率虚部的影响幅度随结构抗弯刚度的增大而增大，不同CNTs 分布类型对应的无量纲固有频率虚部减小幅度按大小排序为（kw=ks=0）：FG-O（23.34%）＜ FG-V（23.35%）＜ UD（23.36%）＜ FG-X（23.41%）.

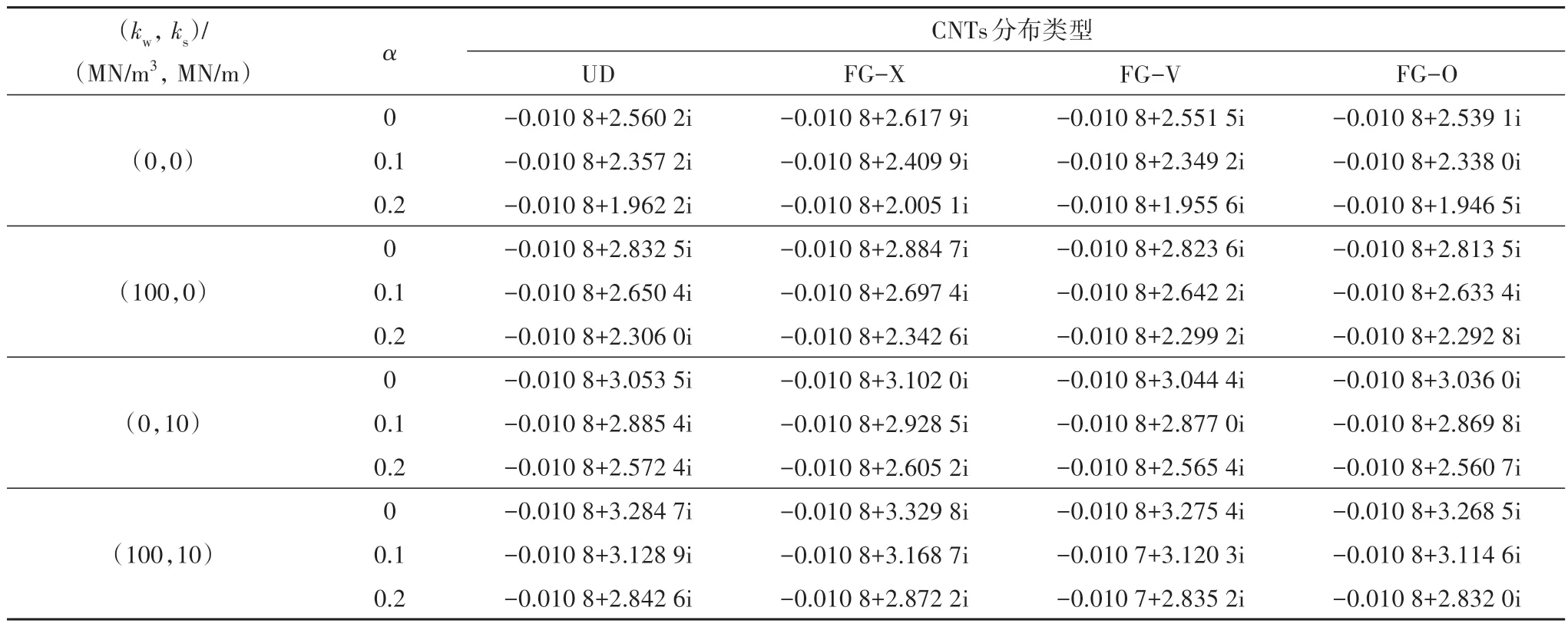
表4 不同地基参数和非局部参数下CNTRCs圆柱壳的无量纲固有频率Tab.4 Dimensionless natural frequencies of CNTRCs cylindrical shell with different foundation parameters and nonlocal parameter

图3 为非局部参数和visco-Pasternak 地基的弹性参数对S-S 边界条件下FG-X-CNTRCs 圆柱壳无量纲固有频率虚部的影响.由图3 可知，无量纲固有频率虚部的减小速度随着非局部参数α的增大而增大.由于visco-Pasternak 地基的弹性参数（kw，ks）增加结构的刚度，因此表4和图3中无量纲固有频率随地基的Winkler 弹性模量和剪切模量的增大而增大.增大visco-Pasternak 地基的弹性参数会降低非局部参数α对CNTRCs 圆柱壳无量纲固有频率虚部的影响幅度，当visco-Pasternak 地基的弹性参数（kw，ks）分别取（0，0），（100，0）和（100，10）时，FG-XCNTRCs圆柱壳无量纲固有频率的下降幅度分别为：23.41%、18.79%和13.74%.此外，当visco-Pasternak地基的剪切模量ks达到一定值时，继续增大其数值对无量纲固有频率虚部的影响幅度较小，此时非局部参数对无量纲固有频率虚部影响幅度的变化也较小.

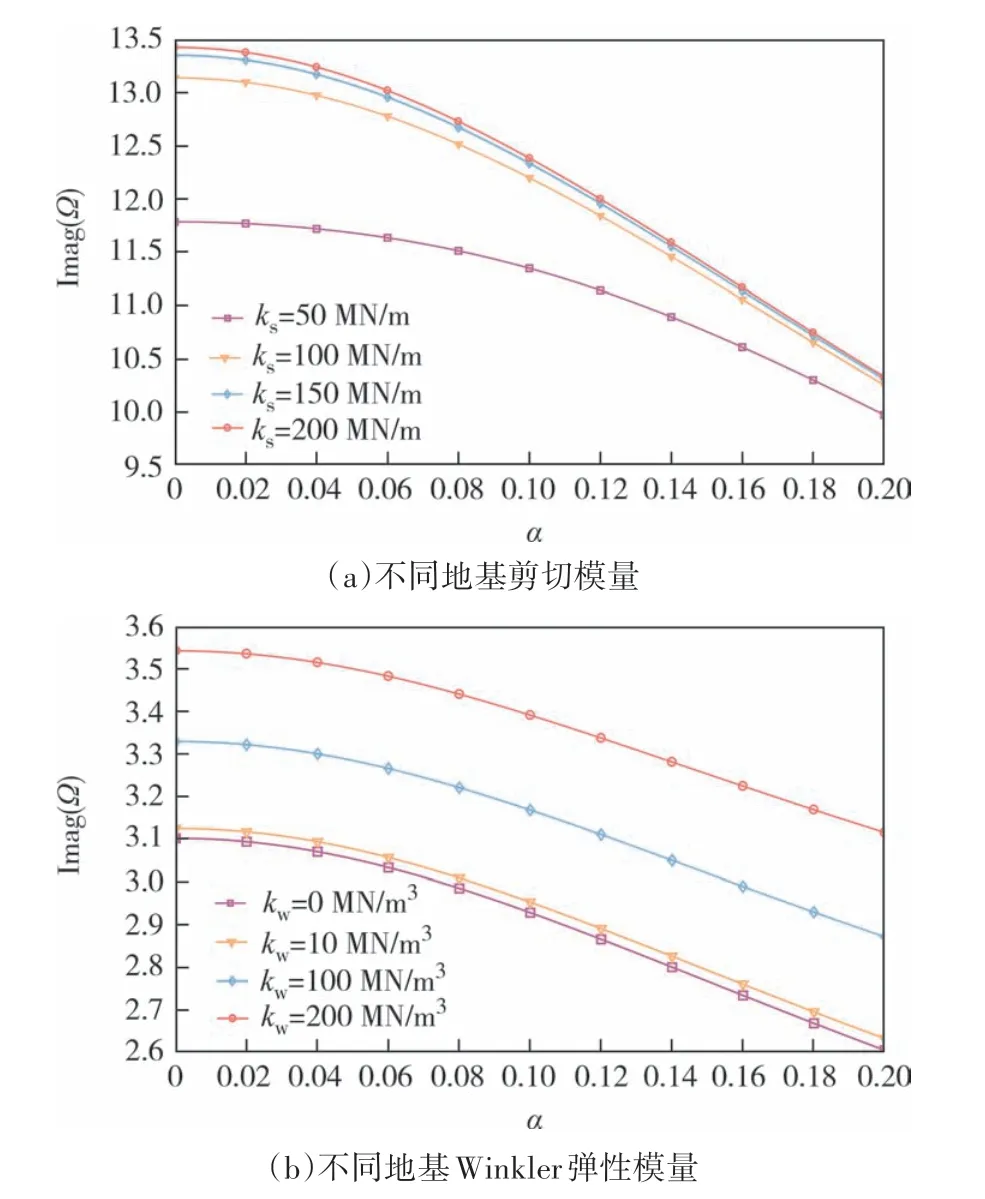
图3 非局部参数对FG-X-CNTRCs圆柱壳无量纲固有频率虚部的影响Fig.3 Effect of nonlocal parameter on the imaginary parts of the dimensionless natural frequencies of FG-X-CNTRCs cylindrical shell

表5 为不同CNTs 体积分数和环境温度下CNTRCs 圆柱壳的无量纲固有频率.由表5 可知，CNTs的体积分数对圆柱壳刚度影响显著，室温（300 K）下FG-X-CNTRCs圆柱壳基体中填充CNTs的体积分数fr*为10.0%时，相对于纯PMMA 基体的无量纲固有频率虚部增加了108.2%，相对于填充CNTs的体积分数fr*为5.0%的虚部增加了53.92%.此外，室温下当CNTRCs 圆柱壳中CNTs 的体积分数fr*由2.5%增至10.0%，不同CNTs 分布类型下无量纲固有频率增大的幅度按大小排序为：UD（51.36%）＜FG-O（52.09%）＜FG-V（52.48%）＜FG-X（53.92%），表明增加CNTRCs圆柱壳中CNTs的含量时，UD-CNTRCs圆柱壳的刚度提升幅度小于FG-CNTRCs 圆柱壳，而3 种CNTs 梯度分布对应的FG-CNTRCs 圆柱壳的刚度提升幅度与结构自身的刚度呈正相关.

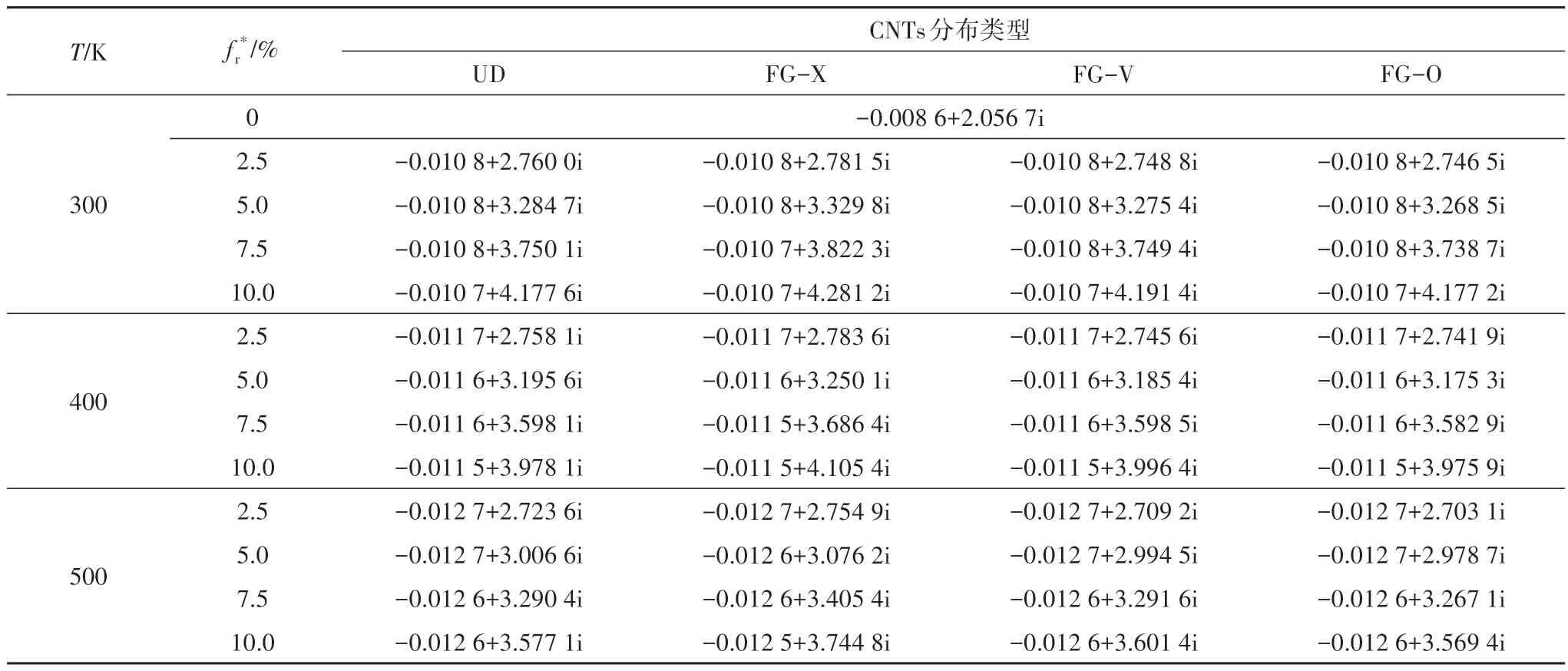
表5 不同CNTs体积分数和环境温度下CNTRCs圆柱壳的无量纲固有频率Tab.5 Dimensionless natural frequencies of CNTRCs cylindrical shell with various values of CNTs volume fraction and ambient temperature

图4 为环境温度对FG-X-CNTRCs 圆柱壳无量纲固有频率虚部的影响.由于增加环境温度导致CNTRCs 圆柱壳结构刚度下降，因此图4 和表5 中无量纲固有频率虚部随环境温度的增大而减小，且减小速度逐渐加快.由图4 可以看出，环境温度对S-S FG-X-CNTRCs 圆柱壳无量纲固有频率虚部的影响幅度随CNTs 体积分数的增大而增大.根据线性理论，FG-CNTRCs 圆柱壳的无量纲固有频率虚部最终会降至零［32］，由图4 可以推断出，无量纲固有频率虚部为零所对应的最小环境温度随CNTs 体积分数的增大而减小.

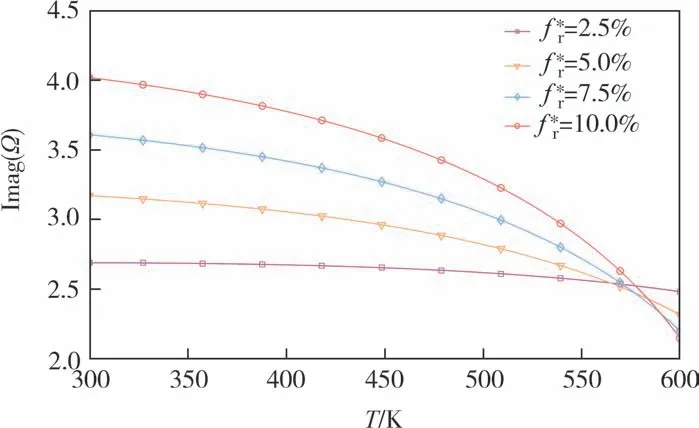
图4 环境温度对FG-X-CNTRCs圆柱壳无量纲固有频率虚部的影响Fig.4 Effect of ambient temperatures on the imaginary parts of the dimensionless natural frequencies of FG-X-CNTRCs cylindrical shell

图5 为长厚比（η-1）对FG-X-CNTRCs 圆柱壳无量纲固有频率虚部的影响，其中=1×103N·s/m2.由图5 可以看出，visco-Pasternak 地基的阻尼系数和长厚比对无量纲固有频率虚部的影响有耦合作用，当地基的阻尼系数较小时，无量纲固有频率虚部随长厚比的增大先增后减；增大地基的阻尼系数后，无量纲固有频率虚部随长厚比的增大而减小，最终减至零，减小的速度逐渐增加，无量纲固有频率虚部减为零说明该长厚比和阻尼系数组合所构成的系统处于过阻尼状态.此外，增加visco-Pasternak 地基的阻尼系数会降低系统无量纲固有频率虚部为零对应的最小长厚比.

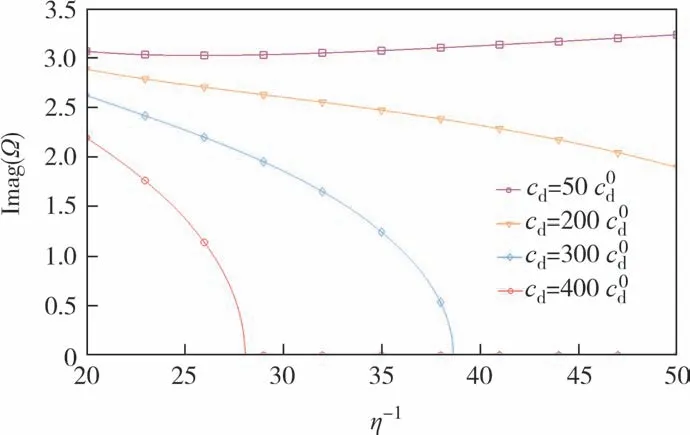
图5 长厚比（η-1）对FG-X-CNTRCs圆柱壳无量纲固有频率虚部的影响Fig.5 Effect of length-thickness ratio（η-1）on the imaginary parts of the dimensionless natural frequencies of FG-X-CNTRCs cylindrical shell

4 结论

本文基于EMT 方法并考虑CNTs 的尺度效应和取向建立CNTRCs 力学特性分析的非局部EMT 本构模型.在此基础上建立visco-Pasternak 基体中FGCNTRCs Kirchhoff-Love 圆柱壳的热自由振动控制方程，并得到两端简支边界条件下结构的固有频率.主要结论如下：

1）考虑CNTs 的尺度效应会降低FG-CNTRCs 圆柱壳的抗弯刚度，非局部参数对无量纲固有频率虚部的影响幅度随结构刚度的增大而增大.

2）增加CNTs 的含量时，UD-CNTRCs 圆柱壳刚度提升幅度小于3 种FG-CNTRCs 圆柱壳，且环境温度对无量纲固有频率虚部的影响随CNTs 体积分数的增大而增大.

3）长厚比和visco-Pasternak 地基的阻尼系数对无量纲固有频率虚部的影响有耦合作用.