广西钦崇高速公路膨胀土动力变形及动强度特性试验研究

唐咸远,王诗海,马杰灵,罗 杰

(1. 桂林电子科技大学 建筑与交通工程学院,广西 桂林 541004;2. 广西科技大学 土木建筑工程学院,广西 柳州 545006;3. 广西北投交通养护科技集团有限公司,广西 南宁 530029)

0 引 言

膨胀土在我国分布范围较广,具有胀缩和裂隙发育等特性,对工程建设的危害大、损失重、防治难。随着我国交通基础建设的加快,高速公路、铁路必然会穿越更多的膨胀土分布区,因车辆荷载的影响,路基沉降变形和开裂问题也越来越突出[1]。因此,开展膨胀土的动力特性研究,对路基状态评估和沉降变形分析具有重要实践意义。

目前,国内外学者在土体动力特性方面的研究较多[2-5]。对于累积变形的研究,庄心善等[6]得出,合肥弱膨胀土累积变形特征在正弦波加载条件下符合单对数模型曲线的发展规律;梅慧浩等[7]采用正弦波加载方式建立了路基粗粒土的永久变形预测模型,并给出模型参数取值范围;L.TANG等[8]对路基填料进行单级和多级循环荷载试验,得出了长期低动应力荷载下的累积应变经验模型;LI Jian等[9]研究了不同动应力和围压等因素对重塑红黏土作为路基填料时累积变形的影响;商拥辉等[10]通过数值模拟和室内试验,得出了不同动应力幅值下水泥改良膨胀土路基累积变形经验模型。在滞回曲线的研究方面,庄心善等[11]研究了围压和动应力幅值对风化砂改良膨胀土滞回曲线特征的影响;魏新江等[12]研究了不同温度和固结度对冻融土滞回曲线特征变化的影响;黄娟等[13]分析了泥炭质土在分级加载下围压和固结比对滞回曲线演化影响。在动强度特性的研究方面,匡月青等[14]对饱和软黏土开展动三轴试验,研究了土体在列车荷载作用下的动强度特性;WANG Min等[15]得出了改良膨胀土在不同含水率下的动强度参数;冷伍明等[16]分析了不同围压和动应力幅值对粗粒土作为路基填料时的动强度影响。综上所述,大部分学者在土体累积变形、滞回曲线及动强度特性的研究上均取得了一定成果,研究对象主要集中在粗粒土和黏土之间,且采用的加载波形多以正弦波为主。但孙阳光等[17]、李金秋等[18]研究表明,交通循环荷载更接近于半正弦波形,故在膨胀土的动力特性研究中采用半正弦波加载比采用正弦波加载更为合理,而目前关于半正弦波加载下的膨胀土累积变形及动强度特性方面的研究却鲜有报道。

基于此,笔者选取广西钦崇高速公路膨胀土为研究对象,开展了半正弦波加载条件下的室内GDS动三轴试验,分析了膨胀土在半正弦波加载条件下不同围压σ3c和动应力σd对土体累积变形、滞回曲线特征变化和动强度特性的影响,并建立了累积变形预测模型、动强度衰减公式以及黏聚力和内摩擦角随破坏振次变化的归一化公式,试验结果可为膨胀土地区的路基变形及沉降分析提供参考。

1 试验研究方法

1.1 试验仪器

采用英国GDS高级动态三轴测试系统,最大可施加10 kN轴向荷载和5 Hz频率,通过更换不同尺寸底座及传感器可对不同直径大小的试样进行试验。试验过程中由电脑实时采集围压、反压、轴向应变及轴向荷载等数据,内置的模块可对土体进行饱和度及反压饱和度检测,满足试验各项需求。

1.2 试验土样

试验用膨胀土取自广西防城港上思县钦崇高速公路K59+300深1.5～2.0 m处,为条纹状(灰白、紫红、黄色条纹)风化泥岩,呈硬塑-坚硬状;膨胀土最大干密度为1.84 g/cm3,最优含水率为16.89%,自由膨胀率为53.5%。根据JTG/ C20—2011《公路工程地质勘察规范》和TB 10012—2019《铁路工程地质勘察规范》,试验用膨胀土可划分为弱膨胀土,其基本物理性质指标如表1。试样为50 mm(直径)×100 mm(高)的圆柱形重塑土样,按最优含水率及最大干密度计算配置成湿土。采用静压法分4层制样,每一层均进行刨毛处理,制样严格按照JTG 3430—2020《公路土工试验规程》进行,要求配置的湿土含水率误差和干密度误差分别在 ±1%和 ±0.02 g/cm3以内。

表1 膨胀土基本物理性质指标

1.3 试验方案

试验过程分为饱和、固结及振动3个阶段。试验开始前,采用真空饱和器对制成试样进行抽气注水饱和,再将试样装入GDS动三轴系统上的压力室内进行反压饱和,当饱和度0.96时,即可认为试样已达到饱和;固结阶段采用等向固结,即固结比kc=1,加载波形选用半正弦波(加载方式如图1),对土体进行单一幅值下的固结不排水三轴试验。每个试样振动10 000次,当轴向累积应变达到5%,视为土样已破坏。公路路基压实标准一般要求在90% 以上,本次试验试样压实度控制在94%,加载频率为1 Hz,围压σ3c选取50、100、150 kPa,试验方案如表2。

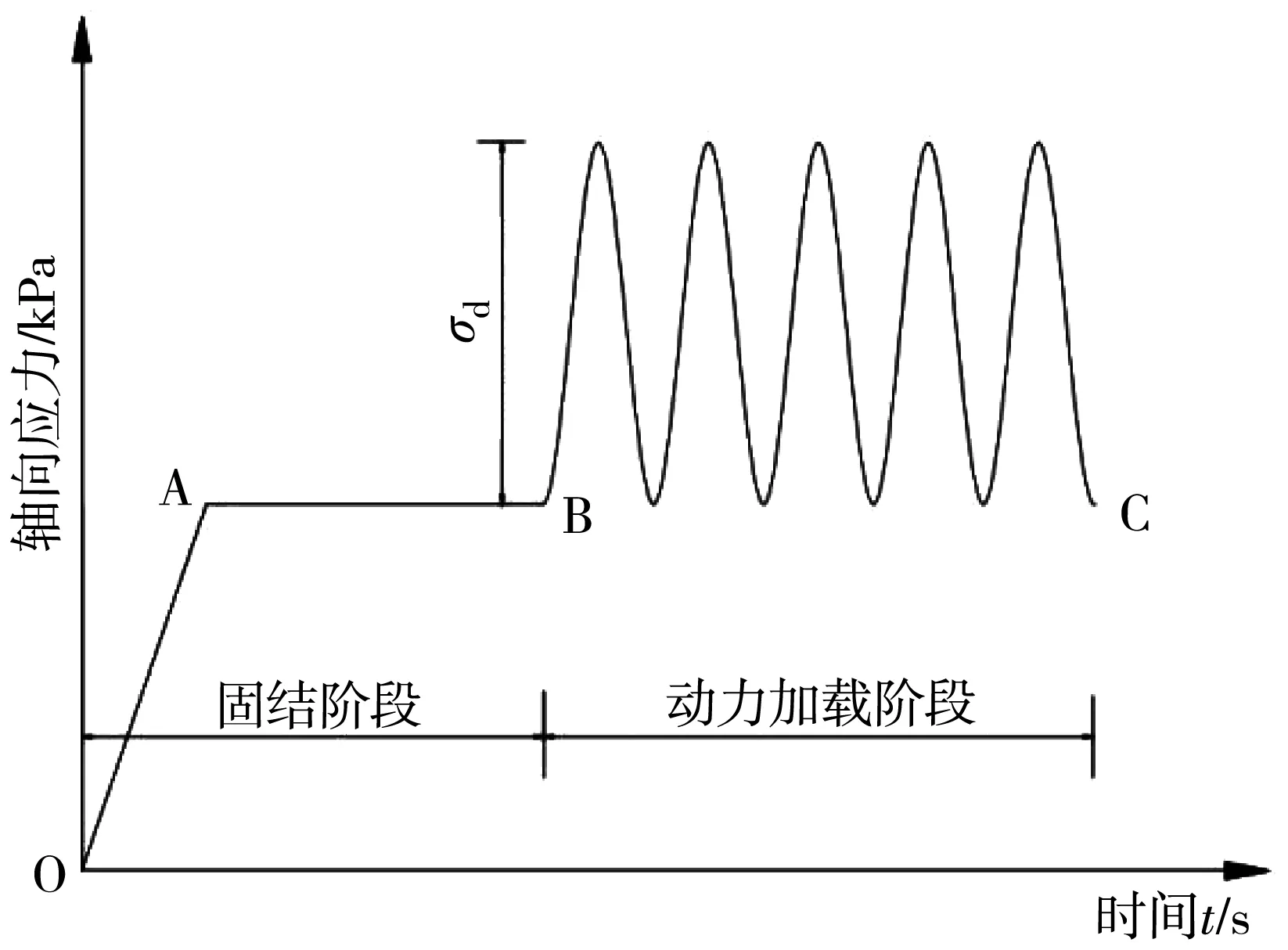
图1 半正弦波加载过程Fig.1 Half-sine wave loading process

表2 试验方案

2 试验结果分析

2.1 累积变形分析

通过对试验数据的处理,在半对数坐标下绘制了不同围压膨胀土轴向累积应变与振次之间的关系曲线(图2)。由图2可知,随着动应力的不断增加,膨胀土的累积变形逐渐增大,围压50、100、150 kPa下的膨胀土在动应力小于75 kPa时均没有发生破坏,而是呈稳定型的变化发展趋势;动应力小于75 kPa时,膨胀土的累积变形在初期发展较快,处于应变快速增长阶段,随振动次数的持续增加,土体内部孔隙不断被压缩减小,导致土体密实度逐渐增大,颗粒间的相对滑移变得困难,经过1 500次的振动加载后累积变形逐渐趋于稳定,此时处于应变稳定阶段。

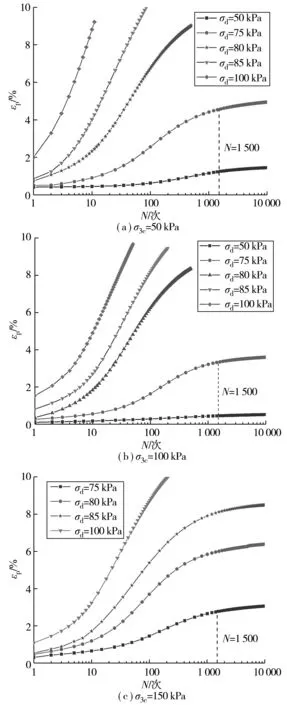
图2 不同围压下轴向累积应变εp与振次N之间的关系Fig.2 The relationship between axial cumulative strain and vibration times under different confining pressure

以围压50 kPa、动应力50 kPa为例,振动至1 500次时,相对于第1次振动,累积应变增长了66.9%;振动至1 500～10 000次时,累积应变只增长了14.4%。由此可见,膨胀土的累积变形主要发生在应变快速增长阶段,当动应力大于80 kPa时,土体累积变形在较短时间内迅速增大直至土体被破坏,呈破坏型的变化发展趋势。试样破坏前后情况如图3。由图3可知,试样为中部鼓胀破坏。当荷载超过土体骨架结构屈服应力一定值后,结构瞬间发生破坏,土颗粒间迁移幅度变大,变形加快,从而发生了破坏。

图3 试样破坏前后Fig.3 Before and after the sample failure

2.2 累积变形预测模型

目前,常用于描述土体轴向累积应变与振次之间关系的模型有双曲线模型[19]、Monismith幂函数模型[20]、单对数模型[6]等,分别如式(1)～式(3):

(1)

εp=ANb

(2)

εp=α+βlgN

(3)

式中:εp为轴向累积应变;N为振次;α、β、A、b均为与土体相关的拟合参数。

以σ3c=100 kPa,σd=75 kPa为例,采用式(1)、式(2)、式(3)共3种模型对膨胀土的轴向累积应变与振次之间的关系进行拟合,如图4。由拟合结果可知:双曲线模型和单对数模型的决定系数R2均比Monismith幂函数模型要高,双曲线模型更贴近于试验点,但还是存在一定的偏差;单对数模型不能从原点开始拟合,即N只能从1开始取值;在轴向累积应变发展阶段和过渡至稳定阶段的曲线拐点处(图4中箭头所示区域),单对数模型和Monismith幂函数模型的拟合值相比于实测值偏差均较大。因此,采用上述3种模型均不能很好地描述出膨胀土累积变形发展趋势。

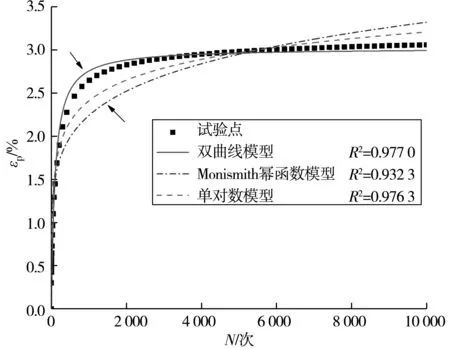
图4 不同模型拟合效果对比Fig.4 Comparison of fitting effects of different models

基于此,考虑膨胀土的累积变形发展特点,参照双曲线模型,对膨胀土的轴向累积变形曲线进行修正,建立一个考虑稳定型和破坏型发展趋势的累积变形预测模型,如式(4):

(4)

式中:a、B、m均为与土体围压、动应力等相关的拟合参数。当N趋于无穷大且处于稳定型增长阶段时,轴向累积应变取得最大值,即εp=1/B。该模型是在试验围压为50～150 kPa、动应力为50～100 kPa、加载频率为1 Hz、固结比为1.0条件下所得。

现仍以动应力σd=75 kPa为例,绘制不同围压下轴向累积应变与振次之间的关系拟合曲线(图5),拟合参数见表3。从图5和表3的拟合结果可知,预测模型的决定系数均较高,最小值为0.994 7,平均值约为0.996 1,均比双曲线模型、Monismith幂函数模型和单对数模型的决定系数要高,且新模型拟合曲线更贴近于试验点,表明新模型能较好地描述膨胀土累积变形发展趋势。

图5 不同围压轴向累积应变与振次关系拟合Fig.5 Relationship fitting between axial cumulative strain and vibration times under different confining pressure

表3 轴向累积应变与振次拟合参数

根据表3得到的拟合参数a、B、m,可判别试样所处的状态。对于参数a而言,当a=3.621 6时,试样处于稳定状态;当a<3.621 6时,试样发生了破坏;当a>3.621 6时,试样处于稳定状态,其中,当a=4.185 1时,试样却处于破坏状态。因此,当a∈(3.621 6,4.185 1)时,将此区间作为试样的临界破坏区间;当a>4.1851时,试样处于稳定状态。对于参数B而言,当B≥0.194时,试样处于稳定状态;当B<0.194时,试样发生了破坏。对于参数m而言,当m≤0.698 6时,试样处于稳定状态;当m>0.698 6时,试样处于破坏状态;而当m=0.789 8时,试样却处于稳定状态;当m>0.789 8时,试样处于破坏状态。因此,将m∈(0.698 6,0.789 8)作为试样临界破坏区间。

2.3 滞回曲线特性分析

滞回曲线反映了土体在动荷载作用下的动变形和耗能特性,开展滞回曲线的探讨对土体动本构模型和抗震性能研究具有重要意义[21]。

2.3.1 不同振次下滞回曲线演化规律

为研究不同振次下滞回曲线的变化规律,以累积变形呈稳定型发展趋势的膨胀土为例,取σd=75 kPa,绘制在不同围压、不同振次下经处理后的滞回曲线(图6)。图6中,εd为动应变。由图6可知,滞回曲线的倾斜程度和面积随振次的不断增加而减小,围压50、100、150 kPa下的滞回曲线均是由稀疏到紧密的变化过程,这也反映了土体在动应力下逐渐被压密实的过程。在振次小于100次时,不同围压下的滞回曲线均比较饱满和宽厚,说明土体初期的刚度较强,能吸收施加在土体上的大部分能量,具有良好的抗震性能和耗能能力;同一围压下,随振动次数的不断增加,滞回曲线的形状逐渐发生变化,由早期的饱满梭形逐渐变为窄扁的柳絮条状,反映了土体的刚度和耗能能力在连续振动加载下逐渐发生退化和降低,土体的累积变形逐渐增大,直至出现稳定或发生破坏。

2.3.2 不同围压下滞回曲线演化规律

为探讨不同围压下膨胀土的滞回曲线变化规律,现以σd=75 kPa为例,绘制不同围压下第100、1 000、10 000次振动的滞回曲线(图7)。

由图7可知,在不同围压同一振次下的滞回曲线面积各不相同,面积越大,土体损耗的能量就越大。N=100次时,围压50 kPa下的滞回曲线面积相比围压100 kPa和150 kPa滞回曲线面积分别大了28.9%和41.1%;N=10 000次时,围压50、100、150 kPa下的滞回曲线面积相比N=100次时分别减小了19.1%、17.3%和9.9%。同一动应力下,围压150 kPa下的膨胀土滞回曲线面积衰减最小,同时损耗的能量最少,发生破坏的可能性就越小;相反,围压50 kPa下的膨胀土更易于发生破坏,说明增大围压可以抑制土体的轴向累积变形,有利于提高土体强度和抵抗剪切破坏的能力。随着围压的增加,同一动应力下的滞回曲线斜率逐渐增大,滞回曲线逐渐朝动应力轴方向靠拢,土体产生的动应变逐渐减小。

2.4 动强度特性分析

2.4.1 动强度曲线特性分析

土体动强度是指在一定动荷载循环作用次数下产生某一指定破坏应变或破坏标准所需的动应力值。破坏标准不同,对应的动强度值也不同。根据GB/T 50269—2015《地基动力特性测试规范》,取轴向累积应变达到5%作为破坏应变,绘制不同围压下膨胀土的动强度曲线(图8)。膨胀土的动强度曲线符合幂函数曲线衰减规律,如式(5):

图8 不同围压下膨胀土动强度曲线Fig.8 Dynamic strength curve of expansive soil under different confining pressure

(5)

式中:p、q为与土体相关的拟合参数;Nf为不同动应力对应的破坏振次。

从图8可以看出:不同围压下膨胀土动强度曲线均呈现幂函数形式的衰减规律,决定系数R2均在0.90以上,表明与幂函数存在较强的相关性,由拟合结果可知,动强度曲线p值介于113.7～139.6,q值介于0.094 2～0.142 2;随破坏振次的增加,动强度衰减速率逐渐降低,且呈趋于平缓的趋势,表明减小动应力能提高土体达到破坏所需的次数;围压越大,膨胀土需要的破坏振次就越多,这是因为围压的增大导致土体密实度增加,低振次下要使土体发生破坏就需要更大的动应力,而低动应力下就需要更高的振次才能达到同一破坏条件。

为比较膨胀土动强度和静强度之间的差异变化情况,通过静三轴试验得出破坏应变为5% 时不同围压下的静强度参数(表4)。表4中:σ为静强度值;c0为黏聚力;φ0为内摩擦角。分析图8和表4可知,不同围压下的静强度值一般大于动强度值。因此,在对路基工程设计时不能只按照单一静强度下的参数进行选择,应该结合静强度和动强度综合考虑参数的取值。

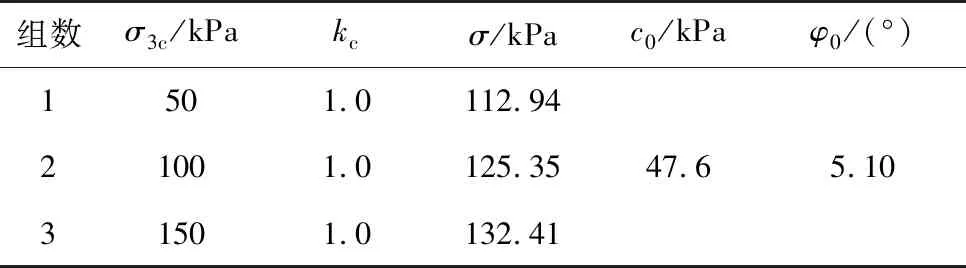
表4 不同围压下静强度参数

2.4.2 动强度指标分析

动强度指标分为动黏聚力cd和动内摩擦角φd,cd和φd是土体的2个重要参数指标[22]。通过图8可求得在不同围压不同振次下的破坏动应力值。根据文献[23] 的计算方法,可求出动强度指标参数,继而绘制莫尔圆。图9为膨胀土的抗剪强度包络线。图9中:动三轴试验得到的强度包络线截距为动黏聚力cd;公切线与x轴夹角为动内摩擦角φd。分别求得cd=35.9 kPa,φd=4.06°。依据此方法可求出膨胀土在其它振次下的cd和φd值。静三轴试验得到的抗剪强度包络线截距为黏聚力c0,公切线与x轴夹角为内摩擦角φ0,分别求得c0=47.6 kPa、φ0=5.10°。从图9可以看出,静三轴试验下的c0和φ0要大于动三轴试验下的cd和φd,这也解释了2.4.1节提到的膨胀土静强度值大于其动强度值。

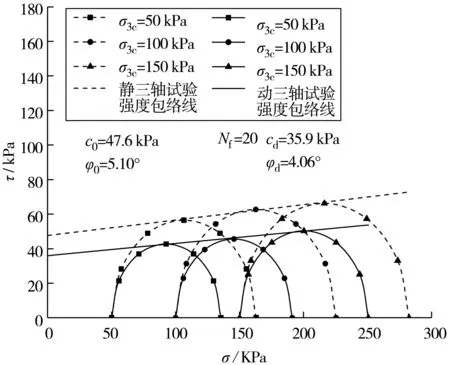
图9 抗剪强度包络线Fig.9 Shear strength envelope

绘制cd和φd随不同破坏振次变化曲线(图10)。由图10可知,在半对数坐标下,膨胀土的动黏聚力cd和动内摩擦角φd随lgNf的增加呈线性减小趋势。cd和φd随lgNf变化的线性拟合公式分别如式(6)、式(7):

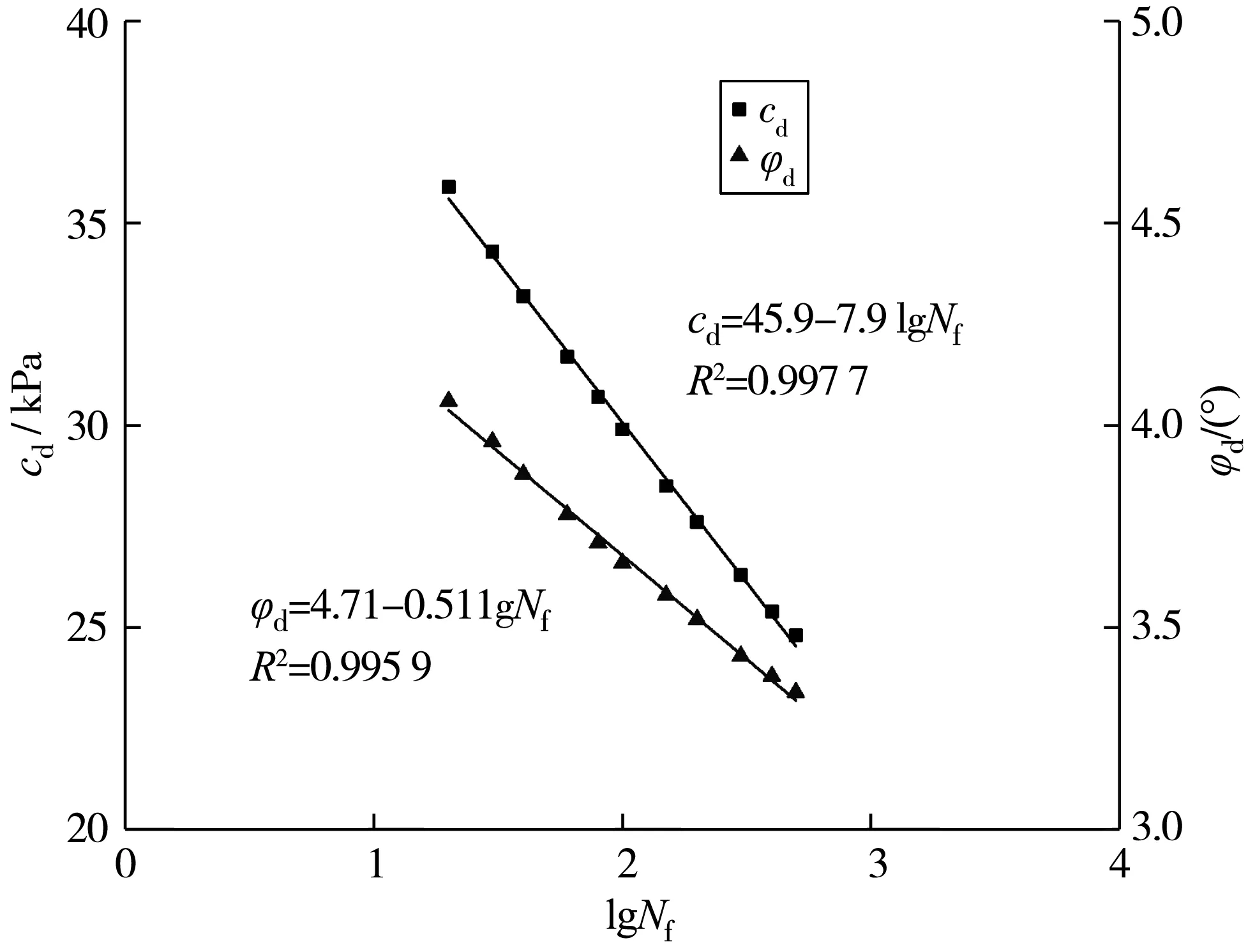
图10 动强度指标与破坏振次之间的关系Fig.10 Relationship between dynamic strength index and failure vibration times

cd=45.9-7.9 lgNf

(6)

φd=4.71-0.51 lgNf

(7)

决定系数R2均大于0.99,且cd随lgNf变化的衰减速度要大于φd的衰减速度,说明cd与土颗粒间的黏结力密切相关,可理解为在循环荷载作用下膨胀土本身密实的骨架颗粒逐渐发生松散和迁移,导致土颗粒间的胶结作用力逐渐降低,随振次的不断增加,土体最终发生变形和破坏。根据拟合公式分别求得破坏振次在第1次至第10 000次之间的cd=14.3～45.9 kPa,φd=2.67°～4.71°。对式(6)和式(7)进行整理后可得出cd与φd之间的关系式也为线性关系,如式(8):

cd=15.6φd-27.1

(8)

由式(8)可知,cd随φd的增加而增大,反之减小。

将不同振次对应的cd和φd分别除以同一破坏应变条件下的静强度指标参数c0和φ0(表4),得到的不同振次下黏聚力和内摩擦角归一化曲线如图11,拟合公式如式(9)、式(10):

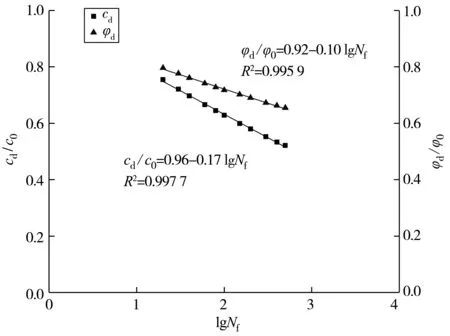
图11 归一化强度指标曲线Fig.11 Normalized strength index curve

cd/c0=0.96-0.17 lgNf

(9)

φd/φ0=0.92-0.10 lgNf

(10)

由图11可知,决定系数R2分别为0.997 7、0.995 9,拟合度较高。

3 结 论

1)膨胀土轴向累积应变随振次变化关系可分为稳定型和破坏型曲线发展规律,动应力较小时为稳定型,反之为破坏型;基于双曲线模型修正的累积变形预测模型能较好地描述膨胀土累积变形特征,并得到了不同围压和动应力下的拟合参数值,可根据拟合参数取值范围判别试样所处的状态。

2)随振次的增加,围压50、100、150 kPa下的膨胀土滞回曲线倾斜程度和面积逐渐减小,形状由饱满梭形变为窄扁的柳絮条状,土体刚度和耗能能力逐渐降低;增大围压,滞回曲线逐渐朝动应力轴方向靠拢,斜率逐渐增大,动应变减小,土体刚度和耗能能力逐渐增加。

3)膨胀土动强度与幂函数曲线存在较强的相关性,随破坏振次的增加,曲线斜率逐渐减小;绘制了破坏振次为20次时的动、静三轴试验下的应力莫尔圆,得到cd=35.9 kPa,φd=4.06°,c0=47.6 kPa,φ0=5.10°;半对数坐标下的动黏聚力cd和动内摩擦角φd均与lgNf呈线性关系,cd减小幅度大于φd减小幅度,给出了cd随φd变化的关系式,得到了强度指标参数随lgNf变化的归一化公式。