钢管混凝土拱肋日照梯度温度效应研究

郭增伟,张亚丽,杨一帆,周水兴

(重庆交通大学 土木工程学院,重庆 400074)

0 引 言

随着对钢管混凝土性能的深入研究,管内混凝土已从最初的防锈功能逐渐转变为同钢管联合承载的结构,并广泛应用到桥梁建设中。自20世纪90年代以来,中国修建的各式钢管混凝土拱桥已超400座[1]。尽管钢管混凝土拱桥发展很快,但作为一种新兴的组合结构,在理论计算方面仍滞后于实践,同时在施工及服役期间的钢管混凝土拱桥由于温度荷载影响,大都存在热脱空现象[2],由此会造成安全问题。

有研究表明,由于温度荷载引起的截面温度应力与结构的自重应力相当[3]时,极易造成结构脱空,大量学者针对温度荷载对结构的影响做了研究。颉志强等[4]通过现场试验与精细化仿真分析相结合的方法,对西藏高海拔地区的水工混凝土结构在日照下的温度分布不均匀性进行了计算与模拟,给出了提高结构受照模拟效率的快速算法,并开发了计算程序;韩辉等[5]以合阳嘉陵江大桥钢管混凝土拱桥为研究对象,比较分析了该桥实测变形与理论温差计算变形间的差异及原因,指出温度对拱桥线形的影响不容忽视;林春姣等[6]以桁式钢管混凝土拱桥为研究对象,考虑了遮挡的影响,采用数值模拟对拱肋各弦管的日照温度场进行了研究,结果表明下弦管受遮挡影响较大,导致上弦管较下弦管温度高;朱劲松等[7]提出一种三维遮光算法,可精确预测桥梁季节性温度场及应力效应,并得到夏季钢梁最大热应力达30 MPa,偏移最大为22 mm。不难看出温度荷载尤其是太阳辐射季节性变化对桥梁结构影响很大,但目前的研究仅局限于对钢管混凝土截面在日照温度荷载作用下的温度分布规律,以及截面温度应力定性及极值研究,缺乏对整个截面温度及应力效应的梯度分布计算模式研究,对减弱温度荷载病害的指导性不足。

基于温度场试验与有限元模拟相结合的方式,在已有研究的基础上,进一步探究钢管混凝土拱肋的日照温度场分布计算模式,及对最大温差下钢管和混凝土间的接触应力及接触间隙等效应的梯度分布进行分析,以期为防治因日照温度荷载造成的钢管混凝土拱肋脱空提供新思路。

1 日照温度场ANSYS模拟

1.1 日照辐射强度计算

结构温度场是温度在时间和空间上的一个三维瞬态分布,太阳辐射就是影响温度场分布的一个重要因素。目前,在结构工程领域最常用的太阳辐射计算模型是ASHRAE晴空模型[8]。任意构件表面上的总辐射强度Iθ包括:太阳直射辐射强度ID,θ、太阳散射辐射强度Id,θ和构件表面上获得的地面反射辐射强度IR, θ,计算如式(1):

Iθ=ID,θ+Id,θ+IR,θ

(1)

式中:Iθ的下标θ为所计算构件表面与地球水平面之间的夹角。

ID,θ、Id,θ、IR,θ计算如式(2)～式(4):

(2)

(3)

(4)

式中:IH为到达地球水平面上总的太阳辐射强度,IH=IDH+IdH;IDH为到达地球水平面的太阳直射辐射强度,IDH=I0PmIH;IdH为太阳散射辐射强度,IdH=1/2I0sinh(1-Pm)/(1-1.4lnp);I0为太阳常数,由I0=1 367[1+0.033cos(360N/365)]计算得到,N为日序数,P为大气透明系数,m为大气质量,忽略地球曲率影响可由m=1/sinh计算得到;h为太阳高度角,与赤纬角δ、时角ω以及观测点的地理纬度φ有关,δ=23.45sin[360×(284+N)/365],ω=15×(12-ST),ST为真太阳时,以24小时计,ST=北京时间-(120-当地经度)/15+td,td为时差,td=0.165sin2θN-0.025sinθN-0.126cosθN,θN为日序数变化的日角[9],θN=360(N-81)/364;太阳方位角α计算公式见文献[10];ρG为构件表面对太阳辐射的反射率,通常钢管表面取0.2;i为构件表面的太阳入射角,cosi=cosθ′sinh+sinθcoshcos(α-γ),θ′为任意表面倾斜角,γ为任意表面方位角。

以每个测点切线方向所在倾斜面上的太阳辐射强度来代替该测点的太阳辐射强度值,倾斜面太阳强度计算示意如图1,倾斜面上太阳光线角度参数示意图2。

图1 倾斜面太阳强度计算示意Fig. 1 Schematic diagram of solar intensity calculation on inclined plane

图2 倾斜面上太阳光线角度参数示意Fig. 2 Schematic diagram of angle parameters of sunlight on inclined plane

1.2 ANSYS热边界条件实现

计算钢管混凝土结构日照辐射温度场需要初始条件与边界条件2个重要的定解条件。初始条件取06:00左右截面的温度分布,并且假定此时截面温度分布均匀。边界条件包括钢管表面来自于太阳辐射的热流密度(第二类边界条件),与周围环境之间的对流和辐射热交换(第三类边界条件),钢管与混凝土之间的接触面热传递性能良好(第四类边界条件)[10]。第二类边界中的热流密度q(t)具体计算见式(5)～式(7),第三类边界条件由对流换热系数表征,其经验公式见(9),第四类边界条件在ANSYS中通过接触单元模拟。

q(t)=qs+qr

(5)

qs=0.6·Iθ

(6)

qr=εCs[εa(Ta(t)+273)4-(T+273)4]

(7)

Ta(t)=0.5(Tmax-Tmin)·sin[(t-t0)×15°]

(8)

(9)

式中:qs为太阳辐射钢管表面热流密度;qr为钢管表面长波辐射热流密度;ε为钢管表面辐射吸收率,金属材料表面可近似取0.9;Cs为蒂芬-玻尔兹曼常数,取5.67×10-8W/(m2·k4);εa为大气的长波辐射率,可近似取0.82;T为钢管混凝土拱肋表面温度;Ta(t)为外界大气温度,假定其按正弦函数变化;Tmax、Tmin分别为当日最高、最低气温;t0为当日最高气温出现的时刻;hc为对流换热系数;v为风速。

1.3 温度场有限元模型及其有效性

钢管混凝土的温度-应力场分析拟以四川省犍为岷江特大桥桥址处的一拱肋试验段为背景,选用规格为φ800 mm×10 mm×14 500 mm(直径×壁厚×长度)的钢管,内填C60自密实混凝土形成钢管混凝土构件,沿东-西方向水平放置于地面〔图3(a)〕。取距离构件左端7.0 m的截面,将截面等分为16份,并按照图3(b)的标记进行测点标号,使用红外线测温枪于2020年7月25日开始连续1个月采集钢管表面各测点温度值。

图3 钢管混凝土构件测点布置图及测温仪器Fig. 3 Layout of measuring points and temperature measuring instruments for concrete filled steel tubular members

由于钢管混凝土构件水平放置于地面上,截面能测量的有效测点只有1～13。

假设沿拱肋长度方向没有热传导,将温度场简化为平面二维温度场。采用ANSYS中热力耦合模型,定义钢管与混凝土为Plane55单元建立温度场分析模型,核心混凝土本构关系采用文献[11]的本构模型,在进行完温度热分析之后,将单元转换为Plane182,并将温度场分析结果作为边界条件进行结构分析。钢管与混凝土间采用面面接触单元模拟,钢管内表面采用TARGE169单元模拟,混凝土外表面采用CONTA172单元模拟,摩擦系数取0.6,设置法向接触刚度因子为0.1,刚度矩阵选择非对称阵。整个截面划分为1 561个节点和2 880个单元。温度-应力场分析中使用的材料热工及力学参数见表1。

表1 钢管、混凝土热工和力学参数表Table 1 Thermal and mechanical parameters of steel pipe and concrete

考虑到非线性温度场与时间的相关性,计算00:00到24:00的温度场,每小时划分为24个荷载步,时间子步为36 s,计算初始时刻设为06:00,初始温度取25 ℃。为检验有限元温度场分析结果的正确性,取钢管表面测点1、5、9绘制其实测与有限元模拟的温度时变曲线如图4。

图4 实测与有限元对比Fig. 4 Comparison between the measured and finite element model

从图4可知:实测值与模型计算变化曲线均先增大后减小,且出现最高温度的极值点处也相近,误差在2 ℃内,可认为拱肋日照温度场模型计算结果具有很好的准确性。拱肋在水平位置上东-西向放置,且钢管下部接近地面的测点,由于受到遮挡,其接受到的太阳辐射较少,因此其温度变化仅在25～35 ℃。在水平对称轴以上的测点,受到的太阳辐射多,且犍为县位于北回归线以北,正午时太阳在正南方向,因此,在14:00—15:00日照最强的时刻,钢管外的最高温度出现在接近钢管顶部偏南侧的测点9。

为进一步分析钢管混凝土截面温度场的空间分布规律,钢管混凝土拱肋截面在部分典型时刻下的温度场云图如图5。

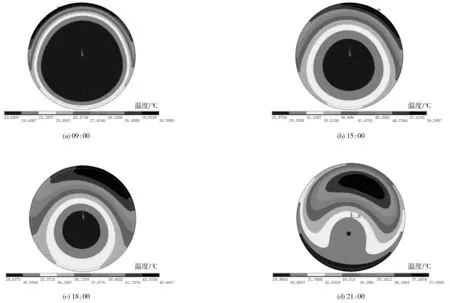
图5 典型时刻截面温度场云图Fig. 5 Nephogram of cross-section temperature field at typical time

由5图可知:

1)在日照辐射作用下,钢管混凝土拱肋截面温度场呈现出外高内低的不均匀分布状态, 15:00时钢管表面温度最高达到54.6 ℃,核心混凝土的圆心处只有25.9 ℃,最大梯度温差为28.6 ℃。这是因为钢管与混凝土作为2种材料,钢材导热系数约为混凝土的34倍,在相同时间内钢管能够迅速升温,混凝土则升温滞后。

2)09:00时钢管外表面最高温度仅有30.4 ℃,与大气温度接近; 15:00时钢管表面温度在太阳辐射作用下达到54.6 ℃,比当时气温(36.6 ℃)高出18.0 ℃;到18:00时随着太阳辐射强度的减弱,钢管表面温度开始下降,但随着热量由钢管表面向内部混凝土的传递,混凝土温度开始缓慢升高;到21:00,截面最高温度已移至核心混凝土,最高温度达到37.9 ℃,而此时大气温度29.8 ℃比核心混凝土低8.1 ℃。

3)太阳辐射对截面温度场分布的影响主要集中在与钢管壁临近的混凝土部分。在日照辐射的作用下,钢管升温较快,而与其接触的混凝土由于导热系数较小,温度传导较慢,因此温度场云图呈现出多层次温度分布,且沿半径方向梯度温差变化较大。

2 日照梯度温度模式分析

2.1 环向梯度温度分布模式

通过对日照温度场结果云图的观察,发现在接近钢管壁的混凝土存在着明显的温度梯度。因此,以测点所在位置夹角为θ坐标,温度值为ρ坐标,绘制典型时刻日照温度梯度玫瑰图如图6,以探析日照温度梯度的环向分布模式。

图6 典型时刻截面环向梯度温度玫瑰图Fig. 6 Temperature rosette of section circumferential gradient at typical time

由图6可知:

1)在不同的时刻,钢管外、内表面与核心混凝土外表面3者在环向上的温度分布曲线几乎重合。由于钢管是热的良导体,当钢管外表面接受到太阳辐射时,热量可在钢管厚度方向迅速传递至钢管内表面,同时钢管与混凝土间具有良好的热连续性,核心混凝土的外表面也几乎和钢管内表面温度一致。

2)09:00—15:00太阳辐射逐渐变强,截面的温度梯度也逐渐变大,最大温度梯度可达28 ℃,出现在钢管混凝土截面测点8、16连线,即与水平面成67.5°的方向上,这个方向正是太阳入射角30°的位置,此处太阳入射光线最接近垂直入射方向;混凝土温度梯度变化最快的范围是距离钢管表面100 mm以内的混凝土,超过100 mm后温度梯度变化不再明显,这与JTG D60—2015《公路桥涵设计通用规范》中推荐的表层混凝土梯度温度分布模式一致。

3)15:00过后,太阳辐射强度逐渐减弱,钢管导热系数较大,降温快。接近钢管的混凝土温度会由于外部热量的传导而逐渐升高,到18:00时钢管混凝土最大梯度温差仅5 ℃左右,之后钢管混凝土内部梯度温度场并没有显著变化。

2.2 径向梯度温度分布模式

桥梁结构的温度梯度分布模式已有大量研究,但主要是针对钢箱梁或混凝土箱梁的梯度温度分布模式,计算曲线多为多段折线、抛物线以及指数函数[12-14]。而对于钢管混凝土这一组合结构,其截面梯度温度分布计算模式还有待研究。

梯度温度为结构断面各点温度与该断面上最低温度的差值[15]。通过钢管混凝土构件截面环向梯度温度玫瑰图可以看出,在径向的67.5°方向上温度梯度变化最大,因此提取15:00时沿径向67.5°方向的温度值,分析钢管混凝土径向梯度温度场的分布模式,并以15:00时该径向最低温度为温度基准值,计算径向不同深度处的梯度温度(图7),同时以钢管直径D为基准值进行无量纲化,用y/D来表征各点在径向的位置关系,作为对比图7还给出了JTG D60—2015《公路桥涵设计通用规范》、TB 10092—2017《铁路桥涵混凝土结构设计规范》中的梯度温度分布模式。

图7 15:00径向梯度温度分布曲线比较Fig. 7 Comparison of radial gradient temperature distribution curves at 15:00

由图7可以看出:

1)在距离钢管表面10 cm范围内,钢管混凝土沿径向的温度变化梯度的计算结果明显高于2本规范,相同位置处钢管混凝土温度比JTG D60—2015中推荐值高5 ℃左右,比TB 10092—2017中推荐值大8 ℃左右。

2)在距离钢管表面10～20 cm范围,2本规范推荐的温度变化梯度均比数值模拟结果小,且数值模拟结果逐渐接近于TB 10092—2017温度梯度曲线。

3)钢管混凝土梯度温度场的分布深度大约为40 cm,这点与JTG D60—2015中推荐值一致,仅为TB 10092—2017推荐值的50%。数值计算结果表明,钢管内部的梯度温度场并不符合规范中推荐的单调分布规律,在距离钢管表面40 cm(D/2)后钢管混凝土内的温度随径向深度增加而增大。

鉴于在钢管混凝土梯度温度场的分布深度40 cm范围内其沿径向的分布整体呈现指数分布的规律,参考TB 10092—2017使用式(10)描述径向梯度温度的计算模式:

Ty=T0e-αy

(10)

式中:T0指截面径向最大的温度梯度值,取30 ℃;y为计算点与构件上表面的径向距离;Ty为计算点位置处的温度梯度值;α为指数值,由数值计算结果拟合确定。表2为在径向梯度温度变化较大的40 cm范围内截面径向梯度温度计算模式的特征参数取值,其拟合曲线与数值模拟计算结果能够较好的吻合。

表2 钢管混凝土截面径向梯度温度计算模式的特征参数取值Table 2 Characteristic parameter values for radial gradient temperature calculation mode of steel tube concrete cross-section

对于截面径向在水平对称轴以下的部分(距钢管表面距离>40 cm),其梯度温度随距钢管上表面距离的增大而增大,此时仍采用以e为底的指数分布来计算并不合理,因此根据数值模拟计算结果曲线趋势,采用幂函数能更好地描述距钢管表面40 cm以外部分的梯度温度计算模式,其计算形式可假设为:

Ty=T1yα

(11)

式中:T1为距离钢管拱顶表面最远的径向拱底温度值,取35 ℃;由数值结果拟合取α=6.5。截面径向水平对称轴以下部分的梯度温度计算模式为:

Ty=35y6.5

(12)

2.3 最大梯度温差的时变规律

为说明钢管混凝土截面中最大温度梯度随时间的变化规律,图8给出了截面沿67.5°方向上钢管外表面与距离钢管表面5、10、20、40 cm深度处的最大梯度温差随时间的变化规律。

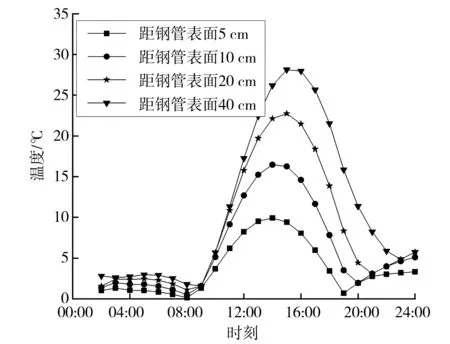
图8 67.5°方向上不同深度处截面最大梯度温差的时变规律 Fig. 8 Time-varying law of the maximum gradient temperature difference at different depths of the cross-section in the 67.5 ° direction

由图8可知: 10:00时不同深度处的梯度温差均出现快速上升,下午14:00—15:00时左右梯度温差达到峰值,钢管表面与40 cm深度处温度差最大值达到28 ℃,之后随时间逐渐降低;距离钢管表面的深度越大,最大梯度温差越大但达到峰值的时间越晚,梯度温差降低的速率也越慢,这是由于作为热不良导体的管内混凝土热量向径深的传导本就困难,需要长时间辐射热量的输入,这也导致了深度越深的混凝土温度升高越慢,达到峰值温度需要的时间越长,太阳落山后钢管外侧温度下降很快,而管内核心混凝土中积累的热量不容易向外扩散,温度下降所需时间也最长。

3 钢管-混凝土截面接触应力分布

钢管和内部混凝土的密切粘结是钢管混凝土结构套箍效应发挥的前提。由于钢管和混凝土热传导性能的显著差异,日照辐射下钢管混凝土内部存在较大的温度梯度,这种梯度温差将导致钢管和混凝土的界面产生拉应力[16]。

3.1 梯度温度应力空间分布模式

图9给出了15:00时接触单元的接触应力和接触间隙的云图及典型时刻环向分布,图9中CONTPRES指接触面之间的压力,正值是压应力,负值是拉应力;CONTGAP指的是接触面之间的分离距离,通常是负值,没有分离则为0。

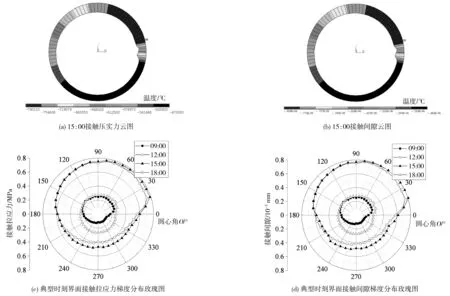
图9 典型时刻钢管和混凝土界面接触拉应力与接触间隙梯度分布云图及空间分布玫瑰图Fig. 9 Gradient distribution nephogram and spatial distribution rosette of contact tensile stress and contact gap between steel tube and concrete at typical time

由图9可知,日照辐射梯度温度导致钢管管壁与内部混凝土之间存在拉应力,具体而言:

1)钢管-混凝土界面接触应力沿周向呈现不均匀分布特征,向阳侧明显大于背阳侧;在梯度温差最大的15:00时,钢管-混凝土界面的接触拉应力最大达0.79 MPa,出现在拱顶偏南的位置,最小为0.47 MPa,出现在拱底与地面接触的位置;钢管-混凝土界面的接触拉应力随时间的增长呈现出先增大后减小的规律,并且在最高温度处拉应力增长速度最快(增长值也最大),整个截面最大梯度应力出现在梯度温差最大处,即与水平面成67.5°的拱顶位置。

2)接触间隙的分布规律与接触拉应力规律一致,即钢管-混凝土界面的接触间隙随着2者间的接触拉应力的增大而增大;最大接触间隙达0.809×10-3mm,出现在最大接触拉应力处,最小接触间隙达0.482×10-3mm,出现在最小接触拉应力处。

3)从图9(c)中可以看出,09:00—12:00时温度升高较大,钢管-混凝土界面接触应力增幅较大,最大应力出现的位置由150°方向的位置变化到67.5°的位置;而15:00—18:00时日照温度逐渐减弱,界面接触应力明显减小。

3.2 梯度温度应力时变规律

为说明钢管-混凝土界面接触应力随时间的变化规律,给出了全截面最大梯度温度应力随时间的变化曲线如图10。

图10 最大梯度温度应力时变曲线Fig. 10 Time-varying curve of the maximum gradient temperature stress

由图10可知:从00:00—07:00,界面接触应力为压应力,量值在0.1 MPa左右;从08:00—20:00,界面接触应力表现为拉应力,且随时间呈现先增大后减小的变化趋势,最大拉应力接近0.8 MPa,出现在14:00、15:00,在20:00时后界面接触拉应力又变为压应力。可见在四川地区夏季日照辐射下,钢管-混凝土界面接触应力在1 d的时间内会出现接近1.0 MPa的周期性变化,且0.8 MPa的拉应力达到平均粘结强度(0.4 MPa左右)的2.0倍,因此,设计和施工过程中应该关注日照梯度温度荷载导致的钢管-混凝土界面接触应力,采用适当方法使管内混凝土产生超过0.8 MPa的膨胀压应力,避免管内混凝土出现脱空现象[17]。

4 结 论

通过钢管混凝土拱肋截面日照温度场试验与有限元模型,针对整个截面梯度温度及接触应力、间隙等效应结果,建立梯度分布模式,进行深入分析,主要结论如下:

1)管内混凝土梯度温差在1 d时间内呈现先增大后减小的变化规律,10:00时不同深度处的梯度温差均开始快速上升,下午14:00、15:00时左右梯度温差达到峰值随后随时间逐渐降低。

2)钢管混凝土径向梯度温度计算模式采用分段函数。在沿径向40 cm深度范围内采用指数分布,并且距钢管外表面深度D每增加10 cm,特征参数增大约1;在40 cm以外,采用幂函数分布。

3)钢管-混凝土界面的梯度温度应力空间分布模式呈现出沿周向分布不均匀的特征,并且向阳侧明显大于背阳侧;在时间上呈现极大的周期性,00:00—08:00界面表现为最大0.2 MPa的压应力,08:00—20:00界面为拉应力,并在14:00、15:00达到最大0.8 MPa,超出钢管管壁与混凝土之间的平均粘结强度近一倍。