基于EEMD-LSTM的桥梁变形响应组合预测模型研究

2023-07-14孟庆成李明健吴浩杰

重庆交通大学学报(自然科学版) 2023年5期

孟庆成,李明健,胡垒,万达,吴浩杰,齐欣

(1. 西南石油大学土木工程与测绘学院,四川成都 610500; 2. 西南交通大学土木工程学院,四川成都 610031)

0 引言

截止2020年年底,我国已建成公路桥梁总长6 628.55万m,共计91.28万座。数量众多的桥梁受到各种情况及降雨、降雪和温差等环境因素的综合影响,会出现变形现象。桥梁变形超过一定限值将会对桥梁结构造成损伤,并导致承载力降低等病害出现。因此,为保障桥梁运营安全性和耐久性,建立高精度的桥梁变形预测模型十分有必要[1],这对桥梁结构安全状态预警有着重大意义。

近年来,随着人工智能发展,运用智能化手段开展桥梁结构状态和安全评估成为桥梁健康监测的发展趋势[2]。国内外学者展开了大量研究,陈国良等[3]通过搭建差分整合移动平均自回归模型(ARIMA)来预测桥梁挠度,并以黄冈长江大桥进行了实例验证;郑栋等[4]采用基于Bayesian理论的融合方法,根据历史监测数据对路堤沉降进行了预测;WANG Xudong等[5]基于融合思维进化算法(MEC)和反向传播算法(BP),建立了优化神经网络模型,并通过CSWs-PC桥的实例,验证了该模型比传统BP神经网络更优的预测性能;吴杰等[6]利用小波神经网络(WNN)预测了桥梁横向位移,仅用少量的监测数据训练就取得了较好的预测结果;栾元重等[7]基于RBF神经网络模型预测了桥梁变形,获得了较高的短期预测精度;WANG Hao等[8]采用改进后的Bayesian模型,准确预测了由温度引起的桥梁结构响应;田壮等[9]建立了斜拉桥有限元模型,并以有限元模拟结果为训练数据,搭建了BP神经网络模型预测结构变形响应,准确率均超过90%。然而上述预测模型均属于静态模型,忽略了结构变形动态本质,模型在训练时没有连接到不同时刻的变形状态,限制了预测精度的进一步提升[10]。

当前用于时间序列数据的动态预测模型主要是基于循环神经网络(RNN)建立的[11],长短期记忆神经网络(LSTM)作为一种特殊的RNN,可有效解决传统RNN在处理实际问题中因数据时效性等不足的缺陷。LSTM具备强大的非线性处理、学习和记忆能力,在处理长时间序列数据预测中具有显著优势,可广泛运用于各种时序数据预测[12]。桥梁结构变形具有复杂性和多尺度性,采用单一模型预测难以充分挖掘桥梁变形响应在不同尺度分量的特征,存在较多局限,而采用组合模型能实现不同方法的信息整合,可提高模型精度、稳定性和适用性。因此笔者提出了一种结合集合经验模态分解 (EEMD)和长短期记忆神经网络的(LSTM)方法,通过建立EEMD-LSTM桥梁变形组合预测模型,以武汉沌口长江大桥为实例进行分析,验证该方法的有效性。

1 桥梁变形预测模型

1.1 集合经验模态分解法(EEMD)

经验模态分解法(EMD)可将任意时间序列信号中的不同尺度分量依次分解,产生多组尺度特征互异的数据序列,每组数据序列都是一个本征模态函数(IMF)[13]。

集合经验模态分解法(EEMD)是EMD的改进方法。首先对输入信号中加入白噪声,再进行EMD分解,将多次分解后IMF分量对应求均值[14],并给定一个原始输入信号x(t),EEMD处理过程如图1。

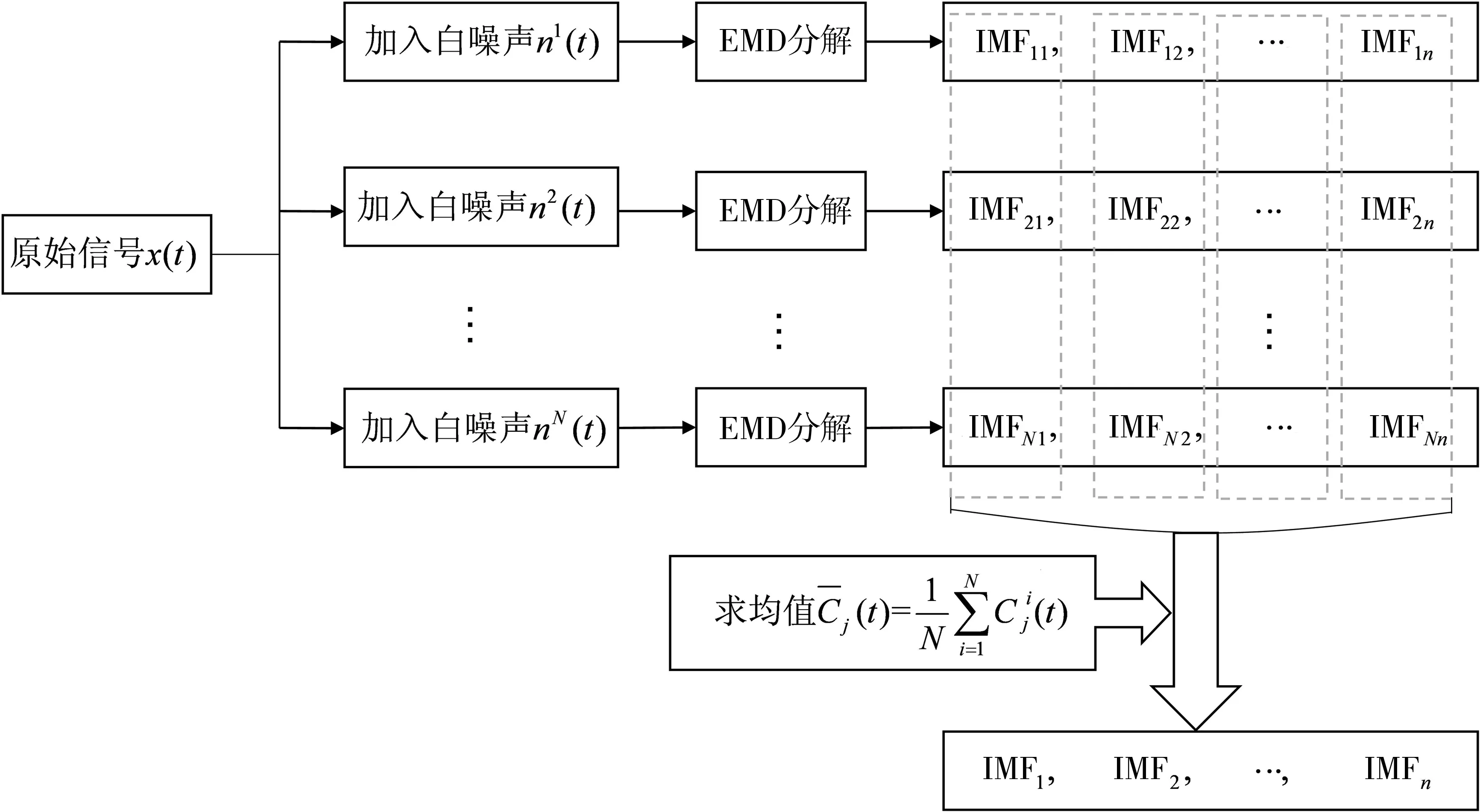
图1 EEMD分解时间序列信号流程Fig. 1 EEMD decomposition time series signal flow chart

EEMD在分解时间序列信号时添加了白噪声,可消除EMD分解时的模态混叠问题,且保证了最终分解结果在物理上的唯一性。加入时间序列信号的白噪声均匀分布且均值为0,多次平均处理后会相互抵消,不会对真实时间序列信号结果造成影响。其分解过程如下:

1)原始时间序列信号x(t)加入符合正态分布的高斯白噪声ni(t),形成新的时间序列信号xi(t),其计算如式(1):

xi(t)=x(t)+ni(t)

(1)

式中:i为增加的白噪声次数。

(2)

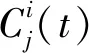
3)重复以上两个步骤N次,并将各对应的IMF分量相加再求均值,如式(3):

(3)

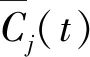
4)最终原始时间序列信号x(t)经过EEMD分解后可表示为:

(4)

1.2 长短期记忆神经网络(LSTM)

循环神经网络(RNN)与传统的人工神经网络(ANN)隐藏层节点间的连接结构不同。人工神经网络(ANN)隐藏层间的节点相互独立,循环神经网络(RNN)在隐藏层的邻近节点间相互连接,RNN和ANN结构对比如图2。RNN隐藏层节点不仅要接收输入节点信息,还要接收上一个隐藏节点的输入信息,由于其特殊的网络结构,RNN可对历史信息进行存储,具备记忆功能,可将存储的历史信息用于输出计算,因此RNN在预测时间序列数据时具备很大优势[15]。

图2 RNN和ANN结构对比Fig. 2 Structure diagram comparison of RNN and ANN

RNN在实际处理长时间序列问题时,存在数据时效性等局限性,长短期记忆神经网络(LSTM)可很好弥补RNN在处理长序列问题的不足[16]。LSTM可将遗忘门、输入门、输出门和记忆单元组成特定结构来替代RNN中的隐藏层神经元,这个结构可让LSTM有选择性地筛选状态信息、控制信息传递,极大提升了处理长时间序列问题的性能。LSTM基本单元结构如图3。

图3 LSTM基本单元结构示意Fig. 3 Structure diagram of LSTM basic unit

笔者以第2个基本单元为例,xt为t时刻网络的输入;ht为t时刻网络的输出;ct-1为t-1时刻单元的状态;ct为t时刻单元的状态;tanh为双曲正切函数,可将数值映射到[-1, 1];σ为Sigmoid激活函数,可将数值映射到[0, 1],其中0表示历史信息全部丢弃,1表示历史信息全部保留。LSTM模型关键在于基本单元间状态的传递,通过3个门的组合来控制信息输入及输出,决定单元状态[17]。3个门限结构具体计算过程为

ft=σ(Wfxxt+Wfhht-1+bf)

(5)

it=σ(Wixxt+Wihht-1+bi)

(6)

Ot=σ(WOxxt+WOhht-1+bO)

(7)

式中:ft、it、Ot分别为遗忘门、输入门、输出门在t时刻的输出结果向量;Wfx、Wix、WOx分别为遗忘门、输入门、输出门的输入和隐藏节点权值矩阵;Wfh、Wih、WOh分别为遗忘门、输入门、输出门的隐藏和输出节点的权值矩阵;bf、bi、bO分别为遗忘门、输入门、输出门的偏置向量。

1.3 EEMD-LSTM模型

桥梁在运营过程中受汽车荷载、风荷载及温度等因素综合作用,不同的作用时间、作用周期和影响因素存在差异,因此桥梁结构变形响应存在多尺度效应。针对桥梁变形响应特性,笔者将EEMD分解算法和LSTM网络融合,提出了一种EEMD-LSTM的桥梁变形组合预测模型。从布置于桥梁结构上的多个监测传感器获取环境信息和变形数据,对数据信息进行整理和预处理,使其满足模型的数据格式要求并剔除异常数据。EEMD算法将变形时间序列依次分解成不同尺度特征的IMF分量和一个剩余分量Res,再搭建LSTM模型提取各变形分量特征并预测其发展趋势,然后重构各分量预测值并叠加求和,所得结果即为模型预测变形值,最后对模型预测精度进行评价。EEMD-LSTM预测技术路线如图4。

图4 EEMD-LSTM模型技术路线Fig. 4 EEMD-LSTM model technology roadmap

2 预测效果评价指标

均方根误差RMSE(ERMS)、平均绝对误差MAE(EMA)、平均绝对百分误差MAPE(EMAP)和决定系数(R2)是评价时间序列数据预测效果的重要指标。ERMS表征预测值偏离实测值程度;EMA表征预测误差实际情况;EMAP表征绝对百分比误差平均大小;R2表征模型拟合精度。其中:R2越接近1,ERMS、EMA和EMAP越小,模型预测精度越高。各评价指标计算为:

(8)

(9)

(10)

(11)

3 工程实例

3.1 工程概况

武汉沌口长江大桥是长江首座按照双向八车道设计的特大公路桥。该桥于2014年12月动工建设,2017年12月正式运营,桥梁全长8.599 km,桥面全宽46 m,设计速度为100 km/h;主桥为双塔双索面斜拉桥,采用PK断面钢箱梁,主塔高233.7 m,采用钻石型结构,斜拉索选用204根平行钢丝斜拉索,极限强度为1 760 MPa,呈扇形布置;主桥为半漂浮结构体系,全长1.51 km,最高通航水位和最低同行水位分别为26.81、10.17 m;根据桥址地形地质条件、通航要求、结构合理以及经济等要求,选用(100 + 275 + 760 + 275 + 100)m的跨径组合[18]。桥梁立面布置如图5。

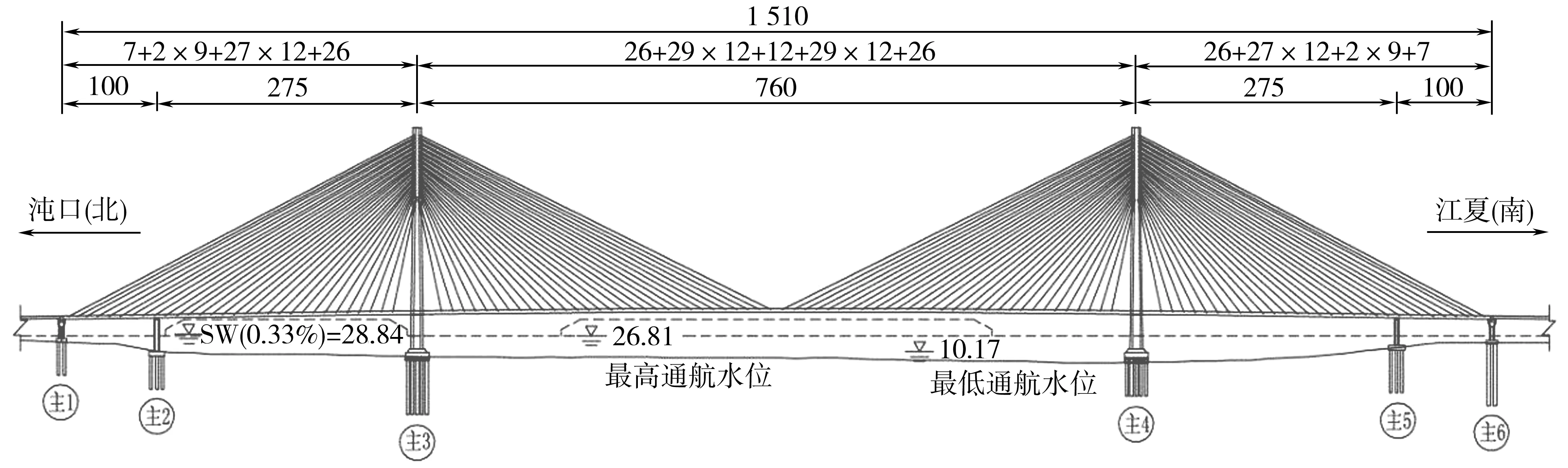
图5 武汉沌口长江大桥立面布置(单位:m)Fig. 5 Elevation of Wuhan Zhuankou Yangze River Bridge

3.2 数据集获取及预处理

该桥建成运营后的健康监测内容包括主梁挠度、温度、斜拉索索力、风向风速、倾角、主塔应变和桥梁动力特性等。笔者选取2021年5月1日—2021年5月31日的桥梁跨中挠度和环境监测数据作为数据集,监测周期为1 h,共744组数据。每组数据包括桥塔塔顶和桥梁跨中截面处的温度、湿度、风向、风速及桥梁跨中位置挠度变形数据,部分监测数据如表1。

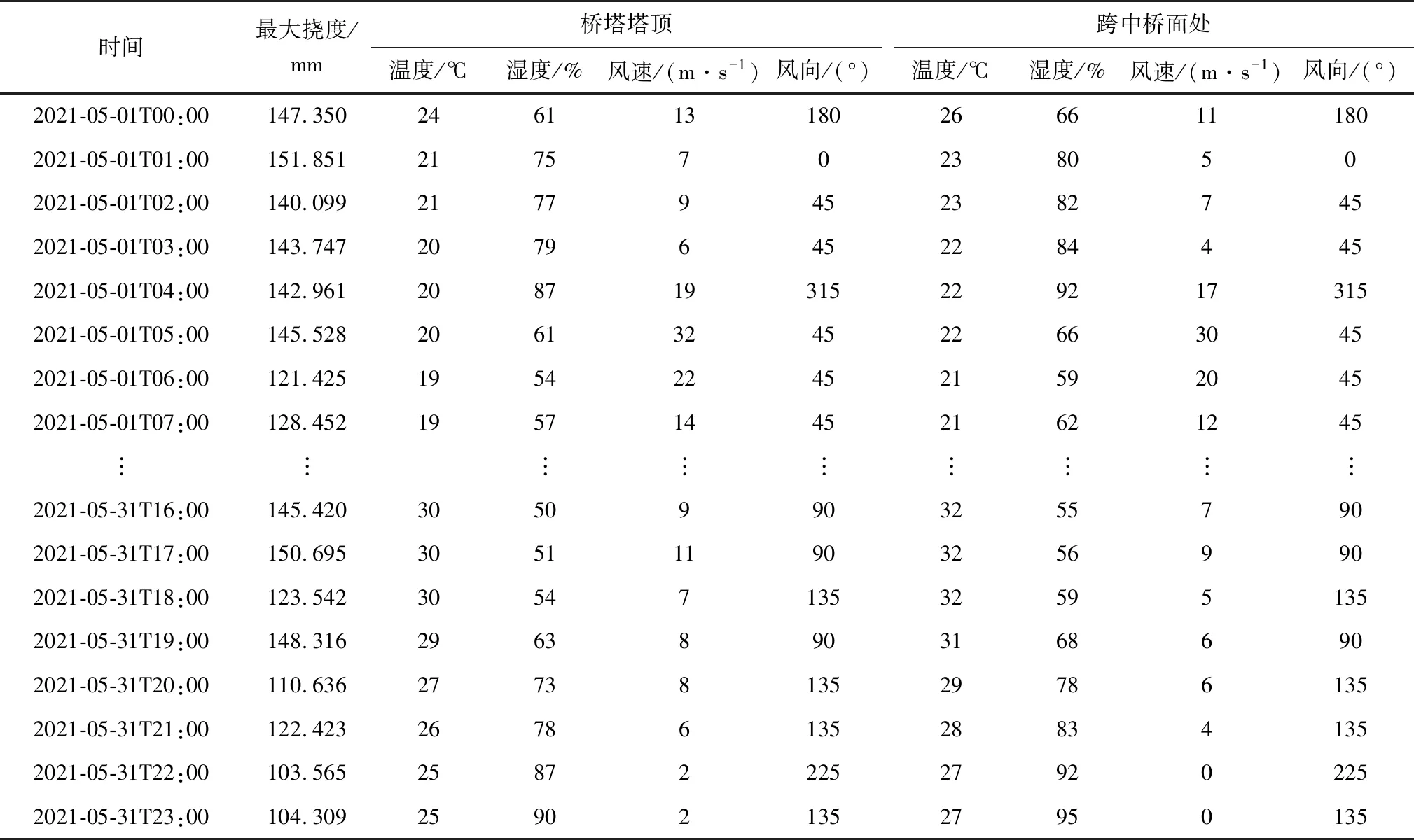
表1 武汉沌口长江大桥变形监测数据Table 1 Deformation monitoring data of Wuhan Zhuankou Yangze River Bridge

对获取数据进行如下预处理:

1)归一化处理:桥梁变形数据和环境参数量纲和大小有较大差异,原始数据直接用于模型训练会影响模型的计算效率,故需要对数据进行归一化处理,将数据范围映射到[0, 1],再输入网络模型训练时可加快其收敛速度,其计算如式(12):

(12)

式中:x为原始变形数据;xmin、xmax分别为变形数据最小值、最大值;x′为归一化计算后的结果。

在归一化处理过程中,异常值不会对归一化结果造成影响,但为避免对预测精度造成影响,在后续工作中会对其识别并剔除。

2)孤立森林算法(iForest)降噪:该算法适用于时间序列数据的异常检测,基本思想是把异常数据归结为“少量和不同”,即异常数据只占全部数据的少许比例,且异常数据特征与前后正常数据特征有较大差异。iForest算法原理是用随机特征的超平面对数据进行切割成两个子数据空间,再分别对各子数据空间进行切割,循环进行上述步骤直到每个数据空间仅包含单个数据时停止切割,由此形成孤立树,根据仅包含一个数据叶子结点x到根节点路径长度h(x)来计算异常分值,进而判断数据是否存在异常。其计算如式(13)～式(15)。

(13)

c(n)=2H(n-1)-[2(n-1)/n]

(14)

H(i)=lni+0.577

(15)

式中:s(x,n)为异常分值,s(x,n)越接近1说明存在异常数据可能性越高,若测试数据在0.5左右,则说明全部数据没有明显异常值;E[h(x)]为待检测数据x在孤立森林中的平均路径长度;c(n)用于对路径长度h(x)的标准化。

在桥梁变形监测中,难免会出现通讯信号干扰、传感器数据漂移等情况,这会导致监测数据存在异常值。为消除异常数据干扰,笔者引用孤立森林算法进行检测并处理变形异常数据;变形时间序列共检测出19组异常值(图6),对异常数据进行剔除。

图6 变形时间序列异常点检测结果Fig. 6 Abnormal point detection results of deformation time series

3)数据集划分:原始变形时序数据剔除掉19组异常值后还剩余725组,选取前675组数据作为训练集,后50组数据作为测试集。训练集用于参与模型参数和权重更新;测试集用于评价模型预测精度高低,判断模型的泛化能力。

3.3 桥梁变形分量预测

3.3.1 EEMD分解变形时间序列

桥梁结构变形响应存在多尺度效应,为充分挖掘不同时间尺度的变形响应特征,获得其演变趋势规律,笔者采用EEMD对桥梁变形时间序列进行多尺度分解,为提升模型泛化能力,向剔除异常数据后的桥梁变形时间序列加入均匀分布白噪声。变形时间序列经EEMD自适应分解成9个IMF分量和1个剩余分量Res,如图7。

图7 EEMD分解变形时间序列结果Fig. 7 EEMD decomposition results of deformation time series

3.3.2 EEMD-LSTM模型分量预测

超参数和优化器等对搭建的EEMD-LSTM模型预测结果有重大影响。为获取最优的预测精度,笔者设计了不同的超参数(神经元、批大小等)、回望窗口和优化器进行组合。经模型验证,当神经元为20个、批量大小为24、回望窗口为6及Adam优化器的组合为最优参数组合,此时EEMD-LSTM模型对不同尺度IMF分量和剩余分量Res的预测结果如图8。对IMF分量和Res预测结果进行线性求和,再进行反归一化处理即为桥梁变形的最终预测结果。

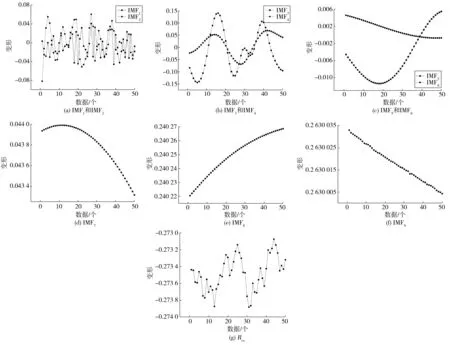
图8 IMF分量和剩余分量Res预测结果Fig. 8 Prediction results of IMF and Res

3.4 不同模型结果对比分析

为综合比选各类算法变形预测效果,将EEMD-LSTM组合预测模型和单一Bayesian模型[19]、支持向量机SVM模型[20]、LSTM模型进行对比分析。其中:Bayesian模型误差精度为5×10-4,超参数α1=α2=λ1=λ2=1×10-6;SVM模型核函数选linear,正则化系数c=1;LSTM模型采用和EEMD-LSTM模型相同的超参数组合。各模型变形预测结果对比如图9。图9中:Bayesian模型、SVM模型和LSTM模型都能较为准确地预测桥梁变形趋势,但在变形发生突变时,这3种模型预测值和实测值存在一定误差。相比于上述这3种模型,EEMD-LSTM模型不仅能很好地预测桥梁变形趋势,且预测值和实测值数据非常契合,预测误差更小,在预测过程中运行速度更迅速,鲁棒性更好。

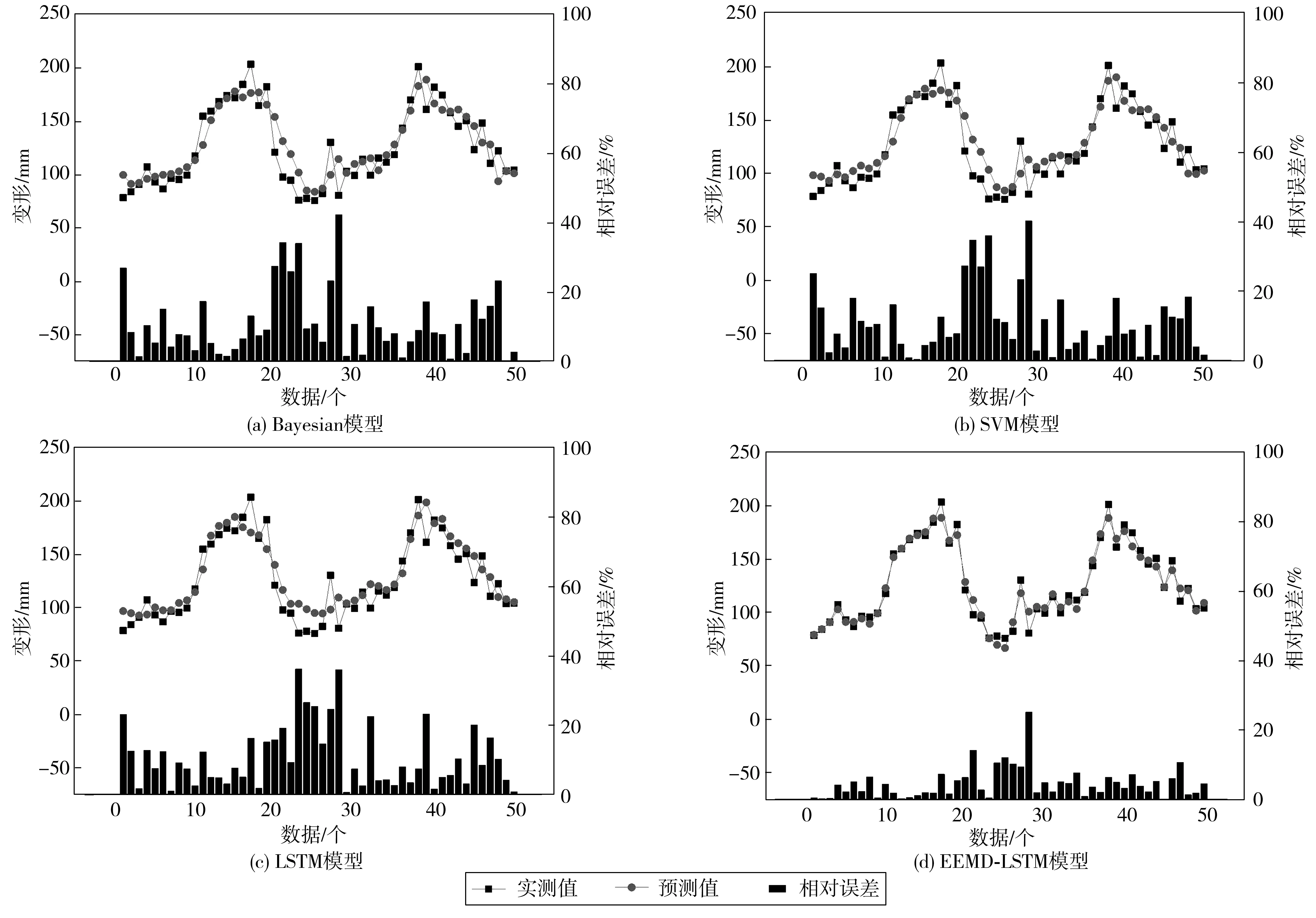
图9 不同模型变形预测对比Fig. 9 Comparison of deformation prediction of different models

在相同实验条件下,选取ERMS、EMA、EMAP和R2对各模型预测结果进行定量对比,如表2。由表2可知:LSTM模型变形预测精度高于SVM和Bayesian模型。对SVM和Bayesian模型而言,在模型训练时只能学习当前时刻信息,无法连接不同时刻的变形状态,从而导致长期历史信息会影响模型预测精度,限制了模型预测精度的进一步提升; LSTM模型训练时能有选择性地筛选状态信息,对变形的历史信息进行存储并加以利用,在变形预测时能获取前后关联信息,能更好地处理时间序列数据。

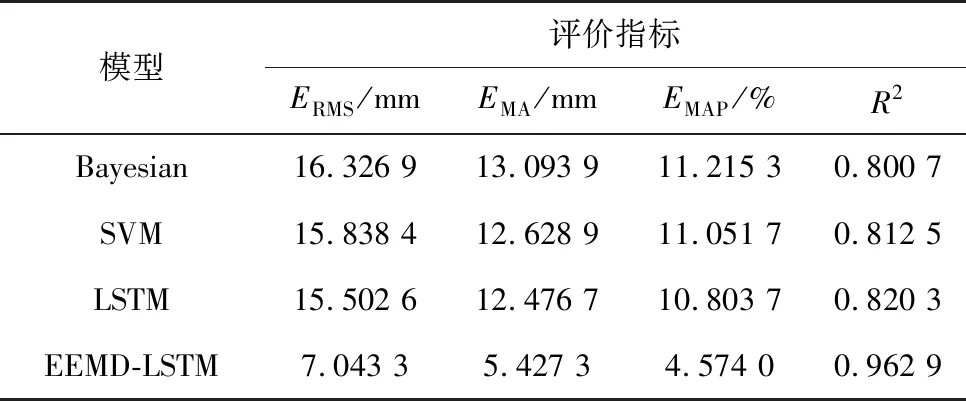
表2 不同模型评价指标结果对比Table 2 Comparison of evaluation results of different models

EEMD-LSTM模型与Bayesian模型相比:ERMS、EMA和EMAP分别降低了56.86%、58.55%和59.22%,R2提升了20.14%;与SVM模型相比:ERMS、EMA和EMAP分别降低了55.53%、57.02%和58.61%,R2提升了18.51%;与LSTM模型相比:ERMS、EMA和EMAP分别降低了54.57%、56.50%和57.66%,R2提升了17.38%。EEMD-LSTM模型较其他3种模型在预测精度上有很大提升,这是因为桥梁变形具有多尺度特征,不同尺度变形分量波动特征不同,采用单一预测模型存在一定局限性,难以识别其差异性,这就造成预测精度难以进一步提升。采用EEMD-LSTM模型会先对桥梁变形序列在不同时间尺度上进行分解,再在不同时间尺度变形分量上提取变形特征,契合了桥梁变形的多尺度特性。与单一模型相比,EEMD-LSTM模型充分发挥了EEMD分解法和LSTM模型在处理时序数据上的优势,在面对新的变形序列时可获得更加稳定和精确的预测结果,提升了模型鲁棒性和适用性。