基于Winkler地基叠合梁的不均匀沉降作用下的无砟轨道变形研究

颜建伟,熊 明,谭 鑫

(1. 华东交通大学 江西省地下空间技术开发工程研究中心,江西 南昌 330013;2. 华东交通大学 土木建筑学院,江西 南昌 330013)

0 引 言

无砟轨道因耐久性好、维修少和稳定性高等特点成为了高速铁路轨道广泛采用的主要结构形式[1]。轨道下土质路基承载能力相对较弱,且受重力、列车动荷载和地下水等各种环境因素的长期循环作用,易发生不均匀累积变形形成局部沉降[2]。双块式高速铁路无砟轨道道床结构和支承结构都是现浇成的混凝土结构层,其整体性较强,在轨下路基局部沉降作用下易发生较大的结构变形,导致轨面不平顺,影响轨道的服役性能[3]和列车的安全平稳运行。

众多学者已开展了大量轨下路基沉降影响上部轨道受力与变形的研究,通常采用叠合梁、梁-板、梁-体等分析模型[4]。肖威等[5]基于轨道路基梁-体有限元模型探究了CRTS Ⅲ 型板式无砟轨道在不同沉降条件下的附加变形;XU Qingyuan等[6]建立了板式无砟轨道的三维非线性梁-体有限元模型,研究了路基不均匀沉降作用下轨道的空间力学特性;JIANG Hongguang等[7]通过轨道路基三维有限元模型,模拟不同沉降条件下无砟轨道结构的变形和附加应力,揭示了路基沉降下路基表面到轨面的传递特性;CUI Xuhao等[8]建立考虑路基不均匀沉降的轨道三维有限元模型,分析了路基沉降对CRTS Ⅱ 板式无砟轨道结构层界面力学性能和损伤行为的影响;赵立宁等[9]取单元板式无砟轨道为研究对象,建立路基-轨道有限元模型,探讨了地面沉降和轨道结构层间离缝对轨道面平顺性的影响;蔡小培等[10]研究了地面不均匀沉降时,沉降范围和形式对双块式无砟轨道变形的影响规律;向俊等[11]建立CRTS Ⅰ 和CRTS Ⅱ 型2种轨道的梁-体有限元模型,分析了路基不均匀沉降对这2种轨道结构变形、层间离缝的演化和轨面局部上拱的影响。

有限元等数值模拟技术[12]的发展,快速推进了路基不均匀沉降下轨道的变形研究[13],驱动形成的规律性研究极大促进了高速铁路的发展。笔者针对双块式无砟轨道结构,建立Winkler地基叠合梁解析模型,来研究路基不均匀沉降下波长和幅值耦合作用上部轨面的变形规律,旨在与数值模拟技术相辅相成,为高速铁路路基沉降和轨面不平顺控制提供快速理论分析方法。

1 双块式无砟轨道模型

1.1 Winkler地基叠合梁模型

双块式无砟轨道结构主要包括钢轨、弹性扣件、轨枕、道床板、支承层等,其断面几何尺寸如图1。

图1中E1I1、E2I2分别为道床板与支承层的抗弯刚度。相对于轨道纵线,路基的横断面尺寸小得多,路基横向范围内的沉降可按照均匀变形处理,仅考虑其沿轨道纵向沉降变形的作用。基于Winkler弹性地基叠合梁模型,将钢轨考虑为简支梁,扣件视作等间距点支撑的线弹簧,支承层和道床板视为紧密联接的双层叠合梁,即一整体梁,其等效物理中平面的形心坐标可表示为:

y0=(A1y1n+A2y2)/(A1n+A2)

(1)

式中:y1和y2分别为道床板和支承层的横向形心坐标;A1和A2分别为道床板和支承层的横断面面积;n为道床板与支承层弹性模量比值E1/E2。

叠合梁整体梁的等效抗弯刚度为:

(2)

式中:E0、I0分别为等效叠合梁的弹性模量、截面惯性矩,a1、a2为道床板、支承层形心到等效物理中平面形心距离;h1、h2为道床板、支承层厚度。

高速铁路土质路基大多属于弹性地基,符合Winkler弹性地基的假定。对路基不均匀沉降的模拟,国内外的选择略有不同,有折角型、错台型、正弦型、指数型和余弦型。笔者的路基不均匀沉降采用国内常用的下凹全波余弦曲线来模拟[14],如图2。

图2 下凹全波余弦型不均匀沉降曲线路基模型Fig. 2 Uneven settlement subgrade model with full concave wave cosine curve

轨下路基表面不均匀沉降数学描述为:

(3)

式中:A为不均匀沉降幅值;s为波长;x为任意沉降点到沉降中心的距离。

双块式无砟轨道叠合梁模型如图3。

图3 双块式无砟轨道叠合梁模型Fig. 3 Composite beam model of double-block ballastless track

由Winkler弹性地基上梁挠曲微分方程可得:

(4)

式中:w(x)为叠合梁挠度;k为地基反力系数;Pi为作用于叠合梁上的第i个扣件力;δ(·)为脉冲函数。

微分方程求解分2个步骤进行,首先考虑地基反力,结合图3的双块式无砟轨道叠合梁模型,根据对称性考虑右侧叠合梁的变形,式(4)可改写为:

(5)

式中:w1(x)为沉降区叠合梁挠度;w2(x)为非沉降区叠合梁挠度。

当0≤x≤s/2时,式(5)通解为:

w1(x)=eβx(C1cosβx+C2sinβx)+e-βx×(C3cosβx+C4sinβx)+B1cosαx+B2

(6)

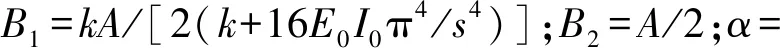
根据对称性,边界条件有:

(7)

代入(6)式可得,C1=C3,C2=-C4,则式(6)可改写为:

w1(x)=2C1coshβxcosβx+2C2×sinhβxsinβx+B1cosαx+B2

(8)

当x>s/2时,无穷远处叠合梁挠度为0,有:

w2(x)=e-βx(D1cosβx+D2sinβx)

(9)

式中:D1、D2均为待定系数。

综合可得路基不均匀沉降下Winkler弹性路基梁的挠度为:

(10)

根据变形连续条件,有:

(11)

可确定出系数C1、C2、D1、D2。

考虑各节点扣件力作用时,叠合梁总变形为:

wbi=wi+wpi,i=1～N

(12)

式中:wpi表示叠合梁受第i个扣件作用发生的挠曲变形,且有:

(13)

式中:fij为叠合梁在第i个扣件节点处由作用于第j个扣件节点处的单位力而引起的竖向变形;Pj为第j个扣件力;N为扣件总数。由Winkler地基上无限长梁受集中力作用的弯曲变形公式,可得:

(14)

式中:|xi-xj|为扣件节点i和j的间距。

扣件力作用下钢轨变形为

(15)

式中:wri为钢轨第i个扣件节点处的挠度;dij为钢轨第i个扣件节点处受第j个扣件节点单位力引发的变形。基于钢轨简支梁模型,有:

(16)

式中:ErIr为钢轨的抗弯刚度;l为钢轨长度;xi和xj分别为第i、j个扣件节点与左端支座的距离,xi=i·ls;aj=xj;bj=l-xj;ls为扣件之间的间距。

对于扣件系统,各扣件节点处的扣件力为:

Pi=kp(wri-wbi)

(17)

式中:kp为钢轨扣件刚度;wbi为叠合梁在第i个扣件节点处的变形。

联立式(12)、式(13)、式(15)、式(17),可得:

(kP+dN×N+fN×N)PN=-wN

(18)

式中:kp=(1/kp)E,E为单位矩阵;dN×N、fN×N分别为dij、fij组成的矩阵;PN为各个节点处扣件力组成的矩阵;wN为叠合梁在各节点处的变形组成的矩阵。

通过式(18)求得的扣件力PN,代入式(15)可得到钢轨的垂向变形,代入式(12)可得到叠合梁的垂向变形。需要指出的是,由于在不均匀沉降区域路基结构刚度不均匀,导致轨道与路基的变形不协调,在沉降中心区域易出现局部界面脱粘情况,此时,二者接触状态变得复杂。在局部脱粘区域,轨道与路基处于分离状态,二者间无接触,在沉降范围内的非脱粘区轨道与路基保持紧贴,在整个沉降区域内,轨道与路基间的接触并不连续,此状态下存在接触非线性,尤其是在局部脱粘区域,轨道与路基间的接触非线性明显。

1.2 考虑接触非线性的轨道梁-体有限元模型

路基沉降较大时,可能发生轨下离缝空吊现象,使轨道结构层与路基表层间存在接触非线性。为充分研究轨道结构与路之间的接触非线性问题,基于有限元方法建立轨道梁-体空间模型,如图4。

图4 双块式无砟轨道梁-体有限元模型Fig. 4 Beam-body finite element model of double block ballastless track

模型中,钢轨用BEAM188梁单元模拟,扣件用COMBIN14弹簧阻尼单元模拟,其他轨道结构采用连续实体结构模型,以SOLID185实体单元模拟。道床板与支承层间以及双块式轨枕与道床板间均采用共节点方式。考虑到轨道支承层和路基间可能出现离缝、脱空现象,采用TARGE170和CONTA174接触单元来模拟支承层和路基表面的接触。弹簧扣件的垂向刚度取3×107N/m,双块式无砟轨道其他结构参数取值见表1。

表1 双块式无砟轨道及路基相关参数取值Table 1 Relative parameters of double-block ballastless track and subgrade

为考虑沉降的作用范围并尽量降低边界效应带来的影响,轨道模型长度取60 m。路基纵向不均匀沉降通过在路基表面施加位移余弦荷载来实现,同时对上部轨道结构施加自重荷载,使之能够产生跟随性变形,最后除去由重力作用引起的轨道变形,可得到完全由路基沉降作用而产生的变形。

2 模型验证

为了验证所提方法的准确性,以文献[15]中兰新线高速铁路线路在路基不均匀沉降区域,轨道轨面不平顺实测数据来验证,文献中路基不均匀沉降工况为10.5 mm/40 m[15]。图5为笔者解析方法与有限元模拟出的轨面变形结果及实测数据的对比图。由图5可知,解析模型预测轨面变形结果与实测结果较吻合,与有限元模拟的结果几乎一致,证明笔者解析方法具有可靠性与准确性。

图5 不同求解模型下沿线路纵向的轨面变形Fig. 5 Rail surface deformation along the longitudinal direction of the line under different solution models

3 结果与讨论

基于双块式无砟轨道Winkler地基叠合梁解析模型和梁-体空间有限元模型,对比分析典型波长下,不同沉降幅值的轨面变形,如图6。图6(a)是5mm(沉降幅值)/20 m(波长)工况下,2种模型的轨面变形计算结果对比;图6(b)是沉降幅值增加到20 mm 时2种模型的轨面变形结果。

图6 不同沉降幅值下2种模型的轨面变形计算结果对比Fig. 6 Calculation results comparison of rail surface deformation of two kinds of models with different settlement amplitudes

由图6可知,当路基沉降幅值为5 mm时,2种模型计算的轨面变形结果几乎一致,当路基沉降幅值为20 mm时,2种模型结果差异较大,有限元模型结果明显小于解析模型结果。同时,从图6可以判断出,沉降波长一定时,随着沉降幅值的增加,2种模型计算结果从高度吻合变化到有较大差异,在此过程中必然存在一个临界沉降幅值,使得2种模型的计算结果刚好基本相等,即轨道与路基接触非线性触发的临界条件,超过此临界沉降幅值,解析模型的计算结果开始出现偏差(相差超过1%)。

图7(a)是路基沉降20 mm/20 m工况下轨道-路基纵向接触力有限元模拟结果,图7(b)是对应的轨道-路基变形云图。由图7可知:此工况下轨道结构与路基层之间存在明显的空隙,此区域轨道和路基间的接触应力为0,轨道和路基间存在接触失效行为,因此沉降区域中轨道实际挠度小于Winkler地基叠合梁模型预测结果。

图7 20 mm/20 m工况下轨道-路基接触力和变形云图Fig. 7 Contact force and deformation nephogram of track-subgrade contact force under condition of 20 mm/20 m

轨道与路基接触非线性触发的临界条件是指使轨道与路基在沉降中心区域由原来的一种接触状态转变为另一种接触状态的临界点。图8为沉降波长20 m条件下,有限元模拟轨道-路基在沉降中心接触力随沉降幅值变化的结果。由图8可知:当沉降波长为20 m且沉降幅值小于10 mm时,轨道与路基在沉降中心的接触力随沉降幅值的增大线性减小,当沉降幅值刚好达到10 mm后,轨道与路基在沉降中心的接触力变为0,随着沉降幅值继续增大,二者间的接触力始终为0,原来的线性接触状态转变为另一种线性接触状态,此变化过程就是一种非线性行为,在转折点处认为是接触非线性触发的临界状态。

为快速给出路基不均匀沉降工况下轨面变形的预测结果,有必要确定轨道与路基接触非线性触发的临界条件。以波长10 m为例,图9(a)描述了不同沉降幅值下2种模型计算的钢轨最大挠度(弯沉)结果。当沉降幅值小于1 mm时,2种模型预测的钢轨最大挠度吻合得很好,沉降幅值继续增大,Winkler叠合梁模型预测结果大于有限元模型,并随沉降幅值增大到1.2 mm时偏差接近5%,当偏差超过5%认为叠合梁解析模型不再适用。图9(b)是沉降波长10 m沉降幅值1mm时,2种模型沿纵向的轨面变形计算结果对比,由图9(b)可以看出2种模型的计算结果几乎完全一致,由此可确定沉降波长为10 m时,Winkler地基叠合梁解析模型应用的临界沉降幅值为1 mm。同样可以确定沉降波长为15、20、25 m时,解析模型对应的临界沉降幅值分别为3、10、30 mm。

图9 沉降波长分别为10、15、20、25 m时2种模型预测的沉降幅值与钢轨弯曲变形关系Fig. 9 The relationship between the predicted settlement amplitude and the bending deformation of the steel rail of the two kinds of models with the settlement wavelengths of 10 m, 15 m, 20 m and 25 m respectively

余弦型路基不均匀沉降通常会导致轨道结构在沉降边缘区域出现微小的局部上拱现象,且局部上拱现象在沉降波长为25 m,沉降幅值在30 mm之后较为显著[16]。由图9(h)可知,对于路基沉降范围为25 m,沉降幅值为30 mm的工况,虽然2种模型的计算出的轨面变形结果吻合度很高,但由于沉降幅值较大,导致钢轨在沉降边缘区域局部上拱幅值(1.12 mm)较大、非线性增强,而解析模型不能很好捕捉非线性,在此上拱区域解析模型的结果存在些许偏差。

图10为临界沉降幅值随上述4种典型波长变化的趋势。由图10可知,临界沉降幅值随着沉降波长的增大呈现增大趋势,且增长的幅度逐渐变大,整体呈高次函数增长变化。

图10 Winkler地基叠合梁沉降波长-临界沉降幅值曲线Fig. 10 Settlement wavelength-critical settlement amplitude curves for Winkler foundation composite beam

4 结 论

笔者建立Winkler弹性地基叠合梁解析模型,求解双块式无砟轨道在下凹余弦型路基不均匀沉降下的轨面变形。同时,建立考虑轨道与路基间接触非线性的轨道梁-体有限元模型对比分析解析模型的适用性及应用范围:

1)小沉降幅值/波长比时,Winkler弹性地基叠合梁解析模型预测结果与有限元模拟结果一致。随着沉降幅值/波长比增大,Winkler弹性地基叠合梁模型高估了轨道梁的真实弯曲变形,偏差越来越大。

2)路基不均匀沉降波长为10、15、20、25 m时,叠合梁解析模型应用的临界沉降幅值分别为1、3、10、30 mm,小于临界沉降幅值时,解析模型预测轨道变形结果是完全可靠的。

3)在较小沉降波长时,轨道支承层与路基易发生脱空现象,临界沉降幅值应严格限制。

4)随着沉降波长的增长,临界沉降幅值呈高次函数增长。