多自变量的交互作用对因变量的影响

2023-07-11宋荣荣范亚茹

西南民族大学学报（自然科学版） 2023年3期

宋荣荣，范亚茹

(西南民族大学数学学院，四川成都 610041)

在众多应用中，因变量与自变量的关系是非常复杂的.研究多个自变量与因变量之间的关系，就不得不考虑自变量之间的交互作用，因为交互作用会严重影响自变量与因变量的关系[1-5].不排除交互作用的干扰，会出现什么问题呢? 交互作用会造成因变量和自变量之间相关关系的偏倚，导致因变量与自变量之间的任何一种相关程度增大或减少[6-8].特别是当因变量和自变量不相关时，由于交互作用还会导致它们之间存在假的相关性[9].如何排除交互作用研究多自变量与因变量间的关系，是当前大学生在学习过程中亟待解决的问题. 在参加数学建模竞赛时，大多数学生并不清楚如何排除交互作用，再研究多个自变量对因变量的影响[10-11].因此，教会学生如何排除交互作用的干扰，研究多个自变量对因变量的影响是至关重要的[12].

目前，排除交互作用的主要方法是多因素调整分析法[13].当问题中交互作用较多，且交互作用复杂时，可采用多因素调整分析法[14]. 在该方法中，根据因变量的类型，可选择三种回归模型:多重线性回归、logistic 回归及Cox 回归.其中多重线性回归的因变量是连续变量，logistic 回归的因变量是分类变量，而Cox 回归的因变量是时间变量.本文以2022 年全国大学生数学建模竞赛C 题为例，研究玻璃文物风化与纹饰、颜色及类型之间的关系.因为风化是分类因变量，所以选用logistic 回归排除交互作用的干扰，并研究多自变量与因变量的关系.

本文将基于SPSS 软件建立logistic 回归模型，为学生提供一种层层递进的探究方法，让学生掌握如何排除交互作用的干扰研究多个自变量与因变量之间的关系，如何利用软件探究自变量之间的交互作用，如何深入地分析交互作用对变量间相关关系的影响.

1 问题分析与模型假设

以2022 年高教社杯全国大学生数学建模竞赛C题为例，探究古代玻璃制品的成分分析与鉴别. 由于古代玻璃很容易因为埋藏环境的影响而导致风化，而且在风化过程中，外部环境元素与玻璃内部元素进行化学反应而大量地交换，导致玻璃的成分比例发生改变，继而影响对玻璃类别的正确判断. 现有一批我国古代玻璃制品的相关数据，需要分析玻璃文物表面风化和颜色、玻璃类型以及纹饰的关系.

这个题目包括54 件古代玻璃文物，每件玻璃文物都有具体的分类信息，原始数据如表1 所示.

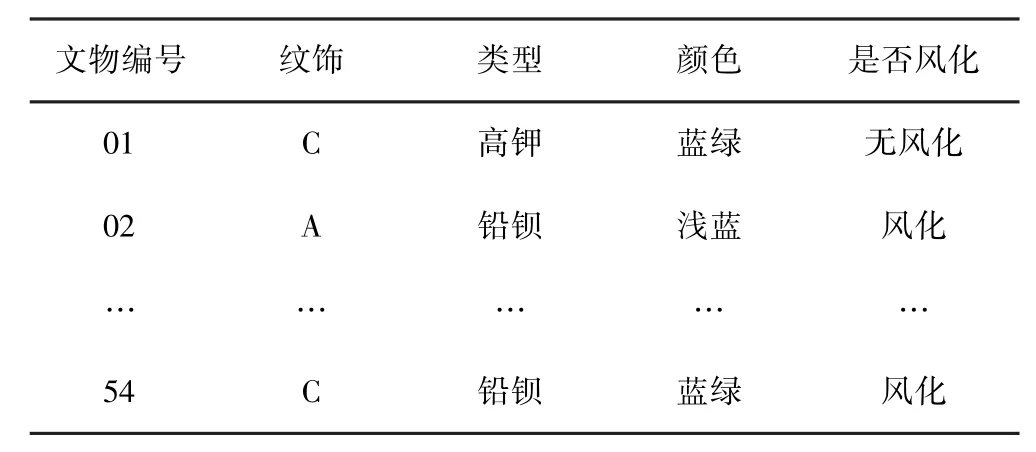
表1 54 件玻璃文物的分类信息Table 1 Classification information of 54 glass cultural relics

为更好的进行相关性分析，本文分别对表1 中“颜色”和“表面风化”两个变量进行数据化处理，处理结果如表2 所示. 我们用1 到9 分别表示浅蓝、蓝绿、深绿、紫、浅绿、黑、深蓝、绿色.用1 表示玻璃文物被风化，0 表示未风化.

表2 变量数据表Table 2 The table of variable data

为了研究文物样品表面风化与颜色、玻璃类型以及纹饰间的关系. 首先，我们对所有变量进行相关性分析；其次，运用统计软件SPSS27.0，建立了7 种logistic 模型，得到显著性结果并进行分析；最后，根据显著性的结果，排除交互作用的影响，给出风化与颜色、玻璃类型以及纹饰间的变量关系.

2 Logistic 回归模型建立

2.1 模型假设

假设1:文物相互独立；

假设2:文物的风化情况服从二项分布；

2.3 子宫内膜组织实时荧光定量PCR检测两组患者ER、PR 的表达水平比较与对照组比较，宫腔粘连组患者ER 、PR蛋白表达水平均较高，两组比较差异有统计学意义(P<0.05)。见表4。

假设3:π(xi)与xi有关，表示第i个文物发生风化的概率，简记为πi.

定义为:

logistic 回归不假设自变量与因变量之间存在直接的线性关系，而是通过链接函数建立线性关系，如

假设4:假设文物形状对结果没有显著性影响；

假设5:假设只有颜色、纹饰和类别对风化有影响，不考虑其他因素对风化有重要影响.

2.2 模型建立

设风化的情况记为Y(Y ＝1 表示文物已风化，Y＝0 表示文物未风化)，每件文物由若干指标表示其特征，记为X，如X1是类型，X2是颜色，X3是纹饰.xi表示第i个文物的特征观测值，xi1表示第i个文物的类型值，xi2表示第i个文物的颜色值，xi3表示第i个文物的纹饰值，yi表示第i个文物的风化结果(i ＝1，2，…，54) ，β0是常数项，β1，β2，β3是logistic 模型回归系数，π(xi)的取值范围是[0，1] .

我们层层递进，深入分析了三个自变量类型、颜色、纹饰对因变量风化的关系.首先，不排除三个自变量的交互作用，探究每个自变量对因变量的影响；其次，排除任意两个自变量之间的交互作用，探究每个自变量对因变量的影响；最后，排除三个自变量之间的交互作用，探究三个自变量对因变量的影响. 本文总共建立了7 个logistic 模型[15]，如下所示.

1)不排除交互作用，建立每个自变量对因变量的影响模型.

模型一:不排除纹饰和颜色的交互作用，建立类型对风化的影响模型.

设风化情况为Y，每件文物的特征为X ＝X1，则在第i个文物X ＝xi ＝xi1的条件下，风化(yi ＝1 )的条件概率为:

模型二:不排除类型和纹饰的交互作用，建立颜色对风化的影响模型.

设风化情况为Y，每件文物的特征为X ＝X2，则在第i个文物X ＝xi ＝xi2的条件下，风化(yi ＝1 )的条件概率为:

模型三:不排除类型和颜色的交互作用，建立纹饰对风化的影响模型.

设风化情况为Y，每件文物的特征为X ＝X3，则在第i个文物X ＝xi ＝xi3的条件下，风化(yi ＝1 )的条件概率为:

2)排除任意两个自变量之间的交互作用，探究剩余自变量对因变量的影响.

模型四:排除颜色和类型的交互作用，建立类型对风化的影响模型.

设风化情况为Y，每件文物的特征为X ＝(X1，X2) ，则在第i个文物X ＝xi ＝(xi1，xi2)的条件下，风化(yi ＝1 )的条件概率为:

模型五:排除纹饰和类型的交互作用，建立类型对风化的影响模型.

设风化情况为Y，每件文物的特征为X ＝(X1，X3) ，则在第i个文物X ＝xi ＝(xi1，xi3)的条件下，风化(yi ＝1 )的条件概率为:

模型六:排除纹饰和颜色的交互作用，建立颜色对风化的影响模型和纹饰对风化的影响模型.

设风化情况为Y，每件文物的特征为X ＝(X2，X3) ，则在第i个文物X ＝xi ＝(xi2，xi3)的条件下，风化(yi ＝1 )的条件概率为:

3)排除三个自变量之间的交互作用，建立三个自变量对风化的影响模型.

模型七:排除纹饰和颜色的交互作用，建立类型对风化、纹饰对风化和颜色对风化的影响模型.

设风化情况为Y，每件文物的特征为X ＝(X1，X2，X3) ，则在第i个文物X ＝xi ＝(xi1，xi2，xi3)的条件下，风化(yi ＝1 )的条件概率为:

其中，logistic 回归模型主要采用极大似然法估计4 个未知参数β0，β1，β2，β3.

2.3 模型求解和结果分析

利用表2 的数据，运用SPSS27.0 软件，得到logistic 模型中的参数的最大似然估计值，模型一的结果如表3 所示.

表3 不排除纹饰和颜色的交互作用下类型对风化的模型结果(模型一)Table 3 Model results of the type on the weathering with the interaction of texture and color (Model I)

由表3 知，类型的显著性值为0.024，小于置信水平0.05，所以在纹饰和颜色的交互作用下，类型对风化在统计学意义上有显著性影响；Odds Ration (OR)值为0.250，表明高钾发生风化的可能性与铅钡发生风化可能性之比是0.25，铅钡更容易发生风化.在纹饰和颜色的交互作用下，类型对风化的影响模型为:

lnπ(xi)＝β0＋β1xi1＝0.693-1.386xi1.

从模型二到模型七的显著性结果如表4 到表9所示.当显著性值大于置信水平0.05 时，表明该变量对因变量的影响不显著；反之，显著性值小于置信水平0.05 时，表明该变量对因变量的影响显著，且显著性值越小表明影响越显著.

表4 不排除类型和纹饰的交互作用下颜色对风化的模型结果(模型二)Table 4 Model results of the color on the weathering with the interaction of type and decoration (Model II)

由表4 到表9 知，模型二到模型七的显著性结果都大于置信水平0.05，说明从模型二到模型七，模型的自变量对因变量在统计学意义上没有显著性影响.

另外，由表9 中每个自变量的参数估计值的绝对值大小知，对风化影响最重要的前三种特征是:黑色(62.034)，蓝绿色(59.352)和高钾( -56.391)，其中黑色和蓝绿色对风化是正相关影响，高钾对风化是负相关影响.由表3 中的显著性结果(0.024)知，考虑其他自变量交互作用时，类型对风化有显著性影响；由表6 ～表9 中的显著性结果知，不考虑其他自变量交互作用时，类型对风化没有显著性影响.由表4、表5、表8 和表9 中的显著性结果知，考虑和不考虑其他自变量交互作用时，颜色和纹饰对风化都没有显著性影响.

表5 不排除类型和颜色的交互作用下纹饰对风化的模型结果(模型三)Table 5 Model results of the decoration on the weathering with the interaction of type and color (Model III)

表6 排除颜色和类型的交互作用下类型对风化的模型结果(模型四)Table 6 Model results of the type on the weathering without the interaction of color and type (Model IV)

表7 排除纹饰和类型的交互作用下类型对风化的模型结果(模型五)Table 7 Model results of the type on the weathering without the interaction of decoration and type (Model V)

表8 排除任意两个自变量的交互作用下自变量对风化的模型结果(模型六)Table 8 Model results of the independent variables on the weathering without the interaction of any two independent variables (Model VI)

表9 排除三个自变量的交互作用下自变量对风化的模型结果(模型七)Table 9 Model results of the independent variables on the weathering without the interaction of three independent variables (Model VII)

综上所述，通过讨论自变量间的交互作用，本文探究了多个自变量对因变量的影响，获得了7 个自变量和因变量的关系模型. 从7 个关系模型中，发现模型一是最能表示3 个自变量和因变量之间的关系.