一个无安全信道的无证书公钥可搜索加密方案
2023-07-11孙莹莹刘晓光刁颖颖谯小康
孙莹莹,刘晓光,,刁颖颖,谯小康
(1.西南民族大学计算机科学与工程学院,四川 成都 610041;2.广西密码学与信息安全重点实验室,广西 桂林 541004;3.西南民族大学数学学院,四川 成都 610041)
众所周知,加密技术可以增强数据的安全性,却限制了用户对数据的高效搜索和共享.一个不理想的解决方案是用户首先下载所有加密数据,待全部解密后进行搜索操作.但随着数据规模的不断增大,计算和通信成本会呈指数级增加.为解决这个问题,基于对称加密的可搜索方案首先被提出[1].然而,一个棘手问题是如何秘密地将密钥分发给授权用户[2].此外,该类方案不可避免地会消耗大量的计算和通信成本.
2004 年,Boneh 等人[3]给出了第一个PEKS 方案.此方案实现了Bob 通过云服务器向Alice 发送文档,具体过程如下:Bob 首先从文档中提取关键字,并用Alice 的公钥加密,生成关键字密文并上传至服务器.Alice 使用其私钥加密关键字生成陷门,并将生成的陷门发送至服务器.最后,服务器对接收到的关键字密文和陷门进行测试.如果二者包含的关键字相同,服务器将把包含该关键字的文档发送给Alice.然而,Baek 等人[4]指出方案[3]为了保证陷门的安全性,需要通过高消耗的安全信道将陷门传输至服务器.因此,他们提出了一个无安全信道的PEKS 方案(SCF-PEKS).该方案中,云服务器的公、私钥分别参与密文的生成与测试算法.Yau 等人[5]指出方案[4]容易受到离线关键字猜测攻击.这是因为用户通常使用常见的关键字来进行搜索操作,关键字是在一个很小的空间中选择的[6].Rhee 等人[7]设计了一个增强的SCF -PEKS 方案,但此方案只考虑了外部关键字猜测攻击(OKGA),却不能抵抗内部关键字猜测攻击(IKGA).Xu 等人[8]提出了模糊关键字PEKS 方案.在该方案中,每个关键字对应一个精确的关键字搜索陷门和一个模糊的关键字搜索陷门,但该方案也只能抵抗OKGA.
Lu 等人[9]提出了一个基于证书的SCF-PEKS 方案.此方案可有效抵抗IKGA,却引入了繁琐的证书管理问题.Li 等人[10]提出了一个基于身份的SCF-PEKS 方案.该方案解决了证书管理问题,却存在密钥托管问题.Pakniat[11]提出了一个无证书的SCF-PEKS 方案,有效地解决了证书管理和密钥托管问题.然而,Miao 等人[12]指出,大多数现有的PEKS 方案仍然容易受到IKGA 攻击,这意味着内部敌手可以成功地猜测出候选关键字.2019年,Zhang 等人[13]提出了无证书公钥认证的SCF-PEKS 方案.2021 年,Lu 等人[14]提出了轻量级公钥认证PEKS方案.此类基于认证的方案通过验证发送者的身份,可有效抵抗IKGA 和OKGA.
遗憾的是,现有的许多无安全通道PEKS 方案都依赖于高消耗的双线性对.本文中,我们将提出一个无证书轻量级可认证的无安全信道PEKS 方案(SCF-PAEKS),主要贡献如下:1)方案基于无证书密码学,不存在证书管理和密钥托管问题;2)使用标量乘法代替高成本的双线性对,具有更高的效率;3)为了增强方案的安全性,我们在加密方案中不仅输入数据接受者的公钥,还输入数据拥有者的公钥,使得数据接收者可以验证数据拥有者的身份;4)对所推出的方案进行了性能分析,并在随机预言模型下证明了方案的安全性.
1 预备知识
下面将给出本文算法安全性所基于的困难问题和基本系统模型.
1.1 椭圆曲线Diffie-Hellman 问题
设G是椭圆曲线上的点组成的加法循环群,其阶数为素数q.P是G的生成元.下面将分别给出椭圆曲线Diffie-Hellman (CDH) 问题和决策Diffie-Hellman (DDH) 问题的定义.定义1 (CDH):给出三元组(P,aP,bP) ∈G,其中a,b∈Zp
*,计算abP是困难问题.定义2 (DDH):给出四元组(P,aP,bP,cP) ,其中a,b,c∈Zp
* ,确定c是否等于ab是困难问题.
1.2 系统模型
如图1 所示,SCF-PAEKS 方案的系统模型主要由四个实体组成:密钥生成中心(KGC)、云服务器、数据拥有者和数据接收者.每个实体的工作方式如下:
1) KGC:它是一个半可信的第三方,可以生成系统主密钥以及数据拥有者、数据接收者和云服务器的部分私钥.同时,KGC 负责公布系统参数.
2)数据拥有者:他/她的加密信息分为两部分.首先,他/她使用自己的私钥加密数据并生成密文,同时从数据中提取关键词.其次,数据拥有者使用提出的SCF-PAEKS 方案对关键字进行加密,生成关键字密文,并将密文上传到云服器.
3)数据接收者:他/她使用其私钥、数据拥有者的公钥和云服务器的公钥为他/她想要搜索的关键字生成陷门,并将陷门发送给云服务器.
4)云服务器:存储和处理数据的半可信第三方.它利用自己的私钥测试数据所有者发送的关键字密文与数据接收者发送的陷门.如果二者包含相同的关键字,它会将相应的信息返回给数据接收者.
2 SCF-PAEKS 方案
该方案由以下八个多项式时间算法组成. 我们分别定义数据拥有者、数据接收者和云服务器的身份为IDO、IDR和IDS.算法中所使用的符号见表1.

表1 符号定义Table 1 Symbol definition
2.1 初始化
给定一个安全参数λ,KGC 选择一个阶为q的加法循环群G,P是G的生成元.KGC 选择随机值s∈Zq*作为系统主密钥,并计算Ppub=sP作为系统公钥.KGC 选择三个不同的哈希函数:H1:{0,1}*×G→Zq*,H2:G × G ×G × G ×G→{0,1}*,H3:{0,1}*×{0,1}*→Zq*.KGC 保密系统主密钥s,并公开系统参数params={λ,G,q,P,Ppub,H1,H2,H3} .
2.2 设置部分私钥
KGC 将执行以下步骤:
1)输入数据拥有者的身份IDO∈{0,1}*.KGC 选择随机值rIDO∈Zq*计算,并计算QIDO=rIDOP,μIDO=H1(IDO,QIDO) ,和dIDO=rIDO +sμIDO(modq) .KGC 返回QIDO,μIDO和dIDO给数据拥有者.
2)输入数据接收者的身份IDR∈{0,1}*. KGC 选择随机值rIDR∈Zq*,并计算QIDR=rIDRP,μIDR=H1(IDR,QIDR) 和dIDR=rIDR +sμIDR(modq) .KGC 返回QIDR,μIDR和dIDR给数据接收者.
3)输入云服务器的身份IDS∈{0,1}*.KGC 选择随机值rIDS∈Zq*,并计算QIDS=rIDSP,μIDS=H1(IDS,QIDS) 和dIDS=rIDS +sμIDS(modq) .KGC 返回QIDS,μIDS和dIDS给云服务器.
2.3 设置秘密值
输入IDO∈ {0,1}*,IDR∈ {0,1}*和IDS∈ {0,1}*.
1)数据拥有者选择随机值xIDO∈Zq*作为自己的秘密值.
2)数据接收者选择随机值xIDR∈Zq*作为自己的秘密值.
3)云服务器选择随机值xIDS∈Zq*作为自己的秘密值.
2.4 设置私钥
1)数据拥有者设置SKIDO=(SKIDO1,SKIDO2) =(xIDO,dIDO) 作为自己的私钥.
2)数据接收者设置SKIDR=(SKIDR1,SKIDR2) =(xIDR,dIDR) 作为自己的私钥.
3)云服务器设置SKIDS=(SKIDS1,SKIDS2) =(xIDS,dIDS) 作为自己的私钥.
2.5 设置公钥
输入系统参数params,并分别输入数据拥有者的秘密值,数据接收者的秘密值和云服务器的秘密值xIDO,xIDR和xIDS.
1)数据拥有者计算YIDO=xIDOP,将PKIDO=(PKIDO1,PKIDO2) =(YIDO,QIDO) 设置为自己的公钥.
2)数据接收者计算YIDR=xIDRP,将PKIDR=(PKIDR1,PKIDR2)=(YIDR,QIDR) 设置为自己的公钥.
3)云服务器计算YIDS=xIDSP,将PKIDS=(PKIDS1,PKIDS2)=(YIDS,QIDS) 设置为自己的公钥.
2.6 SCF-PAEKS 方案
输入params,SKIDO,PKIDR和PKIDS.数据拥有者按照下列步骤加密关键字w:
1)数据拥有者选择随机值r1∈Zq*.
2)数据拥有者计算:
数据拥有者返回C =(C1,C2,C3) .
2.7 陷门
输入params,SKIDR,PKIDO和PKIDS.数据接收者按照如下步骤生成陷门Tw:
1)数据接收者选择随机值r2∈Zq*.
2)数据接收者计算:
数据接收者返回陷门Tw'=(T1,T2,T3) .
2.8 测试
输入params,Tw', SKIDS和关键字密文C. 云服务器验证等式C2(xIDS +dIDS)- C3=T2(xIDS +dIDS)+T3((xIDS +dIDS)-1-1)- T1是否成立.如果成立,输出1,否则,输出0.
正确性验证:Tw
′是关键字w′的陷门,w是密文C中的关键字.我们知道
和
由于θ1=θ2,故若w =w′,则K1=K2.因此有:
3 安全证明
在本节中,我们首先给出SCF-PAEKS 方案的安全模型.随后对所提出方案进行安全性分析.分析结果表明,在随机预言模型下,该方案可有效抵抗IKGA 且此方案满足密文不可区分性.
3.1 安全模型
在无证书密码系统的自适应性选择密文攻击游戏中,我们定义了挑战者C分别与外部敌手A1 ,内部敌手A2 之间的攻击博弈.外部敌手A1 可以任意替换用户的公钥,但不能获取系统主密钥.内部敌手A2 ,通常指半可信云服务器.它可以获得系统主密钥,但不能替换用户的公钥.
游戏1:这是一个挑战者C与外部敌手A1 之间的互动.
初始化:给定安全参数λ,C运行系统算法产生参数params和系统主密钥s.C保密s,并把params发送给A1 .
哈希查询:C允许A1 查询哈希预言并返回哈希值.
部分私钥查询:A1 对身份ID 进行查询,C计算该身份的部分私钥dID并将其返回给A1 .
私钥查询:A1 对身份ID 进行查询,C计算相应的私钥SKID返回给A1 .
公钥查询:A1 对身份ID 进行查询,C将相应的公钥PKID返回给A1 .
替换公钥查询:A1 选择新的公钥PK ′ID用于替换原始公钥PKID.
陷门查询:A1 对身份IDO、IDS及关键字w进行查询,C生成陷门Tw并返回给A1 .
挑战:A1 选择未执行过陷门查询的w0和w1作为挑战关键字.C随机选择b′∈{0,1} ,然后通过执行算法生成关键字密文wb并发送给A1 .
更多查询:A1 可继续执行以上阶段查询(w0和w1陷门查询除外).
猜测:A1 给出猜测结果b′∈{0,1} .若b′ =b,则A1 挑战成功.A1 挑战成功的优势定义为:
游戏2:这是一个挑战者C与内部敌手A2 之间的互动.
初始化:给定安全参数λ,C运行系统算法产生参数params和系统主密钥s,并把它们发送给A2 .查询:除提取私钥查询和替换公钥查询外,A2 可执行与游戏1 相同的查询.
挑战:A2 选择未执行过陷门查询的w0和w1作为挑战关键字.C随机选择b′∈{0,1} ,然后通过执行算法生成关键字密文wb并发送给A2 .
更多查询:A2 可继续执行以上阶段询问(w0和w1陷门查询除外).
猜测:A2 给出猜测结果b′∈{0,1} .若b′ =b,则A2 挑战成功.A2 挑战成功的优势定义为:
定义3:如果没有敌手以不可忽略的优势Adv(A1) 和Adv(A2) 赢得游戏,说明所提出的SCF-PAEKS 方案在抵抗IKGA 时是语义安全的.
3.2 证明
定理1:假设CDH 是困难问题,则所提出的SCF-PAEKS 方案在随机语言模型中是语义安全的.这个定理可由以下两个引理证明.
引理1:假设有一个外部敌手A1 以不可忽略的优势ε赢得SCF-PAEKS 方案.我们必须构造一个算法C以不可忽略优势:
来解决CDH 问题, 其中qH1,qE,qS,qT分别表示H1查询,部分私钥查询,秘密值查询,陷门查询的最大查询次数.
证明:假设(P,aP,bP) 是CDH 问题随机生成的一个实例,那么算法C通过与敌手A1 交互来模拟挑战者.
初始化:C随机选择IDI( 1 ≤I≤qH1)作为挑战者身份.然后C执行算法计算系统公钥Ppub=aP和系统参params ={λ,G,q,P,Ppub,H1,H2,H3}.最后,C返回params给A1 .
H1查询:C维护一张LH1列表(IDi,QIDi,μIDi) ,当收到A1 关于(IDi,QIDi) 的查询时,若(IDi,QIDi,μIDi) 已存在于LH1,则C返回μIDi.否则,C选择随机值μIDi∈Zq*,将其返回给A1 ,并将(IDi,QIDi,μIDi) 加入LH1.
H2查询:C维护一张LH2列表(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) ,当收到A1 关于(SKIDj1·PKIDi1,PKIDj,PKIDi)的查询时,若(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) 已经存在于LH2,则C返回θi.否则,C随机选择θi∈Zq*,将其返回给A1 ,并将(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) 加入LH2.
H3查询:C维护一张LH3列表(wi,θi,ki) ,当收到A1 关于(wi,θi) 的查询时,若(wi,θi,ki) 已经存在于LH3,则C返回ki.否则,C随机选择ki∈Zq*将其返回给A1 ,并将(wi,θi,ki) 加入LH3.部分私钥查询:C维护一张Lp1列表(IDi,QIDi,dIDi) .当收到A1 关于IDi的查询时,若IDi =IDI,C终止算法(这个过程由E1表示).否则,C随机选择dIDi∈Zq*,将其返回给A1 ,并将(IDi,QIDi,dIDi) 加入Lp1.
秘密值查询:C维护一张Lp2列表(IDi,xIDi) .当收到A1 关于IDi的查询时,若IDi =IDI,C终止算法(这个过程由E2表示).否则,C随机选择xIDi∈Zq*,并查询Lp1列表(IDi,QIDi,dIDi) .最后,C将SKIDi =(xIDi,dIDi)返回给A1 ,并将(IDi,xIDi) 加入Lp2.
提取公钥查询:C维护一张Lp3列表(IDi,QIDi,YIDi) .当收到A1 关于IDi的查询时,若(IDi,QIDi,YIDi) 已经存在于Lp3,C返回PKIDi =(QIDi,YIDi) .否则,C分别查询LH1列表(IDi,QIDi,μIDi) 和Lp2列表(IDi,xIDi) ,并计算YIDi =xIDiP.最后,C返回PKIDi =(QIDi,YIDi) 给A1 ,并将(IDi,QIDi,YIDi) 加入Lp3.
公钥替换查询:当收到A1 关于(IDi,QIDi,YIDi) 查询时,C分别用和去替换QIDi和YIDi,并更新Lp3列表(IDi,QIDi,YIDi) .
陷门查询:当收到A1 关于IDi的陷门查询时,若IDi =IDI,C终止算法(这个过程由E3表示).否则,C随机选择r2∈Zq*并计算T2=r2P.然后,C查询LH3列表(wi,θi,ki) 和LH2列表(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) ,计算K2=H3(ki,θi) 、T2=(K2+r2) SKIDi2-1(PKIDi2+αIDiPpub) 和T3=r1(YIDS +QIDS +μIDSPpub) .最后,C返回Tw'=(T1,T2,T3) 给A1 .
挑战:A1 给出身份为ID*的挑战关键字w0和w1.若ID*≠IDI,C终止算法(这个过程由E4表示).否则,C首先选择随机值r1∈Zq*并计算C1=r1P.然后,C查询LH3列表(wi,θi,ki) 和LH2列表(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) ,计算K1=H3(ki,θi)、C2=C1+K1·SKIDO2-1(PKIDO2+μIDOPpub) 和C3=r2(YIDS +QIDS +μIDSPpub) .最后,C返回C =(C1,C2,C3) 给A1 .
更多查询:A1 可继续执行以上阶段除挑战关键字w0和w1之外(这个过程由E5表示)的自适应查询.
猜测:A1 给出猜测结果b′∈{0,1} .C设置C1=bP,如果b((C2-T2+T1)(xIDS +dIDS)-C1(xIDS +dIDS)+Ppub)=abP成立,则说明C可以解决CDH 问题.
只有当E1,E2,E3,E4,E5事件之一发生时,游戏才会中止.下面将对C解决CDH 问题的优势ε′进行分析.首先:
和
故有Pr[┐E5] ≥ 2Pr[b′ =b |-1≥2ε,因此:
引理2:假设有一个内部敌手A2 以不可忽略的优势ε赢得SCF-PAEKS 方案.必须构造一个算法C以不可忽视优势:
来解决CDH 问题,其中qH1,qE,qS,qT分别表示H1查询,部分私钥查询,秘密值查询,陷门查询的最大查询次数.
证明:假设(P,aP,bP) 是CDH 问题随机生成的一个实例,那么算法C通过与敌手A2 交互来模拟挑战者.
初始化:C随机选择IDI( 1 ≤I≤qH1)作为挑战身份.然后C执行算法,随机选择s∈Zq*,并计算系统公钥Ppub=sP和系统参params ={λ,G,q,P,Ppub,H1,H2,H3} .最后,C返回s和params给A2 .
H1查询:C维护一张LH1列表(IDi,QIDi,μIDi) ,当收到A2 关于(IDi,QIDi) 的查询时,若(IDi,QIDi,μIDi) 已存在于LH1,则C返回μIDi.否则,C选择随机值μIDi∈Zq*将其返回给A2,并将(IDi,QIDi,μIDi) 加入LH1.
H2查询:C维护一张LH2列表(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) ,当收到A2 关于(SKIDj1·PKIDi1,PKIDj,PKIDi)的查询时,若(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) 已经存在于LH2,则C返回θi.否则,C随机选择θi∈Zq*,将其返回给A2 ,并将(SKIDj1·PKIDi1,PKIDj,PKIDi,θi) 加入LH2.
H3查询:C维护一张LH3列表(wi,θi,ki) ,当收到A2 关于(wi,θi) 的查询时,若(wi,θi,ki) 已经存在于LH3,则C返回ki.否则,C随机选择ki∈Zq*将其返回给A2 ,并将(wi,θi,ki) 加入LH3.
部分私钥查询:C维护一张Lp1列表(IDi,YIDi,xIDi) ,当收到A2 关于IDi的查询时,C随机选择xIDi∈Zq*并计算YIDi =rIDiP.然后,C查询LH1列表(IDi,QIDi,μIDi) ,计算dIDi =rIDi +sμIDi,并将rIDi和dIDi返回给A2 .最后,C将(IDi,QIDi,dIDi) 加入Lp1.
提取公钥查询:C维护一张Lp2列表(IDi,QIDi,YIDi) .当收到A2 关于IDi的查询时.若(IDi,QIDi,YIDi) 已经存在于Lp2,则C返回PKIDi =(QIDi,YIDi) .否则,C查询LH1列表(IDi,QIDi,μIDi) 和Lp1列表(IDi,YIDi,xIDi) .最后,C返回PKIDi =(QIDi,YIDi) 给A2 ,并将(IDi,QIDi,YIDi) 加入Lp3.
陷门查询:当收到A2 关于IDi的陷门查询时,若IDi =IDI,C终止算法(这个过程由E1表示).否则,C随机选择r2∈Zq*并计算T2=r2P.然后,C查询LH3列表(w,θ,k) 和LH2列表(SKIDj1·PKIDi1,PKIDj,PKIDi,θ) ,计算K2=H3(k',θ2) 、T2=(K2+r2) SKIDi2-1(PKIDi2+αIDiPpub) 和T3=r1(YIDS +QIDS +μIDSPpub).最后,C返回Tw'=(T1,T2,T3) 给A2 .
挑战:A2 给出身份为ID*的挑战关键字w0和w1.若ID*≠IDI,C终止算法(这个过程由E2表示).否则,C首先选择随机值r1∈Zq*并计算C1=r1P.然后,C查询LH3列表(wi,θi,ki) 和LH2列表(SKIDj1·PKIDi1,PKIDj,PKIDi,θ) ,计算K1=H3(ki,θi)、C2=C1+K1·SKIDO2-1(PKIDO2+μIDOPpub) 和C3=r2(YIDS +QIDS +μIDSPpub) .最后,C返回C =(C1,C2,C3) 给A2 .
更多查询:A2 可继续执行以上阶段除挑战关键字w0和w1之外(这个过程由E3表示)的自适应查询.
猜测:A2 给出猜测结果b′∈{0,1} .C设置QIDi =aP,C1=bP.如果(C2-T2+T1)(xIDS +dIDS)-b(YIDS+μIDSPpub)=abP成立,则说明C可以解决CDH 问题.
我们知道只有当E1,E2,E3事件之一发生时,游戏才会中止.下面我们将对C解决CDH 问题的优势ε′进行分析.首先:
接下来,我们将证明:Pr[┐E3] ≥2ε.由于
和
4 性能分析
在本节中,我们将所提出的SCF-PAEKS 方案分别与无安全通道的方案[9] ,[10]和[11]在安全性,计算成本和通信成本方面进行比较.
4.1 安全性能
在表2 中,分别给出了四种方案安全性能的比较.我们分别使用CL、AU、OK、IK 和BP 表示无证书、认证、OKGA、IKGA 和无双线性对.从表2 中可以发现方案[9]是基于公钥基础设施的,存在证书管理问题.方案[10]是基于身份的加密体制,存在密钥托管问题.方案[11]没有对数据拥有者身份认证的功能,敌手可以冒充数据拥有者发起OKGA 和IKGA.此外,方案[9],[10]和[11]都依赖于高消耗的双线性对.

表2 安全属性比较Table 2 Comparison of security attributes
4.2 计算成本
在本节中,我们将使用方案[14]中的测试结果来估计四种方案的计算成本.在方案[14]中,性能的评估是在配备有Ubuntu 16.04 操作系统的电脑上进行的,使用MIRACL 库,配备了I5 -4210U 1.7 GHz 处理器和4 G字节内存.这里Thm,Tsa,Tb,Tsp,Th分别表示哈希映射到点的执行时间4.362 ms,标量加法的执行时间0.013 ms,双线性对的执行时间4.154 ms,标量乘法的执行时间1.631 ms,一般哈希函数的执行时间0.004 ms.
如表3 和图2 所示,我们分别从密钥算法、加密算法、陷门算法和测试算法给出了这四3 个方案的计算成本.实验结果表明,在密钥算法中,所提出的SCF-PAEKS 方案的计算成本比方案[9],[10]和[11]分别降低了33.42%,61.73%和18.25%.在加密算法中,所提出的SCF -PAEKS 方案的计算成本比方案[9],[10]和[11]分别降低了22.88%,55.33%和75.33%.在陷门算法中,所提出的SCF -PAEKS 方案的计算成本比方案[9],[10]和[11]分别降低了24.1%,39.32%和64.86%.在测试算法中,所提出的SCF-PAEKS 方案的计算成本比方案[9]高出17.97%,与[10]和[11]相比分别降低了64.86%和77.2%. 可见所提出的SCF -PAEKS 方案的计算成本在各算法中基本均为最低.这是因为我们的方案使用了标量乘法而不是高消耗的双线性对.因此,与其他方案相比,我们的方案具有更高的效率.

表3 计算成本比较(ms)Table 3 The comparison of computation cost (ms)
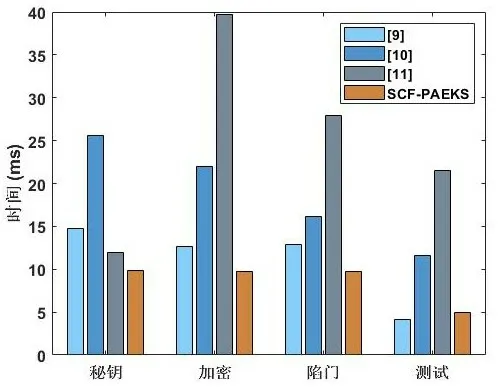
图2 计算成本比较Fig 2 The comparison of computation cost
4.3 通信成本
下面,我们将分别从公钥、加密、陷门的大小(分别用PK、 EN 和TD 表示)来比较四种方案的通信成本.另外,我们假设点G、G1、G2和Zq*的大小分别为320 位、512 位、1 024 位、和160 位.表4 和图3 显示,所提出的SCF-PAEKS 方案中PK 的通信成本比[9],[10]和[11]均高出25%.所提出的SCF-PAEKS 方案中EN 的通信成本与方案[9],[10]和[11]相比分别降低了19%、53%和19%.此外,所提出的SCF -PAEKS 方案中TD的通信成本比方案[9]和[10]略低,但与方案[11]相比降低了38%.

表4 通信成本比较Table 4 The comparison of communication cost
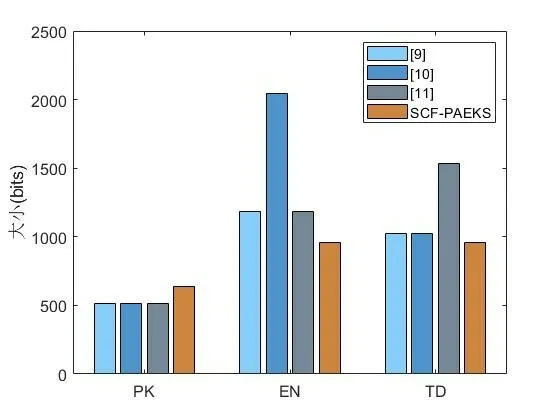
图3 通信成本比较Fig 3 The comparison of communication cost
由上述结果表明,所提出的SCF-PAEKS 方案中公钥的通信成本相对其他方案略高.但方案[9]存在证书管理问题,方案[10]是基于身份的加密,无法避免密钥托管问题.方案[11]容易受到关键字猜测攻击.特别地,上述三个方案均不可避免双线性对,导致其计算和通信成本都较高.因此,本文推出的方案更安全、更高效.
5 结论
云服务的出现给数据隐私带来了一些挑战.为了确保数据安全和对加密数据的高效搜索,一些SCF-PEKS方案被提出.然而,这些方案均存在一定的不足.在本文中,我们提出了一个无双线性对的SCF -PAEKS 方案.它不仅解决了加密数据的安全存储和检索问题,而且不存在证书管理和密钥托管问题.新颖的是,该方案不依赖于高消耗的双线性对且可有效抵抗IKGA.分析结果表明,SCF-PAEKS 具有较好的综合性能.
