基于数字滤波的低频时码秒脉冲抖动平滑方法研究

齐 震,程浪浪,刘 强,王 昕,赵 凡,高玉平,冯 平

(1. 中国科学院国家授时中心,西安 710600; 2. 封开低频时码授时台,广东 肇庆 526500; 3. 中国科学院大学,北京 100049)

0 引言

低频时码授时技术属于长波授时技术的一种扩展,是国际电信联盟(International Telecommunication Union, ITU)一直提倡的一种授时技术[1]。目前,已有多国建有低频时码授时系统,如中国BPC、美国WWVB及日本JJY等[2]。低频时码授时的优势在于借助低频载波通过天波和地波进行时间信号传输,具有较高的相位稳定性,传播损耗小,可以远距离传输[1]。我国于2007年建成的商丘低频时码授时台,采用幅度调制体制,调制速率为1 bit/s,通过4种不同脉宽传递时间信息,在每秒开始时刻使幅度下跌90%标志UTC(NTSC)秒的起始时刻[3-4]。其中,低频时码授时系统的系统时间与UTC(NTSC)的时间同步通过卫星共视实现。

随着数字电子技术的不断发展,低频时码接收机也朝着数字化、小型化的趋势发展,所采用的定时手段也趋向数字化解决方案[5]。低频时码授时信号从发播台至用户接收终端的过程中,会受到各种环境的干扰以及信号传播链路时延的影响,因此接收端往往接收到的低频时码秒脉冲会存在随机抖动现象,在一定程度上影响定时精度[6]。为提高定时精度,需对秒脉冲的抖动进行平滑。本文将利用接收到的我国商丘低频时码发播台发播的BPC授时信号,分别对最小均方误差(least mean square, LMS)自适应滤波和卡尔曼滤波这两种数字滤波方法在低频时码秒脉冲抖动平滑处理中的平滑性能进行仿真验证分析。

1 原理及方法

1.1 低频时码秒脉冲抖动平滑方法

BPC授时信号到达接收终端后通过解调得到的1PPS与国家授时中心标准时间UTC(NTSC) 1PPS之间存在一个由于传播路径及设备时延等因素产生的固定相位差,该相位差可通过理论模型计算和接收终端设备标定获得。同时,接收终端的内部工作时钟源产生的本地1PPS与BPC 1PPS之间存在一个随机的相位差,该相位差是由于设备上电瞬间本地1PPS初始相位随机产生导致,可通过接收终端内部测量获得,每次断电重启后会发生变化。

而在实际BPC信号接收时,受接收环境干扰等影响,解调得到的BPC 1PPS存在抖动现象。因此BPC 1PPS与UTC(NTSC) 1PPS之间的相位差会对应地出现幅度抖动,同理,BPC 1PPS与本地1PPS之间的相位差会出现同样幅度变化的抖动。

所以,接收终端解调得到的BPC 1PPS的抖动现象可以通过接收终端内部测量BPC 1PPS与本地1PPS的相位差波动情况进行量化反映。对该抖动的相位差进行滤波平滑处理后,结合已标定的时延对本地1PPS进行修正,使其与UTC(NTSC) 1PPS保持同步,接收终端即可输出标准稳定的1PPS。原理如图1所示。

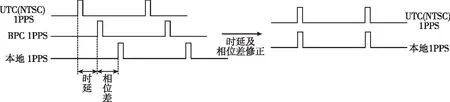
图1 BPC接收终端秒脉冲同步修正原理图Fig.1 BPC receiver 1PPS synchronization correction schematic diagram

BPC接收终端秒信号修正原理如图2所示。天线接收BPC授时信号并解调,然后得到BPC 1PPS(one pulse per second),同时本地高稳晶振提供的工作频率信号经分频倍频得到本地1PPS,再对上述两个1PPS的脉冲边沿进行捕获,利用时钟计数器得到两个脉冲之间的时差值,该时差值即为BPC 1PPS和本地1PPS之间的相位差。对获得的时差值进行数字滤波,将滤波结果作为本地1PPS进行第一次移相修正,然后再附加时延修正,即可输出与UTC(NTSC) 1PPS保持同步的1PPS。

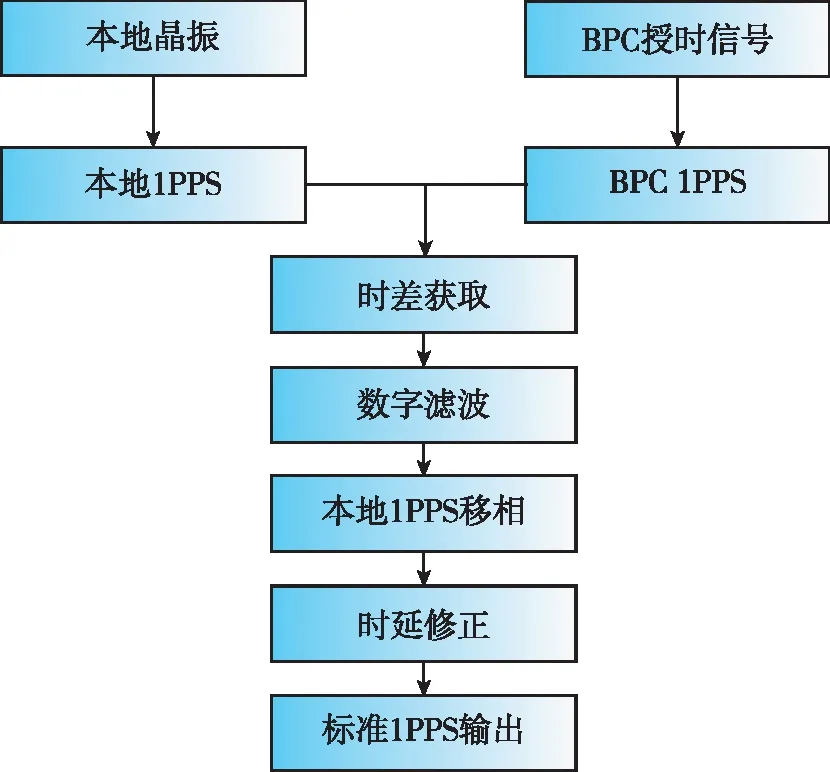
图2 BPC接收终端秒信号修正原理图Fig.2 BPC receiver second signal correction schematic diagram

1.2 数字滤波原理

1.2.1 LMS自适应滤波

本文采用基于最小均方误差(least mean square, LMS)算法的自适应滤波方法,是一种改进的最陡下降算法,不需要对信号提取先验统计,具有计算量小、易于实现的特点[7]。如图3所示自适应滤波器原理,输入信号x(n)经过可调节参数滤波器后得到输出信号y(n),再与期望信号d(n)对比后得到误差信号e(n),然后通过自适应算法对滤波器参数进行调整,最终使e(n)的均方值最小[8]。自适应滤波利用前一时刻已得的滤波器参数的结果,自动调节当前时刻的滤波器参数,以适应信号和噪声随时间变化的统计特性,从而实现最优滤波[9]。

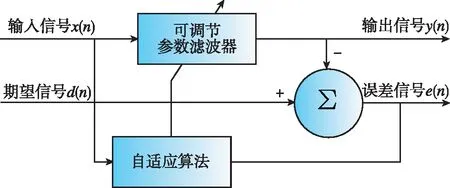
图3 LMS自适应滤波器原理图Fig.3 Principle of LMS adaptive filter

所以,LMS自适应滤波算法主要分为两个部分:滤波和和自适应调整。其算法过程如下[7]

(1)

e(n)=d(n)-y(n)

(2)

w(n+1)=w(n)+μe(n)x(n)

(3)

式中,N为滤波器的阶数;μ为步长因子,取值需要满足公式(4),即0<μ<1/λmax,λmax为输入信号自相关矩阵的最大特征值。

|1-2μλmax|<1

(4)

根据LMS自适应滤波原理,在对秒脉冲进行滤波处理时需设置4个输入信号,分别为时差信号、时差期望信号、步长因子信号和滤波器阶数信号。时差信号为BPC 1PPS和本地1PPS之间的相位差;时差期望信号为一定时间内时差信号的均值,同时利用该时间段内的时差信号计算自相关矩阵的最大特征值,从而确定步长因子;滤波器阶数可根据硬件资源情况确定,一般为8阶,而本文通过仿真进一步分析了不同阶数对滤波性能的影响。

1.2.2 卡尔曼滤波

卡尔曼滤波利用递归算法解决时域离散数据的滤波问题,是基于最小误差准则的最优线性估计[10-11]。卡尔曼滤波可对平稳和非平稳随机信号进行较高精度的估计,由于系统的当前状态只与前一时刻的系统状态以及当前测量值有关,所以无需过去所有的测量值,只需前一时刻的系统状态与当前时刻的测量值就可以对当前状态实现最优估计[12-13]。卡尔曼滤波是通过预测和更新两个阶段实现对系统的最优估计,基本模型如下[14]。

首先构建一个离散线性系统模型,见式(5)、式(6)[15]

xk=A×xk-1+B×uk+ωk-1

(5)

zk=H×xk+vk

(6)

其中,xk为k时刻系统的状态矩阵;xk-1为k-1时刻系统的状态矩阵;A为状态转移矩阵;B为控制输入矩阵;uk为系统控制输入;ωk-1为过程噪声;zk为k时刻系统的观测量;H为状态观测矩阵;vk为系统噪声。

基于该离散系统模型,假设过程噪声与系统噪声均为高斯白噪声,即P(ω)∈N(0,Q),P(v)∈N(0,R),其中Q和R分别为ω和v的协方差。可得预测方程为[15]

(7)

(8)

更新方程为

(9)

(10)

(11)

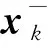
在秒脉冲卡尔曼滤波处理中,由于信号在高斯信道中传输,当前时刻系统的预测值为上一时刻系统的输出值,所以令状态转移矩阵A设为1,控制输入矩阵B设为0,状态观测矩阵H设为1,单位矩阵E设为1。故式(7)～(11)可更新为

(12)

(13)

(14)

(15)

(16)

2 仿真验证分析

本文利用已有的BPC接收设备所采集的BPC 1PPS和本地1PPS时差作为滤波模块的输入信号进行MATLAB仿真分析。该接收设备的本地1PPS由JKOC36A-10 MHz型号的恒温晶振提供,其频率准确度为±0.03×10-6,日老化率为±0.5×10-9。数据选用23点后采集的1 h数据,共3 600个采样点。

2.1 LMS自适应滤波仿真结果分析

LMS自适应滤波的仿真结果如图4～图7所示。为研究滤波器不同阶数对滤波结果的影响,本文分别从8阶、16阶、32阶和64阶分析LMS自适应滤波的性能。根据仿真结果发现,LMS自适应滤波算法可以有效平滑秒脉冲的抖动现象,并且随着滤波器阶数的增加,平滑效果越好。对滤波结果一次差分如图8～图11所示,在滤波器阶数为8阶时,相邻采样点之间的波动在1 ms左右,甚至在部分时间段波动超出1 ms。当阶数增加至16阶时,平滑效果稍有改善,随着阶数继续增加,滤波结果的稳定性也明显改善。分别统计8阶、16阶、32阶和64阶LMS自适应滤波器滤波结果标准差以及原始数据标准差如表1所示,原始数据标准差结果为2.894 ms,经LMS自适应滤波处理后,标准差可以提升到0.569 ms。如图12所示的LMS自适应滤波器的阶数同滤波结果标准差之间的变化趋势可以发现,标准差的变化趋势随着阶数变大而慢慢趋于平稳,最终稳定在0.5 ms附近。统计滤波前后均值可以发现,与原始数据均值相差最大的是采用8阶滤波,相差0.201 ms,与原始数据均值相差最小的是采用32阶滤波,相差仅0.002 ms。所以,在实际应用中采用LMS自适应滤波应当选择合适的滤波阶数,以达到较好的滤波效果。虽然随着滤波阶数的增加,会获得更好的滤波效果,但是在电路实现中,多阶数滤波对应消耗更多的电路逻辑资源。综上所述,LMS自适应滤波可以有效地平滑低频时码秒脉冲的抖动,但是在实际应用中应根据滤波性能和资源使用情况合理选择滤波阶数。

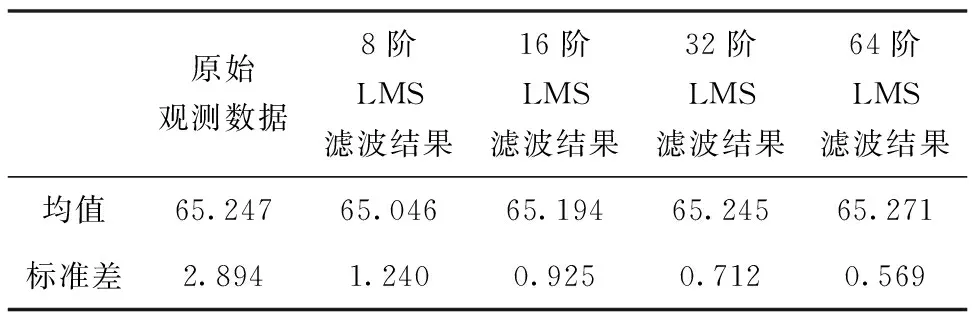
表1 LMS自适应滤波结果的标准差及均值统计Tab.1 Standard deviation and mean statistics of LMS adaptive filtering results ms

图4 8阶LMS自适应滤波仿真结果Fig.4 Simulation results of 8-order LMS adaptive filtering

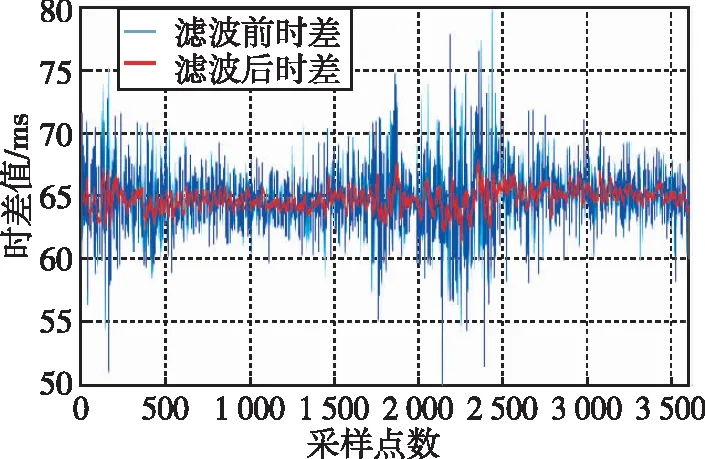
图5 16阶LMS自适应滤波仿真结果Fig.5 Simulation results of 16-order LMS adaptive filtering

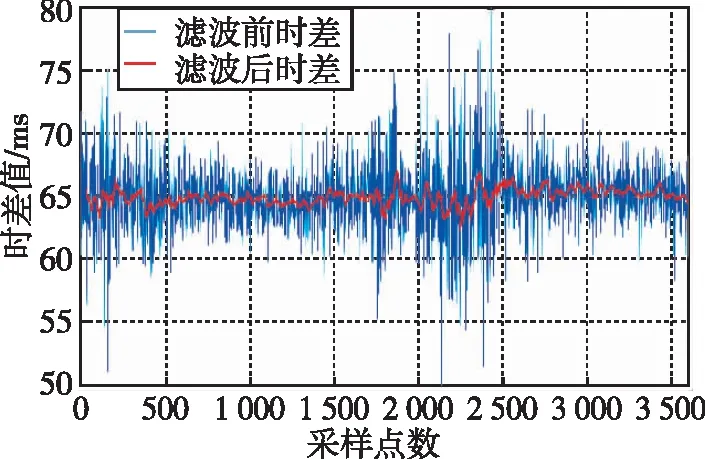
图6 32阶LMS自适应滤波仿真结果Fig.6 Simulation results of 32-order LMS adaptive filtering

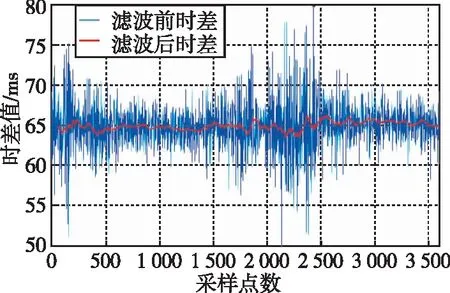
图7 64阶LMS自适应滤波仿真结果Fig.7 Simulation results of 64-order LMS adaptive filtering

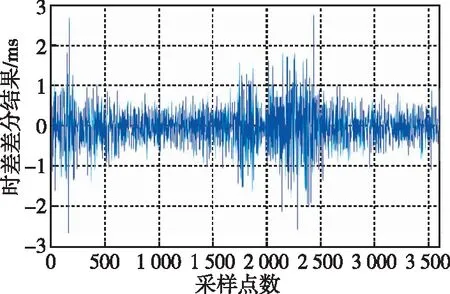
图8 8阶LMS自适应滤波仿真结果一阶差分Fig.8 First-order difference of 8-order LMS adaptive filtering simulation results

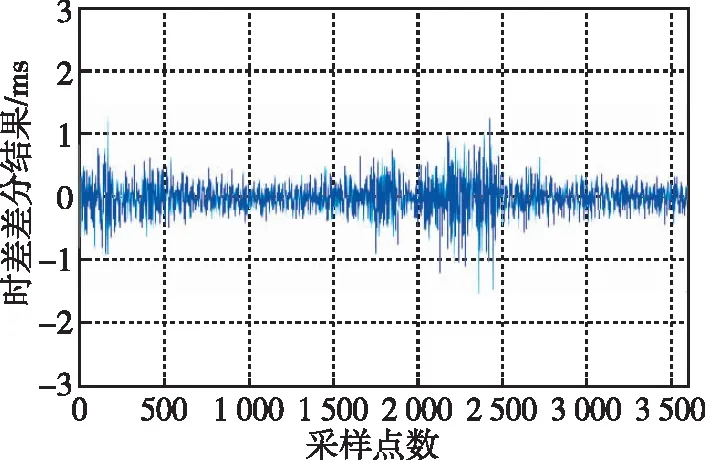
图9 16阶LMS自适应滤波仿真结果一阶差分Fig.9 First-order difference of 16-order LMS adaptive filtering simulation results

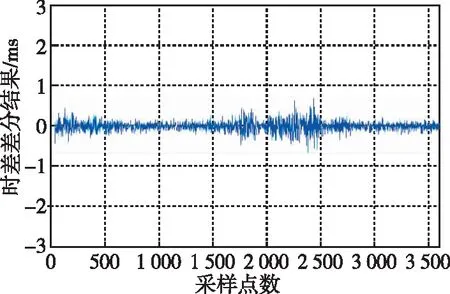
图10 32阶LMS自适应滤波仿真结果一阶差分Fig.10 First-order difference of 32-order LMS adaptive filtering simulation results

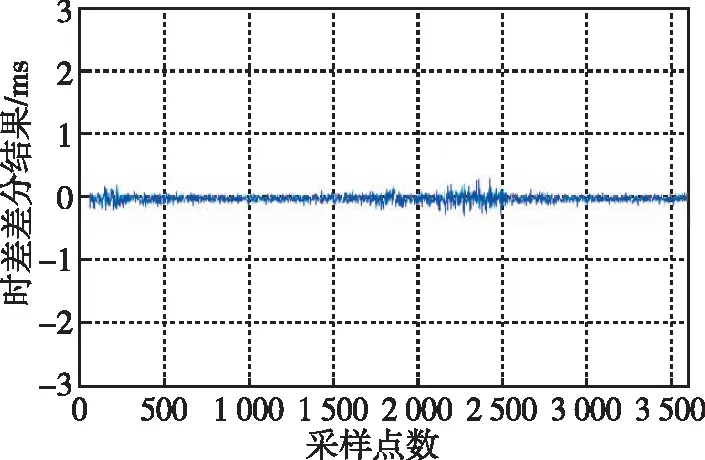
图11 64阶LMS自适应滤波仿真结果一阶差分Fig.11 First-order difference of 32-order LMS adaptive filtering simulation results

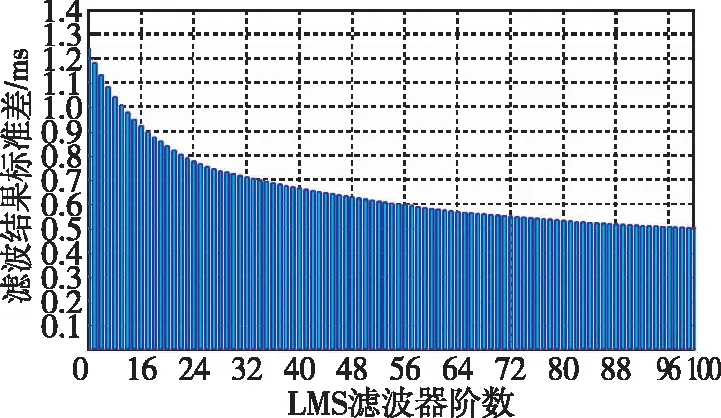
图12 LMS自适应滤波器阶数与滤波结果标准差关系图Fig.12 The relationship between the order of LMS adaptive filter and the standard deviation of filtering results

2.2 卡尔曼滤波仿真结果分析

卡尔曼滤波仿真结果如图13所示,可以发现卡尔曼滤波在平滑秒脉冲抖动应用上具有非常明显的效果。图中红线为滤波结果,收敛后的结果接近于一条直线。卡尔曼滤波结果的一阶差分结果如图14所示,在滤波的初始阶段大约有近700 s的收敛时间,但收敛后的结果表现十分稳定。计算已收敛时间段内的均值和标准差如表2所示,标准差由2.894 ms提升至0.084 ms,均值稍有0.342 ms的偏差。

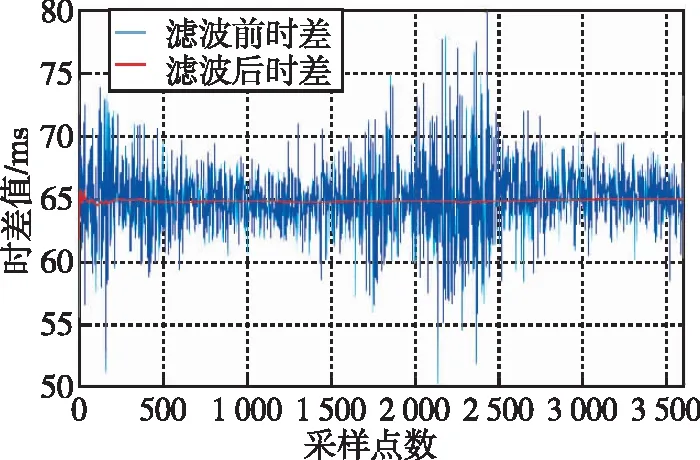
图13 卡尔曼滤波仿真结果Fig.13 Kalman filter simulation results

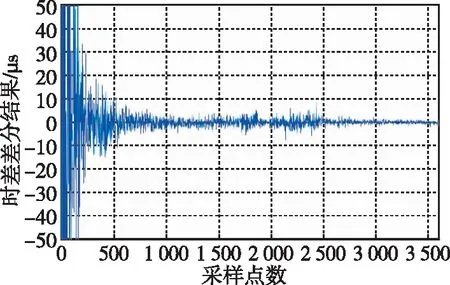
图14 卡尔曼滤波仿真结果一阶差分Fig.14 First-order difference results of Kalman filter simulation

2.3 不同滤波方法对比分析

对比LMS自适应滤波和卡尔曼滤波在秒脉冲平滑处理的结果,发现卡尔曼滤波的效果要优于LMS自适应滤波,但是卡尔曼滤波存在一定时间的收敛过程,所以滤波响应时间上,LMS自适应滤波要优于卡尔曼滤波。如图15所示,利用Allan方差对比两种滤波结果的频率稳定度可以发现,卡尔曼滤波的结果明显优于LMS自适应滤波。所以在实际应用中,可根据需求合理选择滤波策略进行秒脉冲抖动处理,若对定时稳定性及精度要求较高可以选择卡尔曼滤波,若对系统响应时间要求较高,而对定时精度没有过高需求可以选择LMS自适应滤波。

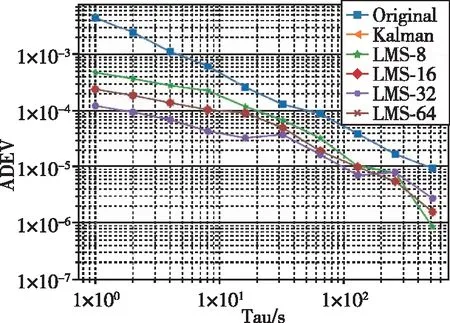
图15 原始数据与不同滤波方法的Allan方差Fig.15 Allan variance of original data and different filtering methods

3 结论

本文通过研究BPC 1PPS抖动平滑原理,并利用BPC接收机实际采集的BPC 1PPS和本地1PPS相位差数据,对LMS自适应滤波和卡尔曼滤波秒脉冲抖动平滑仿真分析,得到以下结论:

1)BPC信号在传播过程中受环境等因素的影响而发生的秒脉冲抖动可以通过BPC 1PPS和本地1PPS的相位差反映,对该相位差抖动平滑后用于校准本地1PPS可以有效提高BPC定时精度和稳定性。

2)卡尔曼滤波和LMS自适应滤波对于低频时码秒脉冲的抖动平滑都具有明显效果,卡尔曼滤波的平滑效果和频率稳定度表现更优,收敛后滤波结果标准差为0.084 μs。LMS自适应滤波随着滤波器阶数的增加,滤波效果也不断改善,最终滤波结果标准差稳定在0.5 ms附近。

3)上述两种滤波方法有各自的优势和缺陷,LMS自适应滤波的滤波结果响应时间快,但滤波性能受阶数的影响,而高阶滤波器在电路实现中会消耗更多资源;卡尔曼滤波具有较好的滤波性能,但需要一定的时间进行收敛。所以,在秒脉冲抖动平滑的实际应用中,应根据实际需求合理选择滤波器。