基于“当前”统计模型的卡尔曼滤波在北斗单向授时中的应用

柯腾伦,孙光辉,吴荣刚,丁凯生,陈睿容

(1.北京遥感设备研究所,北京 100086; 2.西安电子科技大学雷达信号处理全国重点实验室,西安 710071)

0 引言

当今世界时间信号的精度在工程技术、基础研究及日常生活等领域中的作用愈发凸显,对授时精度的要求越来越高[1]。传统授时方法如网络时间协议授时法受存储空间及计算能力等限制,授时范围和授时精度不足[2],而通过全球卫星导航系统(global navigation satellite system, GNSS)进行授时具有低成本、高精度、广域性、开放性和可对移动用户服务等优点,成为了当前最主要的授时工具,并得到了广泛的研究[3]。

GNSS单向授时是指接收机通过观测量自主解算接收机钟差,并利用其对接收机秒信号产生电路进行修正,输出标准时间信号以实现授时的方法[4]。GNSS单向授时又可以分为基于伪距测量的GNSS单向授时和GNSS精密单点定位 (precise point positioning, PPP)授时[5]。

基于伪距测量的GNSS单向授时使用广播星历和广播星钟,授时精度一般在10～20 ns。刘利等[6]对BDS-3提供的各种授时服务进行了比较分析,结果表明RNSS(radio navigation satellite service)授时精度和RDSS(radio determination satellite service)双向授时精度相当,介于SBAS(satellite-based augmentation service)授时精度和RDSS单向授时精度之间,在9ns左右;辛洁等[7]研究了BDS不同服务体制下的授时差异,从时空基准、授时精度检核、设备延时及卫星健康状态等方面,分析了基于已知位置的RNSS单/双频授时等模型之间的差异,结果表明RNSS单/双频授时精度分别可以达到8.56 ns和6.89 ns。张大众等[8]利用iGMAS站数据分析了不同轨道卫星的BDS单星授时精度,结果表明GEO、IGSO、MEO卫星的授时精度分别为27.39、18.37和18.62 ns。

GNSS-PPP授时主要使用载波相位、伪距观测数据以及高精度轨道和星钟差等产品,授时精度相对较高。易卿武等[9]提出一种基于北斗三号B2b信号的精密单点授时方法,根据PPP算法实时估算接收机钟差,结果表明与传统的精密单点授时方法相比, 该方法授时精度更高,并且具有成本低、不依赖地面通信网络和分析中心的优势。马祥泰等[10]针对消电离层PPP模型组合噪声大的问题,采用非组合PPP模型对BDS精密授时精度开展研究,结果表明在静态和实时动态条件下,非组合PPP模型精密授时精度均优于消电离层组合PPP模型。韩金阳等分析了不同机构差分码偏差(differential code bias, DCB)产品对选定的2个测站PPP授时精度的影响,实验结果表明所选的2个测站使用不同机构的DCB产品估计钟差的均方差和时间偏差均优于0.4 ns[11]。刘根友等[12]提出了基于PPP的云平台高精度授时方法,采用PPP技术实时解算授时终端钟差,通过驯服恒温晶振输出亚纳秒精度的1 PPS(pulse per second),实现了长时间高精度的授时能力,精密单点授时精度优于1 ns。

BDS目前已经建成,其授时应用研究已成为重要的发展方向,虽然与PPP授时相比,基于伪距测量的单向授时受星历误差、信号传播延时误差和天线位置误差的影响授时精度相对较低,但是其不需要使用实时的精密卫星轨道和钟差改正数产品,也无需较长的时间等待PPP结果收敛[13],因此对基于伪距测量的BDS单向授时进行研究以提高其授时精度具有重要的实际意义。本文通过基于“当前”统计模型的卡尔曼滤波对经由伪距解算获得的钟差进行降噪处理以达到提高授时精度的效果。

1 基于伪距测量的BDS单向授时原理

在BDS单向授时中用户时钟与系统时间的精确同步以及系统时间与UTC时间的精确同步是实现高精度授时的关键所在[14]。单向授时法通过修正接收机本地时间tu来得到协调世界时tUTC,其计算公式如式(1)

tUTC=tu-δtu-δtUTC

(1)

其中,tUTC表示协调世界时;tu表示接收机本地时间;δtu=tu-tsys表示接收机本地时间相对于系统时间的偏移量,即接收机钟差;δtUTC=tsys-tUTC表示系统时间相对于协调世界时的偏移量;tsys表示系统时间。

δtUTC通过导航电文中的模型参数计算获得。如果用户接收机静止且天线位置已知,接收机只要通过跟踪单颗可见卫星,建立单个观测方程就可以求解出δtu;如果用户接收机位置未知,接收机需要通过跟踪4颗或更多可见卫星,通过最小二乘法求解出δtu。下文讨论的都是用户接收机位置未知情况下的BDS单向授时方法。

虽然单向授时在工程上被广泛应用,但是由伪距求解所得接收机钟差δtu容易受噪声影响变得粗糙、杂乱,所以直接使用它来校正接收机本地时间tu所得系统时间tsys的误差较大,授时精度不高,时钟抖动明显。因此本文拟通过将接收机钟差建模为钟差(接收机时钟与参考时钟的初始相位偏差)、钟速(接收机时钟与参考时钟的频率偏差)和频率漂移(接收机时钟频率的变化率),采用基于“当前”统计模型的卡尔曼滤波对其进行处理以降低噪声引起的抖动,达到提高授时精度的效果。

2 基于“当前”统计模型的卡尔曼滤波方程

晶振频率在老化和温度的影响下基本呈现二次型曲线变化,经典钟差模型的表达式如式(2)[15-16]

(2)

其中,δtu(t)表示钟差;a表示初始相位偏差;b表示频率偏差;c表示线性频率漂移;εx(t)表示钟差中的随机分量。

对式(2)求关于时间t的二阶导数,可以得到频率漂移关于时间的表达式

(3)

其中,εz(t)表示频率漂移中的随机分量。

图1所示为通过本地时钟解算钟速前后历元差分计算获得的频率漂移,说明本地时钟频率漂移在零值附近上下波动,该波动呈现出随机噪声的特性。根据式(3)和图1的结果,接收机时钟的频率漂移可以建模为常数加随机分量的形式。

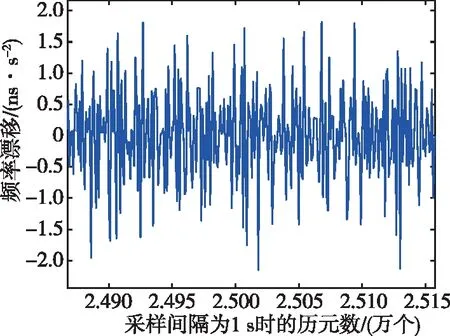
图1 本地时钟解算钟速前后历元差分计算获得的频率漂移Fig.1 The frequency drift calculated by epoch difference of the local clock speed before and after resolution

“当前”统计模型原本是作为一种机动目标跟踪算法在Singer模型的基础上提出的。它将目标加速度建模为加速度均值加零均值有色噪声的形式,因此可以参照“当前”统计模型对于目标加速度的建模,将本地时钟频率漂移建模如式(4)[17]

(4)

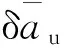
(1)状态方程

将接收机钟差建模为钟差、钟速和频率漂移并对其进行基于“当前”统计模型的卡尔曼滤波,其状态方程如式(5)

(5)

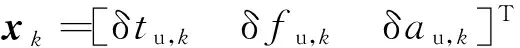
“当前”统计模型中状态转移矩阵A的计算公式如式(6)[17]

(6)

“当前”统计模型中输入关系矩阵U的计算公式如式(7)[17]

(7)

在本模型中,系统输入量为接收机钟差和钟速,系统状态量为接收机钟差,钟速和频率漂移,因此输入关系矩阵B的计算公式如式(8)

(8)

式(6)～(8)中的T表示采样周期;e表示自然常数。

(2)观测方程

基于“当前”统计模型卡尔曼滤波的观测方程如式(9)

yk=Cxk+vk

(9)

3 基于“当前”统计模型卡尔曼滤波的BDS单向授时法

基于“当前”统计模型卡尔曼滤波的BDS单向授时法的主要流程如图2所示。

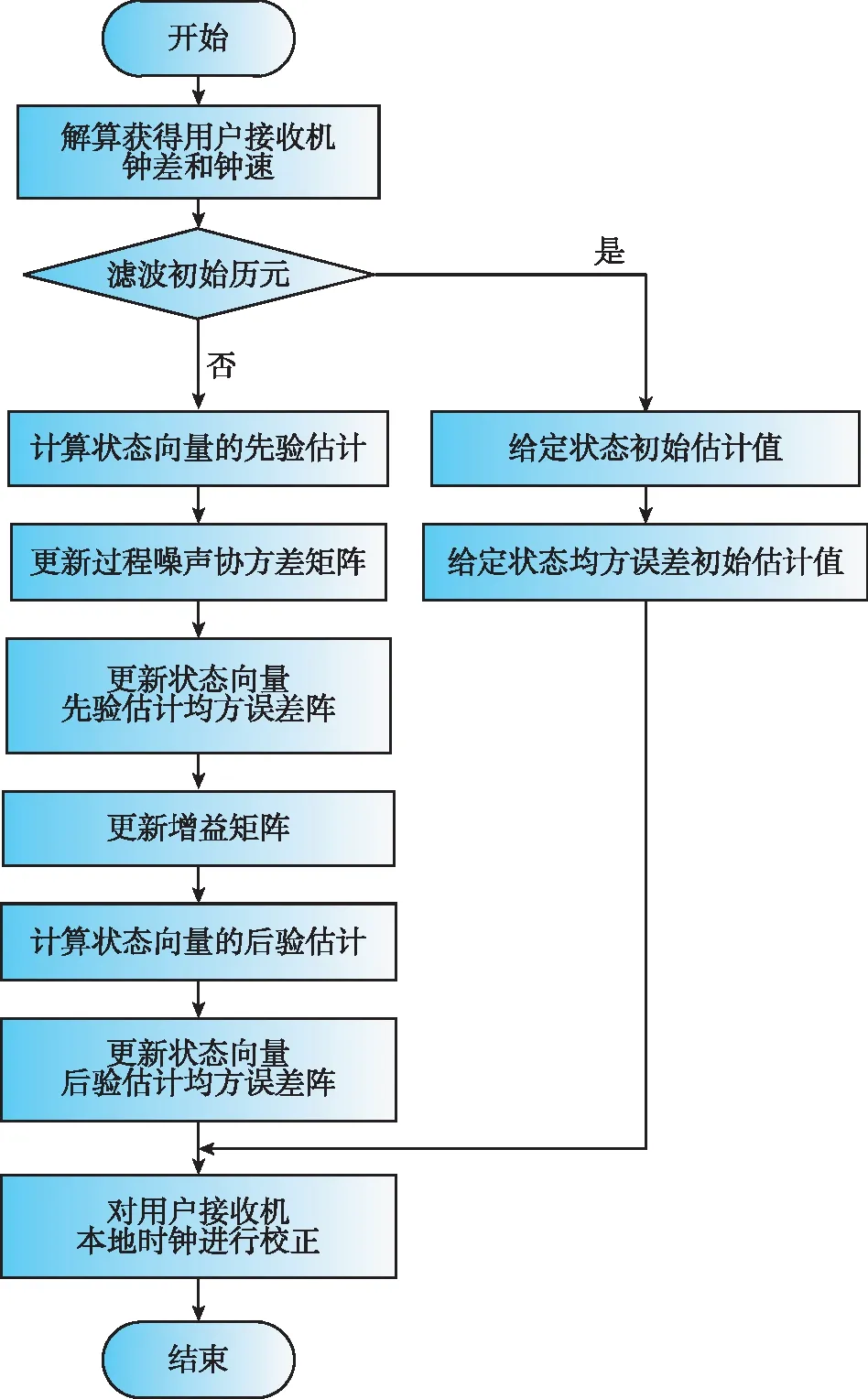
图2 基于“当前”统计模型卡尔曼滤波的BDS单向授时法流程Fig.2 BDS one-way timing service process based on the current statistical model Kalman filter

1)通过伪距、伪距变化率观测方程分别解算获得接收机钟差和钟速。

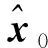
3)利用滤波后的接收机钟差和钟速对本地时钟进行校正。

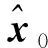
3.1 滤波过程

(1)时间更新过程

状态矢量先验估计值的计算公式如式(10)

(10)

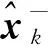
状态矢量先验估计值均方误差阵的计算公式如式(11)

(11)

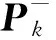
“当前”统计模型中过程噪声矢量协方差矩阵Qk的计算公式如式(12)[17]

(12)

(13)

其中,amax表示给定的最大频率漂移。

(2)测量更新过程

增益矩阵的计算公式如式(14)

(14)

其中,Kk表示增益矩阵;Rk表示测量噪声矢量的协方差矩阵。

测量噪声矢量的协方差矩阵Rk通过采样统计的方法进行计算

(15)

状态矢量后验估计值的计算公式如式(16)

(16)

状态矢量后验估计值的均方误差阵的计算公式如式(17)

(17)

3.2 本地时钟修正

图3所示为接收机本地时钟修正示意图,包含本地时钟修正和伪距变化率修正。

(1)本地时钟修正

首历元仅使用钟差修正相位值,往后使用钟差修正相位值的同时使用钟速修正频率控制字。首次修正后的每个历元都要进行相位修正,其计算方法如式(18)

(18)

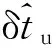
从第2个历元开始,间隔一拍使用钟速修正频率控制字,其计算方法如式(19)

(19)

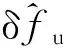
(2)伪距变化率的修正

由于在进行积分多普勒计算时包含中频,所以在计算伪距变化率时需要将中频对应的载波相位积分值减去

(20)

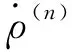
上文对本地时钟的修正只改变观测量的锁存时间,但是作为载波环和码环频率基准的板上晶振或外部时钟并没有被改变,所以需要使用钟速对伪距变化率进行额外修正

(21)

此外对本地时钟的相位修正会使得积分时长改变,导致载波相位积分值发生变化从而影响伪距变化率,对此同样需要加以修正,修正方式如式(22)

(22)

4 实验结果与授时性能分析

为了更直观清晰地体现基于“当前”统计模型的卡尔曼滤波对于BDS单向授时精度的改善效果,设计了相关实验并进行了数据采集与分析。

“当前”统计模型卡尔曼滤波的效果与机动频率和最大频率漂移的取值有关,所以需要研究不同机动频率和最大频率漂移下的授时精度。为了方便对实验结果进行统计分析并排除时间因素的影响,所以选择2022年9月10日至30日每天的同一时段(10∶00至11∶00)采集1小时的数据。天线架设于北京的某大楼楼顶,由于自行研制的导航接收机只能接收北斗B1I频点,所以实验结论都是基于北斗B1I信号。

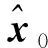
(23)

为了研究算法对于不同类型接收机参考晶振的适用性,实验中分别采用温补晶振(TCXO)和恒温晶振(OCXO)作为接收机的时钟源采集了相关的实验数据,实验组成结构图如图4所示。

图4 实验组成结构图Fig.4 Experimental composition structure diagram

表1和表2分别表示温补晶振和恒温晶振所对应的15组使用经滤波处理后的钟差和钟速对本地时钟进行修正得到的钟差最大波动范围的统计结果,图5和图6是其对应曲线。

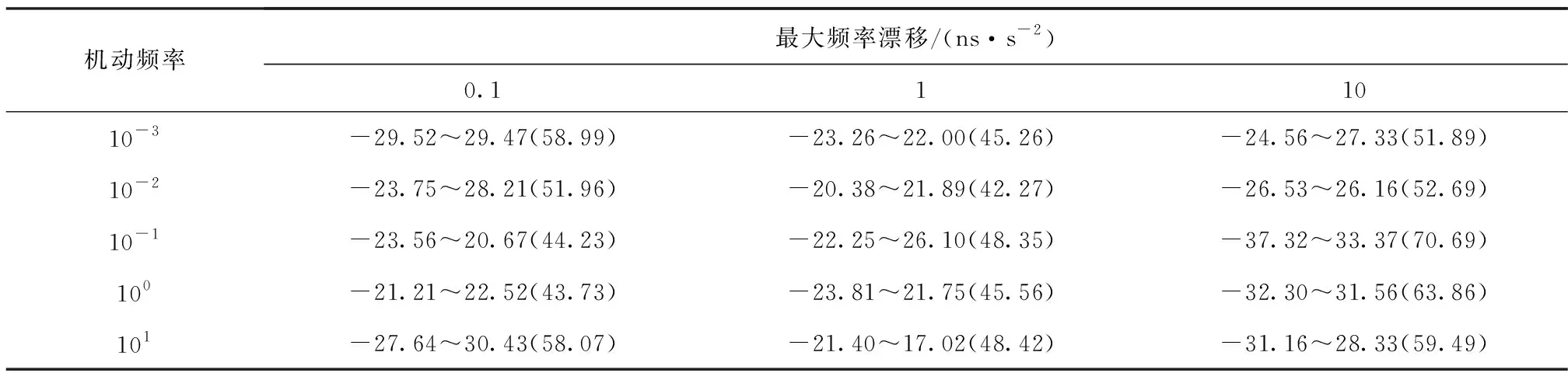
表1 本地时钟钟差最大波动范围统计结果(温补晶振)Tab.1 Statistical results of maximum fluctuation range of local clock error(TCXO) ns

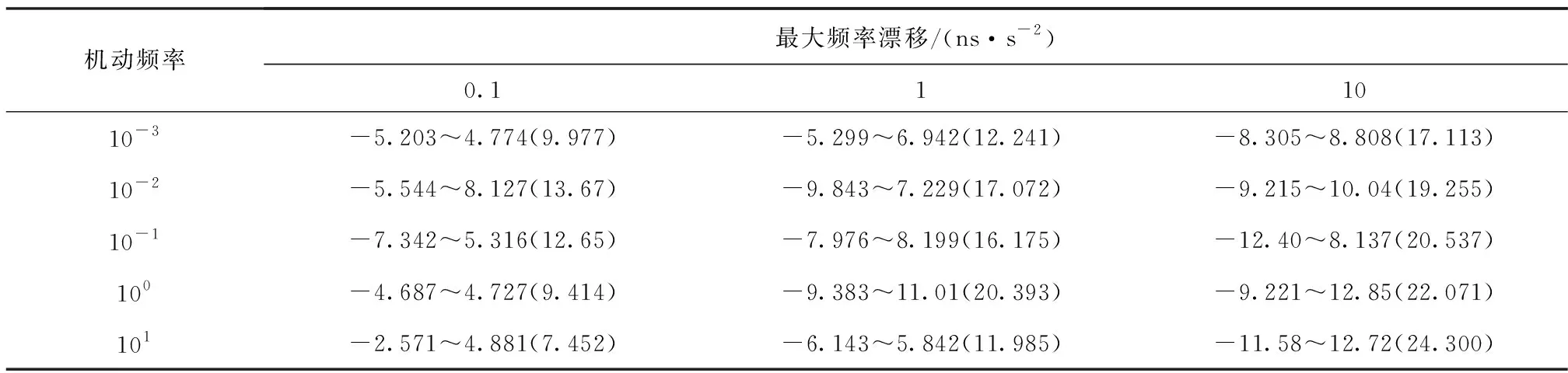
表2 本地时钟钟差最大波动范围统计结果(恒温晶振)Tab.2 Statistical results of maximum fluctuation range of local clock error(OCXO) ns

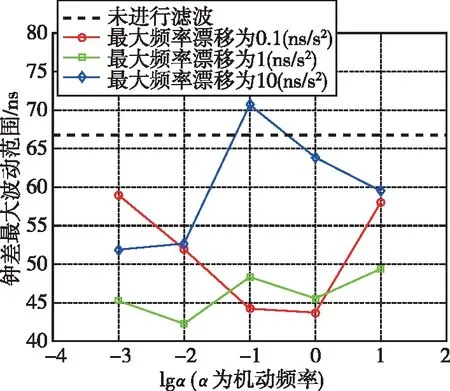
图5 不同机动频率和最大频率漂移对应的本地时钟钟差最大波动范围(温补晶振)Fig.5 Maximum fluctuation range of local clock error corresponding to different maneuvering frequencies and maximum frequency drift(TCXO)

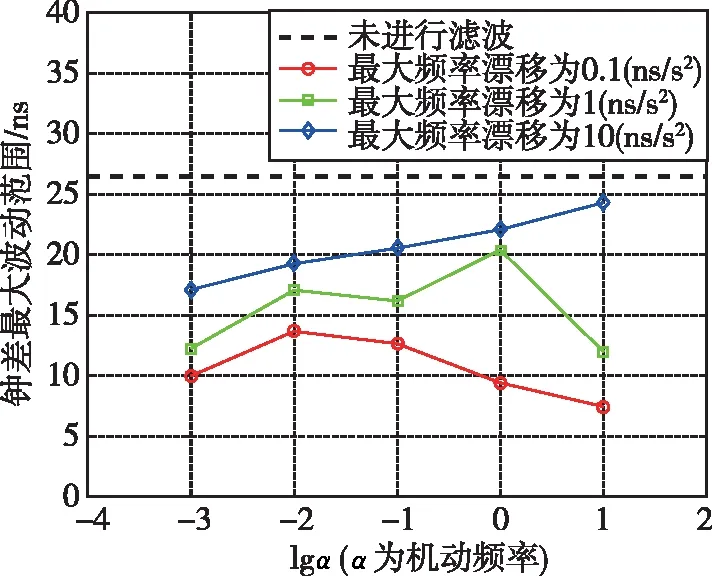
图6 不同机动频率和最大频率漂移对应的本地时钟钟差最大波动范围(恒温晶振)Fig.6 Maximum fluctuation range of local clock error corresponding to different maneuvering frequencies and maximum frequency drift(OCXO)

对于温补晶振,使用未经滤波的解算钟差和钟速直接对本地时钟进行修正得到的钟差最大波动范围为-31.23～35.56 ns,峰峰值为66.79 ns。滤波修正后所得钟差的峰峰值与机动频率和最大频率漂移的取值有关。当最大频率漂移为1 ns/s2且机动频率为10-2时最小为42.27 ns,上下界分别为21.89 ns和-20.38 ns,相比于未滤波修正情况减小了36.7%;当最大频率漂移为10 ns/s2且机动频率为10-1时最大为70.69 ns,上下界分别为33.37 ns和-37.32 ns,相比于未滤波修正情况增加了5.8%。对于恒温晶振,使用未经滤波的解算钟差和钟速直接对本地时钟进行修正得到的钟差最大波动范围为-10.23～16.20 ns,峰峰值为26.43 ns。滤波修正后所得钟差的峰峰值与机动频率和最大频率漂移的取值有关。当最大频率漂移为0.1 ns/s2且机动频率为101时最小为7.452 ns,上下界分别为4.881 ns和-2.571 ns,相比于未滤波修正情况减小了71.8%;当最大频率漂移为10 ns/s2且机动频率为101时最大为24.300 ns,上下界分别为12.72 ns和-11.58 ns,相比于未滤波修正情况减小了8.0%。

表3和表4分别表示温补晶振和恒温晶振所对应的15组使用经滤波处理后的钟差和钟速对本地时钟进行修正得到的钟差标准差的统计结果,图7和图8是其对应曲线。

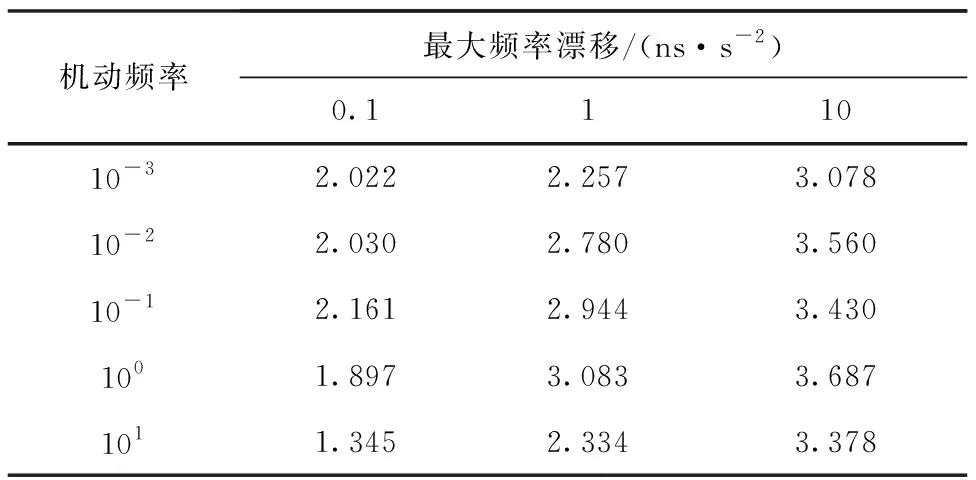
表4 本地时钟钟差标准差统计结果(恒温晶振)Tab.4 Statistical results of standard deviation of local clock error(OCXO) ns

图7 不同机动频率和最大频率漂移对应的本地时钟钟差标准差(温补晶振)Fig.7 Standard deviation of local clock error corresponding to different maneuvering frequencies and maximum frequency drift(TCXO)

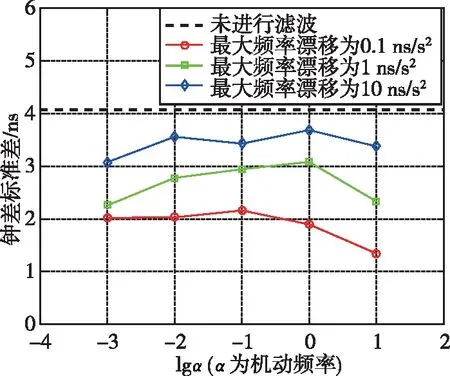
图8 不同机动频率和最大频率漂移对应的本地时钟钟差标准差(恒温晶振)Fig.8 Standard deviation of local clock error corresponding to different maneuvering frequencies and maximum frequency drift(OCXO)

对于温补晶振,使用未经滤波的解算钟差和钟速直接对本地时钟进行修正得到的钟差标准差为9.552 ns。滤波修正后所得钟差的标准差同样与机动频率和最大频率漂移的取值有关。当最大频率漂移为1 ns/s2且机动频率为101时最小为5.489 ns,相比于未滤波修正情况减小了42.5%;当最大频率漂移为10 ns/s2且机动频率为10-1时最大为9.287 ns,相比于未滤波修正情况减小了2.8%。对于恒温晶振,使用未经滤波的解算钟差和钟速直接对本地时钟进行修正得到的钟差标准差为4.075 ns。滤波修正后所得钟差的标准差同样与机动频率和最大频率漂移的取值有关。当最大频率漂移为0.1 ns/s2且机动频率为101时最小为1.345 ns,相比于未滤波修正情况减小了67.0%;当最大频率漂移为10 ns/s2且机动频率为100时最大为3.687 ns,相比于未滤波修正情况减小了9.5%。

由以上分析可知,相比于未滤波修正,在选取合适的机动频率和最大频率漂移的情况下,滤波修正得到的本地时钟钟差的峰峰值以及标准差都能够得到明显的改善。实验结果表明,对于温补晶振,本地时钟钟差的峰峰值最多可以减小36.7%,而标准差最多可以减小42.5%;对于恒温晶振,本地时钟钟差的峰峰值最多可以减小71.8%,而标准差最多可以减小67.0%。另外,对于分别以温补晶振和恒温晶振作为时钟源的接收机时钟,在算法达到最佳改善效果时,对应的最大频率漂移和机动频率的取值是不同的。由此可见滤波修正授时方案的授时性能相较于未滤波修正授时方案的授时性能有明显的提高,基于“当前”统计模型的卡尔曼滤波对于BDS单向授时精度的改善效果十分明显。

以上结论是在使用温补晶振和恒温晶振作为接收机时钟源、接收北斗B1I信号的条件下得出的。理论上本文所提出的方法不限定接收机、晶振与导航信号频点,适用于所有单向授时方法,但是其他条件下对应滤波算法的参数选取会有一定差异,算法的改善效果有待通过后续实验进行验证。

5 结论

本文针对由伪距误差与噪声引起的接收机解算钟差不够平滑、准确导致用户接收机本地时间校准所得系统时间的误差较大、授时精度不高的问题,提出了一种基于“当前”统计模型的卡尔曼滤波单向授时方法。对解算获得的钟差和钟速进行滤波并将滤波结果修正到本地时钟以提高授时精度。使用以温补晶振和恒温晶振作为时钟源的接收机进行实验,结果表明:

1)相比于未滤波修正,在选取合适的机动频率和最大频率漂移的情况下,温补晶振时钟的峰峰值最多可以减小36.7%,标准差最多可以减小42.5%;恒温晶振时钟的峰峰值最多可以减小71.8%,标准差最多可以减小67.0%。

2)对于以不同晶振作为时钟源的接收机,算法达到最佳改善效果时对应的最大频率漂移和机动频率的取值有所不同。

本文提出的方法实现简单,成本低廉,只需要在接收机终端添加相应算法,就能够提升基于伪距测量的GNSS单向授时的授时精度,具有工程实用价值。