集群编队条件下通导一体高精度时间同步方法
2023-07-08吴学颖张吉先胡文涛
吴学颖,张 迪,张吉先,胡文涛,何 伟
(1. 北京自动化控制设备研究所, 北京 100074; 2. 空装驻北京地区第二军事代表室, 北京 100074)
0 引言
集群编队在执行集合探测、预警、指挥及攻击等任务时,相对位置精度和时间精度越高,越能扩大对环境的感知,越有利于保持准确的队形和扩充编队容量,实现任务协同分配、协同搜索及侦察与攻击等[1-2]。集群作战被视为未来极具潜力的新型作战模式[3-4],能够对各类战场设施实现精准协同、集成运用和动态重组[5],作战时间精度每提高一个数量级,其武器效能也会提高一个数量级[6-7]。并且,具有能量积累优势、空间分布式优势、资源灵活调度优势和火力快速分配优势的协同探测成为未来化作战的必然趋势,可以直接决定指挥控制和火力拦截作战效能,已经成为夺取制空权的前提和关键[8-9]。例如,典型的分布式雷达协同探测,为了实现波形的相参处理,要求各分布式雷达间的时间、空间同步精度优于半个波长[9]。所以说,高精度协同时间同步是导弹协同探测、战场统一态势形成与共享、精确指挥控制、战斗协同的重要前提和基础。
基于卫星导航的定位与授时是实现集群编队精确时间同步的一种重要手段[10],美国早在20世纪80年代就已完成GPS部署[11],提出了利用GPS秒脉冲来驯服频率源[12-13]。中国在2000年开始建设属于自己的“北斗”卫星同步导航定位系统[14]。在复杂战场环境下依靠卫星导航系统单点定位可达到米级以上的定位精度,几十纳秒的时间精度,具有全天时、全天候和低成本的优势。目前基于GPS可实现单点定位模式下的20 ns的时间同步精度,基于北斗三代可实现单点定位模式下的10 ns时间同步精度。但是,卫星导航系统在复杂电磁环境下存在被干扰的风险,难以提供可靠的时间同步信息。从20世纪50年代末开始,美军开始研制数据链,大多数战术数据链采用往返计时报文的方法实现平台间时间同步[6]。现有的数据链系统由于信号较强且采用的跳频+扩频以及信道编码等多种手段可以提高其抗干扰、抗摧毁能力,形成基于信息共享的体系对抗优势[3],在复杂电磁环境下的适应性更好,可实现相对测量与定位,满足协同作战需求。例如,Link-16数据链集通信、相对导航和网内识别三大功能于一体,更加适合联合系统作战[15-17],可实现10 ns的时间同步精度。但是数据链系统不能提供绝对的时空基准,其绝对时空基准需要依赖外部输入[18],而且相对定位精度受限。所以说,对于分布式雷达协同探测的半个波长的时间同步需求,只依赖卫星导航系统或只依赖数据链系统均无法实现,需要将卫星导航系统与数据链系统相结合来提高时间同步精度。
1 基于卫星导航载波相位差分的高精度时间同步算法
由于GNSS观测量中的公共误差项具有邻域相似性,即在20 km的邻近区域内的接收机的共视卫星导航观测量中的卫星轨道误差、星历误差、电离层延迟误差和对流层延迟误差等具有高度一致性,因此可以通过与基准节点做载波相位观测量单差组合将其近似完全消除,观测方程中仅保留节点间钟差、整周模糊度和接收机内部噪声分量,通过做双差组合可以进一步将节点间钟差消除[19],进而实现高精度相对定位和时间同步。
传统载波相位差分定位算法建立在基准站固定(即基准站精确位置已知)的基础上,移动站在通过数据链获得基准站的差分信息后,进行差分定位。但是,该定位模式受限于基准站位置固定、通信覆盖范围有限等问题[2],使其在集群编队、空中加油等特殊场合中难以适用。在集群编队完成协同探测或协同作战等任务时,更看重的是各个移动站之间的相对位置与相对时间同步精度,并非绝对位置与绝对时间。因此,针对集群编队应用场景,提出动基座条件下的卫星导航载波相位差分算法来实现高精度相对定位和时间同步,其算法流程如图1所示。
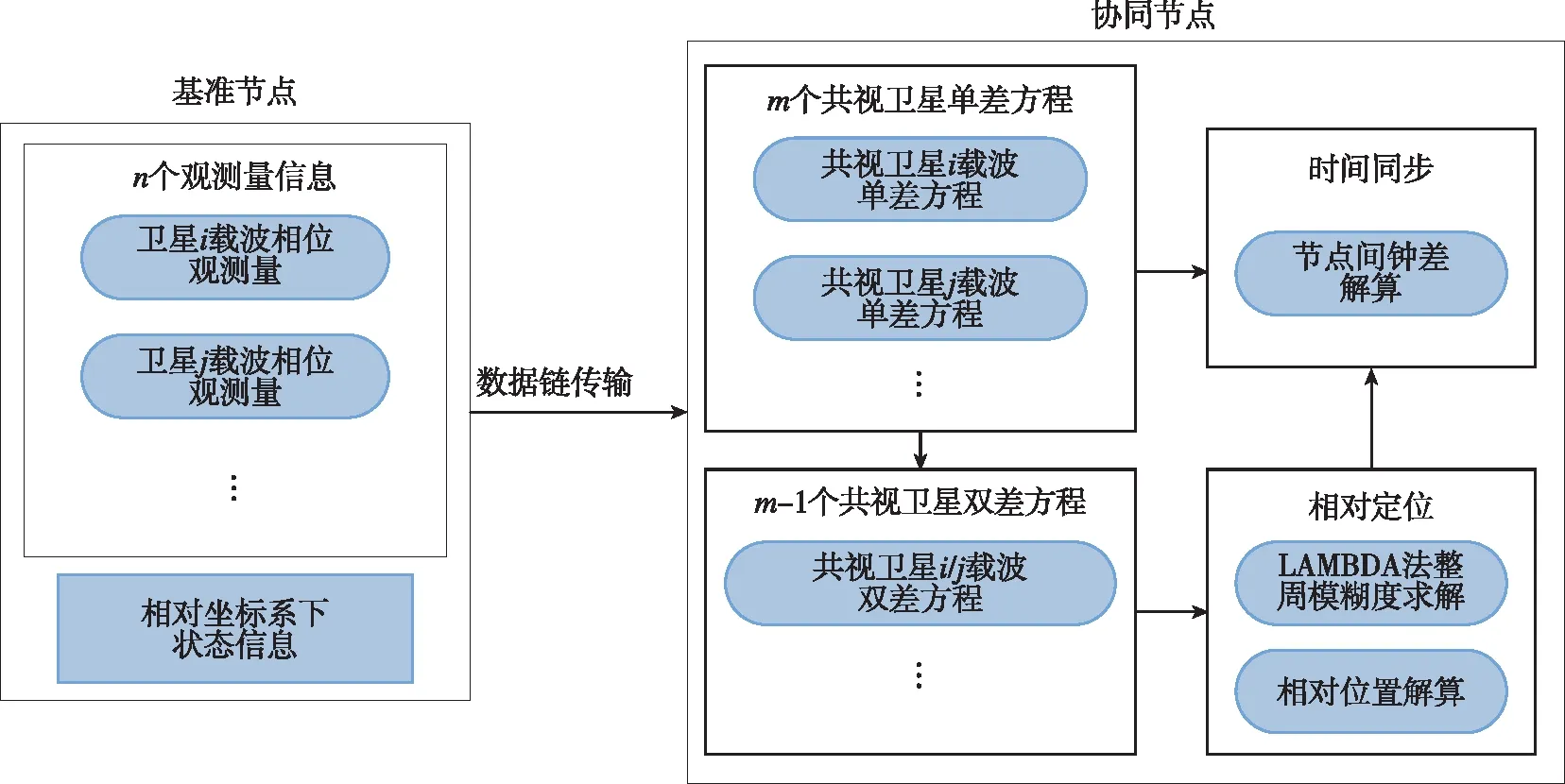
图1 卫星导航载波相位差分定位算法流程图Fig.1 Flow chart of carrier phase difference method for satellite navigation
如图2所示,对于共视卫星i,数据链平台A与B的载波相位观测方程分别为

图2 载波相位差分示意图Fig.2 Schematic diagram of carrier phase difference
(1)

构造载波相位单差组合观测方程,得到
(2)
式中,Δ为单差标记。
单差载波相位观测方程消除了电离层延时和对流层延时,联合对两颗共视卫星i和j的载波相位单差组合观测方程,忽略载波相位测量噪声,可以得到平台A和B的载波相位双差观测方程
(3)

“凡你们的耳,只听金鼓,眼只看旗帜,夜看高招双灯,如某色旗竖起点动,便是某营兵收拾,听候号头行营出战。不许听人口说的言语擅起擅动;若旗帜金鼓不动,就是主将口说要如何,也不许依从;就是天神来口说要如何,也不许依从,只是一味看旗鼓号令。”易平安读完这段,忍不住叹了口气,“戚大帅当年也真够辛苦的,这哪里是带兵,根本是带孩子啊……写得这么简明直白,就算蠢到骆剑峰他们那种程度,也该能够过关了吧?”
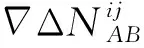
由于载波相位单差方程中仍保留接收机钟差项,因此将通过星间双差解出高精度相对位置信息之后将其代入到站间单差观测方程中,得到两节点之间的钟差差分值,算法流程图如图3所示。
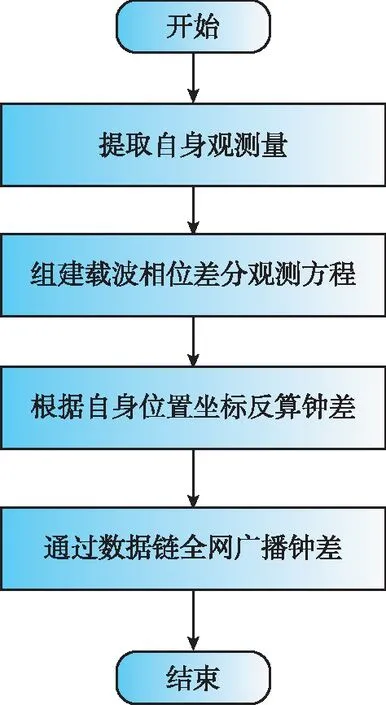
图3 基准节点高精度时间同步算法流程图Fig.3 Flow chart of high precision time synchronization method for reference nodes
(4)

当解算出节点间的钟差后,基准节点通过数据链全网广播其钟差,协同节点收到基准节点广播的钟差后根据与基准节点间的钟差对本地时钟进行修正,算法流程如图4所示,从而实现高精度的时空同步。

图4 协同节点高精度时间同步算法流程图Fig.4 Flow chart of high precision time synchronization method for cooperative nodes
2 基于协同时间驯服的高精度时间同步算法
基于卫星导航载波相位差分的高精度时间同步算法在理论上可实现节点间的高精度时间同步,但在实际应用中由于接收机晶振存在钟漂,会导致两次时间同步之间的时间同步误差发散,如图5所示。以卫星导航载波差分定位解算频率1 s 1次为例,选取某型高性能温补晶振,该型晶振全温状态下的频率准确度为1.8×10-6,短稳峰峰值平均为40.18×10-9,两次时间同步之间,节点间的时间同步误差发散最大为2.55 μs,难以满足组网条件下节点间高精度时间同步的需求。

图5 节点间钟漂不一致导致时间同步误差Fig.5 Time synchronization error from different clock drifts between nodes
如图6所示,基准节点进行修正时由于其单点定位结果存在误差,导致其相对于时间基准的钟差会发生跳变,同时各节点间通过载波相位进行高精度时间同步时难以保证时间误差解算以及修正的同步,最终导致时间修正不同步段时间同步误差存在毛刺的问题,影响节点间的时间同步精度。

图6 相对基准节点时间修正不同步引起的时间同步误差Fig.6 Time synchronization error caused by non-synchronization of relative reference node time correction
针对现有的基于卫星导航载波相位差分的高精度时间同步算法存在的问题,本文提出了基于协同时间驯服的高精度时间同步算法,即通过对协同节点相对于基准节点之间的晶振频漂进行估计的方式来抑制晶振频漂对时间同步精度的影响。协同时间驯服原理如图7所示,令节点0为基准节点,其余N-1个节点为协同节点,基准节点只在上电后进行一次钟差的修正,抑制由基准节点晶振随机游走引起的钟差噪声对时间同步精度的影响;其余时刻由协同节点进行钟差修正,以确保协同节点的钟差与基准节点的钟差漂移方向一致,同时建立晶振误差模型,然后通过让协同节点周期性地利用之前的数据估计出下一测量时间段的晶振误差,最后对其进行补偿修正,修正完成后,消除协同节点与基准节点之间的钟差。

图7 协同时间驯服原理Fig.7 The principle of cooperative time taming
晶振误差输出模型可以表示为[20-21]
(5)
其中,x(T)为晶振相对于起始时刻的相位;x0为初始相位偏差;y0为初始频率偏差;T为两次时间同步之间的间隔;a为频率漂移率;n(T)为晶振的随机误差,由5种独立的随机噪声组成,分别为相位白噪声、相位闪烁噪声、频率白噪声、频率闪烁噪声和频率随机游走噪声。
利用最小二乘法对晶振误差进行预测与估计,即根据测得的相位利用公式(7)拟合出模型的系数,然后对下一时刻的晶振误差进行预测与估计,当接收到新的测量数据时,重新利用新的测量数据进行拟合,更新拟合系数,用更新后的模型再预测下一时刻的晶振误差。然后对其进行补偿修正,消除协同节点与基准节点之间的钟差。
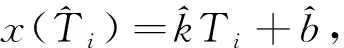
(6)
(7)
3 试验验证
3.1 试验场景
为了对本文提出的集群编队条件下通导一体高精度时间同步算法的有效性进行验证,开展了地面静态试验。试验利用两台通导一体协同接收机进行数据采集,对实际采集到的数据进行处理,测试原理图如图8所示。在本次实验中,数据输出频率为1 k/s,卫星导航载波相位差分算法中定位解算与时间同步周期为1 s。实验中,将两台接收机输出的PPS与本地高稳时钟基准进行对比,得到钟差,并进行记录。
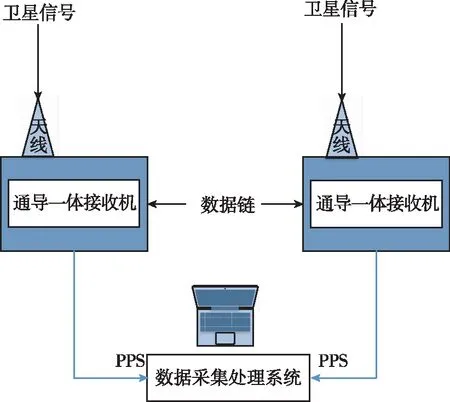
图8 高精度时间同步算法测试原理图Fig.8 Test schematic diagram of high precision time synchronization method
3.2 试验结果分析
在每1 s时刻利用卫星导航载波相位差分算法实现定位解算与时间同步时间同步精度不超过1 ns。当不考虑晶振的随机游走噪声时,由于接收机晶振存在钟漂,因此,钟差随时间累积,由晶振钟漂引起的钟差曲线如图9所示。可以看出,在1 s间隔内,钟差最大可以累积到2 308 ns。因此,每1 s由协同节点按照通过数据链收到的基准节点广播的钟差进行修正,修正后的节点间时间同步误差小于1 ns。
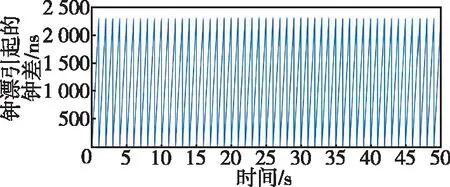
图9 由钟漂引起的钟差曲线Fig.9 Clock error caused by clock drift
在实验中由于环境遮挡与星况变化,接收机的可用星数目如图10所示,PDOP值如图11所示。基准节点在进行时间修正时,其相对于绝对时间系统会存在误差抖动。

图10 可用星数目曲线Fig.10 Curve of available star number
此时现有的基于载波相位差分的节点间时间同步方法由于存在基准节点与协同节点时间修正不同步的问题,会导致节点间时间同步误差存在毛刺如图12所示,最大可达12.02 ns,影响了节点间的时间同步精度。

图12 时间修正不同步引起的时间同步误差曲线Fig.12 Time synchronization error caused by time correction non-synchronization
利用本文提出的基于协同时间驯服的高精度时间同步算法进行节点间高精度时间同步后节点间时间同步误差曲线如图13所示,可以看出,提出的基于协同时间驯服的高精度时间同步算法利用最小二乘法对晶振频率误差进行估计和补偿修正,抑制了晶振频漂对时间同步精度的影响,同时也消除了由于时间修正不同步导致时间同步误差存在的毛刺,保证节点间的时间同步误差小于1 ns,实现了节点间高精度的时间同步。

图13 协同时间驯服后节点间时间同步误差曲线Fig.13 Time synchronization error between nodes after cooperative time taming
4 结论
本文进行了集群编队条件下高精度时间同步技术的研究,通过试验对提出的方法进行了验证,得到以下结论:
1)针对集群编队条件下高精度的时间同步需求,提出了动基座条件下卫星导航载波相位差分算法,使节点间时间同步精度达到1 ns。
2)针对节点间的时间同步误差发散的问题,提出了基于协同时间驯服的高精度时间同步算法,抑制了晶振频漂对时间同步精度的影响,消除了由于时间修正不同步导致时间同步误差存在的毛刺,使节点间时间同步精度从12 ns改善到1 ns。
与传统的利用数据链实现时空同步的方法相比,实现了高精度的时空同步,为未来集群编队作战、高精度协同探测、高精度协同制导等提供高精度的时空基准。
3) 由于卫星导航信号较为微弱,易受干扰,而且在山区、丛林、城市等导航信号受到遮挡的区域,也很难维持高可靠定位服务能力,所以后续需要研究卫星拒止条件下高精度时间同步方法。
