多普勒信息辅助的网络化雷达融合检测

高 畅 谷丰登 严俊坤 贾天一 刘宏伟

(西安电子科技大学雷达信号处理全国重点实验室 西安 710071)

1 引言

雷达的基本用途是利用电磁波对物体或者物理现象进行检测，在国土防御、气象预测以及航空航天等领域发挥着极其重要的作用[1,2]。受限于发射增益、阵列孔径等因素，单雷达站难以满足广域和高精度目标探测的需求，面对日益复杂的电磁环境、高超声速飞行器、隐身飞机等威胁的应对措施有限[3,4]。将多雷达站组网进行协同探测具有空间分集、频域分集、抗毁伤等优势，如何充分利用各雷达站观测信息、提升目标探测性能是近些年的研究热点之一[5–9]。

根据传送数据类型及布站方式的不同，常见的网络化雷达融合检测系统可分为分布式检测系统和集中式检测系统。分布式检测系统通常指各雷达站在对原始接收信息进行局部处理后，将处理结果传送至融合中心进行进一步处理[10]。而集中式检测系统则是将各雷达站接收的原始数据信息传送到融合中心进行融合处理[11]。本文考虑的网络化雷达系统由空间中多个雷达站和融合中心构成，各雷达站将接收到的原始回波数据或局部处理后的回波信息传送至融合中心，融合中心基于这些数据利用特定的融合检测算法给出检测结果，如图1所示[12]。

图1 网络化雷达融合检测系统Fig.1 Networked radar fusion detection system

传统的融合检测算法通常利用各雷达站基于同一共视区域接收回波的幅度信息进行融合处理，并以此来提高检测性能。融合检测技术发展至今，Conte, D’addio等人[13,14]分别研究了基于局部判决结果的融合检测算法。他们推导得到了在不同类型的目标和干扰下，利用“取或”(OR)准则作为融合检测算法准则的最优和次优接收器。Thomopoulos等人[15]研究了基于固定门限的融合检测算法，并进一步将雷达站的检测结果与其对应的数据质量进行了融合。Mathur和Willett[16]着重研究了基于雷达站原始回波数据的融合检测技术，他们研究了高斯白噪声背景下Swerling I 和III目标起伏模型下融合检测性能，并推导了两种目标起伏模型对应最优、次优及求和规则检测器，并研究了局部信噪比对融合检测性能的影响。可以看出，传统的融合检测算法大多仅依据目标回波幅度信息进行判决，而未考虑相干系统中能够获取并使用的多普勒信息。2013年以来，有学者将多普勒信息与空间位置观测的耦合性应用于多帧检测，有效提高了目标与虚警之间的可分性[17–19]，但该方法并未考虑多普勒信息在网络化雷达系统中的应用。

因此，为了充分利用相干雷达系统的多普勒观测信息来提升网络化雷达融合检测性能，本文提出了多普勒信息辅助的融合检测算法。考虑到网络化雷达系统中，不同雷达系统观测到目标的空间位置与径向速度应当满足一定的物理约束，而虚警随机的径向速度较难满足这种约束关系，因此可利用此性质对目标与虚警进行区分[20,21]。换言之，在网络化雷达融合检测过程中利用多普勒信息能够在恒定虚警概率的前提下降低检测门限，进而提升目标检测概率。对雷达站数量不同、雷达布站位置不同以及目标位置不同条件下的仿真实验均表明，本文所提方法与仅基于幅度信息融合检测的传统算法相比，能够有效提升检测性能。

2 传统融合检测算法

假设一网络化雷达系统包含N个雷达站，第i个雷达站观测到回波数据为，其中，Xi表示待检测单元的信号功率，Yi,j表示参考单元的信号功率，n表示参考单元个数。假设影响网络化雷达系统检测性能的因素主要为接收机内噪声，变换到基带后其均为复高斯白噪声。此外，假设影响各雷达站观测的背景噪声分布均匀，各观测值相互独立。不失一般性地，假定目标雷达散射截面积服从Swerling I型起伏模型，在该模型下检测问题可表述为[16]

其中，u(·)表示阶跃函数，ζi表示第i个雷达站接收信号的信噪比，µi表示第i个雷达站所处环境的噪声功率，H0和H1分别表示目标是否存在的假设。

此处假设各雷达站获取的观测相互独立。需要注意的是，由于本文所提空间位置与多普勒信息组成的约束与基于幅度信息的融合检测相互独立地实施，因此本文所提算法也可适用于各雷达站回波具有相关性的场景，在该场景下，将相应基于幅度信息的融合检测算法设计为能够应对各雷达站观测具有相关性的算法即可[22,23]。参考单元平均恒虚警算法，雷达系统接收机内噪声功率µi通过参考单元信号估计得到：

基于此估计值以及检测单元的功率观测值Xi可构造各局部雷达站的检验统计量：

此时式(1)所述的目标检测问题可表述为

根据Neyman-Pearson准则，融合中心的最优融合检验统计量为

当参考窗长n接近无穷大时，式(5)趋近于：

可以看到，次优融合检测器(6)是对检验统计量Zi的加权求和，权重与其信噪比呈正相关。当各雷达站目标的信噪比值ζi≫1,i=1,2,...,N时，基于式(6)可以得到形式更为简洁的融合检测器：

融合检测器相当于将各雷达站的检验统计量进行非相干积累，其优点在于不需要信噪比ζi的先验值，并且当各雷达站观测目标信噪比相同时，该检测器等价于最优融合检测器Topt。

3 多普勒信息辅助的融合检测算法

3.1 算法介绍

传统融合检测算法主要基于各雷达站观测的回波幅度信息，并利用融合检测算法来进行目标检测，而未利用到相干系统中的多普勒信息，即径向速度信息。在实际应用中，目标的运动与其位置、多雷达站观测到同一目标的径向速度之间通常存在一定的耦合性[19]。但是对于本文所关注的虚警而言，由于其源于接收机内噪声，其量测在雷达观测的距离-方位-多普勒数据矩阵中随机分布，因此多雷达站观测的虚警与虚警之间以及虚警与目标之间存在这种耦合性的概率通常较低。本文正是基于这种考虑提出多普勒信息辅助的融合检测算法，对传统仅基于幅度信息的融合检测结果进行二次判断，利用多雷达站观测信息的冗余性提高融合检测性能。

假设在二维空间中存在一个运动目标，速度为vtar=(vx,vy)，相对于第i(i=1,2,...,N)个雷达站的方位角为θTi，径向速度为vTi，则根据速度投影关系得到：

在实际雷达应用场景中，速度和角度的量测都具有一定的误差，并且考虑速度模糊的因素，第i个雷达观测到目标的角度和速度值为

其中，Δθi,Δvi表示角度与速度的量测误差，vDi表示雷达系统的模糊速度，ki表示速度模糊数，m≥0是根据雷达基本参数确定的目标速度最大模糊数。将式(8)中θTi,vTi替换为观测值θOi,vOi，由于误差的存在可能会导致原方程无法成立，此时式(8)左侧式子的值为

由于误差值 Δθi,Δvi通常是微小量，对式(10)最后一个等号右端中括号里面的正余弦函数进行1阶泰勒展开并省略余项可得关于 (vx,vy)的线性形式：

若令量测误差值 Δθi,Δvi是在一定区间上服从一定分布的有界值，即

则对 [vxsin(θOi)-vycos(θOi)]符号进行讨论可得到：

以及

也就是说，若存在qi,ki(i=1,2,...,N)使得不等式组LI存在可行域，则说明多雷达站所观测到速度与角度信息满足上述耦合约束条件，亦即多个雷达站的观测来源于同一目标，据此可判定目标存在；否则说明多雷达站所观测的区域无目标存在。

至此，网络化雷达融合检测问题被转化为判断线性不等式组可行域是否为空集的问题。由于该线性不等式组与线性规划问题中的线性约束条件表示方式一致，因此本文基于单纯形算法求解线性规划问题的思路来对文中线性不等式组可行域是否为空集进行判决。单纯形算法是一类经典的解决线性规划问题的算法，其迭代的初始条件要求线性约束条件可行域非空[24,25]。具体的，本文使用运筹学中快速可靠的两阶段法，利用其第1阶段来对线性规划问题有无可行域进行判决[26–28]。因此将原问题转化为线性不等式组后，即可以利用两阶段算法的第1阶段来对不等式组是否有可行域进行求解。算法1给出完整的算法应用流程。

3.2 算法检测性能理论分析

根据3.1节的分析可知，多普勒信息辅助的融合检测算法在数学上的形式主要是判断线性不等式组有无可行解，若能将多雷达站系统下对应的可行域R在二维坐标图上表示出来，就可以对不同情况下所提算法的检测性能进行评估。根据式(8)，式(13)与式(14)可知，单雷达站对应不等式组式(13)和式(14)中的直线位置关系如图2所示。

图2 单雷达站线性不等式组中直线位置关系Fig.2 Position relation between lines in linear inequalities based on single radar station

其中，L1对应角度与速度的耦合方程(8)，角度量测误差的存在使其斜率发生变化得到L2，速度量测误差的存在使L2的截距发生变化得到L3。L 8 对应进行符号讨论的直线方程vxsin(θOi)-vycos(θOi)=0，L4—L7则对应式(13)与式(14)中其余直线的方程。显然，上述直线满足：L4, L5与L3交于点P1；L6, L7 与L3交于点P2；L5, L7与L8交于点P3；L4, L6与L8交于点P4。并且L3与L8垂直；L4, L5(L6, L7)关于L3对称；L4, L6(L5,L7)关于L8对称。

基于上述结论可知，单雷达站对应线性不等式组的可行域Ri如图3所示。在不存在量测误差情况下，角度与速度耦合方程(8)一定包含在Ri中，也即Ri表示在最大误差容限内所有可能为真值的集合。

图3 单雷达站对应可行域RiFig.3 Corresponding feasible region Ri of single radar station

当多雷达站对应的可行域Ri具 有公共区域时，不等式组式(15)有解，即算法判定该目标非虚警。而本文所提算法的优势主要在于通过抑制虚警来提升检测概率，因此所提算法理论分析的重点在于其抑制虚警的能力，为对该能力进行理论分析，考虑3雷达站系统，且雷达布站位置如图4所示。假设感兴趣目标速度的最大值为vmax＞0，则虚警满足不等式组式(13)—式(15)的概率Pf为3个雷达站对应的可行域在圆内有公共交叠部分的概率。

算法1 多普勒信息辅助的融合检测算法Alg.1 Procedures of the proposed fusion detection method

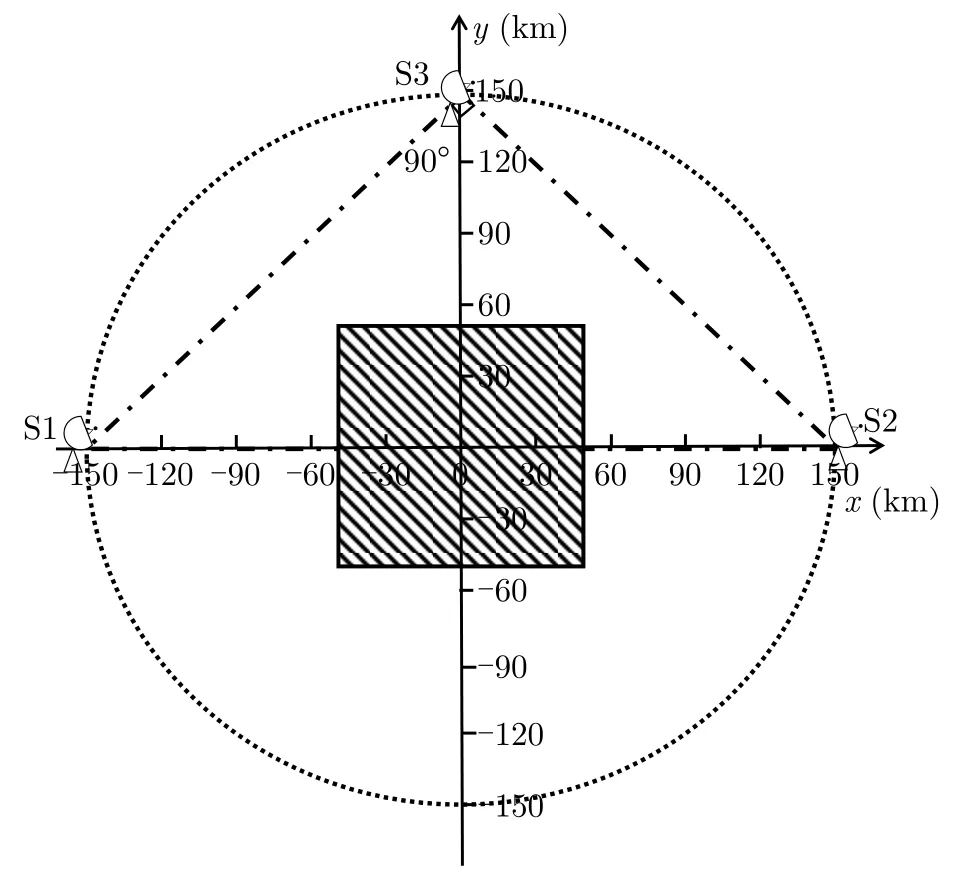
图4 3雷达站系统Fig.4 Three-radar station system

将雷达站S1,S2对应的可行域在圆O中出现交叠记为事件A；S1,S2交叠区域与S3对应的可行域存在交叠记为事件B，则有：

由于算法中物理量之间的非线性耦合关系和不等式组的复杂性，为简化分析给出以下假设条件：

C1: 假设各雷达站观测不存在速度模糊;

C2: 假设当两雷达站对应的L3在圆O中有交点时，即视为两雷达站对应可行域有交叠；

C3: 假设S1,S2对应观测角度之和为180°(或–180°)；

C4: 假设可以忽略角度观测误差，而只考虑速度误差，且各雷达站对应的速度误差限相同，均为Δvmax(＞0)。

上述假设条件中，C1可在高重频雷达体制下成立，C2可在角度和速度误差较小情况下近似成立，C3可在共视区域相对于雷达S1,S2距离较远时近似成立，C4可在高精度雷达测角系统中近似成立。

首先考虑当目标不存在时，雷达站S1和S2对应的可行域R1,R2大致垂直于vx轴，原点到两雷达站对应L3的距离在 [0,vmax]区间内随机分布，两者在圆O中出现交叠的情况如图5所示，图中S1和S2对应的可行域的交叠区域为R。

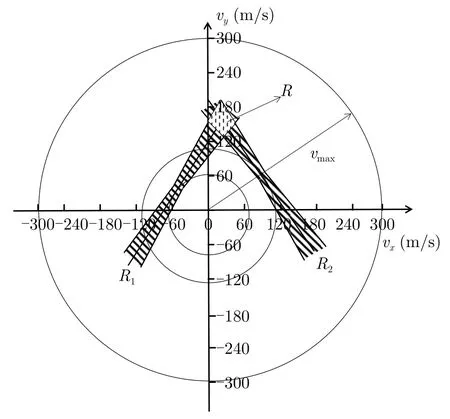
图5 S1,S2对应可行域RFig.5 Feasible region R of S1 and S2

在假设C1—C4下，假设共视区域相对于S1的方向角度范围为 [-θ1max,θ1max]，则当S1观测角度为θ1，观测径向速度为v1时，S1对应的L3位置与存在虚警点的情况下S2对应的L3的可能位置如图6所示，图6阴影区域为存在虚警点时S2对应L3的可能位置，则该区域两边界的距离vc表示存在虚警点时，S2观测的虚警可能径向速度的区间长度。图6中已表明各直线间的位置关系和角度关系，则S1对应的L3与圆O的割线长度为

图6 S1,S2对应L3位置Fig.6 The position of L3 of S1 and S2

则有

则在观测值为 (v1,θ1)下S1,S2对应可行域在圆O中存在交集的概率为

则S1,S2对应可行域在圆O中存在交集的平均概率近似为

在假设C4下，角度观测误差被忽略，则单雷达站对应可行域如图7所示，其中阴影区域的边界平行，又因为假设各雷达站对应的速度误差限相同，因此各雷达站对应的可行域宽度相同且均为2Δvmax，进而也不难证明S1,S2对应可行域交叠形状为菱形，大致图像如图8所示。由位置关系可知，S1,S2对应可行域交叠呈的菱形在vy轴上的投影长度为

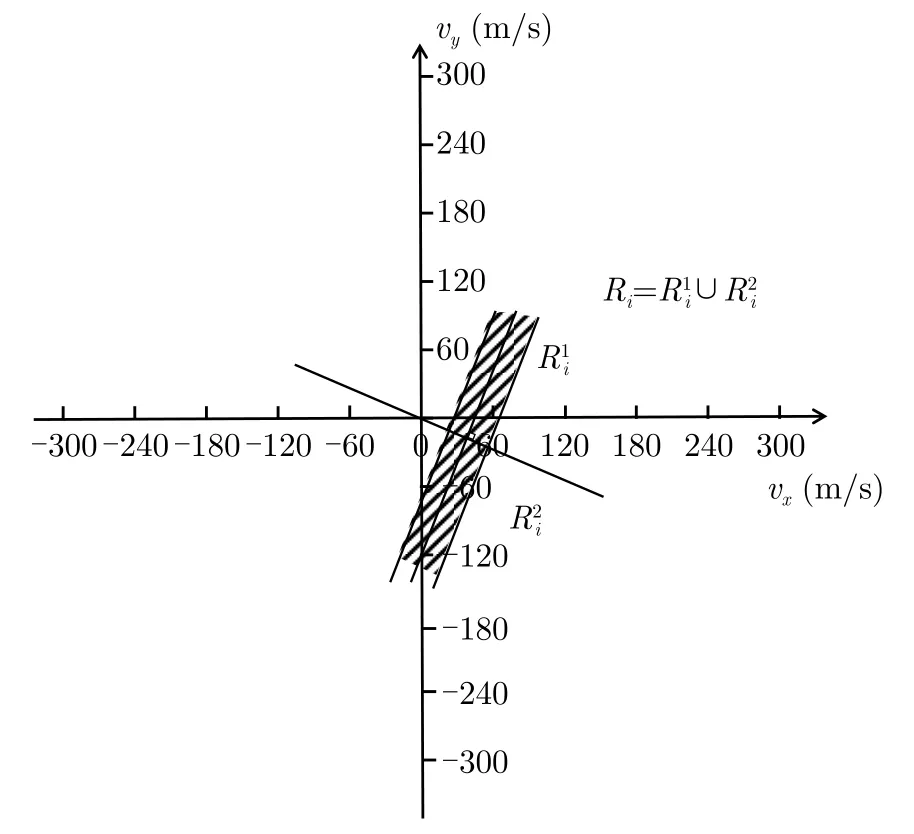
图7 单雷达站对应可行域RiFig.7 Corresponding feasible region R =i of single radar station

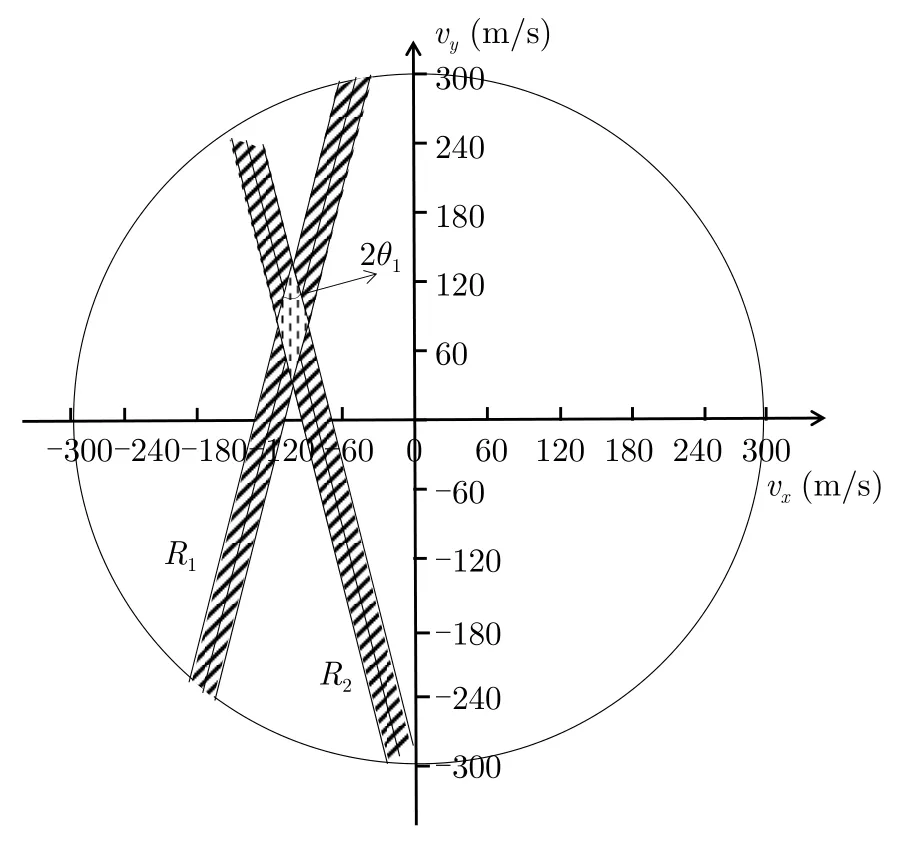
图8 S1,S2对应可行域RFig.8 Feasible region R of S1 and S2

此时由于假设C3的存在，雷达站S3对应的可行域大致与vy垂直，此时3雷达站对应可行域存在交叠情况下S3对应L3可能存在区域如图9所示，并且根据图9中标识的位置关系可推导出：

图9 S3对应L3可能存在区域Fig.9 Possible region of L3 of S3

进而S3对应可行域与S1,S2交叠成的菱形有公共区域的平均概率近似为

综上，在图4所示的3雷达站系统下，且在假设C1—C4成立条件下，虚警满足式(13)—式(15)的概率为

假设基于幅度信息融合检测算法的虚警概率为Pfi，则根据该结果可计算出所提算法最终的虚警概率：

可以看出，所提算法的虚警概率随着 Δvmax的增大而增大，随着vmax的增大而减小，且当θ1max在某一正区间 (0,θ0](θ0＞=0)内时随着θ1max的增大而增大。从各雷达站对应可行域的交叠情况来看，在假设C1—C4下，Δvmax的增加会增大可行域的宽度，vmax的减小会缩小S3对应L3的纵轴截距的分布范围，使得虚警情况下各雷达站的可行域出现交叠的概率增加，从而增大了最终的虚警概率，与式(24)理论结果一致。在假设C1—C4下，当θ1max值为0时，雷达站S1和S2对应的L3平行，两者有交点的概率为0，又由概率值的非负性可知，当θ1max在某一正区间 (0,θ0](θ0＞0)时，算法虚警概率随θ1max单调递增，同样与式(24)理论结果一致。

3.3 算法计算复杂度分析

据3.1节对算法流程的介绍可知，算法遍历每个雷达站对应的子线性不等式组以及可能的速度模糊数建立新的线性不等式组LI，从而利用两阶段法的第1阶段判断其是否有可行域。实质上，两阶段算法的第1阶段是在原优化模型的线性约束中加入人工变量，并以人工变量的和为优化模型建立了新的优化模型，从而利用单纯形算法对其进行求解，通过判断最优值是否为0来判断原线性约束条件是否有可行域。根据文献[29]，单纯形算法的平均复杂度为O(h3m(h-1)-1)，其中h和m分别表示优化变量和线性约束的个数。

对于本算法中线性不等式组LI而言，为将其化为线性规划约束条件的标准形式[24]，需要将符号未知的vx,vy化为

之后在两阶段算法中会再为线性约束条件加入m个人工变量，因此LI对应的h=4+m，又由式(13)—式(15)可知m=3N，进而得到利用两阶段法判断LI 是否有可行域的平均复杂度为。

考虑最坏情况，每历经一次算法都需要对2N(2K+1)N个可能的LI进行有无可行域的判决，则算法的整体平均复杂度为O((4K+2)N(4+3N)3。

4 仿真实验及分析

从3.1节所提的约束可以看出，所提算法使用的角度与径向速度观测之间有较强的非线性耦合关系，其在不同场景下带来理论的检测性能难以通过直接积分的方式解析计算，因此本节通过蒙特卡罗试验对所提方法的性能及其影响因素进行分析验证，针对某一网络化雷达系统对多普勒信息辅助的融合检测算法进行实验仿真，假设各雷达站发射波形均为线性调频信号(Linear Frequency Modulation,LFM)，各雷达系统主要参数如表1所示。假设影响各雷达检测的因素均为高斯白噪声，其功率参数相同。假设网络化雷达共视区域为50 km×50 km的正方形，其形状如图10中阴影部分所示，目标随机出现在雷达共视区域中。

表1 仿真实验雷达系统主要参数Tab.1 Main parameters of the radar systems in the simulation

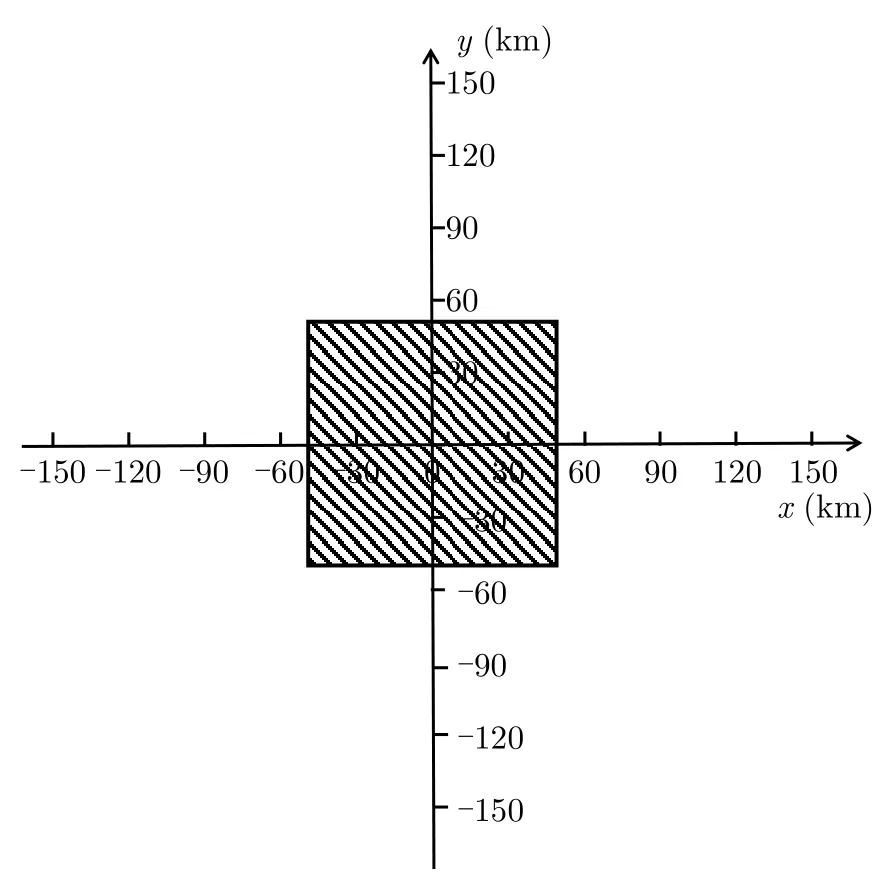
图10 网络化雷达共视区域Fig.10 Radar network common view area

另外，实验中假设雷达对角度和速度的量测误差均服从高斯分布，且均值均为0，其标准差正比于瑞利分辨率，且反比于回波信噪比[30]。对于目标，实验中假设最大飞行速度为vmax=300 m/s，飞行方向为任意角度。最后，没有特别提及情况下传统融合检测选用最优融合检测器Topt。用于估计待检测单元的参考窗长n=8，传统融合检测算法和本文所提算法最终的虚警概率均固定为Pfa=10-3，其中所提算法虚警概率通过蒙特卡罗实验法得到。不失一般性地，假设各雷达站观测到目标的信噪比相同，此时前述式(6)与式(7)的融合检测器性能相同。

4.1 融合检测性能对比

根据第3节的分析可知，所提多普勒信息辅助的融合检测算法实质上通过保证较小的检测概率损失的同时，降低了虚警概率，等价于在最终虚警概率相同的条件下提升了目标检测性能。若设传统融合检测器的检测门限值为γ，在给定融合检测器的检验统计量TF(Z)及其在 H0和 H1假设下的概率密度函数时，该检测器虚警概率为，输出检测概率为，且均随着γ的升高而降低[2]。经过所提算法二次判断之后的虚警概率和检测概率分别为

其中，rfa表示本文算法带来的虚警排除率，ld表示检测概率损失率。若固定系统虚警概率Pfa=α，则算法最终输出检测概率为

为检验算法的可靠性，现基于本文算法，在3雷达站系统下，利用多普勒信息分别辅助最优融合检测器Topt以及实际应用中较易于实现的求和规则检测器Tsum和服从求“或”准则的融合检测器进行融合检测[31]，得到引入多普勒信息进行辅助检测前后，融合检测器的检测性能对比如图11所示。可以看出，引入多普勒信息辅助检测后，最优融合检测器Topt、求和规则检测器Tsum和服从求“或”准则的融合检测器的检测性能均得到了有效的增益，这也与前述分析相吻合。

图11 各种传统融合检测器引入多普勒信息辅助检测前后的检测性能Fig.11 Detection performance of various traditional fusion detectors before and after the introduction of Doppler information

4.2 雷达站个数对检测性能的影响

3.2节已经给出了单雷达站对应可行域的示意图，如图3所示。对于两雷达站系统而言，无论是否存在目标，其对应的两条观测值下L3总会有一个交点，即使两直线平行，其对应的R1,R2总会有公共交集，如图12所示。也就是说，使用所提算法在该场景下一定会判定目标存在，无法对传统融合检测结果加以修正。因此，对于仅使用两个雷达站的网络化雷达系统，所提算法无法改善传统融合检测的检测性能。

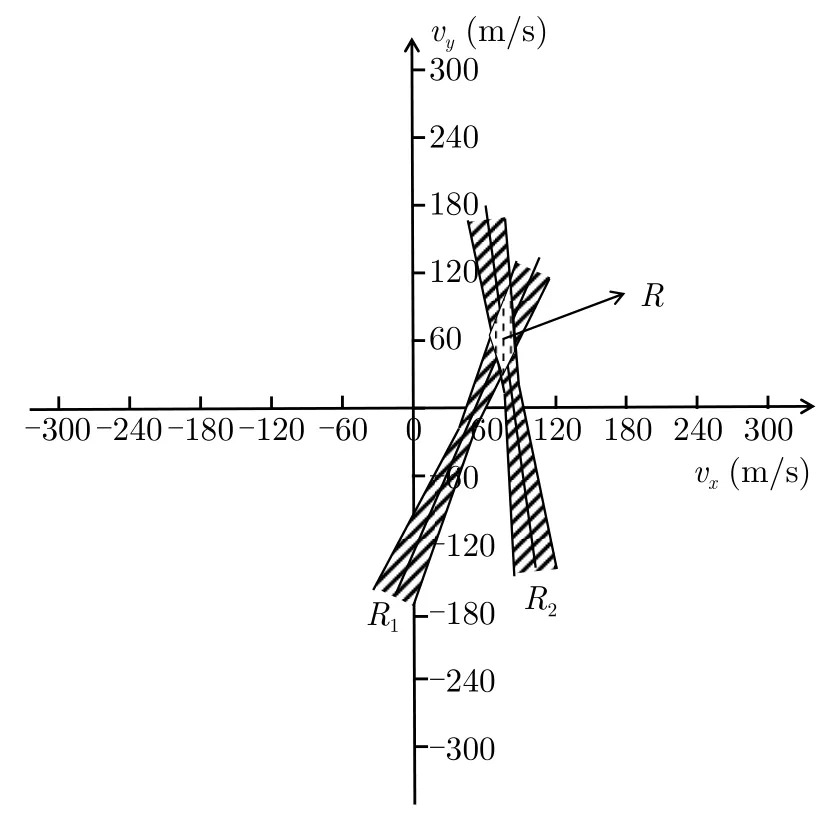
图12 两雷达站系统对应可行域RFig.12 Feasible region R based on dual-radar station system

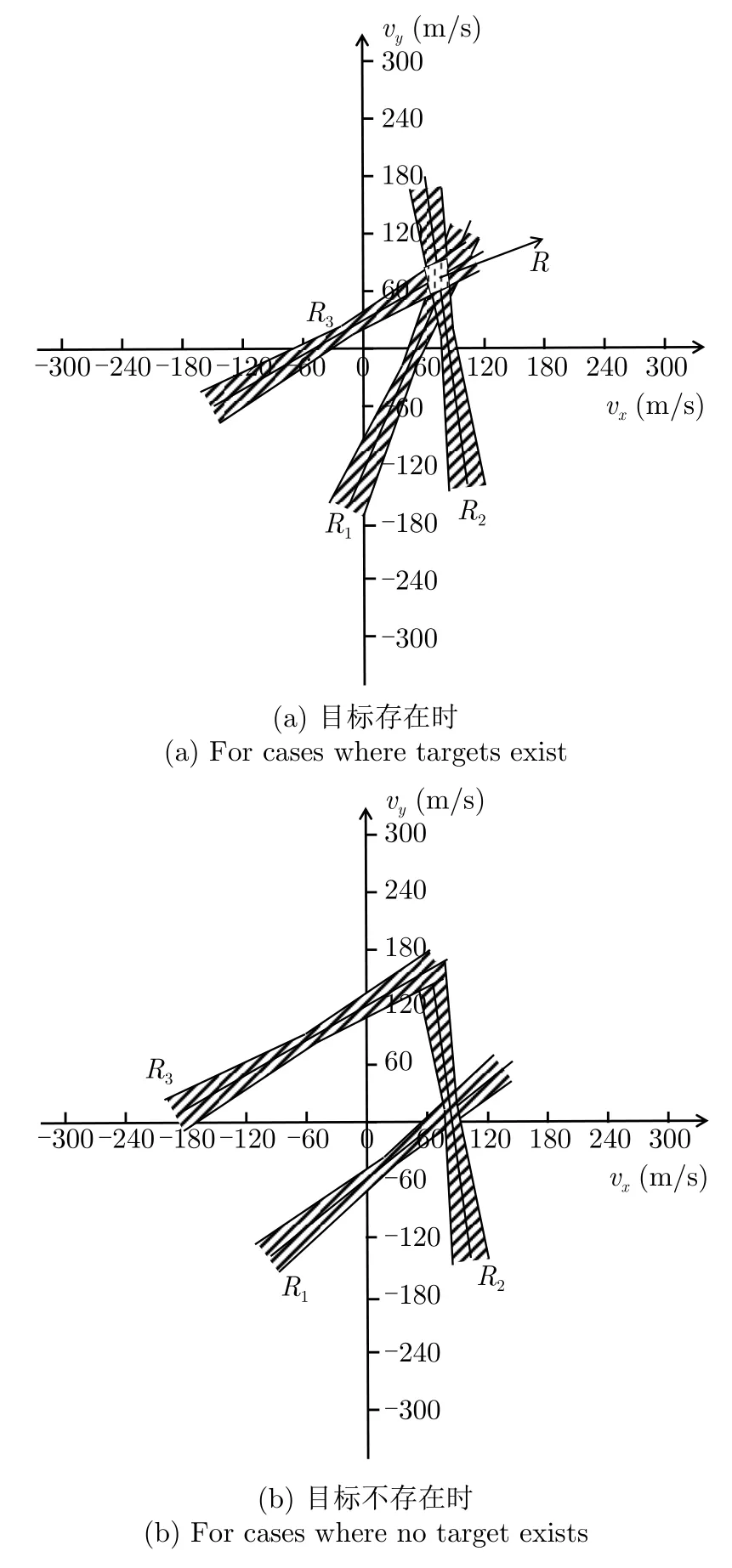
图13 3雷达站系统对应可行域RFig.13 Feasible region R based on three-radar station system

为验证上述结论，基于表1雷达系统参数，下面对包含2,3以及4部雷达站系统的网络化雷达系统场景进行仿真实验，雷达布站位置如图14所示，不同网络化雷达系统下检测性能曲线如图15所示。可以看出，图15所示的实验结果与前述分析基本一致：除两部雷达站的网络化雷达系统外，3雷达站系统与4雷达站系统的检测性能均在引入多普勒信息后得到了明显增益。对于低信噪比目标，检测性能提升更加明显。这说明了多普勒信息带来的信息增量能够提高雷达系统的检测性能。需要注意的是，图7在4雷达站系统上应用算法后，检测概率几乎为1，这是由于共视区相对于各雷达站位置较为理想，且实验中为便于比较而设置了较高的虚警概率。这使得在蒙特卡罗次数较少的条件下，几乎在所有的实验中目标均能够利用多雷达站的冗余信息得以正确检测，因此会出现检测概率接近1的情况。

图14 雷达布站位置Fig.14 Location of radar stations

图15 不同雷达站个数下算法的检测性能曲线Fig.15 Detection performance of different algorithms applied for scenes with different number of radar stations

通过以上实验结果及分析不难发现，在目标不存在时，随着雷达站数的增多(N≥3)，多雷达站对应的具有公共交集的概率会逐渐变小，出现虚警的概率也会降低，使得同样虚警概率条件下检测性能会逐渐提高。

4.3 雷达布站位置对检测性能的影响

在实际应用中，雷达站的布站位置往往是影响网络化雷达系统探测性能的关键因素。为较好地分析该因素对所提算法性能的影响，不失一般性地，下面在3雷达站的网络化雷达系统中分析所提算法的性能。此外，为分析方便，不妨将3部雷达站放置在半径为150 km的圆上，且将之连线得到的图形设定为关于y轴对称的等腰三角形。为方便评估不同布站位置条件下的融合检测性能，不失一般性地，分别将顶角设置为 30°,60°,90°,120°，如图16所示。

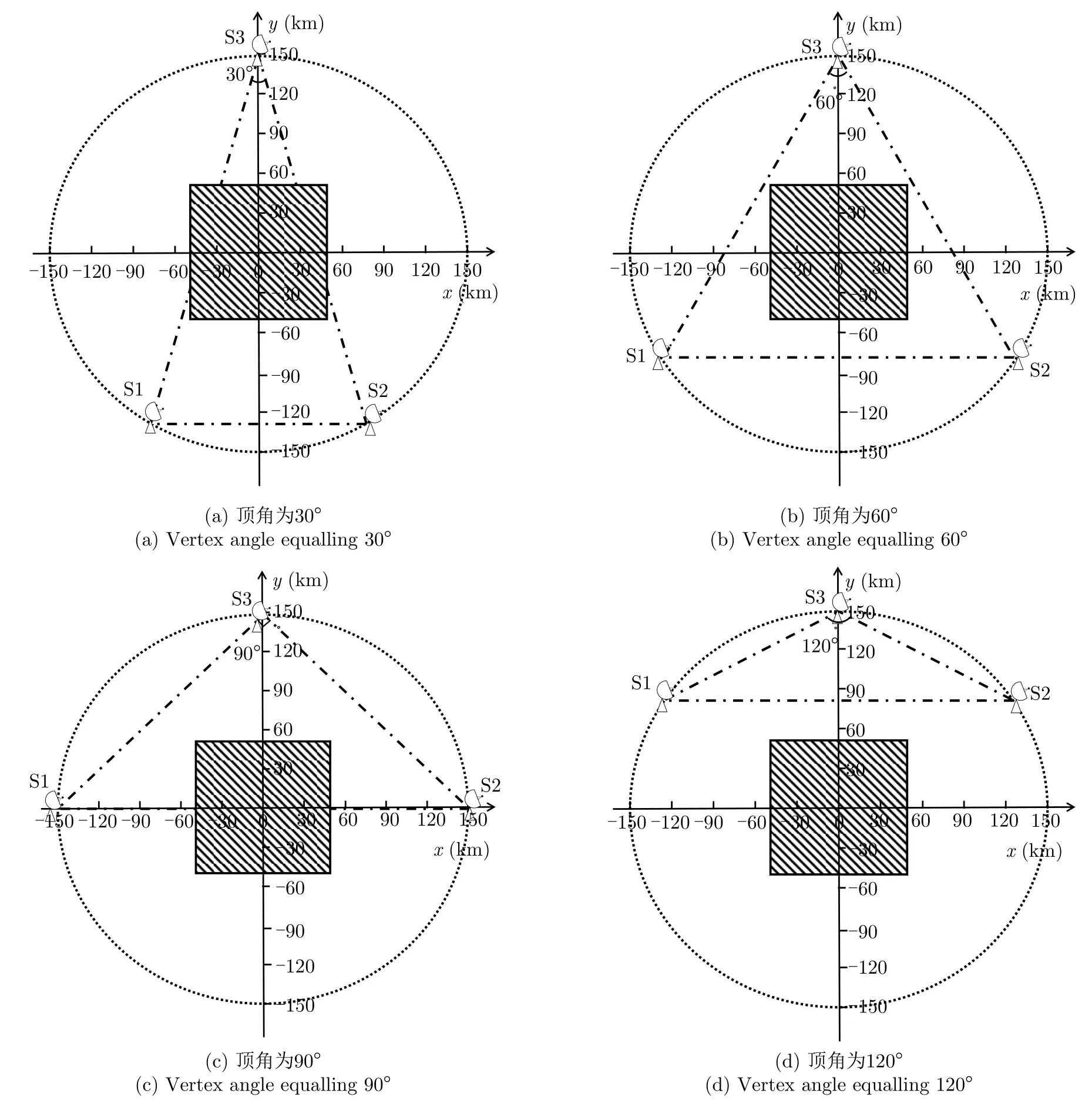
图16 3个雷达站顶角不同时对应的各雷达站位置Fig.16 Locations of 3 radar stations with different top angles

在目标不存在的情况下，通过将雷达站相对于共视区域的位置代入式(8)进行分析，可以得到雷达S3对应的R3大致平行于x轴，与y轴交点集是大致分布在不模糊速度区间内的随机值。当雷达站组成的等腰三角形的顶角较大或较小时，雷达S1与S2对应的R1,R2也均大致平行于x轴，与y轴交点集是大致分布在不模糊速度区间内的随机值，如图17(a)所示，此时3雷达站对应的相近性使得其具有公共区域的可能性较高，虚警满足线性不等式组式(13)或式(14)约束条件的概率会比较大，因此检测性能较差；当雷达站组成等腰三角形的顶角接近90°时，雷达S1与S2对应的R1,R2均大致平行于y轴，与x轴交点集是分布在不模糊速度区间内的随机值，如图17(b)所示，此时3雷达站对应的具有公共区域的可能性较低，虚警满足线性不等式组式(13)或式(14)约束条件的概率较小，检测性能较好。

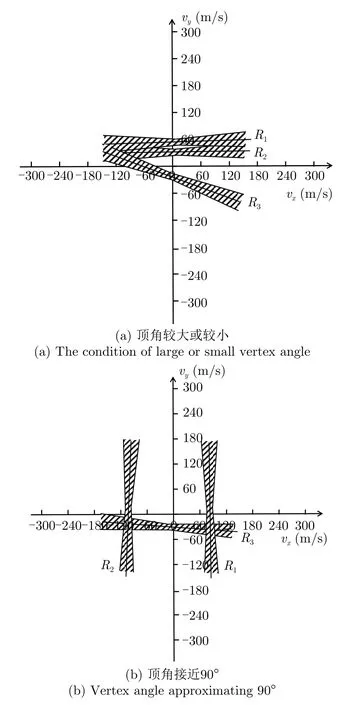
图17 不同雷达布站位置下的分布图Fig.17 Distribution of based on radar systems with different locations of radars

为验证上述分析结果，保持表1中雷达基本参数不变，在图16所示的雷达系统上应用所提算法，得到不同布站位置下检测性能曲线如图18所示。可以看出，实验结果与前述分析基本一致，随着雷达布站连线所呈等腰三角形的顶角由小变大(30°～120°)，网络化雷达系统的检测性能经历了由劣变好再衰退的过程，并且在顶角为 90°时达到最佳。

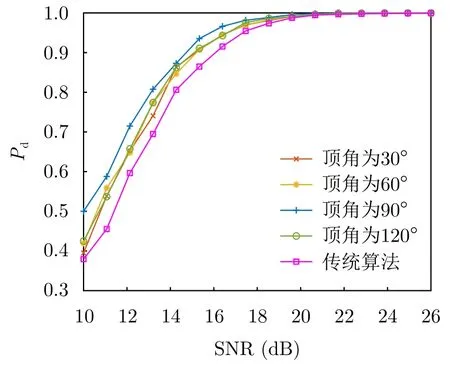
图18 不同雷达布站位置下检测性能曲线Fig.18 Detection performance of algorithm applied in radar systems with different distributions of radars

基于以上对3雷达站系统下布站位置对检测性能的讨论，不难推论，当两雷达站关于共视区域中心点对称，且关于共视区域中心点对称的雷达对在分布圆上等间隔分布时 (若雷达站数为奇数，则无法组成雷达对的雷达站随机分布在相邻两雷达站的中心)，目标不存在时相对应的出现交叠区域的可能性比较小，此时网络化雷达系统的检测性能可以达到最佳。

4.4 目标位置对检测性能的影响

根据前述分析可知，除雷达站布站位置外，目标相对于雷达站所处的位置也即感兴趣的检测点位置也是影响融合检测性能的重要因素。假设选用3雷达站连线构成的等腰三角形顶角为 90°的雷达布站系统，目标按如图19分布。在目标不存在的情况下，通过将图19中雷达站相对于共视区域的位置代入式(8)进行分析，可以得到检测点在处于不同位置下各雷达站对应的分布如图20所示。

图19 目标位置Fig.19 Location of targets

图20 不同目标位置下的分布图Fig.20 Distribution of based on radar systems with different locations of the target

为验证该分析，保持表1雷达基本参数不变，在图19所示的雷达系统上应用所提的算法，得到不同目标位置下检测性能曲线，如图21所示。当目标位置处于y轴上且从共视区域的上边界逐渐转移到下边界时，以及目标从共视区域下边界的左边界转移到右边界时，网络化雷达系统的检测性能经历了由劣变好再衰退的过程，并且当目标接近共视区域的中心时检测性能会更好。根据以上分析及实验结果不难推论，在4.2节讨论得出的最佳布站位置的基础上，当目标处于各雷达站连线所构成图形的中心时检测性能可达到最佳。

图21 不同目标位置下检测性能曲线Fig.21 Detection performance of algorithm applied in radar systems with different locations of targets

5 结语

针对传统融合检测算法未充分利用多雷达站回波信息的问题，本文提出了多普勒信息辅助的融合检测算法。该算法基于多雷达站观测到同一目标的角度与速度信息的物理约束设计了角度与速度信息耦合的不等式组，并采用两阶段法对该不等式组是否有解做出判断，从而进行融合判决。所提的方法在传统仅基于幅度信息融合检测的基础上，引入多普勒信息辅助检测，利用多雷达站冗余的观测信息进一步区分目标和虚警。从而在保持最终虚警概率恒定的前提下有效降低了幅度融合所需的检测门限，提高检测性能。

此外，本文通过对设计的角度与速度信息耦合不等式组对应的可行域进行可视化，分析了所提算法在雷达数量不同、雷达布站位置不同以及目标位置不同等场景下的检测性能，通过仿真实验验证了该分析。该可视化结果能够直观地给出所提算法在不同应用场景下的检测性能。但是，由于所提算法使用的角度与径向速度观测之间有较强的非线性耦合关系，本文只给出了特定假设条件下的理论检测性能分析结果，更具普遍意义的理论分析还需要借助更复杂的数学工具才能实现，这也是下一步的研究方向。