基于脉冲交错的分布式雷达组网系统波束驻留调度
2023-07-04恒思宇李中柱
程 婷 恒思宇 李中柱
(电子科技大学信息与通信工程学院 成都 611731)
1 引言
随着现代战场环境的日益复杂,分布式组网雷达因具有较单雷达系统更优的目标检测、参数估计、多目标跟踪以及干扰抑制等性能,受到广泛关注和研究[1–3]。为充分发挥分布式组网雷达系统的作战效能,实现系统资源在多雷达任务之间的合理分配,如何设计有效的波束驻留调度算法是关键。
现有的雷达波束驻留调度算法研究主要针对单雷达系统展开。文献[4]针对相控阵雷达提出一种基于时间指针的波束驻留调度算法,其中综合考虑任务的截止期和工作方式优先级形成动态优先级,在各个分析时刻调度综合优先级最高的任务。文献[5]在动态优先级的设计中考虑了目标的威胁度,以此为基础,设计了一种在线波束驻留调度算法获得了相应的实际调度序列。文献[6]提出了一种双边波束驻留调度算法,该算法在调度分析的时间段上设置分隔点,并在分隔点的两侧分别以截止期最早原则和起始时间距分割点最近原则调度波束驻留任务。文献[7]在波束驻留调度问题建模中提出了任务调度收益这一概念,并采用一种基于调度间隔分析的方法设计能使得该调度间隔获得最大收益的调度时序。文献[8]设计了成像任务的优先级,并以一种启发式调度方法实现了雷达搜索、跟踪和成像任务的调度。在文献[9]中,可变时间窗的概念被引入,并设计了基于可变时间窗的相控阵雷达波束驻留调度算法,使得跟踪任务的实际执行时刻调整范围进一步增大,系统的调度成功率得到提升。文献[10,11]分别在相控阵与数字阵列雷达下的波束驻留调度中引入了脉冲交错技术,在相控阵雷达中有效利用了各个跟踪任务的等待期,在数字阵列雷达中跟踪任务的等待期和接收期均被充分利用,使得系统的时间利用率得到进一步提高。近几年来,随着计算机性能的提升,各类智能搜索算法以及人工智能技术得到飞速发展,这些技术也被用于解决雷达波束驻留调度问题。文献[12]提出了基于价值优化的波束驻留调度模型,并采用遗传算法获得了该问题的最优解,获得了对应的最优调度序列。针对超声速目标跟踪下的波束驻留调度问题,文献[13]采用基于粒子群-模拟退火的算法解决了这一问题。文献[14–16]分别采用禁忌搜索和强化学习的方法解决波束驻留调度问题。文献[17–19]分别引入混合自适应遗传算法、基于熵理论的粒子群算法、离散粒子群-列维飞行算法解决了相控阵、数字阵列以及MIMO雷达引入脉冲交错下的波束驻留调度问题。
在分布式组网雷达系统的波束驻留调度中,除波束驻留任务的实际执行时刻外,还需确定具体执行波束驻留任务的雷达节点。文献[20]以多流水线调度问题模型为基础,获得了多通道雷达波束驻留调度问题的模型,并采用截止期最早原则与分支定界法(Branch and Bound,B&B)分别获得了各通道上的任务调度序列。文献[21]训练了一个三层神经网络,该神经网络可加速B&B的剪枝速度,以提升多通道雷达波束驻留调度算法的分析速度。文献[22]则采用蒙特卡罗搜索树获得多通道雷达的实际执行任务队列。文献[23]参照市场拍卖的过程为雷达波束驻留任务设计了综合优先级,并采用一种启发式方法解决了组网雷达系统的波束驻留调度问题。在文献[23]的基础上,文献[24]针对周期相互独立而不具有倍数关系的多任务,提出了一种广义的雷达组网波束驻留调度算法。文献[25]提出了一种基于内点法的组网雷达波束驻留调度算法,该方法允许对驻留时间进行压缩,进一步提升了系统的调度性能。文献[26]将多功能雷达组网系统的波束驻留调度问题建模为一个马尔可夫决策过程,并提出了一种基于Q学习的波束驻留调度算法。文献[8]仅针对单站雷达考虑成像任务的调度问题,文献[27]将上述问题拓展至组网雷达之中,并提出一种基于凸优化的调度算法解决了任务同雷达节点的匹配问题。进一步,文献[28]将文献[27]所提出的组网雷达波束驻留调度问题抽象为一潜在博弈问题,并在文献[29]中采用多代理强化学习的方法解决了该博弈问题,获得了相应的任务调度序列。
上述分布式组网雷达系统下的波束驻留调度虽然取得了一系列成果,但仍存在以下问题:
(1) 基于启发式方法的分布式组网雷达系统波束驻留调度方法[20,23,24],虽然可以实现实时的波束驻留调度,但调度序列中实际执行任务排布不紧密,系统的时间资源未被充分利用的问题,调度性能不佳;
(2) 基于智能算法的分布式组网雷达系统波束驻留调度方法,虽然调度性能有保证,但算法的运算量过大,调度算法不具有实时性,因此,无法在实际分布式组网雷达系统中适用;
(3) 现有的分布式组网雷达系统波束驻留调度算法[20–29]中,均将驻留任务视为非抢占式任务,未能够充分利用跟踪任务的等待期,造成了时间资源的浪费。在作者的认知中,目前尚未有人提出考虑脉冲交错的组网雷达系统波束驻留调度算法。
针对上述问题,本文提出了一种基于脉冲交错的实时分布式组网雷达系统波束驻留调度算法,主要创新点包括:
(1) 通过引入时间指针向量以提高分布式雷达组网系统的时间利用率,将在时间指针向量指示时刻具有最高综合优先级的波束驻留任务分配至时间利用程度最低的雷达节点处,因此本算法可充分利用各个雷达节点的时间资源。此外,因为有时间指针向量的引入,本算法所得各雷达节点的实际执行任务队列可紧密排列,进一步提高了算法的时间利用率。
(2) 通过引入脉冲交错分析以实现具有不同脉冲重复周期和脉冲重复个数的任务在不同雷达节点上的脉冲交错。本文通过时隙占用矩阵和能量消耗矩阵中的元素值来反映各个雷达节点的时间与能量资源使用情况,从而用于简化脉冲交错的判断条件分析。
(3) 为解决引入脉冲交错分析带来的算法复杂度,引入了时间利用阈值以加快时间指针的滑动速度,从而有效提高了算法的执行效率,保证了波束驻留调度算法的实时性。
2 分布式雷达组网系统的波束驻留调度问题建模
假设分布式雷达组网系统中包含M个多功能雷达R=[R1R2...RM],其中各个雷达节点工作在跟踪加搜索(Track and Search,TAS)的单波束模式下,多雷达协同完成监测区域的搜索和多目标跟踪任务,每个波位的搜索任务和各目标的跟踪任务可由任何一个雷达节点完成。另外,本文不考虑多部雷达同时跟踪单个目标的情况。在分布式雷达组网系统中,系统前端和处理模块按照设定的调度间隔进行数据交换。一方面,处理模块对上一调度间隔各个雷达节点收到的回波信息进行处理,形成后续波束驻留调度任务请求;另一方面,处理模块在系统前端资源约束条件下,形成下一个调度间隔各个雷达节点的波束驻留任务执行序列。对于下一个调度间隔无法执行的波束驻留任务,判断是否延迟执行还是进行删除,延迟任务加入至下一个调度间隔的申请调度任务之中。图1给出了分布式雷达组网系统的波束驻留调度结构。

图1 分布式雷达组网系统波束驻留调度结构示意图Fig.1 Schematic diagram of dwell scheduling structure of distributed radar network system
雷达波束驻留任务采用不同的任务参数进行描述,对于任务Ti的模型如下所示:
其中,Wi为工作方式优先级,dti为期望执行时刻,li为时间窗,驻留任务的最早可执行时刻与最晚可执行时刻分别为dti-li和dti+li,txi代表任务的发射期,twi为等待期,tri为接收期,prii为脉冲重复周期,Mi为脉冲重复周期的个数,Pti为发射功率。
2.1 分布式雷达组网系统波束驻留调度的约束条件
假设在当前调度间隔[t0,t0+tSI]内有N个波束驻留任务T=[T1T2...TN]申请在分布式组网雷达系统上调度执行,其中,t0为当前调度间隔的起始时刻,tSI为 调度间隔的时长。波束驻留调度算法需确定该调度间隔中被调度执行任务的实际执行时刻、执行雷达节点,以及删除和延迟至下一调度间隔的任务。将该调度间隔第p个雷达节点的实际执行任务数量记为,被延迟的任务数量记为N2,被删除任务数量记为N3,则
对于其中被调度执行的任务,其实际执行时间应该满足时间窗的约束,即
其中,ati代表第i个被调度执行任务的实际执行时刻,N1为所有雷达节点上实际执行任务数量的总和,即N1=。
由于被跟踪目标的距离可根据滤波器输出的目标状态估计结果预测获得,因此,跟踪波束驻留任务的等待期可由目标的预测距离计算得到。在某个跟踪波束驻留任务的等待期中,可以去执行其他目标跟踪任务的波束发射或者是回波接收,即进行脉冲交错。在此过程中,不同跟踪任务的发射期之间、接收期之间、发射期与接收期之间不存在时间资源上的冲突,即
需要提及的是,搜索任务不具有目标状态估计信息,发射期过后进入接收期,因此,无法进行脉冲交错。
除时间资源约束外,由于脉冲交错会导致系统持续发射波束的时间正常,因此,还需要满足能量约束:
其中,Ep(t)为雷达节点Rp在t时刻的能量消耗值,可由式(8)计算:
其中,Pp(t)为雷达节点Rp的辐射功率函数,τ是回退参数,反映了系统的散热性能。
在本调度间隔内被延迟执行或删除的任务分别满足以下两条约束条件:
其中,式(9)表示延迟任务的最晚可执行时刻不小于本调度间隔的结束时刻,因此,有机会在后续调度间隔中被调度执行,而式(10)则代表删除任务已无法在后续的调度间隔内被执行。
2.2 分布式雷达组网系统波束驻留调度的优化模型
波束驻留调度需要遵循两个准则,即重要性准则和紧迫性准则。重要性准则意为雷达系统应调度尽可能多的高工作方式优先级任务,而紧迫性准则意为截止期早的任务应尽可能被优先执行。根据驻留调度的这两项准则,针对每个波束驻留任务构建如下调度收益函数:
其中,g1(Wi)是一个随任务工作方式优先级单调递增的函数,工作方式优先级越高,该函数取值越大,所以这一项体现了调度的重要性准则;g2(dti,li,t0)是一个随截止期单调递减的函数,截止期越小,该函数取值越大,因此这一项体现了调度的紧迫性准则,例如,
上述两个函数为合理的工作方式优先级函数和截止期函数,其中,g2(dti,li,t0)中的c1为一个正的常数。因波束驻留调度需同时满足以上两条准则,所以在本文中以相乘的形式构造了Gi(dti,li,Wi,t0)。
分布式雷达组网系统在波束驻留调度过程中获得的总收益,可以表示为被所有雷达节点调度任务的调度收益之和,即
基于上述波束驻留调度目标函数以及约束条件,可建立如下的分布式组网雷达波束驻留调度的优化问题模型:
其中,ri为执行任务Ti的雷达节点序号。优化问题(15)中的可优化变量反映了当前调度间隔内实际执行任务队列、延迟任务队列以及删除任务队列的基本属性。一旦确定了本调度间隔内需要执行、延迟以及删除的任务,就可以根据实际执行任务的期望执行时刻 dti、时间窗li、工作方式优先级Wi以及当前调度间隔的开始时刻t0计算目标函数(14)。
以上优化问题为一典型NP难问题。该优化问题有两个难点,一是求解过程应该具有实时性,这是波束驻留调度问题的本质所要求的,且优化结果应尽可能充分利用每部雷达的时间资源;二是约束条件中的脉冲交错判断条件过于复杂,在优化求解中如何在线实现多雷达节点脉冲交错的分析,并同时保证引入脉冲交错分析后的波束驻留调度算法仍具有实时性。
3 基于脉冲交错的分布式雷达组网系统波束驻留调度算法
为解决上述优化问题,本文提出了一种基于脉冲交错分析的实时分布式雷达组网系统波束驻留调度算法,该算法基于分布式雷达组网在线脉冲交错分析,并引入时间指针向量,在调度分析时刻将最高综合优先级的波束驻留任务分配给时间利用率最低的雷达节点,下面对算法中提出的在线脉冲交错分析方法及算法步骤进行详细阐述。
3.1 分布式雷达组网系统的在线脉冲交错分析

图2 时隙占用矩阵S与相应的时间资源约束判断Fig.2 Time slot occupation matrix S and corresponding time resource constraint judgment
现在分析任务Ti能否被雷达R2调度,执行过程中可与已经调度执行的任务脉冲交错。为表征任务Ti在时间指针 tp2所指时刻调度于雷达R2上的时间占用情况,我们引入了时间变化向量,时间变化向量的各个元素的计算公式如下所示:
将ΔS2同S的第2行逐元素相加,依据式(17)判断脉冲交错过程是否会产生时间资源冲突:
如果存在元素大于1,表明Ti使用了已经被占用过的时间间隙,Ti不可在 tp2所指时刻调度被雷达R2调度;若所有元素均小于等于1,则说明Ti未使用过已经被占用过的时间间隙。如图2右侧所示,可以看到Ti的发射期与接收期同之前所执行的任务没有冲突。
由于脉冲交错会导致系统发射期持续时间增长,需要进一步判断能量约束是否被满足。在调度间隔的初始分析阶段,各雷达节点的能量使用情况由每个雷达节点在上一个调度间隔结束时刻的能量使用情况所决定,即能量消耗矩阵E中第j行、第n列所对应元素Ej(n)初始化如下:
其中,ΔE2k(n)由式(20)计算:
若要判断任务Ti是否满足能量约束,将ΔE2同E的第2行逐元素相加,依据式(21)进行分析即可:
其中,Eth为能量约束判断阈值。若存在元素的值超过Eth,则说明不符合能量约束条件;若所有的元素均未超过Eth,则说明符合能量约束条件。若时间约束与能量约束均符合条件,则说明该驻留任务可以交错执行在被分析的雷达节点上。
3.2 引入脉冲交错的分布式雷达组网系统波束驻留调度算法
由于整个雷达组网系统具有多个雷达节点,系统具有多个并行的时间轴,调度分析时刻不具有唯一性。为解决这一问题,引入时间指针向量tp表征各个雷达节点的当前调度分析时刻。如图3所示,tp=[tp1,tp2,tp3],其中,tpj为雷达节点Rj的时间指针。对于时间指针向量tp,选取满足以下条件的任务集合:
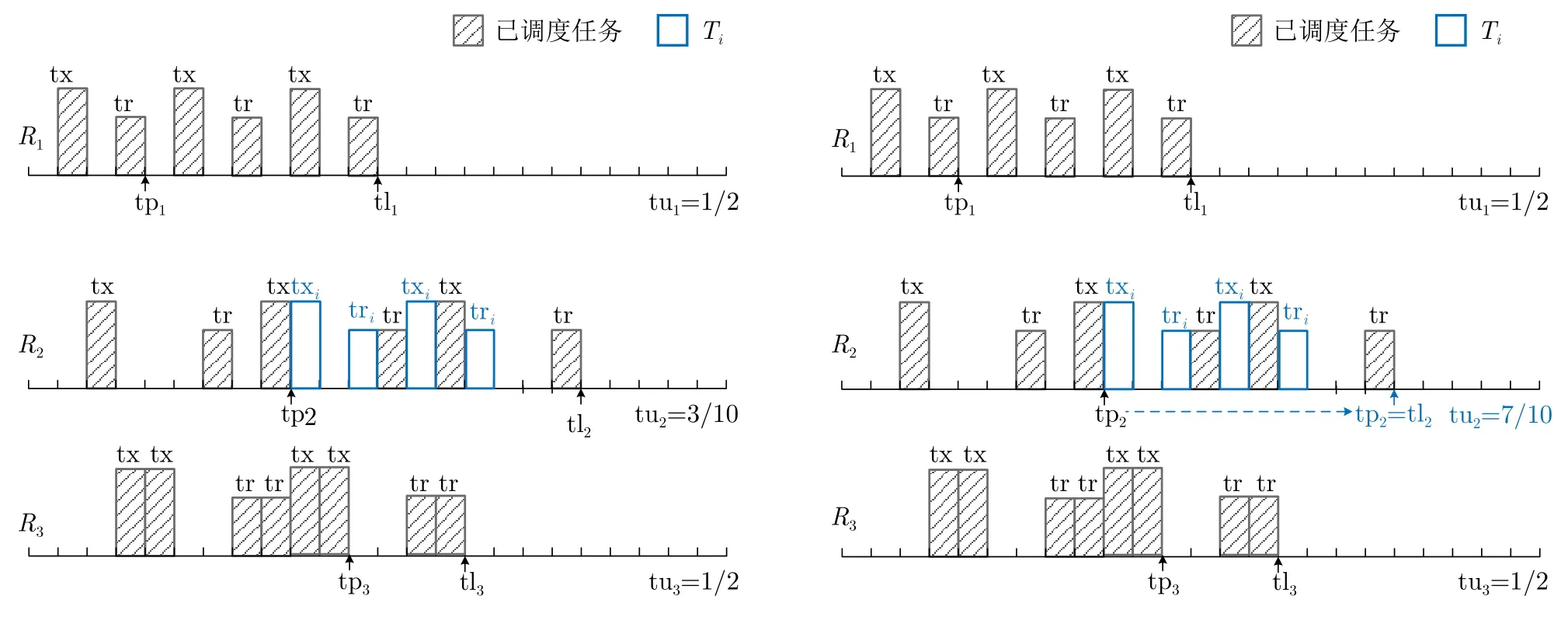
图3 分布式雷达组网系统波束驻留调度算法示意图Fig.3 Schematic diagram of dwell scheduling algorithm for distributed radar network system
可以看到,满足上述条件的任务是可能在tp指示的某个或者某几个雷达节点执行的任务。
根据式(15)所示的优化问题模型,目标函数是极大化分布式雷达组网系统的调度收益,越重要、越紧迫的任务被调度执行能有效提高系统的调度收益。因此,若在tp表征的分析时刻存在X任务,综合考虑任务的工作方式优先级和截止期,设计如下综合优先级:
其中,Xdi为任务请求Ti(1≤i≤X)在X个任务中按截止期从大到小排列的序号,Xpi为在X个任务中按工作方式优先级从小到大排列的序号。具有较大综合优先级的任务即为工作方式优先级较高且截止期较紧迫的任务,而具有较小综合优先级的任务即为工作方式优先级较低且截止期不太紧迫的任务。因此,在当前时间指针向量所指时刻调度具有最高综合优先级的任务等价于调度具有最高调度收益的任务。对于X个任务,按照所获得的综合优先级高低依次对任务进行考虑脉冲交错的调度分析。
注意到对于被调度分析的任务,可以执行它的雷达节点可能超过1个,考虑到脉冲交错的本质是充分利用已经被调度任务所占用的时间轴上的剩余可用资源,因此,为调度分析的任务选取具有最低交错时间利用率的雷达节点进行脉冲交错分析。雷达节点的交错时间利用率定义为该雷达时间指针与已调度执行任务的结束时刻之间的时间利用率,对于第j个雷达节点的交错时间利用率 tuj可按式(24)计算:
其中,tlj代表雷达节点Rj上已调度执行任务的结束时刻,分别表示 tpj和 tlj在矩阵S的第j行上所在的位置,计算方法如式(25)和式(26)所示:
从图3可以看出,R1,R3的利用率相同且偏高,R2利用率低,假设Ti是被脉冲交错调度分析的任务,则应用3.1节所提的脉冲交错分析方法判断其能否调度于R2上。
在图3所示的示例中,脉冲交错成功,Ti可在tp2时刻被雷达R2调度执行。随后,滑动 tp2至下一个调度分析时刻。传统基于时间指针的波束驻留调度算法,未考虑脉冲交错,时间指针的滑动步长为被调度任务的驻留时长。当考虑脉冲交错时,为充分利用跟踪任务的等待期,时间指针滑动步长可设置为被调度执行任务的发射期长度,但这增加了脉冲交错分析的次数,导致相应调度算法的效率降低。这里提出自适应调整时间指针滑动步长的方法,根据调度Ti后的交错时间利用率判断时间指针应该“大步走”还是“小步走”。定义交错时间利用率阈值tuth,则时间指针的滑动步长按式(27)计算:
在图3右侧可以看到,调度Ti后R2的时间利用率变为0.7,假设设定的 tuth<0.5,则 tp2应滑动至tl2所在位置。
综上所述,下面给出在调度间隔 [t0,t0+tSI]内针对N个波束驻留任务T=[T1T2...TN],基于脉冲交错的分布式雷达组网系统波束驻留调度算法的具体步骤,如表1所示。

表1 基于脉冲交错的分布式雷达组网系统波束驻留调度算法步骤Tab.1 The steps of the dwell scheduling algorithm for distributed radar network system based on pulse interleaving
需要提及的是,通过 min(tp)选出被删除任务的目的是删除掉所有在当前时间指针向量所指时刻及以后无法执行的任务。若任务Ti满足条件dti+li<min(tp),则说明Ti的最晚可执行时刻早于tp中的任意一个元素,即Ti在任意一个雷达节点上均不能够被执行。通过 max(tp)选出当前分析任务的目的是选出当前时间指针向量所指时刻全部可被执行的任务。若任务Ti满足条件max(tp)≥dti-li,则说明至少有一个雷达节点可以执行该任务。
另外,为说明快速移动时间指针向量的有效性,现对本算法的时间复杂度进行分析。本算法的复杂性一共由3部分构成,分别是当前驻留间隔申请调度任务的数量N,组网系统内雷达节点的个数M,以及时隙占用矩阵的长度NSI所决定的。
考虑最坏情况时间复杂度,时间指针向量tp从t0滑动到t0+tSI最多需要移动M×NSI次。这说明在一次调度算法内至多要在M×NSI个时刻点进行驻留调度分析。在每次驻留调度分析中,需要从N个任务中挑选出删除任务,并从N个任务中挑选出可执行任务,这一部分的时间复杂度在最坏的情况下可以认为是N。在挑选出当前时刻可执行任务后,需计算各个任务的综合优先级。因为在任务的综合优先级计算中涉及两次排序操作,这一部分的时间复杂度可认为是Nlog(N)。计算完任务的综合优先级后,需将具有最高综合优先级的任务放入具有最低时间利用率的雷达节点上进行脉冲交错分析。具有最低时间利用率的雷达节点需消耗复杂度为M。在此之后需要形成与最大综合优先级任务相关的时间变化向量ΔS与能量变化向量ΔE,并进行脉冲交错分析,这一部分的时间复杂度可以认为是NSI。因为在一个时刻内的驻留调度分析不存在嵌套操作,所以时间复杂度为加法关系,即O(N+Nlog(N)+M+NSI)。考虑到外层的循环,本文所提出驻留调度算法的时间复杂度在最坏的情况下为O(M×NSI×(N+Nlog(N)+M+NSI))。
注意以上分析并未考虑到加快时间指针滑动对算法时间复杂度的影响。若引入时间阈值以加快时间指针滑动,则外层循环次数将远小于M×NSI,算法的时间复杂度也将显著减小。
4 仿真
场景中考虑存在精密跟踪、普通跟踪、地平线搜索、空域搜索和验证这5种任务,其中,地平线搜索任务有3个区域需要搜索,空域搜索任务同样有3个区域需要搜索,精密跟踪目标数同普通任务目标数之比为1:4,具体的任务参数见表2。假设分布式雷达组网系统中包含3部相控阵雷达,每个雷达均可执行所有的波束驻留任务。采用本文所提的波束驻留调度算法实现分布式雷达组网系统的波束驻留调度,仿真时长为12 s,调度间隔时长设为50 ms,能量阈值Eth设为10J,回退参数τ=200 ms。

表2 雷达波束驻留任务参数表Tab.2 The parameters of dwell tasks
采用任务丢失率(Task Drop Ratio,TDR)、实现价值率(Hit Value Ratio,HVR)、时间利用率(Time Utilization Ratio,TUR)和运行时长作为性能评估指标。任务丢失率(TDR)定义为丢失任务数与申请调度任务数之比:
其中,Ndrop表示丢失任务数,Nall表示申请调度任务的总数。实现价值率(HVR)定义为实际执行任务的工作方式优先级之和与申请调度任务的工作方式优先级之和的比:
其中,Nexe表示实际执行任务数。
值得提及的是,任务丢失率与实现价值率分别同驻留调度的紧迫性准则与重要性准则相关。若在调度过程中未充分调度截止期更为紧迫的任务,则容易出现任务丢失,从而导致任务丢失率偏高;若在调度过程中未充分调度工作方式优先级更高的任务,则所得调度序列的实现价值率将会偏低。若一个驻留调度算法所得调度序列具有低任务丢失率、高实现价值率的特点,则说明该调度算法实现了紧迫性准则与重要性准则,即表明所得调度序列具有极高的调度收益。
时间利用率(TUR)定义为实际执行任务的所有发射期与接收期之和与所有雷达节点调度分析时间轴长度之和的比:
其中,ttotal为总仿真时长,M为分布式雷达组网系统中雷达节点的总数。
首先,对本文所提算法考察不同的交错时间利用率门限的影响。图4给出在不同 tuth下算法性能的对比。从图4可以看到,当 tuth设为0.25时,本算法在目标数为60时即开始出现任务丢失,而当 tuth的值大于等于0.5时,本算法在目标数大于等于120时才开始出现任务丢失,且 tuth的值越大,开始出现任务丢失的目标数越大。类似地,tuth越大,系统的实现价值率越大,时间利用率也越高。这是因为tuth设定得越小,未被利用的剩余时间资源就越多,脉冲交错就越不充分,调度性能越差。另外,tuth设定得越小,时间指针的滑动速度就越快,算法的复杂度就越低,算法的运行时长也就越低,这一点可以由图4(d)中体现出来。当时间阈值在0.5以上时,虽然算法的调度性能仍会随着时间阈值的增大而提升,但性能提升幅度较小。且当时间阈值等于1的时候,算法会有失去实时性的风险。因此综合考虑性能需求以及实时性需求,时间阈值选取为[0.5,0.75]之间比较合理。具体来说,若调度场景中调度性能更为重要,则时间阈值应尽可能接近0.75;若调度场景对实时性要求更高,则时间阈值应尽可能接近0.5。本文在后续仿真分析中均设定tuth为0.5。

图4 不同交错时间利用率阈值下所提算法的性能对比Fig.4 Performance comparison of the proposed algorithm under different interleaving time utilization thresholds
图5给出了本文提出算法在某一次仿真中的部分时序图。其中,较高的矩形为波束驻留任务的发射期,较低的矩形为波束驻留任务的接收期,不同波束驻留任务之间采用了不同的颜色进行区分,且用相同颜色的虚线矩形框将同一个驻留的多个脉冲框在一起。需要提及的是图5中各驻留任务的颜色种类同任务类型无关,仅为了将不同驻留任务的发射期与接收期在图中区分开,以增加该图的可读性。在图5可以看到,本文所提出算法除了在每个调度间隔的结束时刻可能存在时间间隙以外,其余时刻均不存在时间间隙。R1的0~13 ms处、50~68 ms处、88~98 ms处以及R2的30~50 ms处均可以看到出现了脉冲交错,且任务的发射期与接收期之间没有重叠部分。R3上调度任务的发射期与接收期之间没有间隙,即R3调度的任务均为搜索任务。因为搜索任务不存在等待期,所以无法实现脉冲交错。
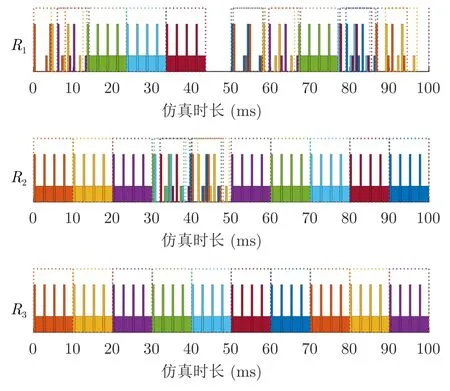
图5 本文提出算法在某一次仿真中的部分时序图Fig.5 Partial task scheduling sequence obtained by proposed algorithm in a simulation
为体现本文所提出算法的优越性,将本文所提算法同算法A与算法B进行对比。其中,算法A为基于最早截止期优先算法的组网雷达波束驻留调度算法[20],并且为了性能对比的公平性,将文献[10]中的脉冲交错分析方法引入至算法A之中。算法B为将表2中的3个地平线搜索任务与3个空域搜索任务分别分配给了各个雷达,并将场景中的目标均分给了各个雷达进行跟踪,随后采用文献[10]中所提出的波束驻留调度算法在tuth=0.5的情况下分别对各个雷达进行驻留级调度。仿真运行平台为MATLAB 2016a,PC 机CPU 为Intel(R)Core(TM) i7-10700,内存为16 GB。相应的仿真对比结果如图6所示。

图6 本文所提算法与算法A、算法B的性能对比Fig.6 Performance comparison between the proposed algorithm and algorithm A &B
可以看到,算法B在目标数为70左右就开始出现目标丢失。这是因为确定好任务与雷达节点的匹配关系之后,可优化的变量仅有驻留的实际执行时刻,与同时优化驻留同雷达节点的匹配关系及实际执行时刻相比,自由度更小。因此,采用这种方法进行调度相对于算法A和本文所提出算法的时间资源利用程度更低,从而导致任务丢失率更高,实现价值率更低。算法A在目标数为90时开始出现目标丢失,而本文所提出算法在目标数为110时才开始出现目标丢失,这是因为将驻留任务调度至具有最低时间利用程度的雷达节点可以更有效地同脉冲交错分析方法相结合,从而提高算法的时间利用率。从图6(d)可以看到,在驻留调度分析过程中确定各驻留同雷达节点的匹配关系会带来额外的计算量,从而导致运行时长提升,但因为本文提出算法的运行时长仍然小于一个调度间隔的长度,所以本文提出算法仍具有实时性,即这一额外的计算量是可以被接受的。另外,算法A的运行时长要高于本文提出算法的运行时长,且当目标个数偏高时,算法A的运行时长超过了一个调度间隔的时长(50 ms),即不具有实时性。这说明了合理的雷达节点同驻留任务的匹配策略不仅可以有效提高算法的时间利用率,同样可以降低算法的运行复杂度。综上所述,与算法B相比,本文提出算法具有更低的任务丢失率、更高的实现价值率以及时间利用率,且本算法相对于算法B带来的额外计算复杂度是可接受的;与算法A相比,本文提出算法除了具有更优的调度性能,还保证了调度的实时性,因此本算法更适用于分布式雷达组网系统的波束驻留调度。
5 结语
有效的波束驻留调度算法是充分发挥雷达组网系统作战效能的关键。本文针对分布式雷达组网系统提出了一种基于脉冲交错的实时波束驻留调度算法。该算法引入时间指针向量表明多个雷达节点的当前调度分析时刻,并在时间指针向量指示时刻将具有最高综合优先级的波束驻留任务分配至交错时间利用程度最低的雷达节点,有效提升了雷达组网系统的时间利用率。为实现分布式雷达组网系统的在线脉冲交错分析,引入了时隙占用矩阵与能量占用矩阵分别表征当前调度间隔内的所有雷达节点时间资源与能量资源的使用情况,这种处理方式不仅简化了脉冲交错分析,而且可实现具有不同脉冲重复周期与个数的任务之间的交错。仿真结果表明,本文所提算法较现有方法能有效降低任务的丢失率,从而使系统获得更高的价值实现率和时间利用率。此外,本算法的调度效率和调度性能还可以通过交错时间利用率门限进行平衡,可以根据实际应用场景灵活调节,具有重要的实用价值。
