一种低截获背景下的集中式MIMO雷达快速功率分配算法
2023-07-04李正杰谢军伟张浩为
李正杰 谢军伟 张浩为* 温 泉 刘 斌
①(空军工程大学防空反导学院 西安 710051)
②(国防科技大学信息通信学院 西安 710106)
③(国防大学联合作战学院 北京 100091)
1 引言
作为一种新体制雷达,集中式多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达引起了研究人员的广泛关注。经过近20年的研究,出现了许多关于参数估计、主动抗干扰、射频隐身等方面的研究成果,并已进入工程实践阶段[1]。相比于传统相控阵雷达全相干的信号发射机制,集中式MIMO雷达可同时发射多个正交信号,从而具备优越的波形分集增益[2]、低截获性能[3]、虚拟孔径[4]以及目标检测性能[5]。为充分发挥多发多收的体制优势,进一步挖掘集中式MIMO雷达的作战潜能,需要对有限的雷达系统资源进行优化分配。
近年来,围绕资源分配技术在目标跟踪上的应用问题,国内外学者基于认知雷达思想[6],逐渐形成了关于雷达资源分配的两大原则[7]:(1)有限资源约束下提高跟踪性能原则[8–16];(2)满足跟踪精度约束下减少资源消耗原则[17–23]。关于提高跟踪性能问题,文献[8]研究了集中式MIMO雷达在同时多波束工作模式下的资源分配问题,并证明了通过优化分配发射波束和功率可有效提高目标跟踪精度。文献[9]通过推导后验克拉默-拉奥下界(Posterior Cramer-Rao Lower Bound,PCRLB),提出了一种集中式MIMO雷达同时多波束模式下的功率-带宽联合分配算法。文献[10]推导了理想检测条件下的预测条件克拉默-拉奥下界(Predicted Conditional CRLB,PC-CRLB),并研究了分布式雷达网络中的节点选择-功率分配问题。在文献[8,9]的基础上,文献[11]进一步研究了集中式MIMO雷达多目标跟踪中的功率-带宽-波束联合分配问题。文献[12,13]对杂波环境下的跟踪性能下界进行推导,并研究了多雷达系统中的功率分配问题以及子阵选择-功率联合分配问题。为进一步提高多目标跟踪场景下的跟踪质量,文献[14]基于服务质量(Quality of Service,QoS)准则,提出了一种波束-功率联合分配算法,以使各目标的跟踪误差逐渐逼近期望值。为提升满足跟踪精度要求的目标数量,文献[15]提出了一种基于目标容量的同时多波束功率分配算法。文献[16]考虑使目标跟踪精度和满足精度要求的目标容量同时最大化,研究了压制式干扰场景下的波束选择-功率分配问题。在减少发射资源消耗方面,文献[17]提出一种面向射频隐身的发射节点-驻留时间-功率联合分配算法,该算法在满足跟踪精度要求的前提下尽可能减少对组网雷达系统的射频资源消耗。针对机载组网雷达单目标跟踪场景,文献[18]提出一种基于低截获概率(Low Probability of Intercept,LPI)性能准则的资源分配算法。文献[19]针对集中式MIMO雷达多目标跟踪问题,提出一种基于QoS准则的稳健功率分配算法。文献[20]建立了集中式MIMO雷达体制下的空-时资源分配和波形选择优化模型,在保证目标有效检测的前提下,对系统资源消耗量和跟踪性能同时进行优化。针对机会约束规划的机会阵雷达网络系统,文献[21]研究了单批机动目标跟踪下的发射功率最小化问题。文献[22]同时考虑目标跟踪精度和低截获概率(LPI),提出一种相控阵雷达网络多目标跟踪中的目标指派和资源联合分配算法。文献[23]进一步提出一种基于LPI的功率-驻留时间-带宽-脉冲长度多参数联合分配算法。
上述工作为MIMO雷达资源分配问题的研究打下了良好基础,但仍存在一些不足之处。如当前对于机动目标跟踪的资源分配研究成果较少,且针对不同运动特性和电磁特性目标的威胁度评估问题缺乏应有的关注。此外,对于多目标跟踪中同时考虑跟踪精度和低截获性能的资源分配研究成果也十分有限。基于上述情况,本文针对集中式MIMO雷达多机动目标跟踪场景,提出了一种低截获背景下的快速功率分配算法。本算法基于同时多波束工作模式,如图1所示,雷达同时发射多个宽波束对空间进行监视,并在接收机中形成窄波束以提取目标信息。此时,每个目标都被一个波束独立进行跟踪,通过合理地向各发射波束分配功率,可提高资源利用率和雷达跟踪性能。

图1 集中式MIMO雷达同时多波束工作模式Fig.1 Simultaneous multi-beam working mode of the collocated MIMO radar
具体而言,本文首先将目标运动模型构建为自适应当前统计(Adaptive Current Statistical,ACS)模型。然后推导了PC-CRLB,并将其作为跟踪性能下界。针对各目标运动特性和电磁特性的差别,构建了目标威胁评估模型。其次,分别计算了基于PC-CRLB的目标跟踪误差评估指数和雷达截获概率,并通过引入线性化机制构建了关于发射功率的优化模型。最后,针对优化模型的凸性质和单调性,采用了一种低复杂度的基于序列松弛的求解算法进行快速求解。仿真结果验证了所提算法的可行性和时效性。本文构建的基于发射功率分配的认知跟踪系统如图2所示。

图2 认知跟踪系统示意图Fig.2 Schematic diagram of cognitive tracking system
2 系统建模
假设某集中式MIMO雷达位于x-y平面内,雷达采取均匀线阵排布,阵元数为M×N。将第m个发射阵元和第n个接收阵元分别表示为Tm和Rn,其中∀m∈{1,2,...,M},∀n∈{1,2,...,N},且对应阵元间距分别为dt和dr,雷达阵列模型如图3所示。

图3 集中式MIMO雷达阵列模型Fig.3 Collocated MIMO radar array model
为简化模型,给出如下假设:
(1) 系统采用同时多波束工作模式,各发射阵元发射窄带正交信号;
(2) 已知目标空域内存在Q个运动目标,各目标初始位置为先验信息;
(3) 考虑远场条件,认为目标散射系数对各发射、接收阵元相同;
(4) 为稳定系统内部各器件工作负荷,将各发射波束的功率平均分配给对应发射阵元。
2.1 信号模型
假设在k时刻,该集中式MIMO雷达向第q个目标发射的波形为
其中,Pk,q为发射功率;Ek,q(t)为归一化的发射信号复包络;fc为载波频率。该信号的有效带宽βk,q和有效时宽Tk,q分别满足
以及
经目标反射后,接收信号可表示为
其中,ak,q为目标q的反射复增益;γk,q为信号衰减系数,与径向距离的4次方成反比;τk,q为信号时延;为信号多普勒频移;nk,q(t)为零均值的复高斯白噪声。
2.2 运动模型
当前用于描述目标机动特性的运动模型主要分为单模型和多模型两类[24]。由于单模型算法无须建立复杂的模型集来匹配目标机动,因此更具时效性。当前统计(Current statistical,CS)模型是一种比较切合实际的单模型,通过构建非零均值的加速度模型能较全面地描述目标机动特性[25],但存在自适应性不足的问题,需要进行改进。通过将Jerk输入估计引入CS模型中,结合改进的输入估计方法[26],对CS模型中状态方程和机动加速度方差的调整方法进行改进,从而建立起ACS模型。将目标反射的复增益建模为一阶马尔可夫过程,构建扩展目标状态向量,对应的增广矩阵状态方程可表示为
2.3 观测模型
利用ESPRIT算法[29]对接收信号进行处理,可从中提取k时刻目标相对雷达的径向距离、多普勒频率、方位角以及反射增益等估计信息。对应的等效非线性量测模型为
其中,Rk,q,fk,q和θk,q分别代表目标q相对雷达工作中心的径向距离、多普勒频率和方位角;(x0,y0)代表雷达工作中心位置;λ表示雷达的工作波长;arctan 2(·)表示4 象限反正切函数;代表一个1×i维的向量,其中除第j个元素为1外其余元素均为0;ϖk,q~N(0,Gk,q)为零均值高斯白噪声,其协方差矩阵可表示为
其中,矩阵对角线元素分别对应于式(10)中所有量测值的量测误差协方差,且满足[8]
其中,Bw为半功率波束宽度。由式(12)可知,观测信息中所有参数的误差协方差均与发射功率Pk,q成反比。因此,量测误差协方差矩阵可以重新表示为
由式(13)可知,通过提高发射功率,能够提高雷达量测精度。当存在多批目标时,需要对有限的发射功率进行合理分配。特别地,当雷达系统在作战环境中执行多目标跟踪任务时,其功率分配策略的制定应充分考虑各目标威胁程度的差异。因此,需要建立合理的目标威胁评估机制来指导优化模型建立。
3 跟踪性能量化
3.1 PC-CRLB推导
标准PCRLB[9]可为无偏估计提供一个下界,并且已经被证明在高信噪比情况下非常接近实际跟踪误差[14]。然而,由于标准PCRLB基于以往所有时刻的观测信息对目标状态进行估计,因此并不适用于观测信息变化剧烈的机动目标跟踪场景[13]。为了更好地利用观测信息,并结合机动跟踪的非线性特点,采用粒子滤波对目标状态进行估计,并且推导基于粒子滤波的PC-CRLB。首先,PC-CRLB满足如下不等式[10]:
其中,JP(xk,q|z1:k-1,q)和JZ(xk,q|z1:k-1,q)分别为先验信息的PC-BIM矩阵和数据信息的PC-BIM矩阵。为避免式(16)中复杂的数学期望运算,结合粒子滤波机制,PC-BIM可近似计算为[31]
以往跟踪性能驱动的资源分配文献可具体分为:最大化最差目标的跟踪精度[10]和最大化目标整体跟踪精度两种类型[12]。然而在实际应用,各目标的威胁度并不相同,因此简单地对各目标的PC-CRLB进行求和或寻找其最大值,并将其作为目标函数不够合理。3.2节将针对目标运动特性和电磁特性,构建威胁度评估模型。
3.2 目标威胁评估模型
随着航空兵器的发展,空袭样式逐渐多样、目标运动特征变化逐渐加剧,导致地面防空雷达面临的战场环境复杂多变[34]。构建准确及时的目标威胁评估模型,可有效提升地面防空雷达系统的资源分配效能,增强抗机动突防能力。
针对目标威胁评估,主要考虑以下4个方面:径向距离、径向速度、目标航向、电磁散射特性。具体而言,目标威胁度的量化过程如下:
(1) 径向距离
(2) 径向速度
(3) 目标航向
(4) 电磁散射特性
至此,目标q在k时刻的威胁度可建模为
其中,ηj(j=1,2,3,4)为径向距离、径向速度、目标航向和隐身性能的权重系数,满足η1+η2+η3+η4=1。对χk,q进行归一化后,可得
4 低截获背景下的功率分配算法
4.1 截获概率模型
假设目标携带拦截接收器,当接收器检测到雷达信号的概率大于其阈值时,可能对地面雷达生存造成威胁,因此需要减小目标的截获概率。为简化模型,假设所有目标携带拦截接收器相同且工作在同种模式。由文献[23]可知,目标q在k时刻对雷达发射信号的截获概率为
其中,pfa为拦截接收器的虚警概率;Gt为雷达发射天线增益;GI为拦截接收器的接收天线增益;GIP为拦截接收器的信号处理增益;k0代表玻尔兹曼常数;T0代表雷达接收机的噪声温度;BI为拦截接收器的带宽;FI为拦截接收器的噪声因子;erfc(x)函数展开为
4.2 功率优化模型
由上述分析可知,MIMO雷达对目标的功率分配与跟踪精度和截获概率均密切相关。一般而言,为了保证低截获性能,要求系统降低发射功率,而为了实现高精度跟踪,应提高发射功率。在防空作战时,精确跟踪能力和低截获能力都是雷达系统的追求目标;并且,随着战场态势的实时变化,对跟踪能力和低截获能力的要求也发生改变。为建立关于目标跟踪精度和雷达低截获概率的优化模型,我们引入了线性约束机制[36]。考虑到雷达发射功率越高,跟踪误差越低[15]、截获概率越高[37],因此,为平衡二者的单调性差别,令
其中,F2(Pk,q)表示雷达未被目标q截获的概率。
综上,优化模型可描述如下:
4.3 求解方法
式(28)的约束条件均是线性的,因此其性质由目标函数决定。在式(28)中,目标威胁值主要由目标运动状态和电磁特性决定,在固定时刻可以近似看作常数。类似地,任务重要性权值和在固定时刻也可以看作常数。而F1(Pk,q)和 F2(Pk,q)均是关Pk,q的凸函数[38],因此,式(28)是一个关于发射功率的凸优化问题,通过采用内点法[17]便可轻松求解,但其算法复杂度为O(Q3.5)[39]。为提高时效性,基于目标函数关于功率的单调性特征和minmax问题[40]的特点,本节给出一种算法复杂度仅为O(Q)的快速求解方法。算法描述如下:
引理1:Dk,opt≥Dk。
引理2:若Dk≤,∀q=1,2,...,Q。则Dk,opt=Dk,此时与之对应的解Pk,q=是最优的。
引理3:若Dk>,∀q=1,2,...,Q。则最优解Pk,opt中的第q个元素的值为Pk,q,opt=。
引理1—引理3的证明过程见附录。结合上述3个引理,式(28)可以通过反复求解式(29)并且直接令Pk,q,opt=得到,流程见表1。

表1 功率快速求解算法Tab.1 Fast power solving algorithm
5 仿真结果及分析
5.1 基本参数设置
本节仿真设置如下:考虑单部集中式MIMO雷达同时跟踪Q=3个目标的场景。假设在x-y平面中,雷达工作中心位于原点处。采用粒子滤波算法对目标状态进行实时估计,粒子数量为Np=200。设置蒙特卡罗试验次数为Nsim=100,共有30帧数据用于每次试验。雷达和拦截接收器的相关参数设置情况见表2,各目标初始运动参数如表3所示,目标与雷达的几何位置如图4所示。假设用发射功率为 0.4Ptotal的雷达波束对距离50 km外RCS为1的目标进行照射时,相应的接收端观测误差为G0=diag(1002,102,0.12,22,22)。在ACS模型中,设置各目标的初始机动频率为u0=0.06,各目标在x方向和y方向的加速度变化如图5所示。

表2 仿真参数设置Tab.2 Simulation parameter setting

表3 初始时刻目标运动参数Tab.3 Initial target motion parameters

图4 雷达与目标的空间位置关系Fig.4 Spatial position relationship between radar and target

图5 各机动目标的加速度变化情况Fig.5 Acceleration variation of each maneuvering target
5.2 任务场景构建
为探究参数变化对功率分配结果的影响以及验证模型的鲁棒性,设置了目标RCS起伏模型,具体如图6所示。

图6 目标RCS起伏模型Fig.6 Target RCS fluctuation model
根据仿真条件,运用层次分析法来确定目标威胁度模型中各目标特性对应的权重值,最终计算得到整个跟踪任务期中各目标威胁值如图7所示。此外,为验证优化模型的正确性,考虑两种任务重要性权值模型,具体如下:

图7 目标威胁权重模型Fig.7 Task threat weight model
(1) 常数任务重要性权值模型ℓ1。在该模型下,雷达对所有目标的跟踪性能和低截获性能重要性权值恒定不变,且满足=0.8,=0.2,∀q=1,2,3,∀k=1,2,...,30。在这种情况下,资源分配的主要方向是提高跟踪精度。
(2) 时变任务重要性权值模型ℓ2。在此模型中,雷达对各目标所赋跟踪性能和低截获性能重要性权值各不相同,且各目标对应权值随时间发生变化,的所有取值如图8所示。因此,雷达对各目标的任务执行要求实时改变。

图8 ℓ2模型中的任务重要性权值Fig.8 Task importance weight in model ℓ2
5.3 算法性能检验
图9和图10分别给出了ℓ1模型和ℓ2模型下的目标的真实轨迹及其估计轨迹。结合图8可知,对目标1而言,在ℓ2模型中,从第16 s开始跟踪精度重要性权值降到小于0.4,而低截获能力重要性权值上升到大于0.6,因此,在ℓ2模型中对目标1的跟踪效果将弱于在ℓ1模型中的跟踪效果,这一点在图9和图10的跟踪轨迹中可以看出。此外,对于目标2而言,随着径向距离越来越远,跟踪误差也逐渐增大。在ℓ1模型中,由于更多关注目标跟踪精度,雷达对目标2的跟踪效果较为理想。但在ℓ2模型中,尽管在第15 s之后关于目标2的跟踪精度重要性权值上升到了0.6,但仍然比在ℓ1模型中的跟踪效果更差。由于在第15 s之后,目标3的跟踪精度重要性为所有目标中最高,且达到了ℓ1模型中的权值,因此必然导致更多的功率资源将分配给目标3,进而使其跟踪效果比在ℓ1模型中更好。
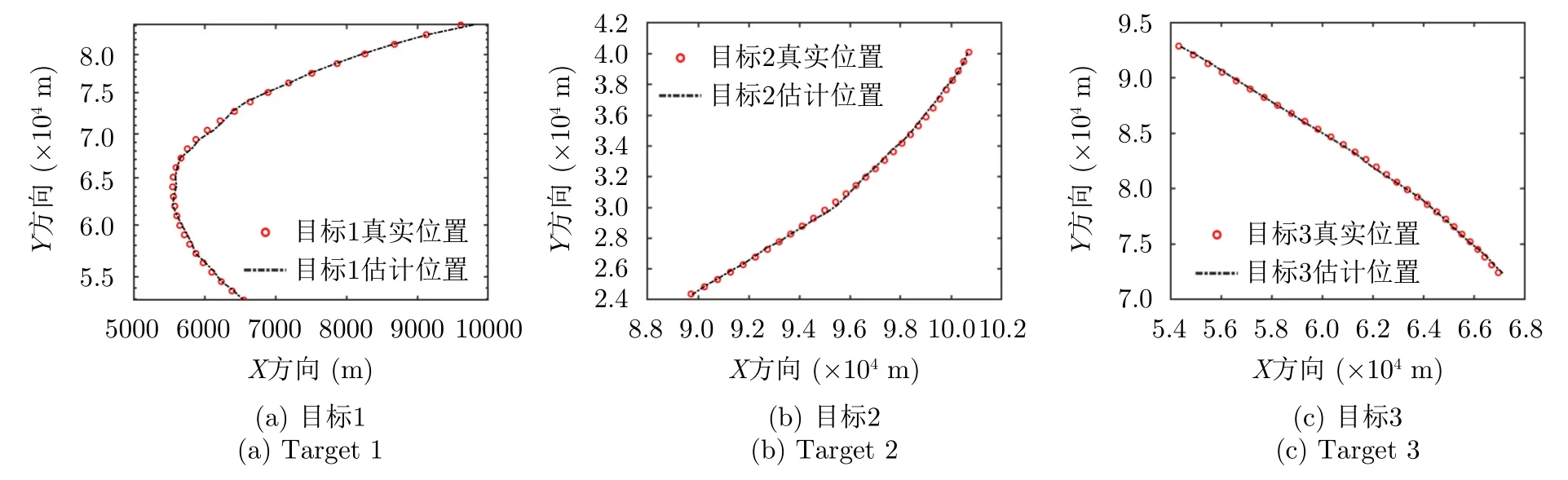
图9 ℓ1模型下的目标跟踪轨迹Fig.9 Target tracking trajectory in model ℓ1

图10 ℓ2模型下的目标跟踪轨迹Fig.10 Target tracking trajectory in model ℓ2
值得注意的是,在两种模型下,雷达均能较好地完成对所有目标的跟踪任务。为进一步描述目标跟踪精度,定义跟踪效果最差目标的均方根误差(Root Mean Square Error,RMSE)为
图11和图12分别给出了在本文所提算法(任务模型1和任务模型2)、min-max PC-CRLB功率分配算法和功率平均分配3种资源分配策略下计算得到的跟踪效果最差目标对应的PC-CRLB和RMSE。其中,min-max PC-CRLB功率优化分配算法表示的优化模型如下:

图11 各算法关于最差情况的PC-CRLB性能对比Fig.11 PC-CRLB performance comparison of each algorithm on the worst case

图12 各算法关于最差情况的RMSE性能对比Fig.12 RMSE performance comparison of each algorithm on the worst case
在min-max PC-CRLB功率分配算法中,雷达仅需要尽可能地提高最差目标的跟踪精度,并采用内点法对式(32)进行求解。由图11和图12可知,功率平均分配策略在所有算法中表现最差,并且不能满足跟踪误差阈值要求。min-max PC-CRLB功率分配算法由于仅需考虑跟踪精度,从跟踪性能角度而言,在所有算法中表现最佳。所提算法同时考虑了目标跟踪性能和雷达低截获能力,因此,在跟踪性能方面表现稍差于min-max PC-CRLB功率分配算法。此外,由于任务模型1更加关注跟踪性能,因此,所提算法在任务模型1下的跟踪性能优于任务模型2下的跟踪性能。
图13展示了不同资源分配策略下关于雷达信号的最大截获概率性能对比。由结果可知,在功率平均分配机制下,随着目标1距离雷达越来越近,其对雷达信号的截获概率逐渐增加,最终达到1。由于min-max PC-CRLB功率分配算法仅考虑跟踪性能,未对抗截获能力进行优化,min-max PC-CRLB功率分配策略下的最大截获概率在3种功率优化分配算法中表现最差,且在初始时刻概率值接近1。而相较任务模型1而言,任务模型2更加关注雷达的抗截获能力,因此,任务模型2下所提算法的最大截获概率在所有算法中最低。
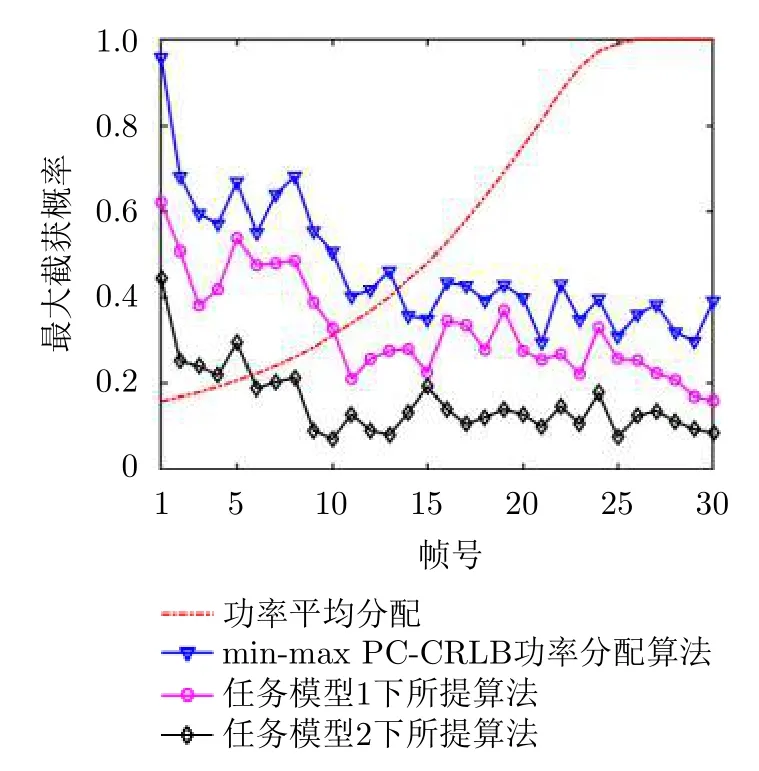
图13 各算法关于最大截获概率的性能对比Fig.13 Performance comparison of each algorithm for maximum intercept probability
图14和图15分别给出了在ℓ1模型和ℓ2模型下采用本文所提算法得到的功率分配结果。图中不同网格的颜色代表归一化的功率分配比率,定义为=Pk,q/Ptotal。为更好地分析功率分配结果,图16给出了各目标与雷达的实时距离。

图14 ℓ1模型中的雷达功率分配结果Fig.14 Results of radar power allocation in model ℓ1
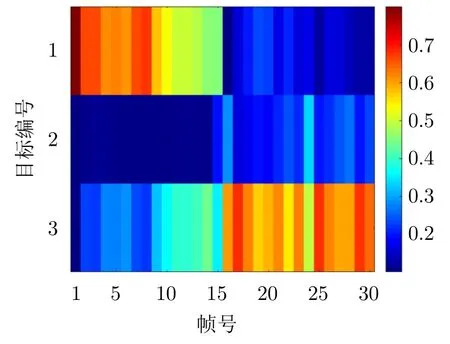
图15 ℓ2模型中的雷达功率分配结果Fig.15 Results of radar power allocation in model ℓ2

图16 各目标相对雷达的径向距离Fig.16 Radial distance of each target relative to radar
首先,对图14的功率分配结果进行分析。在ℓ1模型下,雷达主要考虑各目标的跟踪性能。根据式(12)可知,距离越远、RCS越小的目标对应的量测误差越大,其跟踪误差也会相应增大。结合图7、图14、图16可知,由于目标1始终距离雷达最近,理论上能够实现较好的跟踪精度,在min-max优化框架下相应的分配资源应较少[11]。但由于其目标威胁度较高,因此目标1获得功率资源较多。但随着径向距离的拉大,目标1所获功率资源呈现阶梯式的下降特征。此外,由于目标2的目标威胁度大于目标3,且目标2的径向距离逐渐增加,直至成为3个目标中距离雷达最远目标,使得跟踪精度变差,因此,目标2所获得的功率分配资源较多,并且随时间增加呈现一定的上升特征。尽管目标3距离雷达较远,但由于其威胁程度最小,并且RCS值最大,使其实际跟踪精度较好地满足预期跟踪精度要求,因此,目标3所获功率资源最少。
由图8、图14和图15可知,相较于在ℓ1模型下的功率分配结果,由于目标1在ℓ2模型中第15 s之后跟踪性能重要性权值下降到低于0.4,导致目标1在15 s之后功率分配值的阶梯式下降特征更加明显。结合图8可知,由于目标2在跟踪周期的前半段跟踪精度重要性权值为0.4,为所有目标中最低,因此,目标2在第15 s之前分配得到的功率值最低。由于在ℓ2模型下第15 s后目标3的跟踪精度重要性权值上升到0.8,因此,在第15 s后目标3成为各目标中跟踪精度重要性权值最高的目标。相应地,如图15所示目标3从16 s开始分配得到最多的功率资源。
为验证所提求解算法的时效性,在一台搭载i7-10750h处理器、16 GB双通道内存的计算机上,采用MATLAB R2020b软件对算法求解时间进行计算。经过100次蒙特卡罗试验取平均值后得到算法平均计算时间如图17。通过和内点法进行比较,可知所提算法具有更高的时效性,可使平均计算时间降低近50%。

图17 算法平均计算时间Fig.17 Average calculation time of algorithm
6 结语
本文基于集中式MIMO雷达系统,提出了一种低截获背景下针对多机动目标跟踪的快速功率分配算法。该算法构建了目标综合威胁度模型,并在此基础上建立了关于机动目标跟踪误差和雷达低截获性能的加权目标函数。通过在给定发射功率预算条件下动态调整各发射波束的功率大小,以实现提高目标跟踪精度的同时保证雷达具备低截获能力。为提高模型求解时效性,采用了一种基于序列松弛的凸优化算法进行求解。
仿真结果表明:(1)相比于功率平均分配策略和以提高跟踪精度为目标的功率分配策略相比,所提算法能够在提高目标跟踪精度的基础上保证雷达具备低截获能力;(2)在任务模型为常数模型和时变模型两种情况下,所提算法均能实现较好的跟踪性能和低截获性能。因此所提算法可通过调节任务重要性权值的方式,实现在一定可调节范围内提高目标跟踪精度和低截获性能,从而具有良好的任务设计自由度和鲁棒性;(3)本文采用的基于序列松弛的快速求解方法比内点法求解速度提高近50%。由于本文仅考虑发射功率分配情形,接下来将考虑对信号带宽和发射波形等参数进行联合优化分配,以进一步提高多目标跟踪性能。
附录
(1) 引理1证明:
根据非线性优化理论[41],由于Dk是式(32)的最优解,而式(29)又是式(28)的松弛形式。因此引理1显然成立。
(2) 引理2证明:
(3) 引理3证明:
