频谱共存下面向多目标跟踪的组网雷达功率时间联合优化算法

时晨光 董 璟 周建江

(南京航空航天大学雷达成像与微波光子技术教育部重点实验室 南京 210016)

1 引言

当前，空战逐渐由信息化向智能化过渡，通过多雷达协同能够提高空天目标的预警探测能力与情报保障能力，特别是能够提高复杂战场条件下对非合作特种军用目标的连续探测跟踪能力，已成为国内外研究人员的共识。与此同时，随着军事装备技术的飞速发展，多雷达协同的作战环境也变得越来越复杂，电磁频谱环境的复杂性、时变性以及难以预测性，对雷达系统提出了严峻挑战。如何让雷达系统在与通信基站共享同一工作频段的条件下，通过优化自身的射频辐射资源配置以提升其探测跟踪性能，已经成为一个热点问题[1–7]。

对于共享频谱的雷达和通信系统，需要设计有效的管理方案来减少两者间的相互干扰，从而保证彼此都能正常工作[8–18]。针对该问题，Zheng等人[9]提出了一种非合作雷达/通信共存的自适应干扰消除方法，优先考虑保护通信系统性能，并通过求解凸问题对雷达参数和通信解调误差进行估计，仿真结果验证了算法的有效性与优越性。鲁彦希[10]以雷达对通信系统的干扰能量为约束条件，对组网雷达节点选择与功率参数进行自适应优化设计。文献[11]提出了用于多雷达系统中多目标跟踪的通信感知资源调度策略，考虑在最小化雷达对通信干扰的同时，对雷达发射功率和采样间隔进行优化分配，仿真结果表明，该算法能够有效提高系统多目标跟踪性能。文献[12]针对异构雷达与通信系统之间的频谱共存问题，通过分配有限的发射功率、驻留时间和共享带宽资源，来提高组网雷达的跟踪性能，同时保持通信下行链路的吞吐量水平。文献[13]对通信系统传输协方差矩阵以及基于稀疏感知和矩阵补全的多输入多输出(Multi-Input Multi-Output,MIMO)雷达采样方案进行联合设计，旨在保持通信系统的平均容量和发射功率的同时，最大限度地降低雷达接收机处的有效干扰功率。Hessar等人[14]采用具有低复杂度的空频域隔离机制，并结合具体的雷达通信系统操作策略解决频谱共存问题。韩凯峰等人[15]提出了一种雷达通信频谱共存场景下基于块对角化的通信雷达波束设计方案，该方案以通信对雷达无干扰及通信用户间无干扰为约束，在满足功率资源约束的条件下，最大化通信系统和速率。仿真结果表明，所提算法适用于多种场景，且与现有算法相比，具有更低的计算复杂度和更好的通信性能。文献[16]针对多雷达通信一体化系统相互干扰的问题，提出了基于正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)子载波分配的雷达通信一体化系统，利用子载波间的互相正交性，消除雷达与通信用户间干扰以及通信用户之间的相互干扰。文献[17]提出了频谱共存下基于Stackelberg博弈的多基地分布式雷达功率分配算法，在满足预先设定的目标探测信干噪比阈值的情况下，最小化各雷达辐射功率，从而起到保护通信基站不受雷达射频辐射干扰。

组网雷达具有多雷达探测资源协同运用与信息融合紧密结合的技术体制特点，且在目标检测、跟踪、识别等诸多场景中均具有显著优势[19]。射频资源管理是组网雷达目标跟踪任务中重要的一环，通过对辐射功率、驻留时间、信号带宽和辐射采样间隔等射频参数进行优化，能够有效提升雷达系统性能[20–35]。Zhang等人[20]对杂波环境下分布式MIMO雷达多目标跟踪的资源分配问题进行了研究，通过对雷达节点和功率资源进行自适应优化配置，最小化多目标跟踪误差，并提出了次优解排序方法对该优化模型进行求解。Lu等人[21]提出了一种机载雷达路径规划与辐射资源联合优化算法，该算法将机载雷达路径规划和辐射资源作为优化参数，并采用多目标跟踪误差效用函数作为优化目标，采用多步分解法和梯度投影法对该问题进行求解，仿真结果表明，该算法有效提升了雷达系统多目标跟踪性能。文献[22]提出了面向低截获概率的机载雷达功率资源分配算法，该算法以包含雷达多目标跟踪误差和截获概率的加权为目标函数，并采用两步分解法对模型进行求解。仿真结果表明，该算法能够有效降低跟踪过程中雷达被敌方无源探测系统截获的概率。文献[23]提出了一种多目标跟踪场景下的相控阵雷达最优资源分配算法，该算法以多目标跟踪性能作为约束条件，以最小化雷达资源消耗为优化目标，对雷达的功率和带宽参数进行联合优化分配。Cheng等人[24]提出了同时多波束集中式MIMO雷达自适应时空资源与波形联合优化算法，该算法采用智能优化方法对雷达采样周期、发射能量、子阵列数和多波束方向矢量等多个参数进行联合优化设计，能够自适应选择工作模式，从而在最大化目标跟踪精度的同时，达到最小化雷达资源消耗的目的。文献[25]以最小化雷达驻留时间和辐射功率资源加权和为优化目标，结合内点法和匈牙利算法对雷达节点分配方式、辐射功率和驻留时间进行优化，仿真结果表明，相较于资源均匀分配算法，该算法能够有效提升雷达系统的射频隐身性能。文献[26]对多基地雷达之间的博弈优化模型进行分析，将预先设定的信干噪比阈值作为约束条件，结合凸优化方法和博弈思想，对多基地雷达功率分配和波束形成进行联合优化，仿真结果验证了该算法对雷达间的干扰抑制能力。文献[27]提出了基于Stackelberg博弈的组网雷达功率分配算法，该算法旨在最小化功率消耗的同时最优化目标跟踪精度，仿真结果表明，该算法能够有效提高雷达系统的资源利用率。严俊坤等人[28]提出了基于机会约束的集中式MIMO雷达功率分配算法，该算法以MIMO雷达高概率满足多目标跟踪精度为约束条件，以最小化MIMO雷达的发射功率为优化目标，并采用凸优化方法对优化模型进行求解。文献[29]提出了分布式MIMO雷达多目标跟踪接收波束资源分配算法，该算法能够基于跟踪周期中的反馈信息，采用内点法实现接收波束与目标之间的最优分配。

综上所述，上述研究成果为优化组网雷达目标跟踪性能和解决雷达通信频谱共存问题奠定了坚实的基础。然而，针对多目标跟踪场景，文献[10,11]等已有研究并未充分考虑雷达通信频谱共存环境下组网雷达功率时间资源的联合优化配置，解决该问题对于提升我方雷达探测系统的目标跟踪精度、射频资源利用率及对敌作战效能具有重要意义。因此，本文围绕多目标跟踪场景下雷达通信频谱共存和组网雷达辐射资源管理领域，研究了频谱共存下面向多目标跟踪的组网雷达射频资源联合优化分配问题。首先，由于各优化参数的约束不同，采用发射能量作为优化参数的算法复杂度较高，因此针对频谱共存环境下多目标跟踪问题，建立了组网雷达功率时间资源联合优化模型，以最小化多目标跟踪贝叶斯克拉默-拉奥下界(Bayesian Cramér-Rao Lower Bound,BCRLB)为优化目标，以给定的组网雷达射频资源和预先设定的通信基站最大可容忍干扰能量阈值为约束条件，通过联合优化雷达节点选择、发射功率和驻留时间等射频辐射参数，提升组网雷达的多目标跟踪精度。仿真结果验证了本文所提算法的可行性和稳健性。

2 系统模型

考虑一个由N部雷达组成的组网雷达系统，各雷达节点分散部署于二维直角坐标系中，并保持时间、空间、频率同步。第n部雷达的位置坐标可以表示为xR,n=(xR,n,yR,n),n=1,2,...,N。另外，假设组网雷达系统的探测范围内存在Q个运动目标和C个通信基站。

2.1 目标运动模型

式中，rq表示过程噪声强度。

2.2 雷达量测模型

2.3 干扰模型

通信基站在一定频带范围内持续性向外辐射电磁信号，会使雷达系统的探测跟踪性能下降。另外，在频谱共存环境下，雷达在执行目标探测跟踪任务时也会对通信基站的正常工作造成负面影响。因此，本节对雷达和通信基站两者的相互干扰进行分析。首先，考虑通信基站对雷达的干扰，此类干扰可以看作多种随机调制信号的组合。根据中心极限定理，假设信号形式可近似表示为占据一定带宽的循环对称带限的复高斯序列，该信号的功率谱密度(Power Spectral Density,PSD)在雷达的工作通带范围内表现出了均匀特性[36]，即

式中，Nm,n表示信号PSD强度；fU,m,n和fL,m,n分别表示第m个通信基站和第n部雷达共同覆盖频带的上界和下界。定义第m个通信基站对第n部雷达产生的干扰信号的时域协方差矩阵Ξm,n可以表示为[10]

式中，Ξm,n的第u行第v列的元素为对应信号延时的自相关函数，同时也是通信基站信号PSD的离散时间傅里叶逆变换；Ts表示信号采样周期。考虑到距离衰减等因素影响，第m个通信基站对第n部雷达施加的干扰噪声为

式中，χm,n表示传输信道的强度系数；表示第m个通信基站在第n部雷达频带范围产生的干扰序列；表示通信基站m相对于雷达n的方位角。假设各通信基站的发射信号相互正交，则所有通信基站对雷达n的干扰时域协方差矩阵可以表示为

式中，xC,m表示第m个通信基站的位置。由式(8)可知，(fU,m,n-fL,m,n)值越大，则通信基站对雷达的干扰能量越强；如果第m个通信基站和第n部雷达在频谱上没有覆盖，则fU,m,n-fL,m,n=0，即可认为对应的干扰强度为0。

雷达在跟踪运动目标时对通信基站的干扰是时变的，且与目标的运动状态有关。本文使用雷达发射信号能量的联合空频域分布来表征干扰强度，可以计算为

式中，sn=[sn(1),sn(2),...,sn(L)]T表示具有有限间隔的雷达波形序列；表示雷达发射信号能量的空间分布[10]，即

3 频谱共存下面向多目标跟踪的组网雷达功率时间联合优化算法

针对频谱共存环境下多目标跟踪资源分配问题，提出一种面向多目标跟踪的组网雷达功率时间联合优化分配算法，旨在满足给定雷达系统射频资源和预先设定的通信基站最大可容忍干扰能量阈值等约束的条件下，对雷达节点选择、发射功率和驻留时间等射频参数进行自适应优化配置，从而在保证通信基站正常工作的同时，有效提升组网雷达的多目标跟踪精度。

3.1 优化模型建立

在建立优化模型之前，需要推导表征目标跟踪精度衡量指标的解析表达式。文献[37]中指出，在参数无偏估计的条件下，BCRLB为运动目标跟踪的均方误差提供了下界，可以用来表征组网雷达跟踪运动目标的性能衡量指标。首先，推导出k时刻目标q的预测贝叶斯信息矩阵表达式为

本文提出了一种频谱共存下面向多目标跟踪的组网雷达功率时间联合优化算法，通过联合优化分配雷达节点选择、发射功率和驻留时间等射频辐射参数，在满足给定的雷达射频资源和预先设定的通信基站最大可容忍干扰能量阈值的条件下，最大限度地降低组网雷达系统的多目标跟踪误差，可构建如下数学优化模型：

式中，Tmax和Tmin分别表示各雷达驻留时间的上界和下界；Pmax和Pmin分别表示各雷达发射功率的上界和下界；Ttotal和Ptotal分别表示照射各目标的所有雷达驻留时间和发射功率之和；Emax表示通信基站所能容忍的最大雷达干扰能量阈值；表示k时刻每部雷达最多可跟踪一个目标；∂max表示各时刻组网雷达跟踪目标q可选择的最多雷达节点数目。

3.2 优化模型求解

同样地，设定发射功率和驻留时间两个参数的优先级相同，采用SDP算法对优化模型(19)进行求解，得到所选择雷达节点的发射功率和驻留时间分配值，进而可以得到(∂max-1)个射频资源配置方案及其对应的多目标跟踪误差。

步骤3 选取步骤2所有方案中最小的多目标跟踪误差与其对应的射频资源优化分配方案作为备选方案，并将该资源优化分配结果作为下一次循环的初始值。跳转至步骤1，直到连续两次得到的备选方案多目标跟踪误差差值小于某一设定的阈值时，跳出循环，并将得到的优化分配方案作为k时刻跟踪目标q的最优雷达节点选择方案和功率时间优化分配方案。

步骤4 确定下一个跟踪的目标，移除步骤3已选取的雷达节点，跳转至步骤1，直到对所有目标的跟踪方案都完成优化，即可得到k时刻组网雷达跟踪多目标时的雷达节点选择方案和功率时间联合优化分配方案。上述算法流程如算法1所示。

4 仿真结果及分析

为了验证频谱共存下面向多目标跟踪的组网雷达功率时间联合优化算法的可行性与有效性，本节进行了如下仿真：假设组网雷达系统由N=6部位置固定且已知的雷达组成，各部雷达的系统参数均相同。组网雷达系统在k时刻需要同时跟踪Q=2个目标，目标1的初始位置为[-70,0] km，以速度[900,400] m/s匀速飞行；目标2的初始位置为[70,80] km，以速度[-900,-400] m/s匀速飞行。在组网雷达探测区域中存在C=2个通信基站，如图1所示，两个通信基站位置分别为[50,50] km和[–40,50] km。雷达采样间隔为ΔT=3 s，跟踪持续过程时间为 150 s，共50帧。k时刻跟踪某一目标的雷达节点数目最大值∂max=3，通信基站最大可容忍干扰能量阈值为Emax=4.2J。其中，组网雷达仿真参数设置如表1所示。本文针对RCS不变、RCS变化和Emax阈值变化3种仿真场景分别进行仿真。

表1 仿真参数设置Tab.1 Simulation parameter settings

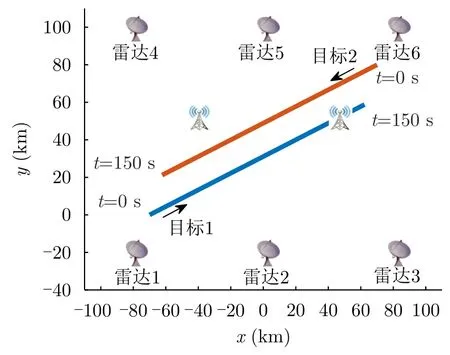
图1 组网雷达布阵及多目标运动轨迹图Fig.1 Deployment of radar networks and trajectories of multiple targets

4.1 RCS不变

在该仿真场景中，假设雷达节点观测运动目标的RCS均为1 m2，组网雷达布阵及多目标运动轨迹如图1所示。

图2给出了组网雷达跟踪目标1和目标2的节点选择和功率时间资源优化分配结果，黑色部分表示该雷达节点在相应帧未被赋予目标跟踪任务，即=0；反之，则表示该雷达节点在相应帧被赋予目标跟踪任务，即=1。从图2可以看出，组网雷达系统会优先选择距离目标较近的雷达节点进行跟踪，且各部雷达的发射功率和驻留时间分配情况均随着目标运动状态变化自适应进行调整。例如，前28帧组网雷达系统均选择了距离目标1更近的雷达1和雷达2进行跟踪，随着目标1逐渐远离雷达1而靠近雷达2，分配给雷达1的射频资源也在不断增加；对于目标2，前8帧组网雷达系统选择了距离目标2更近的雷达5和雷达6进行跟踪，并向与目标2距离变大的雷达6分配更多的射频资源。

图2 雷达节点选择与功率时间资源优化分配结果Fig.2 Radar node selection and allocation results of power and dwell time resources

同时，组网雷达系统的节点选择结果也受到通信基站最大可容忍干扰能量阈值的影响。例如，从第40帧开始，目标1与通信基站距离小，雷达对通信基站的干扰能量接近通信基站最大可容忍干扰能量阈值，导致每一帧都会选择不同的雷达节点对目标1进行跟踪。同样地，对于目标2，从第9帧开始，组网雷达系统选择对通信基站干扰较弱的雷达3替代雷达5对目标2进行跟踪。

为了进一步验证本文所提算法的优越性，将所提算法的多目标跟踪误差与其他4种对比算法进行比较。

(1) 无通信干扰算法。该算法不考虑通信基站与组网雷达之间的相互干扰，采用本文所提两步分解求解方法对组网雷达节点选择、发射功率和驻留时间等射频辐射参数进行优化配置。

(2) 随机节点选择算法。该算法对各时刻跟踪目标的雷达节点进行随机选择，并采用本文所提求解方法对选择的雷达进行发射功率和驻留时间优化配置。

(3) 均匀时间分配算法。该算法固定各雷达驻留时间，仅优化雷达节点选择和发射功率分配。

(4) 均匀功率时间分配算法。该算法固定各雷达的发射功率和驻留时间，仅优化雷达节点选择。

定义k时刻目标跟踪的平均均方根误差(Average Root Mean Square Error,ARMSE)为

式中，NMC为蒙特卡罗实验次数；为第n次蒙特卡罗实验得到的目标位置估计，本文设定NMC=100。本文所提算法和上述4种算法的ARMSE对比结果如图3所示。从图3可以看出，本文所提算法相较于有固定资源分配算法和随机节点选择算法具有更低的多目标跟踪误差，这说明雷达节点选择和射频资源优化分配对提升多目标跟踪精度有较大影响，而且优化的射频资源越多，各目标跟踪精度也越好。由于无通信干扰算法中不存在通信基站，即不考虑雷达与通信基站间的相互干扰，其所得多目标跟踪误差低于本文所提算法，这也进一步说明了通信基站的存在对组网雷达多目标跟踪性能有一定影响。总的来说，本文所提算法能够在给定组网雷达射频资源条件和预先设定的通信基站最大可容忍干扰能量阈值下，通过联合优化雷达节点选择以及辐射功率与驻留时间等射频资源配置，获得相较于其他对比算法更优的多目标跟踪精度。

图3 RCS不变场景下ARMSE对比结果Fig.3 Comparison results of ARMSE with same RCS

4.2 RCS变化

在该仿真场景中，主要研究目标RCS的变化对组网雷达射频资源配置与多目标跟踪精度的影响。目标1和目标2相对于雷达3和雷达4的RCS模型为Swerling I型，其中，各目标RCS变化情况如图4所示，目标相对于其他雷达节点的RCS值仍固定为1 m2。

图4 各目标RCS数值Fig.4 RCS values of each target

图5给出了RCS变化情况下组网雷达跟踪目标1和目标2的雷达节点选择和功率时间资源优化分配结果。从图5可以看出，由于目标回波信噪比与其RCS值呈正比关系，组网雷达系统倾向于选择相对目标RCS值较大的雷达节点来完成跟踪任务。例如，各目标相对于雷达3和雷达4的RCS值在大多数跟踪时刻均高于其他雷达，相较于RCS不变条件下的节点选择方案，由于目标1和目标2相对于雷达3和雷达4的RCS值在多数时刻均高于RCS不变场景下的RCS设定值，因此组网雷达选择雷达3和雷达4来跟踪目标1和目标2的时刻显著增多；同时，为了获得更好的目标跟踪精度，本文所提算法更多选择3部雷达对目标进行跟踪。

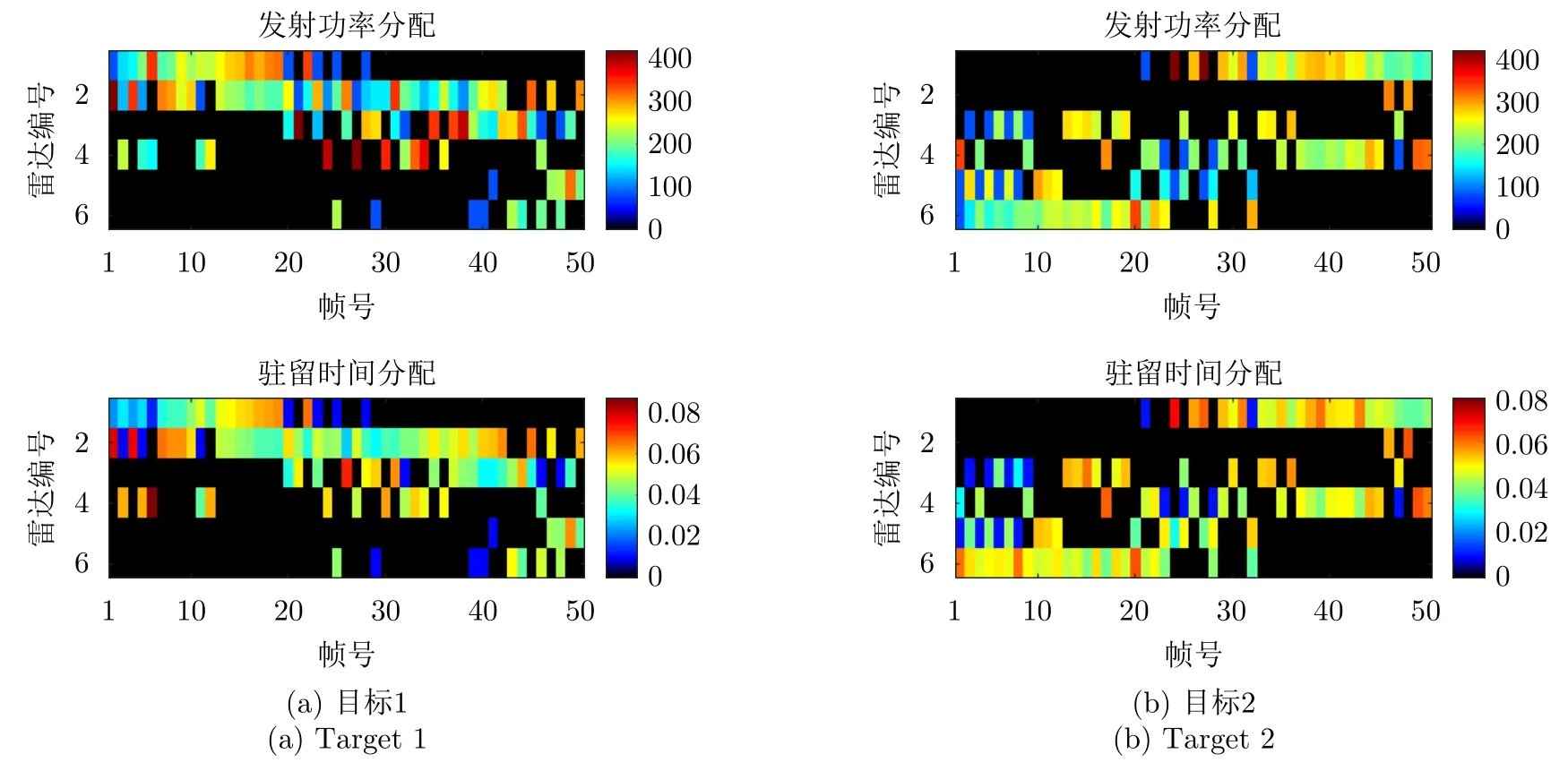
图5 RCS变化场景下雷达节点选择与功率时间资源优化分配结果Fig.5 Radar node selection and allocation results of power and dwell time resources with various RCS

同样地，RCS变化情况下本文所提算法与其他对比算法的ARMSE对比结果如图6所示。由于雷达节点选择受到目标RCS变化的影响，组网雷达的跟踪性能略差于RCS不变情况下的跟踪性能，但仍优于同一场景下的其他对比算法，体现了本文所提算法的稳健性。

图6 RCS变化场景下ARMSE对比结果Fig.6 Comparison results of ARMSE with various RCS

4.3 Emax变化

在该仿真场景中，主要研究通信基站最大可容忍干扰能量阈值，即Emax变化对组网雷达多目标跟踪精度的影响。图7给出了Emax=3 J时组网雷达跟踪目标1和目标2的节点选择和功率时间资源优化分配结果。从图7可以看出，相较于第1种仿真场景，由于Emax值变小，通信基站对雷达干扰能量的可容忍度降低，此时，组网雷达选择了满足约束条件下的最优雷达射频资源分配方案；类似地，组网雷达更多地选择3部雷达对多目标进行跟踪。

图7 Emax=3 J时雷达节点选择与功率时间资源优化分配结果Fig.7 Radar node selection and allocation results of power and dwell time resources with Emax=3 J

同样地，图8显示不同Emax条件下本文所提算法与其他4种算法的ARMSE对比结果。从图中可以看出，随着Emax值不断增加，通信基站对雷达干扰能量的可容忍度不断提升，使得可供组网雷达配置的射频辐射资源增多，于是，系统能够得到更低的多目标跟踪误差，所得ARMSE值也更逼近无通信干扰条件下的跟踪误差。

图8 不同Emax条件下ARMSE对比结果Fig.8 Comparison results of ARMSE under different Emax conditions

5 结语

本文考虑了频谱共存环境下通信基站对组网雷达多目标跟踪性能的影响，提出了一种面向多目标跟踪的组网雷达功率时间联合优化算法，以满足组网雷达射频资源和预先设定的通信基站最大可容忍干扰能量阈值为约束条件，以最小化多目标跟踪BCRLB为优化目标，通过联合优化分配雷达节点选择、发射功率和驻留时间等参数，提高了组网雷达的多目标跟踪精度。仿真结果表明，多目标跟踪精度不仅与组网雷达和各目标的空间位置关系及目标散射特性有关，而且还受通信基站最大可容忍干扰能量阈值的影响；另外，与现有算法相比，本文所提算法能够在保证通信基站正常工作的条件下，有效提升多目标跟踪性能。下一步将围绕频谱共存环境下组网雷达射频辐射参数与飞行路径联合优化问题进行研究。