Research on the distribution characteristics of explosive shock waves at different altitudes

Liang-quan Wang, De-ren Kong

Nanjing University of Science and Technology, Nanjing, 210094, China

Keywords:Shock wave overpressure calculation Pressure attenuation law Altitude correction factor Engineering numerical model

ABSTRACT

1. Introduction

With the diversification of military combat environments, the explosive environment of ammunition is not limited to plain areas;an increasing number of operations are being conducted in plateau areas [1]. The shock wave damage assessment results obtained by using the same type of ammunition in the plain environment cannot be applied to the plateau environment, and a conversion between the two cannot be carried out. This results in a small application range of a live ammunition test damage test evaluation result and low data utilization. It is not meaningful to change the selection of ammunition at altitude. Therefore, it is necessary to study the distribution characteristics of explosion shock waves under plateau or higher altitude conditions to obtain the plateau effect of explosion shock wave propagation characteristics and achieve the equivalent shock wave pressure at different altitudes.This conversion improve the application range of ammunition damage power test data[2,3].

Researchers at home and abroad have carried out research on this topic; S.D. Schleuter [4] conducted explosion experiments on hard surfaces (concrete) at various heights and obtained typical curves of explosion wave parameters in regular reflection areas with time. When an explosion source releases energy at a high altitude, the different static pressure and temperature has a significant impact on the nature of an explosive wave compared with one occurring at sea level. The proportional law of the impact of environmental conditions on an air explosion wave derived from shock wave can predict different altitude conditions.Under the test value. W.D. Kenned [5] conducted a series of experiments to measure incident pressure peaks and impulses at altitudes of 650,6,600, and 14,000 feet. These measured values were consistent with the predicted values calculated according to Sax's law. More tests have been performed in altitude simulators that reduce pressure, temperature, or both. J. Dewey and J. Sperrazza [6] conducted the first series of experiments to simulate the altitude environment. The highest altitude was 55,000 feet, and the incident pressure and impulse were measured. The ratio of the shock wave was within the allowable simulated altitude and proportional distance of the simulator. The law was thus applicable.Pang Chunqiao, Tao Gang [7] and others analyzed the shock wave data of plains and plateaus, proposed a method that could effectively predict the shock wave overpressure and positive phase impulse in plateau environments, and found that the plateau rises from a plain to 4500 m above sea level.The degree of overpressure attenuation continued to intensify with the increase in the proportional distance of the explosion. The degree of overpressure attenuation can reach more than 20%, and the attenuation of the positive phase impulse is approximately 17%. However, there is little research on the distribution and attenuation of shock waves in plateau environments,and there is no systematic detailed analysis and discussion of the peak pressure attenuation of shock waves in the existing research,so further research is needed for this aspect of research.

This paper analyzes the data of explosion shock waves in plains and plateaus, studies the distribution characteristics of plateau shock waves, and describes in detail the attenuation law of the plateau shock wave overpressure peak. To explore the differences between plain and plateau meteorological conditions, the multivariate function relationship is used. The formula fitting method analyzes and fits the existing data and obtains the plateau shock wave overpressure peak prediction functional relationship under the condition of considering multiple influencing factors. The distribution of explosive shock waves in different meteorological environments can be calculated by using this function, which provides a theoretical analysis basis for the explosive shock wave testing of ammunition in different environments.

2. Explosion shock wave measurements

2.1. Characteristics of blast shock waves

A shock wave signal is a kind of disturbance signal that propagates in a continuous medium and undergoes abrupt changes under the actions of mechanical and thermodynamic parameters such as pressure, density, and internal energy [8—11]. Shock wave characteristic parameters are used as the main reference quantity to measure the damage power of explosives or weapons.Therefore,the testing of blast shock wave characteristic parameters is very important for evaluating warhead damage power [12—14].

After a warhead is detonated, a large number of high-speed,high-pressure explosion products are produced. The explosion products spread around the spherical surface and strongly compress the near-field air of the explosion, forming an initial shock wave [15—18]. As the explosion product diffuses to the periphery, the energy of the explosion product is rapidly consumed,and the pressure quickly decays to the initial pressure of the air and continues to attenuate, even forming a negative pressure. Due to the reaction of air, the pressure rises slowly, and the cyclic compression effect reaches the explosion product. The process stops, and the pressure returns to the initial value of air pressure[19—21].Fig.1 shows an ideal case of an overpressure signal curve diagram of an explosion shock wave[22],where A is the peak point of overpressure,B is the intersection point between the signal and the initial value of air pressure,Pis the peak of overpressure,and τ＋is the positive pressure action time [23].

As seen in the above figure, an ideal shock wave signal has the characteristics of a steep rising edge,high overpressure peak,short positive pressure action time, exponential pressure decay, low negative pressure value and long recovery time.

2.2. Calculation method for explosion shock wave overpressure

At present, the commonly used shock wave overpressure calculation formulas include Henrych's formula [24] and Ye Xiaohua's modified formula[25].These two types of empirical formulas are shown in the following formulas.The formulas are obtained by nonlinear fitting based on a large amount of existing test data and combined with similar theories.

In the above formula, ΔPGis the peak overpressure of the explosion shock wave, in MPa;is the proportional distance, in m／kg1／3,whereandris the horizontal distance from the measuring point to the burst center projection point, in m.

The coefficients in the two types of functional relations are obtained by fitting under the same atmospheric pressure.To ensure the calculation accuracy,it is only suitable for the calculation of the explosion shock wave overpressure at one atmospheric pressure.Atmospheric pressure changes with altitude, and shock wave propagation through the air is closely related to atmospheric pressure.Different atmospheric pressure values will directly lead to changes in the propagation of shock waves.Therefore,to ensure the prediction accuracy of the shock wave overpressure functional relationship, it is necessary to introduce the relationship with the altitude.The height-related correction coefficient is used to correct the functional relationship and obtain the calculation formula for the explosion shock wave overpressure at different altitudes.

2.3. Test system layout plan

To study the influence of different altitudes on the distribution of warhead explosion shock waves, the experiments in this article were conducted in four different altitude environments with altitudes of 4650 m,2000 m,1500 m and 198 m.The explosion shock waves were tested at four different altitudes. The corresponding atmospheric pressures were 56.5698 kPa, 79.4811 kPa,84.5448 kPa, and 98.9672 kPa. Due to differences in the types of bombs used during the test, they were converted into TNT equivalents in the analysis. The test TNT equivalent at an altitude of 4650 m was 8 kg and 14 kg. The measuring points were arranged with the burst center as the center,and the radii were 3 m,4 m,6 m,7 m,10 m,and 15 m.Four measuring points were arranged on each radius for a total of 24 measuring points.The test TNT equivalents at an altitude of 2000 m were 2750 kg, 2400 kg, 2200 kg, 1700 kg,750 kg, 535 kg, and 128 kg, and the measuring point layout radii were 5 m,6 m,7 m,8 m,9 m,10 m,11 m,13 m,15 m,18 m,20 m,21 m,25 m,30 m,35 m,and 40 m.For the 16 radii,each radius was arranged with 4 measuring points for a total of 64 measuring points.The test TNT equivalent was 90 kg at an altitude of 1500 m,and the measuring point layout radii were 4 m,6.05 m,8 m,9.69 m,and 12 m.The five measuring points were arranged on each radius for a total of 25 measuring points.The test TNT equivalent at 198 m above sea level was 140 kg and 80 kg, the measuring point layout radii were 4 m, 8 m, and 12 m, and 9 measuring points were arranged on each radius. There were 36 measuring points in total.There were certain differences in layout schemes in different environments, but the overall layout concept was the same. A schematic diagram of the overall layout scheme structure is shown in Fig. 2.

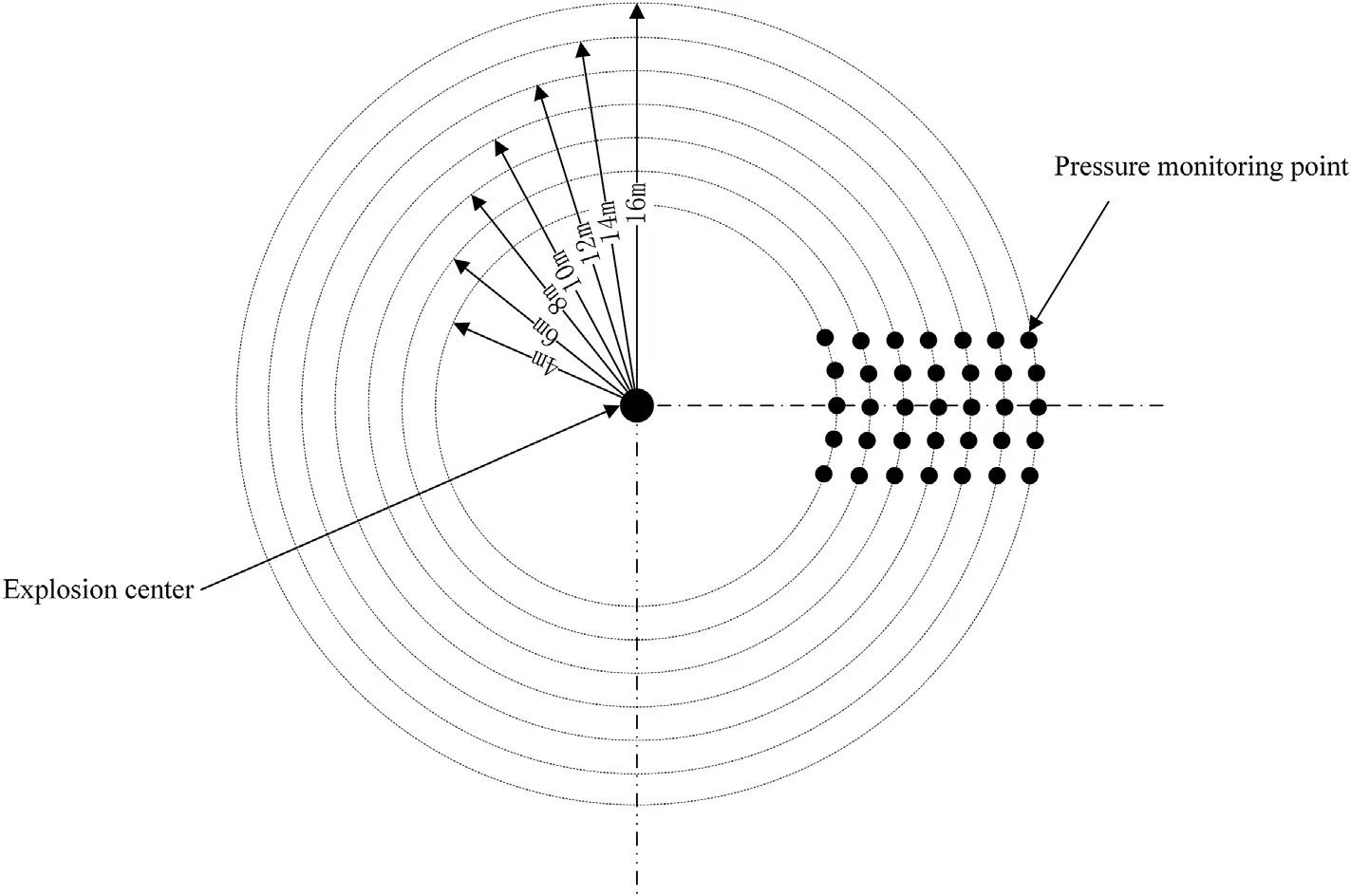
Fig. 2. Overall schematic layout of explosion shock wave measurement points.

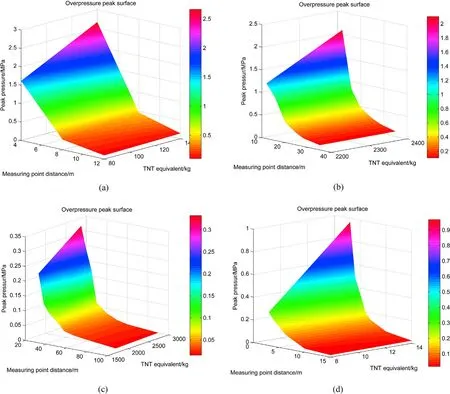
Fig.3. Explosive shock wave toward the overpressure peak surface at different altitudes:(a)Altitude 198 m;(b)Altitude 2000 m(2200—2400);(c)Altitude 2000 m(1700—2750);(d) The altitude is 4650 m.

Fig.4. Explosion shock wave overpressure peak surface:(a)The altitude is 4650 m;(b)The altitude is 2000 m;(c)The altitude is 2000 m;(d)The altitude is 1500 m;(e)The altitude is 198 m.

2.4. Numerical analysis of shock wave

By using the above test plan to test the explosion shock wave under different altitude conditions, as well as processing and analyzing the obtained shock wave data and the shock wave overpressure peak values at different altitudes, different TNT equivalents and different measuring point distances were obtained,as shown in the following Table 1—Table 4.

Table 1Peak value of explosion shock wave overpressure at 4650 m altitude (MPa).

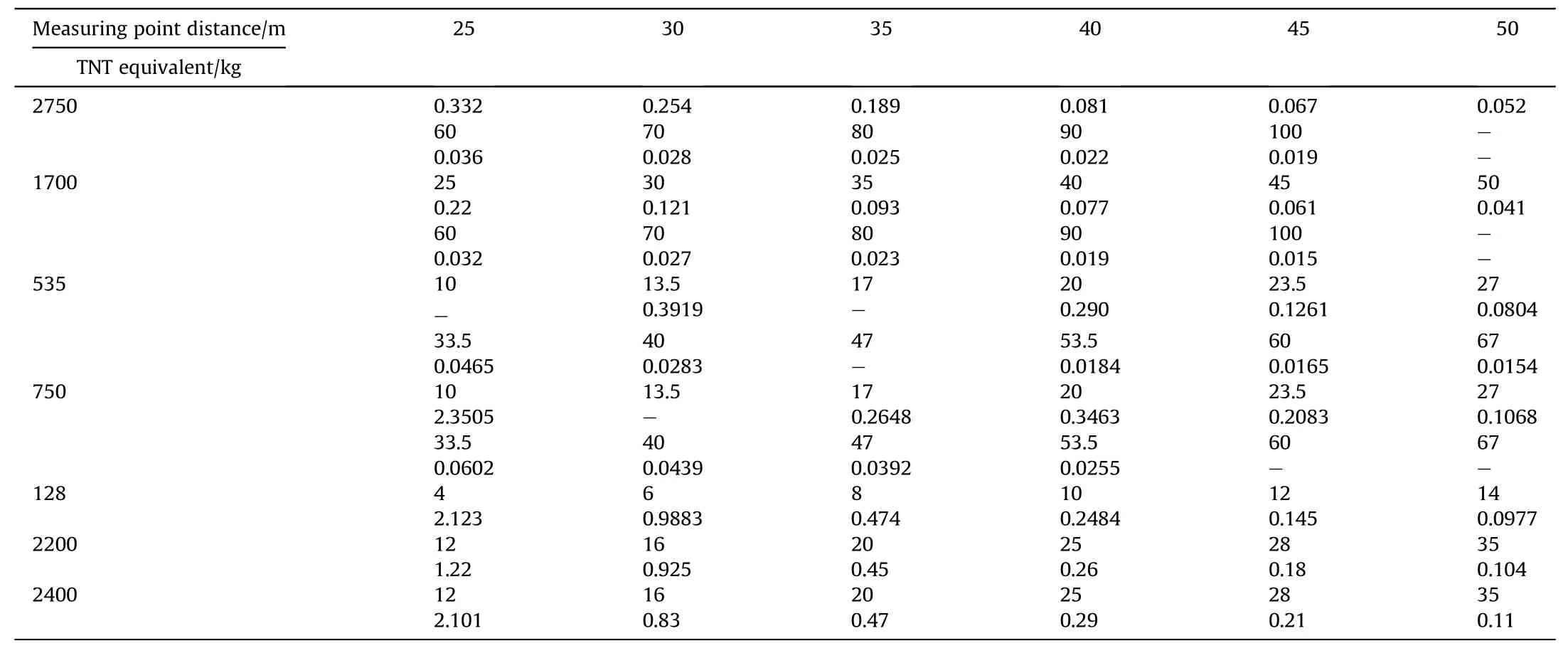
Table 2Peak value of explosion shock wave overpressure at 2000 m altitude (MPa).

Table 3Peak value of explosion shock wave overpressure at 1500 m altitude (MPa).

Table 4Peak value of explosion shock wave overpressure at 198 m altitude (MPa).

The peak data of the explosion shock wave overpressure at four different altitudes, different TNT equivalents and different measuring point distances are shown in the above table. In the above table, the attenuation law of the explosion shock wave pressure with the distance of the measuring point can be seen. To clarify the different altitudes, the attenuation law of shock wave pressure under different TNT equivalents was analyzed. The TNT equivalent was taken as variable X, the distance of the measuring point as variable Y,and the peak overpressure of the shock wave as dependent variable Z.The relationship between the three variables is shown in the figure below.

By analyzing the above shock wave overpressure peak data table and the explosion shock wave attenuation surface, it can be seen that the explosion shock wave overpressure peak gradually attenuates with increasing distance from the measuring point to the explosion center.At different altitudes,the shock wave attenuation rate is different. At an altitude of 4650 m, the shock wave overpressure peak surface in the near field has the largest span;that is,the slope of the curve is the largest, and the overpressure peak attenuation rate is the fastest. With decreasing altitude, the span and slope of the peak overpressure surface decrease, that is, the attenuation rate of the peak overpressure of the shock wave decreases. The peak attenuation rate of shock wave overpressure is positively correlated with the increase in altitude coverage.

The above analysis only analyzes the overpressure peak and altitude from the change trend of the overpressure peak surface.To quantify the above changes in detail, the peak values of explosion shock wave overpressure at four different altitudes were processed to obtain the attenuation rate of shock wave overpressure varying with the distance from the measuring point. The formula for calculating the peak attenuation rate of shock wave overpressure is shown in the following Eq. (3):

wherePnis the shock wave overpressure peak at thenmeasuring point,Pn-1is the shock wave overpressure peak at then-1 measuring point,dnis the distance from thenmeasuring point to the burst center,anddn-1is the distance from then-1 measuring point to the burst center. SincePis pressure, in MPa, anddis distance, inm, the unit of shock wave overpressure peak attenuation rate ξ is (see Fig. 3) MPa／m.

According to the above calculation formula,the attenuation rate of the explosion shock wave overpressure peak value at four different altitudes with distance is shown in Table 5—Table 8. The data in the tables are graphed and analyzed, and the attenuation rate curve is shown in Fig. 4.

Table 5Explosion shock wave overpressure peak attenuation rate table at 4650 m altitude (MPa/m).

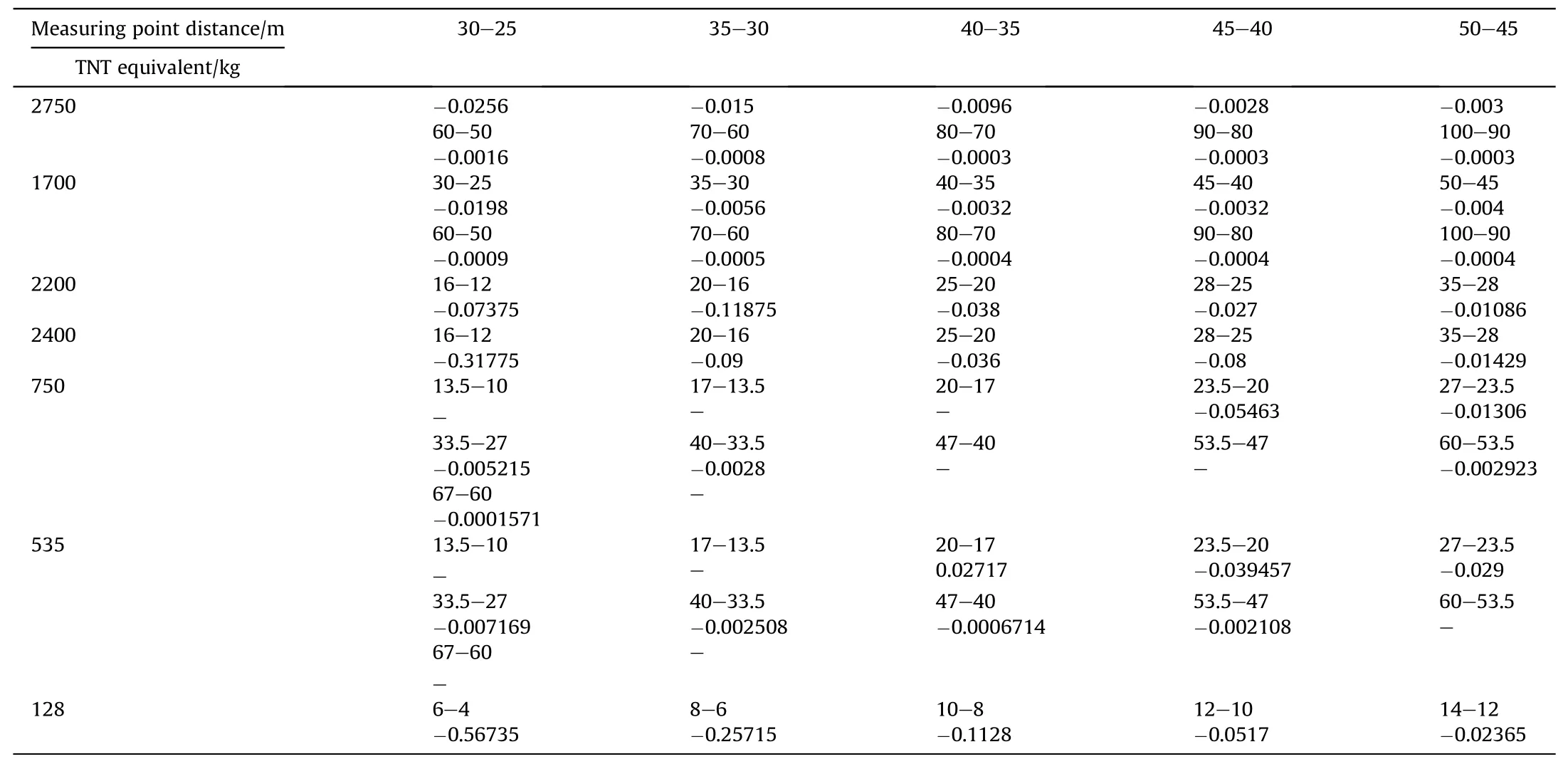
Table 6Explosion shock wave overpressure peak attenuation rate table at 2000 m altitude (MPa/m).

Table 7Explosion shock wave overpressure peak attenuation rate table at 1500 m altitude (MPa/m).

Table 8Peak shock wave overpressure peak attenuation rate table at 198 m altitude (MPa/m).

By analyzing the abovementioned explosion shock wave overpressure peak value and overpressure decay rate curve, it is concluded that (1) the explosion shock wave overpressure peak value gradually attenuates as the distance between the measuring point and the burst center increases,but the attenuation process is not equal,and the main manifestation is the distance from the burst center. The decay rate of overpressure is fast near the center, and the decay rate of overpressure is slow far away from the explosion center; that is, the overpressure decay rate of the explosion shock wave is negatively correlated with the proportional distance. (2)Under the same test environment and different TNT equivalents,the peak overpressure of the blast wave increases with increasing TNT equivalent. In the area close to the explosion center, the explosive shock wave overpressure is significantly affected by the quality of the charge.In the area far away from the explosion center,the overpressure of the blast wave is less affected by the charge mass. However, overall, the overpressure of the explosive shock wave is positively correlated with the charge quality.(3)As the TNT equivalent increases, the peak attenuation rate of the explosive shock wave overpressure at the same measuring point distance isnegatively correlated with the TNT equivalent. The larger the TNT equivalent is, the smaller the peak attenuation rate of the shock wave overpressure within the same measuring point radius. The main reason is that the three-wave point height of the shock wave is negatively correlated with the charge quality.The larger the TNT charge quality is,the lower the three-wave point track height,and the weaker the Mach reflection disturbs the shock wave pressure,which makes the shock wave pressure attenuation rate smaller.Under the same TNT equivalent,the shock wave attenuation rate in the near-field area is greater than that in the far-field area.The main reason is that fragments and flying rocks produced by the near-field explosion will attenuate the shock wave pressure to a certain extent.The surface propagation medium is within the range of the explosion center.As shock waves and fragments lift up the soil,thenegatively related to the charge quality.For example,at an altitude of 4650 m,for a TNT equivalent of 8 kg,the explosion for a 3—15 m peakattenuationrateofshockwaveoverpressure is-0.00668 MPa/m/kg;when the TNT equivalent is 14 kg,the peak attenuation rate of explosion shock wave overpressure from 3 to 15 m is-0.0179675 MPa/m/kg;at an altitude of 2000 m,for a TNT equivalent at 1700 kg,the peak attenuation rate of explosive shock wave overpressure from 25 to 100 m is-2.558 2 MPa/m/kg;when the TNT equivalent is 2200 kg, the peak attenuation rate of explosive shock wave overpressure from 12 to 35 m is-2.43964 MPa/m/kg; when the TNT equivalent is 2750 kg,the peak attenuation rate of the explosion shock wave overpressure from 25 to 100 m is -2.15636 MPa/m/kg.

It can be seen from the above analysis at the same altitude that the peak attenuation rate of the blast shock wave overpressure is ground becomes softer.During the propagation of the shock wave,the energy absorption is larger, resulting in weaker reflection,which makes the shock wave attenuation rate in the near field larger than that in the far field.

3. Establishment of the engineering numerical model

Based on the above analysis, it can be seen that with different geographical locations and altitudes, the peak overpressure of the explosion shock wave at the same proportional distance will change with changes in altitude. The current functional relationship used to calculate the peak overpressure of the explosion shock wave cannot meet the requirements.The peak value of shock wave overpressure is calculated at different altitudes. Therefore, this paper analyzes the abovementioned shock wave overpressure peakdata at different altitudes. Adding the correction effect of atmospheric pressure on the shock wave pressure to the original formula for calculating the peak overpressure of the explosion shock wave,the formula for calculating the peak value of the explosion shock wave with the correction coefficient of the atmospheric pressure is obtained.

The theoretical analysis of the impact of different altitudes on the shock wave pressure distribution is mainly reflected in the large differences in atmospheric pressure at different altitudes. Atmospheric pressure directly affects the air density in the test environment. According to existing research data, the air density directly affects the shock wave pressure and the propagation speed of the wave front, which is specifically expressed as the lower air density (the higher the altitude). At the same measuring point of the same TNT equivalent, the peak value of shock wave overpressure decreases,while the propagation speed of the shock wave front increases. In a vacuum environment, the shock wave explosion product is the medium propagation, and the propagation distance of the explosion product has a linear relationship with time. The calculation function relationship between altitude and atmospheric pressure is as follows.

According to the spherical shock wave pressure generated by the explosion of a TNT concentrated charge in a semi-infinite space,there is a positive correlation withPH／P0, wherePHis the atmospheric pressure at altitudeHandP0is the standard atmospheric pressure.Therefore,the higher the altitude is,the smaller the shock wave pressure at the same measuring point, and the atmospheric pressure is negatively correlated with the shock wave pressure.

Based on the above analysis,the thesis is based on the Sadowski formula.On the basis of the formula,the corresponding air pressure correction factor is added to obtain the calculation formula of the explosion shock wave overpressure under the influence of atmospheric pressure. Assuming that the peak overpressure of the explosion shock wave calculated by the Sadowski formula isPnormal,the influence factor of the atmospheric pressure on the peak overpressure of the explosion shock wave is φ, and the peak overpressure of the explosion shock wave under the influence of different atmospheric pressures is expressed asPfix, then the atmospheric pressure is introduced.The calculation function relation of the influence factor of the explosion shock wave peak overpressure can be expressed as

In the above expression,Pnormalselects the most commonly used Sadowski formula to calculate the peak overpressure of the shock wave at different measuring point distances.The Sadowski formula is shown in the following equation:

In the abovementioned Sadowski formula,Pis the peak overpressure of the explosion shock wave, in MPa, anda1,a2,a3is the coefficient related to the explosion environment. When selecting the value, an appropriate value can be selected according to the actual explosion environment. Substituting into the abovementioned functional relationship, in this article, according to the actual test environment, we choosea1= 0˙102,a2= 0˙399, anda3= 1˙26.ris the distance between the measuring point and the center of the explosion,in,andwis the explosive TNT equivalent,in kg. Generally,is taken as a whole and expressed byR.Ris called the proportional distance,and the unit is m／kg1／3.Therefore,the above Eq. (5) can be expressed as

Using the functional relationship established by Eq. (7) to analyze and fit the peak overpressure data of the explosive shock wave under different atmospheric pressures,the expression of the peak overpressure correction factor φ of the explosive shock wave under the influence of atmospheric pressure is obtained as Eq.(8),whereP1is the corresponding atmospheric pressure at different altitudes.

By combining the atmospheric pressure correction factor of the above Eq. (8) with the Sadowski formula, the calculation function relation formula for the peak overpressure of the explosion shock wave containing the atmospheric pressure correction factor is

By substituting the abovementioned measured data into the functional relationship to calculate the peak overpressure of the explosion shock wave at different atmospheric pressures, one can calculate the relative error rate between the measured data and calculated data of the functional relationship according to Eq.(10).The calculation results are shown in Table 9.

Table 9Comparison and analysis table of measured results and calculated results.

In comparing and analyzing the above measured results and calculated results,it can be seen that maximum error between the measured value and the calculated value occurs when the altitude is 2000 m,the distance between the measuring points is 35 m,and the peak value of the measured shock wave overpressure is 0.189 MPa. The shock wave calculated by the formula peak overpressure is 0.22678 MPa, and the error rate between the two is 19.98942%. The minimum error between the measured value and the calculated value occurs at an altitude of 4650 m,the measuring point distance is 3 m,the measured shock wave overpressure peak is 0.2925 MPa, and the calculated formula shock wave stamping peak value is 0.285806 MPa,with an error rate between the two of 2.28855%. The error rate between the measured and predicted values of the explosion shock wave at other altitudes lies between the two. To calculate the functional relationship prediction accuracy of the explosion shock wave peak overpressure at different altitudes, the average value between the two is taken as the calculation accuracy of the functional relationship. The calculation relationship is as follows:

According to Eq. (11), the prediction accuracy of the functional relationship is 11.1389%, so the functional relationship has high accuracy in predicting the peak overpressure of explosive shock waves at different altitudes and can respond well to explosions.There is a relationship between the peak value of shock wave overpressure and altitude, so this functional relationship can be applied to actual engineering tests.

4. Conclusions

Through an analysis of the abovementioned explosion shock wave overpressure peak data at different altitudes and different proportional distances, the basic propagation law of the explosion shock wave at different altitudes is obtained, and the abovementioned explosion shock wave overpressure peak value is fitted with a functional relationship. The formula for calculating the explosion shock wave peak overpressure with the correction factor of atmospheric pressure is obtained.

(1) The general distribution and attenuation of the explosion shock wave at different altitudes are basically the same.The peak of the explosion shock wave overpressure near the explosion center is larger, and the peak of the explosion shock wave overpressure far away from the explosion center is smaller. As the distance from the measuring point to the explosion center increases, the peak of the shock wave overpressure gradually attenuates.

(2) With the difference in altitude, there are differences in the peak overpressure of the explosive shock wave at the measuring point under the same proportional distance, and there is a negative correlation with the altitude. Under the same proportional distance, the peak value of the explosive shock wave overpressure gradually decreases with increasing altitude.

(3) In this paper,based on the Sadowski formula,by considering the influence of atmospheric pressure on the peak ofexplosive shock wave overpressure,a formula for calculating the peak value of explosive shock wave overpressure at different altitudes with an atmospheric pressure correction factor is established, and the measured data verify the accuracy of the functional relationship.The verification results show that the maximum relative error rate of prediction is less than 20%,and the average relative error rate is less than 11.1389%.Therefore,this function has a high performance in predicting the peak overpressure of explosion shock waves at different altitudes. This accuracy can be used in actual projects to provide an effective method for the calculation and analysis of the peak overpressure of explosive shock waves at different altitudes.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.