Study on the prediction and inverse prediction of detonation properties based on deep learning

Zi-hang Yang, Ji-li Rong, Zi-tong Zhao

Department of Mechanics, School of Aerospace Engineering, Beijing Institute of Technology, Beijing,100081, China

Keywords:Deep learning Detonation properties KHT thermochemical Code JWL equation of states Artificial neural network One-dimensional convolutional neural network

ABSTRACT

1. Introduction

Energetic materials include propellants, explosives, and pyrotechnics, covering fields ranging from military weapons to the aerospace industry.Energetic materials have played a pivotal role in human history.In the field of military weapons,since World War II,weapon designers have been devoted to finding new energetic materials with excellent detonation performance, stable thermodynamic properties, and safety. This requires the prediction of the explosive properties of new molecules or new formulations. The detonation properties of an explosive determine the extent of damage by the explosive to the target.The detonation properties of explosives mainly include the properties of the detonation wave(detonation parameters) and the subsequent expansion of detonation products. The determination of detonation properties is a prerequisite for weapon design; therefore, the weapon's warhead can be designed only after the detonation properties of the explosive are determined. Because of the danger and high cost of explosion experiments, most studies on the damage ability of weapons are conducted through numerical simulation methods.Numerical simulations include shock wave and bubble pulsation simulation of underwater explosions [1], armor-piercing damage simulation of weapon warheads[2],and explosive-driven cylinder working simulations [3]. The detonation parameters and working capacity of explosives are indispensable parameters in numerical simulations,and the determination of the detonation properties of explosives is an indispensable link in weapon design research,which is of great engineering significance.

Presently, the main methods for determining the detonation parameters of explosives without experiments include the empirical formula, thermochemical calculation method, and quantum chemical calculation methods.The empirical formula method only requires the molecular composition of explosives as an input, and various parameters of explosives can be obtained through a simple operation.The most classical empirical formula is the Kamlet Jacobs formula [4]. Another commonly used prediction method is the thermochemical calculation method.The thermochemical program is compiled based on the free energy minimization and Chapman-Jouguet (CJ) theory. The determination of concentration of detonation products is based on free energy minimization and the detonation properties are calculated based on CJ condition. Researchers have developed thermochemical programs based on various equations of state (EOS) to predict the detonation parameters of explosives, such as the EXP-6 [5], BKW [6], VLW [7], and KHT equations of state [8]. Since the 20th century, the quantum chemical method [9] has been applied in energetic-material calculations and screening [10], and it can calculate the theoretical detonation parameters of molecules [11]. These three calculation methods have advantages and disadvantages. The empirical formula method is fast and simple;however,its scope of application is limited. Furthermore, ensuring its effectiveness for new explosive formulations or molecules is difficult. The thermochemical calculation method can be applied to new molecules or composite explosives with diverse components; however, it has complex programming and is difficult to apply [12]. Quantum chemical methods such as density functional theory have a wide range of application,but the calculation time is long and requires significant computing resources [13]. Therefore, it is important for weapon designers to develop a simple, fast, and universal new method to predict the detonation properties of explosives.

In recent years, with the continuous improvement of machine learning methods and computer performance, researchers have introduced machine learning methods in the fields of chemistry and materials[14],which can be used to predict the performance of materials. The deep learning method [15] is a type of machine learning method and is based on the artificial neural network(ANN). It requires original data, including the input and output of the problem to be studied to train a deep learning model. This model can then be used to predict the output results of the original problem or for identification and classification. After training, the deep learning model can realize the rapid prediction of results and solve some inverse predictions. In recent years, researchers have gradually applied machine learning and deep learning methods to predict detonation parameters [15—20]. First, information on the detonation parameters or crystal density of various molecules is obtained from the database, and certain molecular descriptors(such as the Coulomb matrix [16], simplified molecular input line entry system (SMILE) descriptor [17], molecular fingerprint [18],oxygen balance, or directly using the atomic composition of molecules [12]) are used to describe the molecules as the input of the training set. Detonation parameters are taken as the output, and various machine learning algorithms such as kernel ridge regression [16],support vector machine method[19],and random forest algorithm [20] or deep learning algorithms such as graph neural networks [19] and convolution neural networks [21] can be used.After training with the data from the database, the model can predict the detonation parameters of the explosive molecules.

Contrast to the quantum chemistry method or the thermochemical calculation method, the detonation parameters calculation model based on deep learning can avoid long calculation times.It can predict the detonation parameters of explosives in a short time after training. Furthermore, it has the advantages of simple use and rapid prediction. The prediction results can meet the engineering requirements through reasonable model parameter settings.Weapon designers who are unfamiliar with quantum chemical calculations can also simply and quickly predict the detonation properties of explosives through this method.However,some problems persist in the prediction model of explosive detonation parameters based on deep learning established by researchers. First, the scope of its application is limited. Presently,most explosive detonation parameters prediction models based on deep learning focus on explosives consisting of single molecules,while actual weapon warhead explosives are mostly mixed explosives.Mixed explosives can complement the advantages of various other explosives. To guide actual weapon warhead design, a deep learning model that can simply and quickly predict the detonation properties of mixed explosives is required. Second, most current detonation property prediction models based on deep learning can effectively predict the detonation parameters. However, for engineering design,to simulate the damage performance of explosives,the equation of state parameters of explosives (such as JWL EOS)are used in addition to detonation parameters.The equation of state is generally determined using cylinder experiments [22]. Furthermore, the parameters of the equation of state of explosives with different charge densities are also different. Although the deep learning method is suitable for solving the problem of parameter dependence in experiments, there are almost no deep learning models that directly predict the parameters of the equation of state of explosives after detonation in literatures. Finally, inverse prediction was seldom considered in literatures. For engineering design, the inverse prediction of explosive detonation has more engineering significance,that is,it is significant for the prediction of the composition of explosives according to their properties. Chandrasekaran et al.[12]conducted a simple inverse prediction study.First, a direct prediction model was established to predict the detonation velocity of explosives by taking the CHNO atomic component, heat of formation, and charge density as inputs, and good prediction results were obtained. Subsequently, inverse prediction was studied.The N and O atomic components of explosives was predicted by the detonation velocity, C and H atomic components, and charge density. The results were tested, and the prediction was accurate for most of the explosives in the validation set.Therefore, it is reasonable to apply a deep learning method to the inverse prediction of explosive detonation.

Aiming at solving the problems existing in the current explosive detonation parameters prediction model based on deep learning,this study established three improved models based on an ANN method and a one-dimensional convolutional neural network(CNN1D). These are a detonation parameters prediction model based on an ANN,a JWL EOS parameters prediction model based on an ANN, and an inverse prediction model. The training and validation data of all three models were obtained from the KHT code.

The detonation parameters prediction model can predict the detonation parameters of explosives according to the mass fraction of the input explosives and the charge density, the JWL EOS parameters prediction model can predict the JWL equation of state parameters of explosives according to the mass fraction and charge density of the input explosives, and the inverse prediction model can predict the mass fraction of explosive components and the charge density according to the detonation parameters of the input explosive and the isentropic expansion curve of the explosive.

This paper is organized as follows. In the next section, some models and methods applied in this study are introduced,including the method of using the KHT thermochemical code to predict the detonation parameters and the JWL EOS parameters to obtain the original data. A deep learning model, which is the core method of this study,is introduced in this section.In Section 3,to achieve the prediction and inverse prediction of explosive properties, three models are established using the model in Section 2.These are the detonation parameters prediction model, the JWL EOS parameters prediction model,and the inverse-problem model.The structure of the three models and how to establish and examine them are introduced in detail in Section 3. In Section 4, the results after model training are discussed, and a short summary is provided in Section 5.

2. Model and method

This study is expected to establish a model for predicting the properties of explosives with explosive formulations as the input or to predict explosive formulations with properties of explosives as the input. The algorithms or models that must be applied in this process are as follows. First, the KHT thermochemical code is applied to solve the explosive detonation parameters and isentropic expansion curves.Second,two types of deep learning models were applied: an ANN model and a CNN1D model. The relationships between these models are shown in Fig.1.

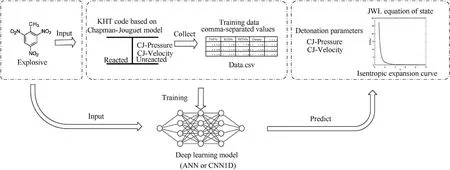
Fig.1. Schematic of the relationship between the deep learning model and KHT code.

First, we input the explosive formulations into the KHT thermochemical code to calculate the detonation parameters and the isentropic expansion curve of the JWL state equation. Second, a large amount of calculated data is input into the deep learning model(ANN and CNN1D model)for training.The trained model can directly predict explosive detonation parameters, JWL state equation parameters, or explosive formulations according to the explosive performance. The ANN and CNN1D models are mainly used to describe the relationship between explosive formulations and explosive properties. These were the core models used in this study. The KHT thermochemical code was mainly used to provide the original data for model training.These models are described in detail below.

2.1. Prediction of detonation parameters using KHT code

To establish the relationship between the explosive formulations and detonation parameters, the original data must first be obtained. The training data of the neural network model in this study were obtained using the KHT thermochemical code [23].

The KHT thermochemical code was programmed based on the KHT equation of state[24]and CJ theory.The KHT equation of state is given by Eq. (1)

where,a,b,c,d,e,n,λi,α are constant parameters.Xiis the molar fraction of each detonation product,Xis an intermediate variable,andp,v,Tare the thermodynamic quantities.

First, the components of the detonation products are solved iteratively using a computer,and then the basic equations of the CJ theory are solved using the thermodynamic quantities of the KHT equation of state. Using the properties of the CJ condition as the convergence conditions, the detonation pressure, detonation velocity, and other parameters of the explosives can be solved. According to the atomic composition, mass fraction, heat of formation, and charge density of the explosives, the KHT thermochemical code can be used to calculate the detonation parameters.A large amount of training data can be obtained by generating various explosive formulations. The detonation parameters and isentropic expansion curve calculated using the KHT thermochemical code were verified to meet engineering accuracy requirements [23]. Through the KHT thermochemical code, training data for the neural network model can be obtained.

2.2. Prediction of JWL EOS parameters using KHT code

The JWL equation of state is the equation that measures the work ability of explosives[25],the isentropic equation of JWL EOS is shown in Eq. (2).wherePsis the isentropic pressure.Vis the specific volume,andA,B,R1,R2,C,ω are the unknown parameters.

The JWL equation of state parameters is generally determined using a standard cylinder experiment [22]. However, cylinder experiments are complex and expensive. The JWL EOS parameters of explosives with different charge densities are also different,and they must be determined independently by cylinder experiments.Therefore,a method that does not utilize an experiment is required to obtain the parameters of the JWL equation of state of explosives with different mass fractions.

The KHT thermochemical code can be used to calculate the isentropic expansion data after an explosion. The isentropic equation of the JWL equation of state must pass through the isentropic expansion point calculated by the KHT thermochemical code, and the starting point of this process is the CJ detonation point.Therefore, the JWL EOS should satisfy the following equations shown in Eq. (3)

These equations are often used to be the constraint of JWL EOS.For example, LLNL [26] use this simultaneous equation as the constraint to fit their JWL EOS parameters from cylinder test.

2.3. Deep learning method

The deep learning method [15] is a machine-learning method developed based on the ANN method.In this study,an ANN model[27] and a CNN1D model [28] were used to establish the relationship between explosive formulations and explosive properties.These methods are subsequently discussed in detail:

The ANN model method is a multi-objective optimization algorithm that is widely used in fitting data without equations and exploring the correlation contained in data.This method is suitable for the prediction problem. The ANN model was composed of a multilayer neuron structure. Neurons are the core of ANN models.The function of each neuron is to connect the upper and lower neurons through an activation function and finally generate a complex neural network.The mathematical description of a single neuron is as follows:

wherewiis the weight,xiis the input from the upper layer,bis the bias, andfis the activation function, which is typically a Sigmoid function or rectified linear units (ReLU). The calculatedyis the output for this layer and the input for the next layer.In this manner,the neurons of all layers can be connected to an entire neuron network.

The process of establishing and solving an ANN model involves determining the weights and biases of the neurons.In this process,an index is required to evaluate the model.This evaluation index is known as the loss function.There are many types of loss functions,such as mean square error(MSE)or cross entropy.The MSE is often used as a loss function in regression problems. The MSE is defined as:

The MSE represents the mean square error between the calculated and actual values of the neural network.The purpose of determining the best neuron weight in the neural network is to reduce the loss function value as much as possible. The process of determining the neuron parameters of the network is known as training. The training model often requires a large amount of data to ensure the effectiveness of the training. The training model is generally realized using the stochastic gradient descent(SGD) and back propagation (BP) methods. The mathematical description of the SGD is as follows:

wherepis a vector consisting of weights and bias.η is the step size,which is usually called the learning rate, andNis the number of training samples. By iterating the SGD, the loss function can be optimized as much as possible. In this process, the gradient of the loss function to the weights must be solved. In this process, back propagation can solve the gradient through the chain rule.

By combining the above neural network structure with the solution method, the neural network can be trained using a large amount of data. The trained model can establish the relationship between input and output in the provided data and can predict the output results according to the input, which is similar to human“learning” behavior.

The CNN1D model is a neural network method that adds feature extraction layers,such as convolution and pooling layers,based on an ANN model.For this study,it was necessary to establish a neural network model for the isentropic expansion curve (sequence) of explosives. If all curve points are input into the ANN network for operation, the operation will be slow, and it will be difficult to analyze the characteristics.Therefore,a CNN1D model was adopted.

The convolution layer was used to extract image or sequence features. Longer sequence information was extracted into shorter feature information through a convolution operation. Convolution layer is the process of using convolution to check the original sequence for convolution. For one-dimensional convolution, the processing process of the convolution layer is as follows:wheresis the new sequence after convolution,fandgare the original sequence and convolution kernel, respectively.Nmeans the different position in the sequence.

The convolution layer can extract the image features. The pooling layer generally divides the sequence into several parts and uses the average or maximum value to represent each part in order to achieve dimension reduction. The pooling layer alleviates the excessive sensitivity of the convolution layer to the position, improves the computing speed, and increases robustness. After the features are extracted from the convolution and pooling layers,the input information passes through a flattened layer to compress all the parameters into a vector. At this time, the features of the sequence are abstracted into this vector, which is then input into the full connection layer for training.A complete one-dimensional convolution neural network model was established. The structure of the fully connected layer was similar to that of the ANN model.

The platform for establishing the deep learning model in this study is Tensorflow[29],which is based on the Python language.It is an integrated deep learning research framework, and it is convenient for users to establish layer structures and tests. The corresponding Python programs are compiled to build the model structure and input data to train and test the model.

2.4. Brief summary

In this section,some basic models that are necessary to establish the prediction and inverse prediction model of explosive detonation performance are introduced, including the KHT thermochemical code used to collect the original data and the deep learning models (ANN and CNN1D models) used to establish explosive composition and explosive performance. First, the training data are through the KHT thermochemical code. Subsequently,the parameters of the neurons in the deep learning model can be determined through the training solution, so that the function of directly predicting the performance of explosives or the formula of explosives can be realized through the model. The specific process of model establishment,training,and examination is described in detail in the next section.

3. New models of detonation properties

Based on the model introduced in Section 2,three models were established using the deep learning method in this section. These are the detonation parameters prediction model, the JWL EOS parameters prediction model, and the inverse prediction model for predicting the explosive formulations according to the isentropic expansion curve of the explosive and the detonation parameters.The three models are progressive,from simple to complex,and the goal is to predict the detonation parameters and JWL EOS parameters of the mixed explosives using the established model and to predict the composition of the explosives according to their detonation properties. The structure of this section is illustrated in Fig. 2.

The model was divided into three stages: data collection,training,and validation. In the data collection stage,explosive formulations (including mass fraction and charge density) were generated. The detonation parameters, JWL EOS parameters, and isentropic expansion curve were calculated using the KHT thermochemical code. After data collection, the data were applied to the ANN and CNN1D models for training.After model training,the model was validated. The validation process was divided into validation-set model test and validation of the model accuracy. In the validation of validation-set model test, the training effect was tested,and it was judged whether the model was over-fitting using the data not utilized in the training. In the model accuracy validation, it was verified whether the engineering accuracy was met using the reference data of explosives given in the LLNL explosives manual and other literatures [30—33]. The model establishment process is described in detail below.

3.1. Detonation parameters prediction model based on ANN

3.1.1. Data collection

Before establishing the model, the molecular descriptor of the problem and the explosive formulations should be defined. For weapon warheads, the basic explosive types are TNT, RDX, and HMX. Although a variety of new energetic materials have been selected in existing research [34], it is still some time before they can be used in warheads. Therefore,the mixed explosives of these three explosives were selected as the research object in this study,and the variables were the mass fraction of the three explosives and the charge density. In the deep learning model established by Chandrasekaran et al.[12],the CHNO,heat of formation,and charge density were used as model inputs. In their model, because the CHNO values or proportions of different mixed explosives may be the same, the heat of formation was added to distinguish these explosives. However, this problem does not occur in the model in this study because the components of fixed types of condensed explosives(TNT,RDX,and HMX)are used.The heat of formation has been included in the explosive category, so the heat of formation term is not required. Training data were generated using the KHT thermochemical code.The input of the data are the mass fractions of TNT,RDX,and HMX,as well as the charge density.The outputs of the data are the detonation pressure and detonation velocity. In total,10,000 groups of data were generated as the original model data. The original data were divided into a training set and a validation set using the ratio of 7:3, and the validation set was not utilized in the training.

Because of the different dimensions, ranges, and orders of magnitude of the mass fraction, charge density, detonation pressure,and detonation velocity of explosives,to avoid the problem of uneven weight distribution or slow convergence in the deep learning program, the data utilized in the training and validation were normalized by Z-score normalization, that is

wherex* is the training data after normalization,Xis the original training data,μ is the mean value of the training data,and σ is the standard deviation of the training data.

Z-score normalization can make the data dimensionless and only considers the degree to which the output deviates from the average in the training,accelerates the convergence,and simplifies the model.

3.1.2. Model establishment

The Python program was compiled based on the TensorFlow framework and a GPU was used for calculation.Because the model requires multiple inputs and outputs, the Keras functional model was used to establish it. The established deep learning network model is illustrated in Fig. 3.

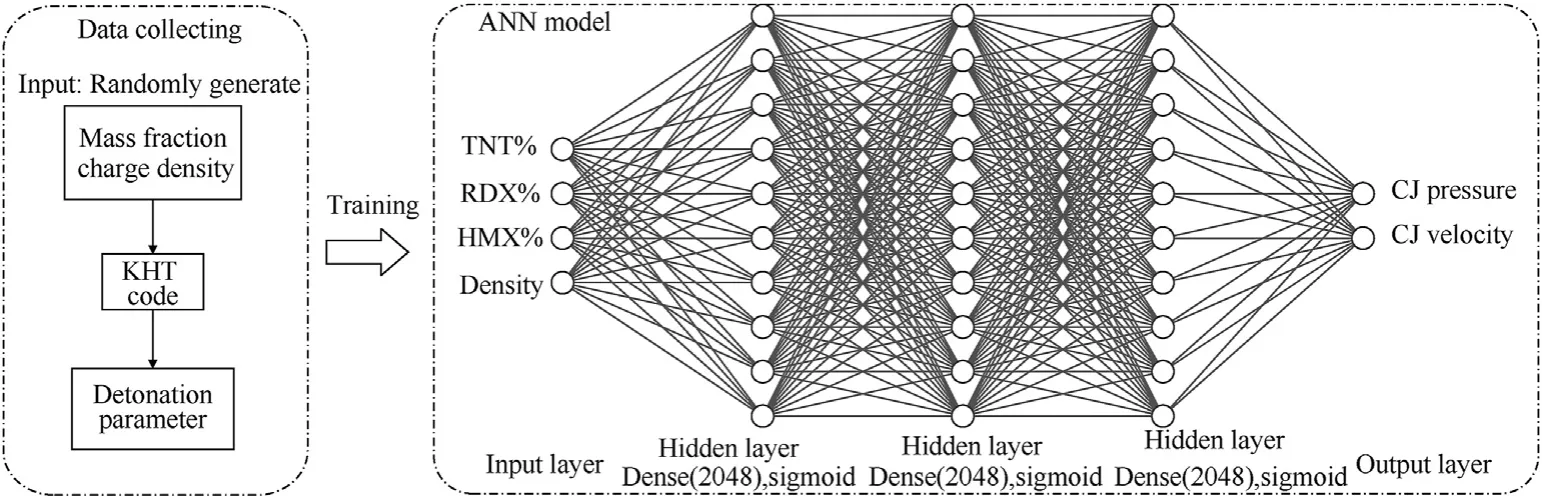
Fig. 3. Schematic of the structure of the detonation parameters prediction model.

The model consisted of an input layer, three hidden layers, and an output layer. The input layer included the mass fraction and charge density of explosives.Each hidden layer consisted of a fully connected dense layer with 2048 nodes, a dropout layer, and a batch normalization layer, which was used to prevent overfitting and improve the learning effect.The sigmoid function was adopted as the activation function, and the output layer consisted of the detonation pressure and velocity.The mean square error(MSE)was used for the loss function of this model, and the training epochs were 1000.

3.1.3. Model validation

After model training, the original data not utilized in the training were used as the validation set to test the training results of the deep learning model. The explosive formulations in the validation set were input into the deep learning model to predict detonation parameters. Subsequently, a predicted detonation parameter value was obtained, which was compared with the detonation parameters corresponding to the formulations in the validation set (reference values). The fitting effect between the predicted and reference values is characterized by the correlation coefficient (R-square),which is defined as

wheremis the total number of predicted points,yiis the reference value,is the predicted value,andis the average of the reference values.

The fitting error is characterized by the root mean square error(RMSE), which is defined as

The closer theR-square value is to 1,the better the fitting effect;the closer the RMSE is to 0,the smaller the fitting error.These two indicators can be used to evaluate the fitting effect of the model and the occurrence of overfitting. For a deep learning model, if the trained model relies too heavily on its training set and has a poor effect on the validation set, this phenomenon is called overfitting.TheR-squared value and RMSE of the prediction result of the validation set can be used to determine whether the model is overfitted.When theR-squared value of the prediction result of the validation set is very small or the RMSE is very large, it is an indication that the model is overfitted and cannot accurately predict the data outside the training set.On the contrary,anR-square close to 1 and a small RMSE indicates that the model avoids the problem of over-fitting, and the trained model is more generalized. The trained model can show the real input-output relationship of the data rather than “memorizing” the data in the training set.

The model was applied to explosives with real formulations to test its accuracy, the detonation parameters were predicted, and their values were compared with the reference values in the LLNL explosives handbook and other Refs. [30—33]. The accuracy of the model was evaluated directly using the error between the predicted and reference values.The validation set test can only test the model.The essence of checking whether the model is over-fitted is to determine whether the neuron weights and bias in the model are correct. The accuracy test can determine whether the neuron parameters trained by the model can reach the engineering accuracy for the prediction of real explosive properties.

3.2. JWL EOS parameters prediction model based on ANN

The JWL EOS is an important equation for measuring the working capacity of explosives. In this study, the relationship between the explosive formulations and parameters of the JWL EOS was established using an ANN model. The parameters of the JWL EOS can be predicted by the model based on the explosive formulation.The establishment process of the model was similar to that of the detonation parameters prediction model, which also included data collection, model establishment, and model validation.

3.2.1. Data collection

Similar to the detonation parameters prediction model based on the ANN, the original data were calculated using the KHT thermochemical code, the mass fraction and charge density of explosives were used as inputs,and the parameters of the JWL EOS were used as outputs. Ten thousand groups of training data were obtained, which were divided into training and validation sets at a ratio of 7:3.

3.2.2. Model establishment

The Keras functional model under the TensorFlow framework was also used to establish the deep learning model.The structure of the model is illustrated in Fig. 4.

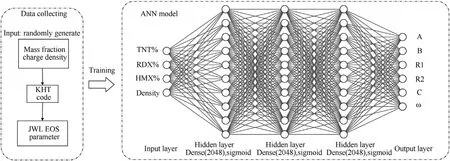
Fig. 4. Schematic of the structure of the JWL EOS parameters prediction model.

The structure for is similar to the detonation parameters prediction model. The output layer is different, which contains the parameters of JWL EOS.

3.2.3. Model validation

Similar to the detonation parameters prediction model,the JWL EOS prediction model requires two tests:a validation set test and a model accuracy test. The validation set test was used to compare the JWL EOS parameters of the predicted values of the model with the JWL EOS parameters of the reference values from the validation set.

For the accuracy test of the model, the formulations of real explosives were input into the trained model to predict the JWL state equation parameters. Subsequently, the values predicted by the model were compared with the reference values in the literatures to verify their accuracy.

3.3. Inverse prediction model based on CNN1D

In this study, the inverse prediction model for explosive prediction is established using the deep learning method; that is, a model is established,for which the formulation of explosives can be predicted by inputting detonation parameters and JWL EOS parameters. The inverse prediction model for explosives has engineering significance.

3.3.1. Data collection

In the process of modeling inverse prediction, the problem of the JWL EOS should be solved first.The parameters used in the JWL EOS parameters prediction model were fitted using the KHT thermochemical code. Although they have very high fitting accuracy, they may not be the global optimal solution. The isentropic expansion curves corresponding to different JWL EOS parameters may be the same; however, the isentropic expansion curve (pressure vs.specific volume)corresponding to the formulation is fixed.This means that, for an explosive formulation, there may be many different sets of EOS parameters that meet the engineering requirements, which will not cause issues in the forward problem.However,in inverse prediction,because the input and output are to be exchanged,the parameters of the JWL EOS are used as the input,while the explosive formulations are used as the output, which results in multiple solutions or difficulty in convergence.Therefore,the fitted parameters of the JWL EOS cannot be used, and the JWL isentropic expansion curve should be used directly as the input.The isentropic expansion curve is one-to-one, corresponding to the explosive formulation, so the problems above will be avoided. In the data generation process of the inverse prediction model,explosive formulations with random mass fractions and charge densities are generated first. The detonation parameters and the JWL isentropic expansion curve (sequence) were calculated using the KHT thermochemical code, and the two were reversed when forming the training and validation sets.The input of the model is a combination of detonation parameters and the JWL isentropic expansion curve, and the output is the corresponding explosive formulations.The ratio of the training set to the validation set was 7:3.

3.3.2. Model establishment

Using the isentropic expansion curve as an input implies that the number of input items may be very large, up to thousands of input items, which makes it difficult to carry out deep learning training. Therefore, for the isentropic expansion curve, the onedimensional convolution neural network method was used to extract the features and simplify the problem.The established deep learning model is shown in Fig. 5.

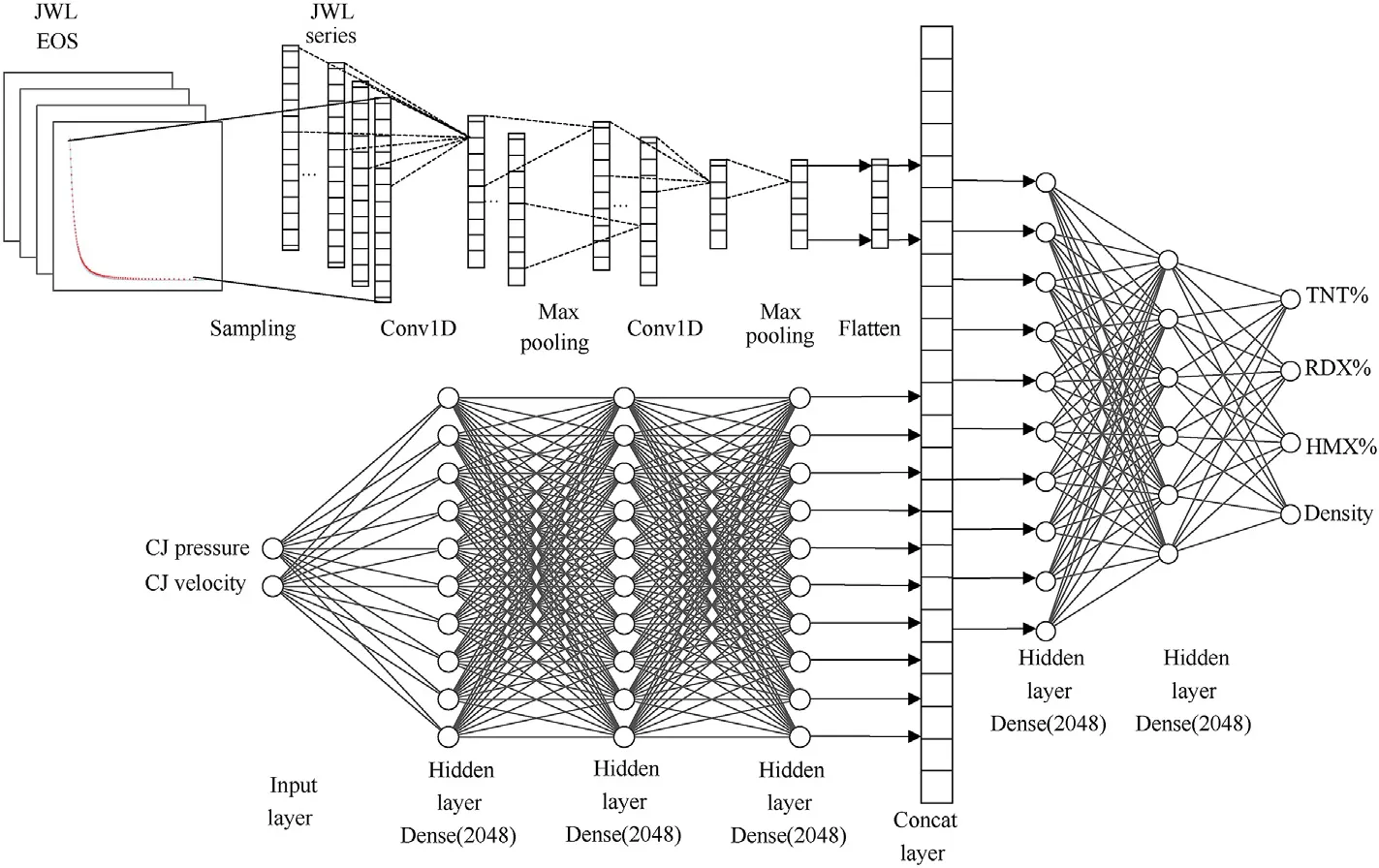
Fig. 5. Schematic of the structure of inverse prediction model.

In this model,the JWL isentropic expansion curve was sampled at a fixed specific volume to obtain a sequence.The sequences were then convoluted and pooled twice. After flattening into a vector through a flattened layer,it can be inputted into the fully connected network for training. However, several other features (detonation pressure and velocity) are also important information for explosives.If convoluted with the JWL curve sequence,the features may be obscured. Therefore, these items were modeled by a fully connected layer. The fully connected layer of detonation parameters and the flattened layer of the JWL curve are connected through a concatenated layer, followed by two hidden layers and an output layer that contains the mass fraction and charge density of the explosive.The training epochs of the inverse model were 1000.

3.3.3. Model validation

The model validation of the inverse prediction was the same as that of the first two models.To judge the fitting effect of the model and whether it is over-fitted, It must be validated through a validation set that is not included in the training set. In the first two models, the data of the LLNL explosive handbook are used for model accuracy validation; however, the LLNL manual only contains the parameters of the JWL equation of state but does not contain the complete JWL isentropic expansion curve.Therefore,it is difficult to test its accuracy, and only the validation-set test is carried out.

4. Result and discussion

4.1. Discussion of detonation parameters prediction model

4.1.1. Model validation set test

The detonation parameters prediction model established in Subsection 3.1 was trained with training data obtained using the KHT thermochemical code. After 1000 epochs of training, the model tended to converge,and it was validated using the validation set data not included in the training set. A comparison of the reference and predicted values is shown in Fig. 6.

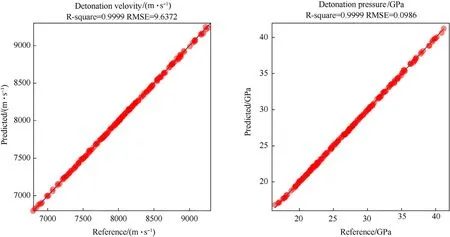
Fig. 6. Comparison of predicted detonation parameters of validation set with the reference values of validation set.

The abscissa in the figure is the reference value,and the ordinate is the predicted value. The closer the predicted point is to the diagonal, the better the fitting effect. The closer the corresponding judgment index(R-square)value is to 1,the better the fitting effect.The closer the RMSE is to 0, the smaller the fitting error. In the fitting of detonation pressure and detonation velocity,theR-square was above 0.99, and the RMSEs were 0.0986 GPa and 9.6372 m/s respectively, and the error between the predicted value and the reference value was within 1%. This indicates that the model also had a good prediction level for the validation set that was not utilized in the training, and few overfittings occurred. Therefore,the detonation parameters of explosives can be predicted with a given formulation.

4.1.2. Model accuracy test

In the validation-set test, it was verified that the prediction model can effectively learn the law between the formulations of explosives and the detonation pressure and detonation velocity in the training set. To validate whether the prediction model can predict the detonation parameters of actual explosives, the prediction must be compared with the reference values of actual explosives.

The trained model was applied to predict the actual explosives with TNT, RDX, and HMX as components, and the results were compared with the explosive detonation parameter values reported in the LLNL explosive handbooks and other literatures[30—33]. Table 1 presents the results.

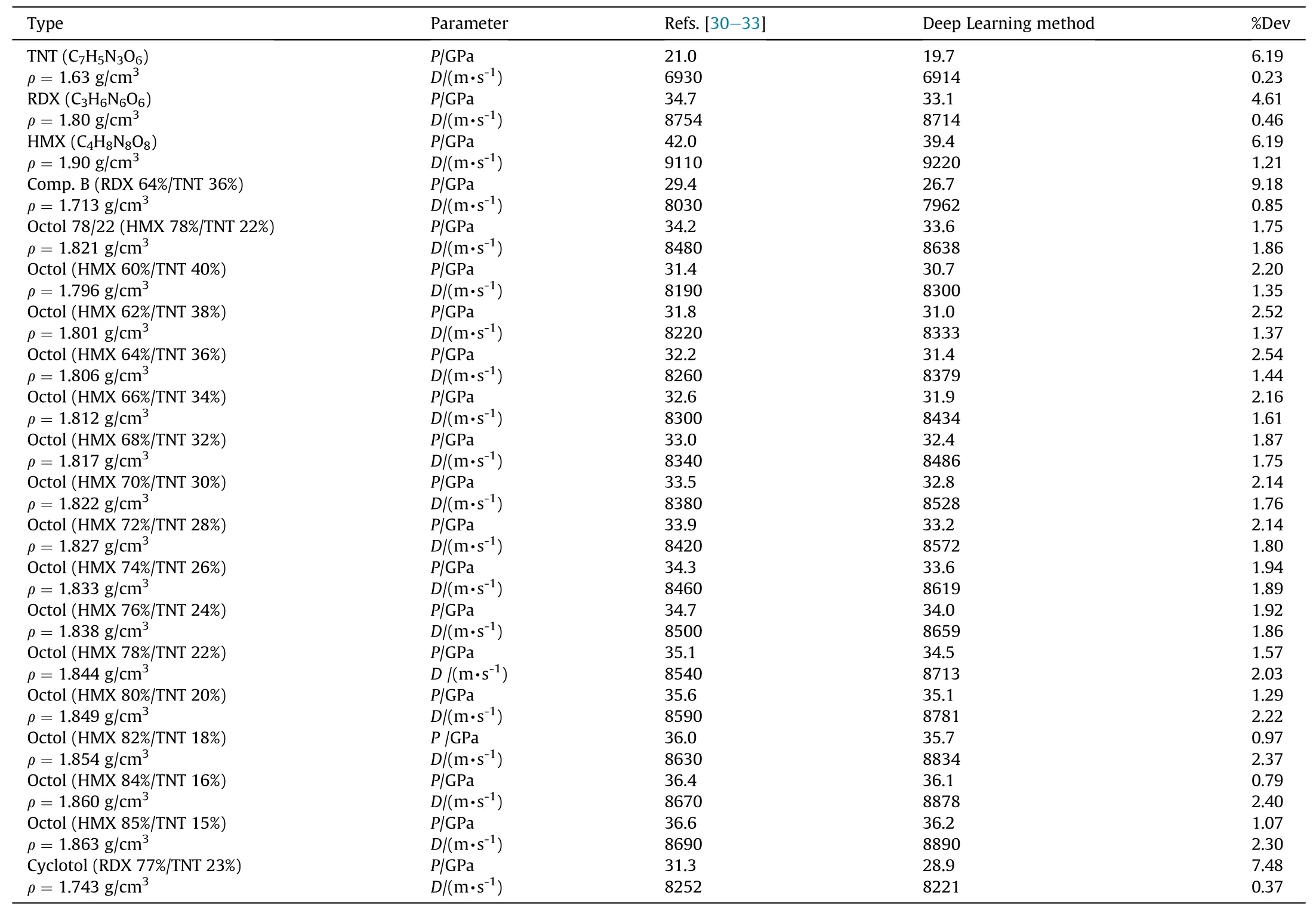
Table 1A comparison of the detonation-parameter reference values with the prediction values by the deep learning model.

From Table 1, it can be observed that for several typical explosives, compared with the reference values in Refs. [30—33], the prediction error of the detonation pressure is less than 10%and the prediction error of the detonation velocity is less than 3% for the formulations consist of TNT/RDX/HMX. This is equivalent to the error in the direct prediction of detonation parameters using the complex thermochemical calculation method [7]. For the prediction of detonation parameters of explosives,the trained prediction model has high accuracy, and can meet the needs of engineering design.

4.2. Discussion of JWL EOS parameters prediction model

4.2.1. Model validation set test

The JWL EOS parameters prediction model was trained using training data obtained from the KHT thermochemical code. The input of the model is the mass fraction of explosives and the charge density,and the output is the JWL equation of state for parametersA,B,R1,R2,C, and ω. After 3000 epochs of training, the model tended to converge. The validation set data (not included in the training set) were used to test the model. A comparison of the reference and predicted values is shown in Fig. 7.

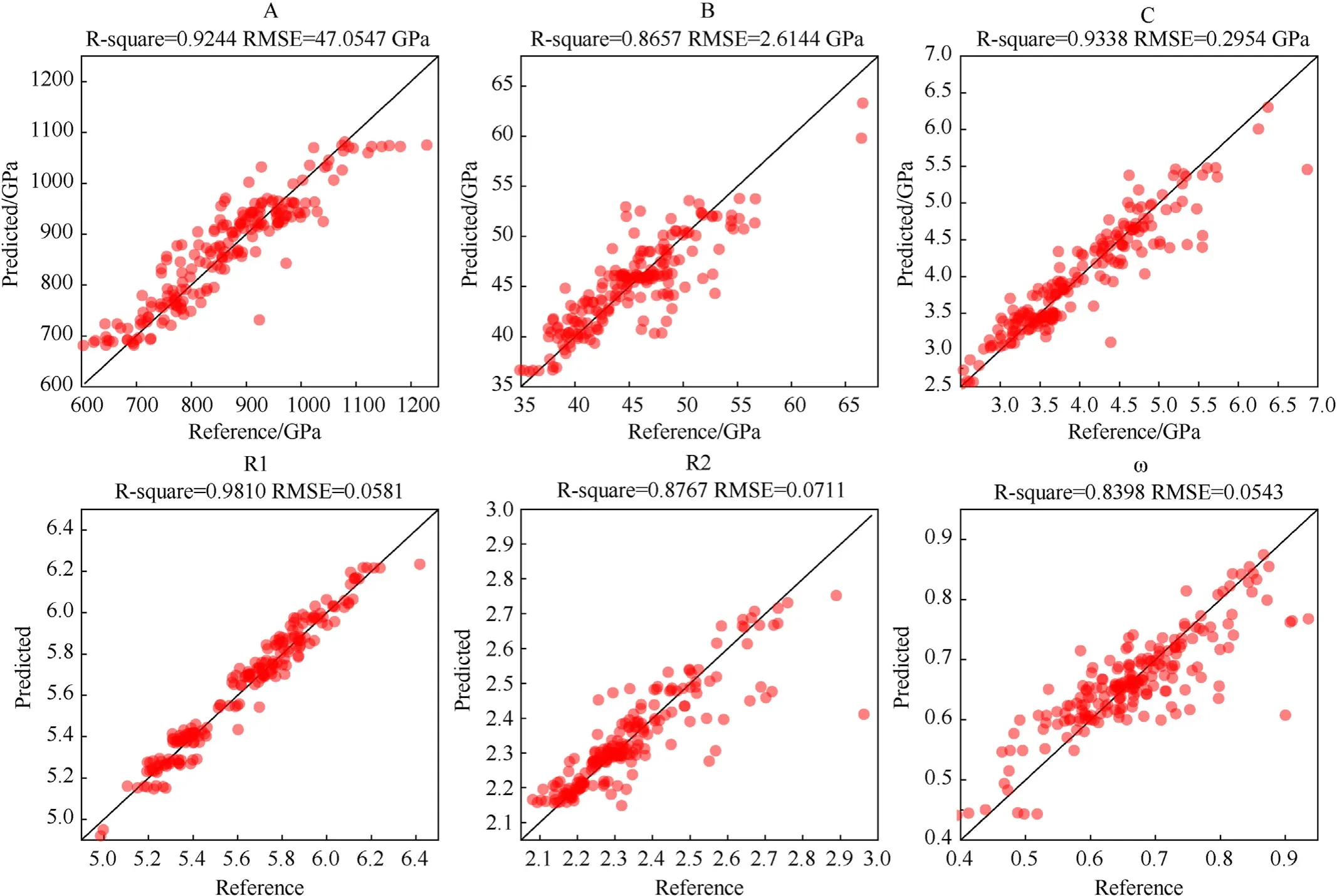
Fig. 7. Comparison of the predicted JWL EOS parameters of the validation set with the reference values of the validation set.

The abscissa in the figure is the reference value and the ordinate is the predicted value. During the establishment of the JWL EOS parameters prediction model,there were six objective functions in total. The model must reduce the loss function values of the six objective functions simultaneously,which complicates the training,and the JWL EOS parameters in the original data are fitted from the isentropic expansion curve data, which have strong nonlinear characteristics. Therefore, the fitting accuracy of the JWL EOS parameters prediction model is not as high as that of the detonation parameters prediction model; however, in the fitting of six parameters,theR-square was above 0.83,and the error of some points was slightly larger.Furthermore,the overall trend was still near the diagonal,indicating that the model also had a good prediction level for the validation set that was not utilized in the training and could accurately predict the JWL EOS parameters with a given mass fraction and charge density.

4.2.2. Model accuracy test

The trained model was applied to predict the JWL EOS parameters of three typical explosives, and the results were compared with the database parameters of the LLNL laboratory.A comparison of the prediction results with the database parameters is shown in Table 2.

Table 2Comparison of JWL EOS parameters by the deep learning model prediction with the reference values.

In Eq.(2),A,B,andCof the six parameters are in the numerator,whereasR1,R2, and ω are in the denominator. Therefore, although the predicted value of the deep learning method is larger than the literature value, when all parameters increase simultaneously, the numerator and denominator increase simultaneously; thus, the isentropic expansion curve points corresponding to the parameters may still be correct. All parameters are larger because the fitting range and initial value of the training data generated by the KHT thermochemical code are different. Therefore, to determine whether the parameters predicted by the deep learning method are correct, the isentropic expansion curve corresponding to the JWL state equation parameters should be compared.The predicted EOS parameters and the EOS parameters in the literature (reference values) were used to plot isentropic expansion curves. A comparison of the isentropic expansion curves of three typical explosives is shown in Fig. 8.

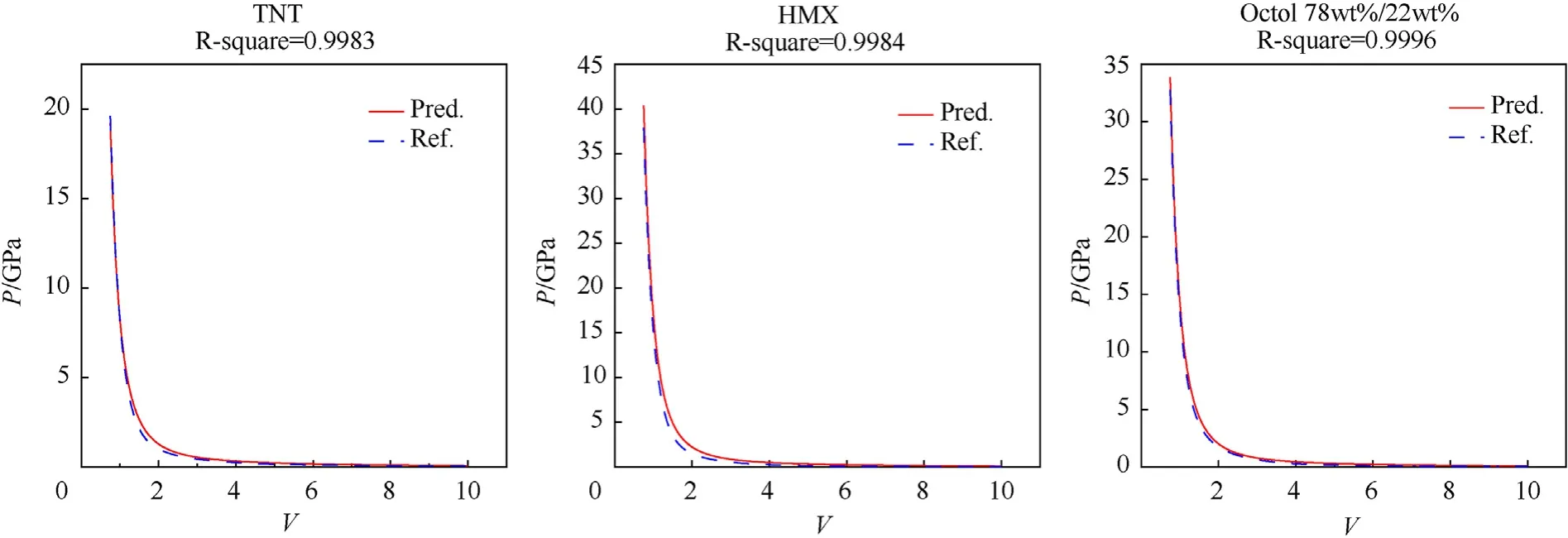
Fig. 8. Comparison of the predicted JWL EOS parameters of three real formulations with the reference value of the validation set in the literature.

TheR-square values of the three explosives were 0.9983,0.9984,and 0.9996, respectively, indicating that the prediction results of the model were good. The predicted JWL EOS parameters are in good agreement with the isentropic expansion curve corresponding to the JWL EOS parameters in the reference LLNL explosives handbook. This shows that although the JWL equation of state parameters predicted by the trained model for the formulations of the input mixed explosives is different from the reference values given in the LLNL manual,the corresponding JWL equation of state curves calculated by the two are consistent.This indicates that the JWL equation of state parameters predicted by the trained model can satisfy the engineering accuracy and engineering design requirements.

4.3. Discussion of inverse prediction model

4.3.1. Model validation set test

The inverse prediction model was trained using training data obtained from the KHT thermochemical code. The input of the model is the detonation parameters of the explosive and isentropic curves of the JWL EOS, and the output is the mass fraction of the explosive and charge density. After 1000 epochs of training, the model tended to converge.Validation set data(not included in the training set) were used to test the model. A comparison between the reference and predicted values is shown in Fig. 9.

Fig. 9. Comparison of the predicted explosive formulations of the validation set with the reference value of validation set.

Fig. 10. Comparison of the predicted explosive formulations with the original formulations.

The abscissa in the figure is the reference value and the ordinate is the predicted value. The predicted point is very close to the diagonal,indicating that the model has barely been overfitted.For the prediction of explosive components, because the sum of the mass fractions of the three explosives is required to be 1, only the mass fractions of the two explosives are independent, and the error of the other is the sum of the first two; therefore, the error of one component will be larger.For the calculation results,the correlation coefficient, R-square, is above 0.99, and the RMSE is around 0.02(i.e., mass fraction 3%). For the prediction of charge density, the correlation coefficient was 0.9983,and the RMSE was 0.0107 g/cm3;thus, the prediction result was relatively accurate.

The data in the training set were all generated using the KHT thermochemical code. To test whether they are applicable to real explosives, the model should be tested using actual explosive formulation data. First, according to the formula of several typical explosives,five typical explosives,namely,TNT(100%TNT,density 1.63 g/cm3),RDX(100%RDX,density 1.80 g/cm3),HMX(100%HMX,density 1.90 g/cm3), Octol 78/22 (22% TNT, 78% HMX, density 1.821 g/cm3),and Comp.B(36%TNT,64%RDX,density 1.713 g/cm3),were taken as calculation examples; their isentropic expansion curves and detonation parameters were calculated by using the KHT thermochemical code. The calculation results were used as inputs to predict the formulations using the trained inverse prediction model (the data of typical explosives were not included in the training and validation sets). A comparison between the predicted and original formulations after the model prediction is shown in Fig.10.

For the five examples of explosives, every two columns in the figure represent a group. The left and right columns represent the reference explosive formulation and predicted formulation,respectively. The latter was predicted by the inverse prediction model with the detonation parameters and the JWL isentropic expansion curve as the input. Different colors show the mass fractions of the three basic explosives in each formulation. The curves in the figure represent the density (right-hand coordinate axis).For the five examples of explosives,the prediction error of the mass fraction was less than 9%, and the prediction error of the charge density was below 1.84%. This shows that the model has a high reverse prediction accuracy,and it can accurately identify the components of explosives from the isentropic expansion curve and detonation parameters. This indicates that the inverse prediction model established in this study can provide guidance for the engineering design of explosives. The model trained in this study is limited to mixed explosives composed of TNT, RDX, and HMX. If other explosives are used as formulations, the inverse prediction model of the corresponding explosives can be obtained by training the model after generating data using similar research methods.

5. Conclusions

Based on two deep learning methods,namely,ANN and CNN1D methods, detonation parameters prediction, JWL EOS parameters prediction, and inverse prediction models were established in this study.The detonation parameters prediction model can predict the detonation parameters of explosives according to the input of explosive formulations.The JWL EOS prediction model can predict the parameters of the JWL equation of state of the explosive according to the input of explosive formulations. The inverse prediction model can predict explosive formulations according to the input of the JWL EOS curve and the detonation parameters. The correctness and low overfitting levels of the three models were verified using a validation set test.Through a model accuracy test,it was verified that the model can meet the engineering accuracy requirements. The model established in this study can achieve rapid and large-scale predictions of explosive properties. Weapon designers can predict explosive properties by inputting explosive formulations, without mastering the complex thermodynamic calculation process. The inverse prediction model can enable warhead designers to directly design explosive formulations according to their detonation property requirements,which has great engineering significance.

For the model established in this study,only TNT,RDX,and HMX were used as basic explosives. This is because these three traditional explosives are widely used in warheads, and the trained model results are only valid for explosive formulations consisting of these three basic explosives. For the prediction of new explosives and formulations, the training data of explosives with new compositions can be obtained using the KHT code. The detonation parameters and JWL EOS parameters can be predicted or inversely predicted using the training data for the model.In future work,the inverse prediction model established in this study can be used for engineering research on explosive formulation designs. By adding control items such as explosive cost, explosive safety, and other factors, the explosive formulation can be jointly optimized using the established model and other intelligent algorithms, which can provide better guidance for warhead design.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.