Region coverage control for multiple stratospheric airships with combined self-/event-triggered mechanism

Yi-fei Zhng , Ming Zhu , Tin Chen , Ze-wei Zheng

a School of Aeronautic Science and Engineering, Beihang University, Beijing,100191, China

b Institute of Unmanned System, Beihang University, Beijing,100191, China

c School of Electronic and Information Engineering, Beihang University, Beijing,100191, China

d School of Automation Science and Electrical Engineering, Beihang University, Beijing,100191, China

Keywords:Formation coverage control Combined self-/event-triggered control Improved artificial potential field

ABSTRACT

1. Introduction

The control problem of the stratospheric airship has become a hot research topic, as the stratospheric airship has unique advantages in performing continuous high-attitude air-to-ground tasks,such as early warning, reconnaissance surveillance, area monitoring, communication relay and so forth, thanks to its aerostat characteristics [1]. Several control problems like path following[2,3], trajectory tracking [4—6], and station keeping [7—12], have been addressed for the control of the single stratospheric airship.As the cost of the stratospheric airship is far less than that of other types of aerial vehicles, developing multiple stratospheric airships(MSAs)system[13]has become a future trend.Moreover,the MSAS system can also broaden coverage and enhance application functions compared to the single stratospheric airship.

Recently,many researchers have put their research focus on the formation control of MSAs system [14—16] due to its promising future in the application. To cite examples, in Ref. [14], a flexible formation control method based on path following and leaderfollower structure is proposed. Approximation-based local adaptive tracking controller is designed in Ref. [15] with eventtriggering law. A distributed fractional-order fault-tolerant formation-containment control scheme is proposed in Ref. [16].However, the aforementioned works only solve the formation control problem with a specified formation pattern,which does not conform to the practical characters and application scenarios of the MSAs system.

The practical characters and application scenarios of the MSAs system,different from traditional multiple UAVs system,inspire our research in this paper. First of all, the external wind speed is the same order as the flight speed of the stratospheric airship [17], so the formation control based on specific formation patterns is difficult to achieve in practice. Furtherly, considering of platform advantage that being able to perform long-time station keeping,region coverage is the main application mission scenario of the MSAs system [18]. Moreover, as a long-duration platform,communication bandwidth and computing resources are usually physically limited[19],which should be considered in the solution to the formation control problem of the MSAs system. To summarize, problems of formation control and coverage control have to be combined as the formation coverage control problem,which is worth investigating for the MSAs system.

In most research works,the formation coverage control problem is deemed as a locational optimization problem[20—30]where the main objective is the optimal placement of mobile robots to cover a given domain. Solutions in these works are not matched to the formation coverage control problem of the MSAs system.One of the reasons is the complex calculation of locational optimization,which makes it difficult to realize real-time guidance and control of MSAs system. To cite examples, in Ref. [23],off-line reinforcement learning and a γ-information map are used together to cope with area coverage problem for the multi-agent system. The timeoptimal Voronoi partition is developed by using the optimal control theory and Lloyd's algorithms to minimize the designed cost function evaluating the performance of the coverage network in Ref. [26] without consideration of trajectory tracking control. The formation coverage control law in Ref.[30]is designed to minimize a complex coverage cost function which is defined to be the largest arrival time from the mobile sensor network to the points on a circle.Another one is that most of the given domains designed to be covered in Refs. [20—30] are unpractical simple, such as straight line [27,29], circle [22,25,30], closed curve [21], rectangle area[20,24] and so forth. In contrast, the practical demands of the formation coverage control law including computationally efficient guidance law as well as irregularity of coverage region shape are all considered in this paper.

Besides, another control problem that is closely related to formation coverage control is persistent surveillance and monitoring[31—35], where the repetitive motion of the aerial vehicles is required. Unlike them, the formation coverage control problem of MSAs system is to design a mission-oriented formation controller to realize station-keeping control [7—12] for a group of stratospheric airships, which is likely to large-scale positioning control problem in Ref. [36] as repetitive regular motion is unnecessary.

Based on all the above considerations, the APF method is introduced as a computationally efficient guidance scheme in this paper.The main advantage of the APF method is its low calculation cost,even with complex potential functions.In Ref.[37],Khatib has already proven that the APF method is simple but effective to realize obstacle avoidance and collision avoidance in robotic systems, while attraction and repulsion potential functions for stable formation control have been discussed in Ref.[38].Usually,the APF method is widely used in path planning for mobile robots [36,39],mobile vehicles [40—42], UAVs [43], USVs [44] and satellites[45,46],but the dynamics and kinematics of controlled objects are not considered in these research works. Considering the practical application, dynamics and kinematics of the stratospheric airship should be considered in the formation coverage control with the application of the APF method.

In the application of the APF method, local minimum [47] is worth to be taken seriously,especially when the shape of the region is prepared to be designed as irregular.In Refs.[48,49],the clusters of high-likelihood for the existence of an obstacle are designed to be responded to in the designed controllers, aiming at ignoring local minimum. The application of these two methods is limited due to their dependence on the ability of sensors. Bacterial evolutionary algorithm(BEA)is combined with the APF method to cope with the problem of local minimum [50], planning an optimal escape path according to the designer's criteria.The disadvantage is that its calculation cost is unacceptably high when the dynamics and kinematics are considered. Besides, control schemes in Refs. [48—50] are designed merely based on the applicative scenario of a standard U-shape obstacle, not an irregular-shape obstacle. In this paper, the influence of local minimum for irregular-shape forbidden-region,which is kind of like an obstacle,is properly minimized by a designed novel virtual control law with the help of event-triggered control technology.

In traditional engineering applications, the periodic transmission of state information, update of control input, and other operations, result in unnecessary resources consumption. The aforementioned event-triggered control technology is an effective and well-researched tool that focuses on reducing the communication and calculation resources consumption while ensuring satisfactory control performances in the formation control. As event-triggered control technology has been a subject of interest in the formation control[51—54]because of the efficient management of control signals with limited network resources, introducing event-triggered control technology into formation coverage control is suitable for MSAs system with the consideration of sources saving.

Motivated by all the above discussions, this paper considers a more practical control framework to solve the region coverage formation control problem of MSAs. Considering the practical characters and application scenarios of the MSAs system aforementioned, the main contributions lie in the following aspects:

(1) The region coverage control problem of the MSAs system is firstly investigated in this paper, considering stratospheric airship's practical characters and several practical control problems such as unknown individual differences, external disturbances, and resource constraints of communication and calculation. Moreover, several practical application scenarios such as the existence of a forbidden region and shortness of released stratospheric airships are also considered.

(2) Compared with [39—43,45,55], the APF method is properly utilized to design virtual control lawsandto help achieve the aim of region coverage mission. Besides, the designs of virtual control lawsandalso have the ability of giving an escape yaw velocity and an escape yaw angle to avoid local minimum when MSAs member reaches where near local minimum.More importantly,an APF-based self-triggered mechanism is firstly designed in this paper,satisfying the aims of giving escape time to help avoid local minimum and avoiding continuous communication to save communication resources.

(3) Compared with [20—30], the dynamics and kinetics of the controlled object are all considered.A novel NN-based eventtriggered adaptive controller is designed to track the desired velocity and angular velocity with the effect of solving the problems of unknown individual differences and external disturbances. The event-triggered mechanism designed therein can effectively reduce the times of control law calculation to save calculation resources.

The rest of this paper is organized as follows. In Section 2, the preliminaries are provided. In Section 3, a region coverage control scheme for the MSAs system is proposed with the consideration of unknown individual differences, external disturbances, and resources saving, while mathematical proofs of Lyapunov stability and the exclusion of Zeno behavior are given. In Section 4, simulations are performed to demonstrate the effectiveness of the proposed method. Finally, Conclusions are provided in Section 5.

2. Preliminaries

2.1. System description

Assumption 2.1.The stratospheric airships are all rigid bodies,thus the aeroelastic effects of airships can be ignored.

Referring to Ref.[56],the kinematics and dynamics of memberiof MSAs can be expressed as

where ζi=[χi,ψi］Tdenotes the vector of position χi=[xi,yi］Tand yaw angle ψi,Jidenotes coordinate transform matrix defined as Eq.(2) and Eq. (3), Θi=|Θp,i,Θa,i|Tdenotes the vector of velocities Θp,i=[ui,vi］Tand yaw angle velocity Θa,i,MiNidenotes the vector of aerodynamic forces and torque, fidenotes unknown forces and torque generated by unknown individual difference,τidenotes the control vector, and didenotes the vector of external disturbances.Remark 2.1.As the stratospheric airship is a kind of aerostat with a gondola fixed under its envelope,implying its center of gravity is rather lower than its center of the body. Therefore, of most stratospheric airships, the height is almost unchanged because of the dynamic balance of gravitation and buoyancy, while the roll angle and the pitch angle are self-stable because of its inverted pendulum-like mass distribution characteristics. Moreover, the inertia and added inertia of the stratospheric airship is large because of its large bulk,the height,roll angle,and pitch angle are usually designed as uncontrollable in most overall designs. Therefore,height, roll-angle, and pitch-angle control are all ignored.

Assumption 2.2.In practical scenarios,the external disturbances diand unknown forces/torque fiare unknown but bounded vectors.Mathematically,there exist positive real numbersthat satisfy

2.2. APF method

APF method is utilized to guide MSAs to fulfill the mission of region coverage.In this paper,the resultant artificial potential field is composed of several different artificial potential fields denoted as subAPFs. For each particular subAPF, the potential function is defined asPk, then the potential force can be obtained as Fk=grad（Pk）.

Thus,for the resultant potential fieldPconsisting ofnsubAPFs,the resultant potential force can be obtained as (see Fig. 1) F =Σnk=1grad（Pk）.

2.3. Control objective

The objective of this paper is to design a formation coverage control scheme for the MSAs system to achieve the mission of region coverage. As shown in Fig. 2, the mission can be depicted as follows: several stratospheric airships are controlled to start from the release region, bypass the forbidden region, reach the target region and fully cover the target region to perform specific region coverage tasks.

Fig. 2. Depiction of region-coverage mission.

Specifically,the objectives of the designed control scheme are as follows:

(1) Potential functions (PFs) for several subAPFs are designed

based on the demands of the coverage mission;

(3) Influence of unknown individual differences and external disturbances can be eliminated by the control scheme;

(4) Times of state information transmission and control law calculation can be reduced by the control scheme.

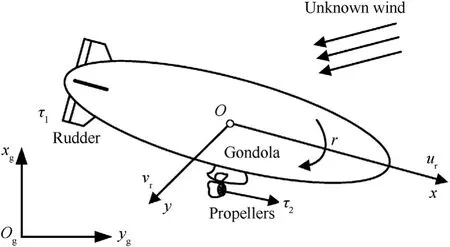
Fig.1. Structure of the stratospheric airship.

3. Controller design

As shown in Fig. 3, the main results of controller design are presented in this section. To meet the control objective, the proposed method is divided into four parts:region-coverage missionoriented artificial potential field,a self-triggered APF-based virtual control law, an event-triggered adaptive formation coverage controller,and stability analyses.In the first part,the APF method is introduced to provide a guidance method to guide airships to achieve the mission of region coverage,by the means of designing PFs to make sure the global minimum point of the resultant potential field is the target station-keeping point for every single airship. In the second part, virtual control lawsandare designed to meet the aim of minimizing the resultant potential fieldPto global minimum and avoiding local minimum, with the help of a designed self-triggered mechanism. In the third part, to eliminate the influence of individual difference and external disturbances,an NN-based adaptive controller τiis designed to reduce the tracking error ξΘ,ito a small neighborhood of zero while an event-triggered mechanism is designed therein.In the fourth part,rigorous theoretical analysis for the Lyapunov stability of the whole closed-loop system and the exclusion of Zeno behavior is provided.

Fig. 3. Block Diagram of the region coverage control for MSAs member i.

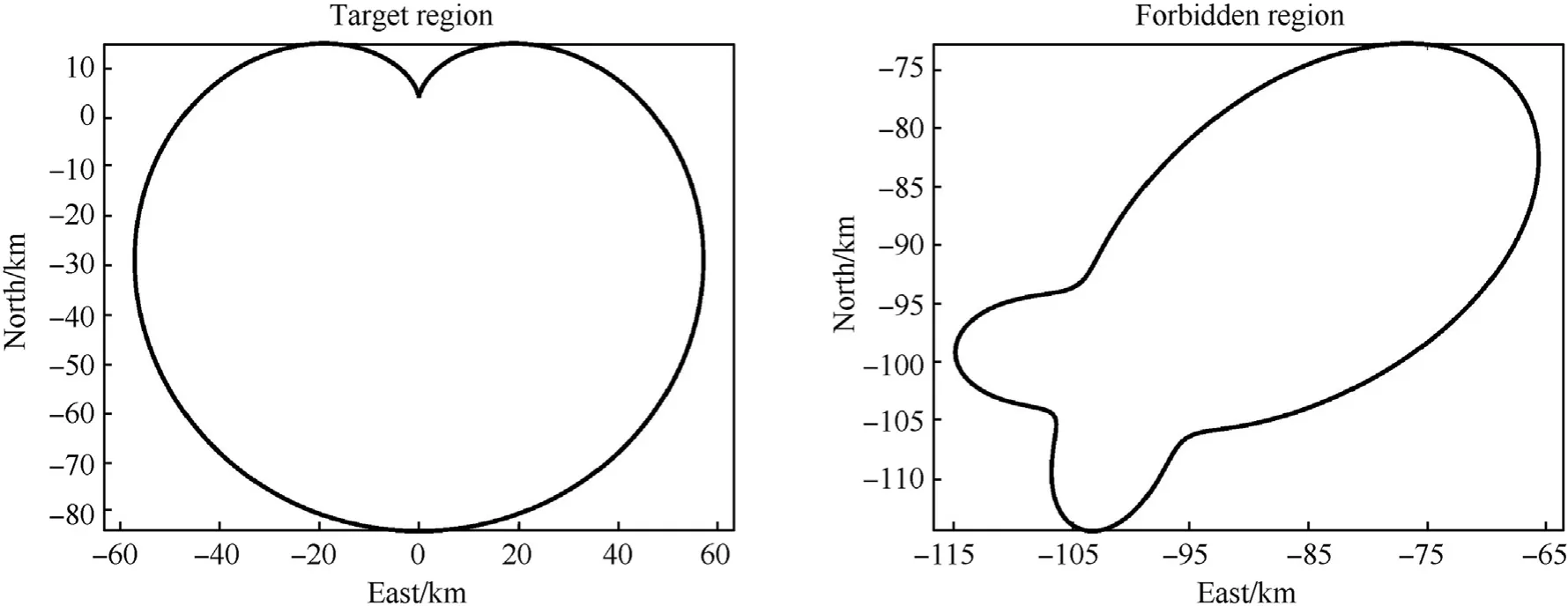
Fig. 4. Target region and forbidden region.

Fig. 5. Region artificial potential field.

3.1. APF design

The designed APF is consist of four subAPFs as follows:a region attractive subAPF denoted asfor target region to guide airships to reach the target region, a mutual repulsive subAPF denoted asto guide airships to fully cover the target region and a region repulsive subAPF denoted asfor the forbidden region to guide airships to avoid the forbidden region.In addition,considering the scenario that the number of released airships is short to fully cover the target region, a mutual attractive subAPF denoted asPam,ito guide airships to cover part of the target region compactly and effectively. Above four subAPFs are designed in subsections 3.1.1-3.1.4, and the irregular-shape extension of the coverage region is given in Subsection 3.1.5.

3.1.1. Region attractive subAPF

Define the relative distance as

whereRais the radius of the target region. And the corresponding potential force can be gotten as

3.1.2. Mutual repulsive subAPF

For airship memberi, dij=χi-χjis the distance away from airship memberjas χjdenotes the position of airship memberj,andis the desired relative distance betweeniandj,then the mutual repulsive potential field ofjforiis designed as

And the corresponding potential force can be obtained as

The total mutual repulsive subAPFforiis

And the total mutual artificial repulsive force is

3.1.3. Region repulsive subAPF

The center of the forbidden region is defined as χr=[xr,yr］Tand the relative distance for airship memberiaway from it isχr, then the artificial repulsive potential filedfor memberiis designed as

whereRris the radius of the forbidden region, and the corresponding artificial repulsive force is

3.1.4. Mutual attractive subAPF

The mutual attractive potential fieldPam,iofjforiis designed as

and the corresponding artificial attractive force is

The total mutual attractive subAPFforiis

and the total mutual artificial attractive force is

Remark 3.1.It can be proved that potential fields andall are linear and differentiable.

3.1.5. Extended artificial potentialfield

In Ref. [37—43,45,55], the shapes of APFs are all circle-like.Considering that in most practical application scenarios, the shapes of the region are not all circle-like.In this paper,the shapes of the target region and forbidden region are all extended to any irregular shapes which can be expressed as a polar coordinate system.As shown in Fig.4,the target region is defined as a heart-shape region whose center is（0 km,0 km）and polar radius isRa=40｛1 -cos[π -arctan］｝（km）,and the forbidden region is defined as an airship-shape region whose center is （-10 km,-10 km） and polar radius isRr= 8｛1 ＋ 2cos2[1˙3π ＋ arctan＋ 2cos2[1˙3π ＋arctan＋cos[1˙3π ＋arctan（km）.In Fig.5,the region APF is formed based on Eq.(12)and Eq.(14),while the artificial potential is highest in the forbidden region and is lowest in the target region,which means that this designed region APF will guide airships to the target region with the avoidance of the forbidden region.

Besides, in Fig. 6, the mutual artificial potential field of airship memberjforiis formed based on Eq. (12) and Eq. (14), while the artificial potential is highest wheniis at the same point ofjand is lowest wheniandjkeep a predefined relative distance, which means that this designed mutual APF will guide airship memberito keep a relative distance from airship memberj. Airship-to-airship relative distance is related to the coverage ability of the single airship.

Fig. 6. Mutual artificial potential field.

3.2. Self-triggered virtual control law design

Based on the designed APF, the virtual position control law Eq.(18) is designed to generate the desired velocity for memberi.wherekp,kr,a,kr,r,km,a,km,r∈R＋and positive vector all are control parameters.

The tracking error of the current yaw angle is defined as ξa,i=ψi- arctanBased on Eq. (18), the virtual yaw-angle control law is designed as

wherekψ∈R＋is a chosen control parameter.

Remark 3.2.In Eq. (18), an APF-based self-triggered control mechanism will be designed andis the triggering instant at which communication devices on the memberirequest and receive the position information of other members. At the same time, the virtual control law is calculated and the desired velocity and the desired angular velocities are generated for the next-step controller. As the avoidance of unnecessary communication, the purpose that saving communication resources is achieved.

To design this self-triggered control mechanism, the measurement error Eq. (20) representing the dynamic error of potential force is designed firstly.

Then triggering Eq. (21) is designed to define certain instants that the virtual control law is decided to be triggered,at the time of φP,i,λ（t）≥0,∀λ = 1,2.

where positive real vector ϖ1=diagwith ϖ1˙λ∈（0,1）is the triggering control parameter. Simultaneously and similarly,ϖ2>0.

To practically save communication resources by reducing state information transmission times, periodical calculations of triggering function have to be avoided.In the next step,a self-triggered mechanism is going to be designed based on the triggering Eq.(21).

To denote the changing rate of potential force error, the derivative of Eq. (20) under the limit of triggering function Eq. (21) is derived for ∀λ=1,2 as Eq. (22).

Integrate Eq. (23) to obtain the inequality related toas

Remark 3.3.The design of virtual control laws Eq. (18)- Eq. (19)and self-triggered mechanism Eq. (25) can effectively avoid local minimum.When a certain MSAs member comes into the occasion of the local minimum in which the total potential forcereaches the local minimum, the effect of ϖ2will be locally maximized, then the designed virtual control laws will generate the desired escape velocity and the desired escape yaw angle,while the designed self-triggered mechanism (25) will generate an escape time to help this MSAs member to escape from the local minimum.As Fig. 7 is given to explain the effectiveness of the designed method, when a certain MSAs member reaches somewhere near the point of local minimum,the desired yaw angle will be deviated as the escape yaw angle, while escape velocity given by virtual control lawand escape time given by self-triggered mechanism(25), this MSAs member would never arrive at the point of local minimum.

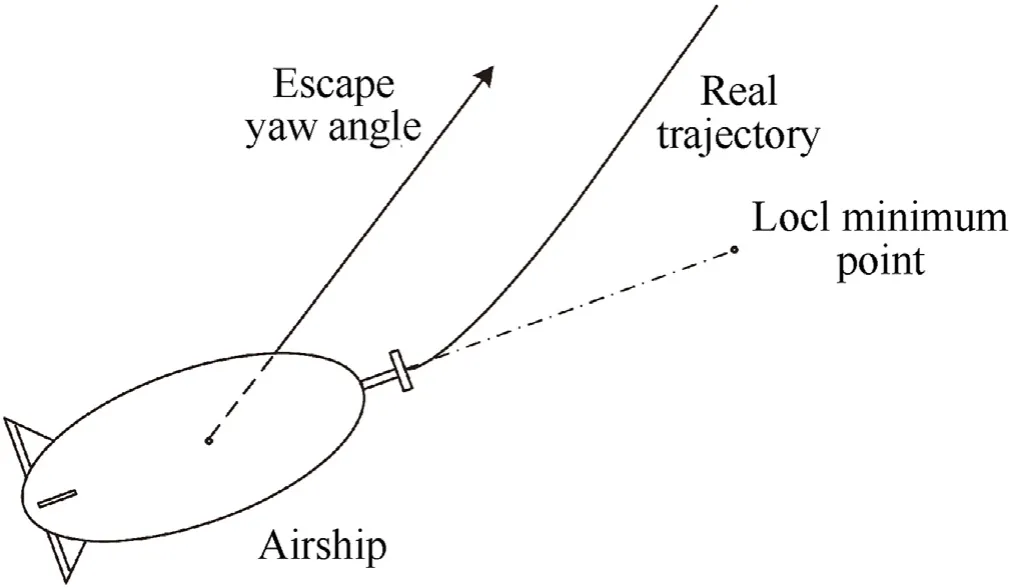
Fig. 7. Depiction of local minimum avoidance.

Consider a Lyapunov candidate

Its derivative can be obtained as

where γ>0.

Consider another Lyapunov candidate

Its derivative can be obtained as

3.3. Event-triggered tracking controller design

Define the tracking error of the desired velocity/angular velocity and the real velocity/angular velocity

Differentiate it as

To estimate unknown nonlinear dynamics caused by unknown individual differences, a neural network is utilized as

where Wiis optimal weighting vector,is the radial basis function vector,and εiis the bounded estimation error as

Then Eq. (31) can be expanded as

where dtotal,i=is the nominal disturbance.

Remark 3.4.The estimate errorof the second-order filter is bounded in a small neighborhood of zero [57]. Derived from Assumption 2.1 and Eq. (32), diand εiare all bounded. Therefore,dtotal,iis a bounded vector satisfyingAn adaptive law is designed with positive parameters α1and β1as

To deal with nominal disturbance, another adaptive law is designed as

where positive matrices α2,β2∈R3×3are adaptation parameters.

Considering the event-triggered control law designed afterward, the controller is designed as

where positive matrices KΘ, Kd, ϖ3, ϖ4∈R3×3all are controller parameters.

Remark 3.5.The event-triggered mechanism, not the selftriggered mechanism, is designed in this tracking controller with the consideration of effective sources saving.The reason is that the self-triggered mechanism has more triggering instants than that of the event-triggered mechanism,which can be proved in Section 4.

The measurement error for this event-triggered control law is defined asThe corresponding triggering function is designed as

where positive real vector ϖ3=diag■ϖ3,1,ϖ3,2■with ϖ3˙λ∈（0,1）is the triggering control parameter. Simultaneously and similarly,ϖ4>0.

Determined by Eq. (38), the triggering time of this eventtriggered mechanism can be obtained as

wherek=0,1,2,3,… and ∀λ = 1,2,3.

Consider a Lyapunov candidate

Its derivative can be obtained as

3.4. Stability analysis

Theorem 1.Consider the stratospheric airship model(1),ifAssumptions 2.1-2.2are satisfied,and under the effect of the designed control scheme with suitable controller parameters,then the errorξΘ,i is guaranteed to be reduced to a small neighborhood around zero so that every single stratospheric airship will reach the global potential minimum point,which means MSAs will be guided to avoid the forbidden region,then reach and fully cover the target region.

Proof. Consider a Lyapunov candidate as

ApplyEq.(27),Eq.(29),andEq.(40),the derivative ofEq.(41)can be obtained as

where

Therefore,the resultant APF,the tracking errorsξa,i, ξΘ,i and theestimation errorsWi are all bounded and can ultimately convergeto the compact setswith appropriate control parameters.

Theorem2Zeno behavior is excluded in the designed combined self-/event-triggered mechanism.

Remark 3.6.For the designed event-triggered or self-triggered mechanism,Zeno behavior denotes that the designed triggered function is constantly satisfied,which means in afinite time there are infinitely many triggering instants.Zeno behavior is physically impossible to realize,which cannot be satisfied in practice.Moreover,Zeno behavior is against the original intention of reducing the number of triggered times.

proof.For the designed self-triggered mechanism, the proof of exclusion of Zeno behavior can be divided into two steps asStep 1-Step 2. In the first step, the designed self-triggered mechanism satisfies the constraint that the triggering function φP,i（t）≥0. In the second step, Zeno behavior is excluded in the designed selftriggered mechanism

Step 1:Based onEq. (24),the inequality holds for∀λ=1,2as

In the meantime,derived fromEq. (25),

To prove that the designed self-triggered mechanism satisfies the constraint that the triggering functionφP,i,λ（t）≥0,an inequality should hold for∀λ = 1,2.

As applyingEq. (23)intoEq. (21)yields

The inequalityEq.(45)holds for∀λ =1,2,thus the inequalityEq.(43)holds for∀λ =1,2.It also proves that the triggering condition of the self-triggered mechanism is stricter than that of the eventtriggered mechanism.

Step 2:ApplyingEq. (21)intoEq. (24)yields

Then,it is obtained as

Zeno behavior is excluded in the designed self-triggeredmechanism.For the designed event-triggered mechanism inSection 3,theproofis given inStep 3.

Step 3:As decided by triggering functionEq. (38),the inequality holds as

For ∀λ = 1,2,3.

Differentiating it as

Obviously, ∃κ3≥0,

Therefore,for∀k,k= 1,2,3,…,

According to the definition of event-triggering functionEq. (38),the inequality is obtained as follows.

Therefore,

For ∀λ = 1,2,3.

Derived fromStep 1- Step 3,Zeno behavior is excluded in the designed combined self-/event-triggered mechanism.

4. Simulation results

In this section,the numerical simulation results are presented to demonstrate the effectiveness of the designed method.

The main model parameters are presented in Table 1. More practically,the limits of control forces and control torque are given in Table 2.

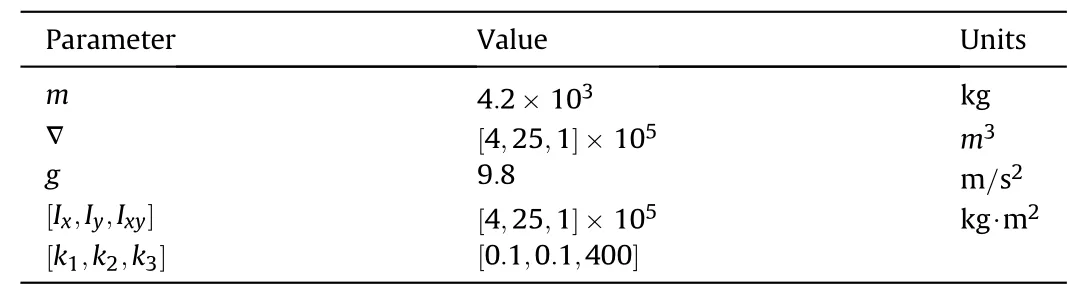
Table 1Model parameters.

Table 2Limits of control forces and control torque.

It is assumed that the target region is a heart-shape region whose center coordinate is （0 km,0 km） and polar radius isRa=（km）, and the forbidden region is an airshipshape region whose center coordinate is （-10 km, -10 km） and polar radius isRr=8｛2cos7[1˙3π ＋arctan＋2cos2[1˙3π＋arctan＋1）｝（km） as defined in subsection 3.1.5. The coverage mission is to be performed by an MSAs system consisting of seven stratospheric airships. The initial positions of MSAs system are set as χ1=[-150 km, -150˙3 km］T,χ2= [-150 km, -150˙6 km］T, χ3= [-150 km, -150˙9 km］T,χ4= [-150 km,-151˙2 km］Τ, χ5= [-150˙3 km, -150 km］T,χ6= [-150˙6 km, -150 km］T, χ7=[-150˙9 km, -150 km］Tand the initial yaw angle of MSAS system are all set as 0◦. The coverage zone of a stratospheric airship is assumed to be the circle with its center at the stratospheric airship's position and the radius is 30 km. The coverage area of the target region is mathematically matched to the total coverage ability of this MSAs system. The external disturbances are set as di=[400＋200di,r（N）,50＋100di,r（N）,1000＋1000di,r（N∙m）］Τwithdi,r=0˙3sin（t／120）＋0˙5 cos（t／360）. The sampling period for monitoring the combinedtriggering conditions is 0.005 s. To indicate the individual difference among different stratospheric airship, the volume, mass, and inertia of different stratospheric airships are different as ∇i= （1＋0˙1i）∇,mi= （1＋0˙1i）m,Ix,i=（1＋0˙1i）Ix,Iy,i=（1＋0˙1i）IyandIxy,i=（1＋0˙1i）Ixy. Because the differences are unknown so thatmi=m,Ix,i=Ix,Iy,i=IyandIxy,i=Ixyin the designed controller.Abovem,Ix,IyandIxycan be obtained from Table 1.

Remark 4.1.From the aspect of practical engineering, to guarantee different stratospheric airships to keep at the same height for the sake of performing collaborative tasks, the variation of the volume has to keep pace with that of the mass for the consideration of the balance of the buoyancy and gravitation. However, the influence of individual differences still exists as these differences are unknown for the designed controller.

The control parameters for virtual control law are chosen askp=0˙3,kr,a= 1× 10-8,kr,r= 1× 1010,km,a= 1× 1020,km,r= 2×10-15,kψ= 3, ϖ1= diag｛0˙3,0˙3｝, ϖ2= diag｛0˙1,0˙1｝. The control parameters for controller are chosen as α1=0˙05,β1=5,α2=diag｛5,5,2｝×10-8,β2=diag｛5,5,8｝×106,KΘ=diag｛1˙2,1˙2,5｝×10-3,Kd=×10-4,ϖ3=diag｛0˙95,0˙95,0˙005｝,

The trajectories of the MSAs system are shown in Fig. 8.Stratospheric airships are released and set off from the blastoff region, then they fly towards the target region with the safety distance for collision avoidance.Fig.8 illustrates that stratospheric airships can successfully bypass the irregular-shape forbidden region with the avoidance of the local minimum shown in partial enlarged detail. Finally, the stratospheric airships reach the target region and perform station keeping on their stable coverage positions while the overall coverage zone fully covers the target region.

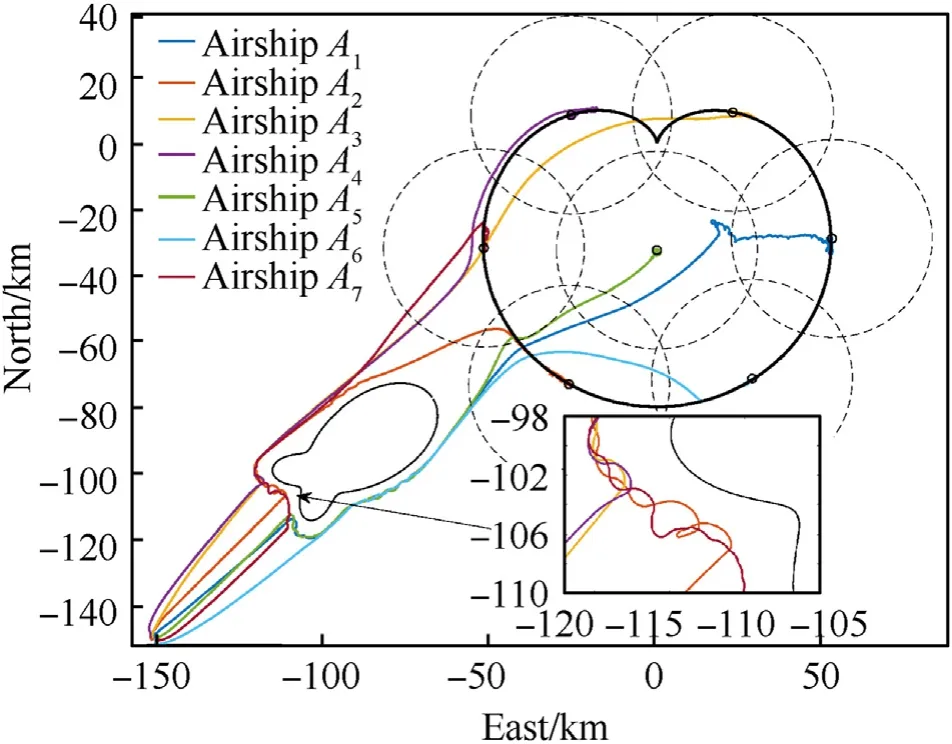
Fig.8. Trajectories of MSAs system and locations of target region and forbidden region.

Fig. 9 and Fig.10 show partial triggering instants of data information transmission,while Fig.11 and Fig.12 show that of control law calculation,proving the effectiveness of the designed combined self-/event-triggered mechanism. Besides, Fig.13 shows that more than 85%of the transmission times of the state information and the calculation times of control law are saved.

Fig. 9. Self-triggered data transmission instants in former 200 s.

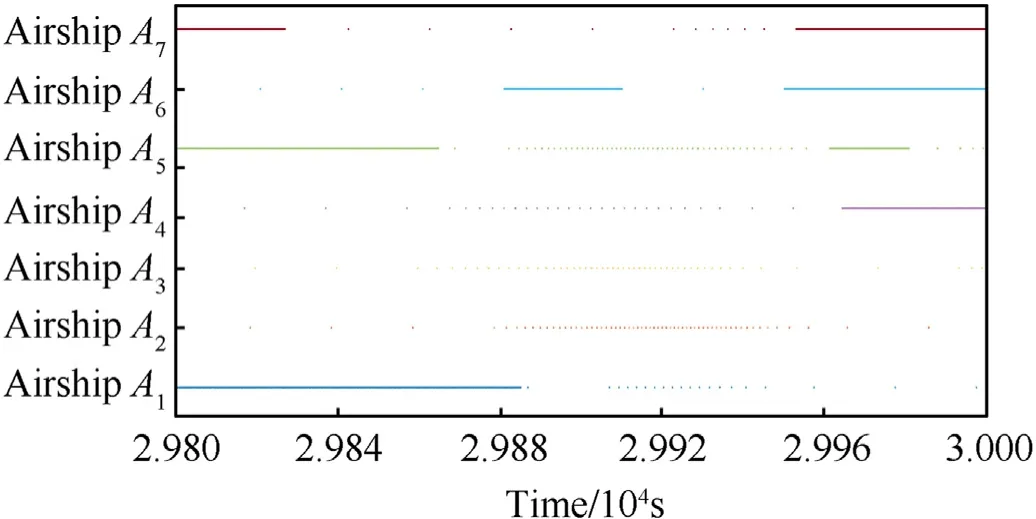
Fig.10. Self-triggered data transmission instants in latter 200 s.

Fig.11. Event-triggered control law computation instants in former 200 s.

Fig.12. Event-triggered Control Law Calculation Instants in Latter 200 s.

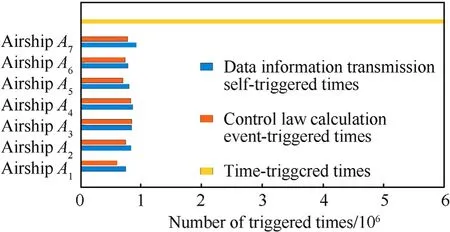
Fig. 13. The contrast of number of triggering times between combined self-/eventtriggered mechanism and time-triggered mechanism.

Without loss of generality, as shown in that Fig.14- Fig.16, the simulation results of MSAs system memberA7are given as an example to demonstrate the effectiveness of the proposed control scheme. Fig.14 shows the control inputs, while the outputs of the adaptive law are shown in Fig. 15 and the outputs of neural networks are shown in Fig.16, they are all bounded, converged, and reasonable.

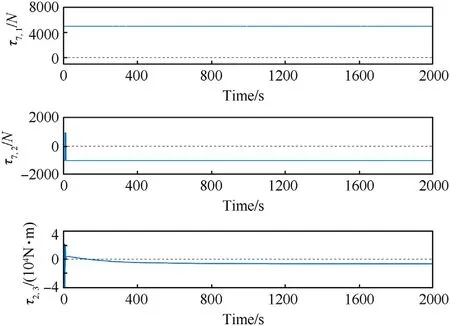
Fig.14. Control inputs of airship A7.

Fig.15. W7TΩ7, The Outputs of neural networks of airship A7.

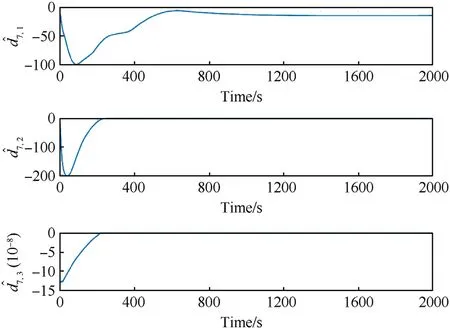
Fig.16. ^d7, The outputs of adaptive law of airship A7.

To clarify the comparison with[20—30],as illustrated in Fig.17,if the dynamics and kinematics model are not considered, the trajectories of MSAs system will be smoother but not practical.However, in this paper, the dynamics and kinematics of the controlled object are considered to make the research more practical and more meaningful.Moreover,based on the consideration of the dynamics and kinematics model, several practical problems such as unknown individual differences and external disturbances can be and are considered in the region coverage control problem of MSAs system. Therefore, compared with [20—30], the proposed method in our paper is more practical and more meaningful.

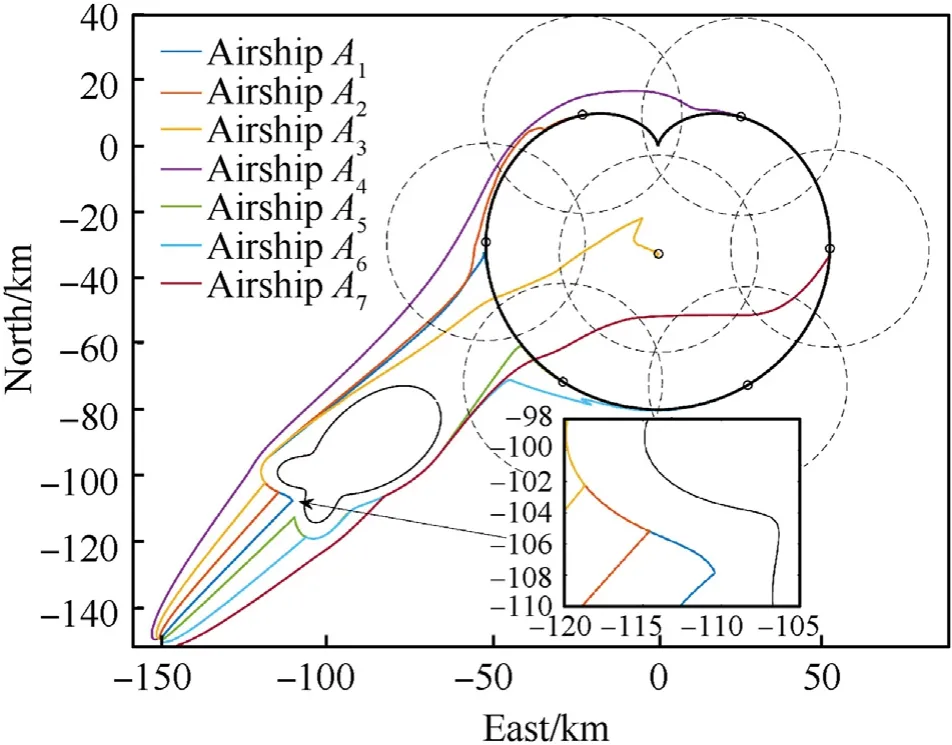
Fig.17. Trajectories of msas system and locations of target region and forbidden region with the proposed method without consideration of the dynamics and kinematics model.

To better investigate the effects of the proposed method,several supplementary simulation analyses are given in Fig.18-Fig.20.As shown in Fig.18,on the occasion of failure in one of the airships that are performing the task of covering the target region, the MSAs system and its performance can be successfully supplemented by the effect of the proposed method. On another occasion that the number of released airships is short to fully cover the entire target region,Fig.19 shows that the proposed method can make sure part of the target region could be fully covered by existing airships,which means the service performance of this MSAs system can be maximized. Considering the application scenario that airships in the formation are exposed to different wind fields, the simulation result is given in Fig. 20 in which external disturbances are set differently as di=[400 ＋200di,r（N）,50 ＋100di,r（N）,1000 ＋1000di,r（N•m）］Τwithdi,r= 0˙1isin（t／120）＋0˙15icos（t／360）. In the consideration that every airship in the formation is exposed to the different wind field, the external disturbances are different for different airships. Thanks to the adaptive design in the tracking controller,the difference of external disturbances theoretically has little influence on the formation coverage performance. The simulation result in Fig. 20 also proves it.

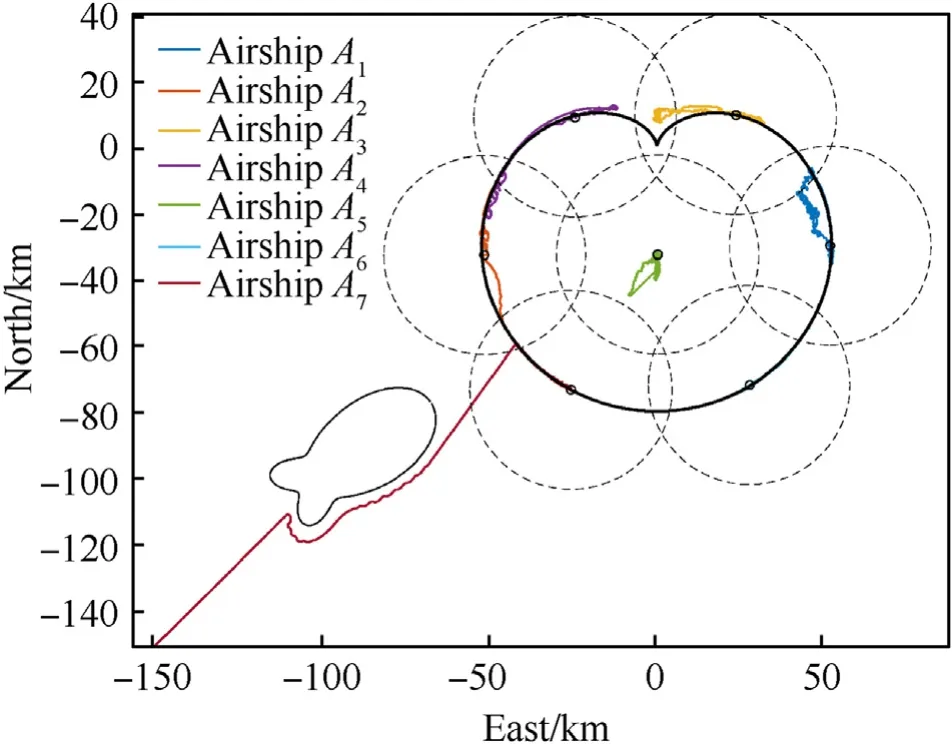
Fig.18. Trajectories of MSAs system with supplementation on the occasion of failure in one of initial stratospheric airships.

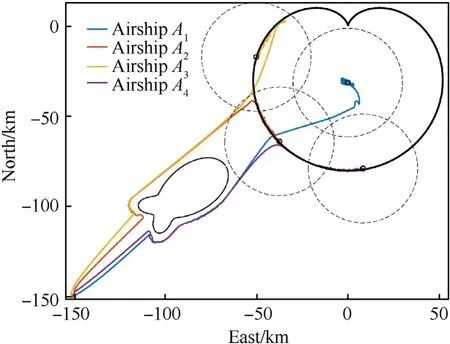
Fig.19. Trajectories of MSAs system when the number of stratospheric airships is short to fully cover the target region.

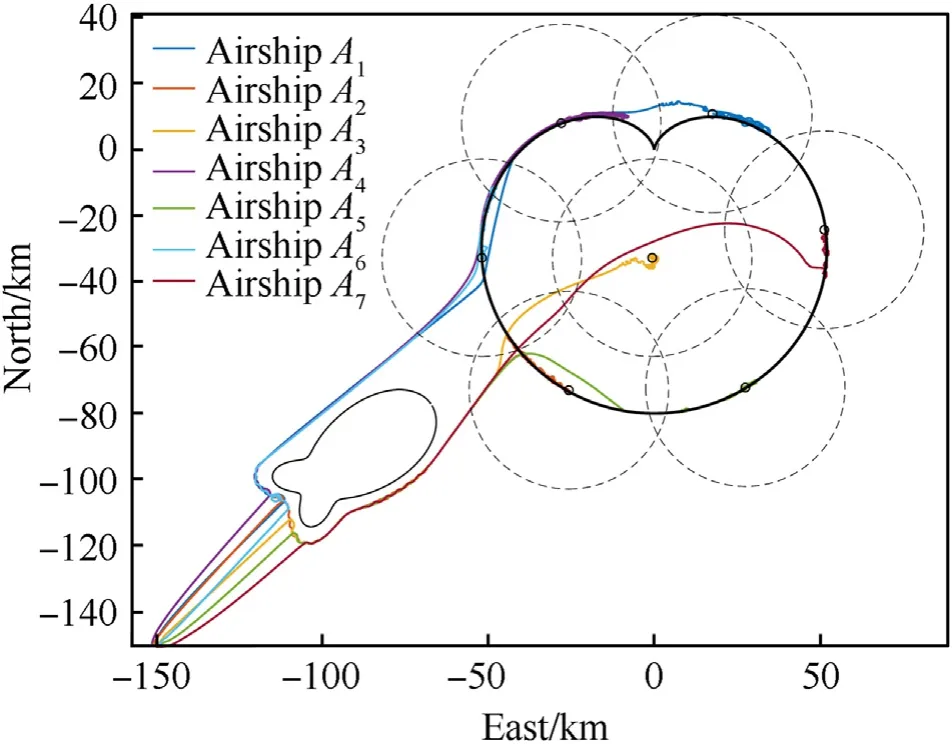
Fig. 20. Trajectories of MSAs system when MSAs members are exposed to different wind fields.

5. Conclusions

In this paper, we propose a control framework for the region coverage control problem using the MSAs system considering several practical application problems such as unknown individual differences, external disturbances, avoidance of forbidden region,and shortness of released airships. Under the effectiveness of the proposed virtual control law with a novel APF-based self-triggered mechanism, the local minimum problem of APF is solved. At the same time, communication and computation resources are saved significantly as continuous state information transmission and control inputs computation is avoided by the effect of the designed combined self-/event-triggered mechanism. Towards the aforementioned method, the Lyapunov stability and exclusion of Zeno behavior are proved mathematically. Simulation results illustrate the effectiveness of the proposed method. Moreover, several supplementary simulation analyses are given to better investigate the effectiveness of the proposed method.In future studies,we aim to conduct a high-altitude flight test to evaluate the performance of the proposed controller in reality. Moreover, region coverage control of MSAs system with the consideration of energy constraints and communication delay will be investigated in our future work.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the Postdoctoral Science Foundation of China(Grant No.2020TQ0028),the National Natural Science Foundation of China (No.62173016) and Beijing Natural Science Foundation, PRChina (No.4202038).