Vibration characteristics of sandwich plates with an auxetic honeycomb core and laminated three-phase skin layers under blast load

Quoc-Ho Phm , Vn Ke Trn , Trung Thnh Trn ,*

a Faculty of Engineeringand Technology,Nguyen Tat ThanhUniversity,Ho ChiMinhCity, Viet Nam

b Facult y of MechanicalEngineering,Le QuyDon TechnicalUniversity,Hanoi,VietNam

Keywords:Laminated three-phase Sandwich plate Auxetic honeycomb ES-MITC3 element High-order shear deformation theory

ABSTRACT

1. Introduction

1.1. State-of-the-art review

Before the requirement to protect weapons, equipment and fortifications against the attack of weapons, military equipment,and especially the impact of explosive loads. Nowadays, with the development of materials science, scientists have invented honeycomb structures with negative Poisson’s ratio (namely auxetic materials) inspired by nature as shown in Fig.1. Unlike sandwich plates with a folded core [1—6], sandwich plates with an auxetic honeycomb core offer more positive benefits than traditional positive Poisson's ratio materials such as impact absorption,increasing bending stiffness and shear resistance, fracture resistance [7], etc.Studying the mechanical behaviour of honeycomb structures can summarize several case studies such as Wan et al.[8]analyzed the impact of negative Poisson's ratio while Zhang et al. [9] examined the dynamic crushing problem. Zhu et al. [10] computed the nonlinear vibration of honeycomb sandwich plates by employing the third-order Galerkin approach.Duc et al.[11,12]introduced the exact solution to compute the nonlinear dynamic behaviour of sandwich plates/shells. In addition, Cong and co-workers [13]developed a new third-order exact approach to examine the dynamic problem of auxetic sandwich shells. Recently, Tran et al.[14—16] novel the finite element procedure to analyze forced vibration of auxetic honeycomb sandwich plates. Nguyen et al. [17]employed polygonal-isogeometric analysis(IGA)to investigate the mechanical behaviour of auxetic honeycomb sandwich plates.

Fig.1. The honeycomb nest in nature (source: internet).

Sandwich structures are basically fabricated by attaching two thin skins to a thick lightweight core.Recently,sandwich structures have been used popularly in aerospace vehicles due to their outstanding bending rigidity, low mass density, good noise cancellation and insulation.However,they are highly susceptible to failure due to stress concentration at load areas, the geometrical and material discontinuities. Investigating the mechanical behaviour of sandwich plates can include some typical works such as Kallannavar and co-workers analyzed the influence of temperature and moisture on the free vibration behaviour of skew sandwich plates with CNTRC core[18]and skew laminated hybrid composite and sandwich plates [19] by using finite element procedure. In addition, he employed the negative velocity feedback control-law to control a few of the first mode shapes of this sandwich plate[20] and studied the effect of temperature and moisture on the vibration response of skew laminated composite sandwich plates based on a neural network-based prediction model [21]. Besides,Youzera et al.[22]examined the damping and forced vibrations of three-layered beams using the higher-order zig-zag theory.Zaitoun et al. [23] employed an analytical method to study the buckling temperature of FG sandwich plates located on a viscoelastic substrate. Kouider et al. [24] investigated the static and free vibration response of sandwich plates with different types based on fourvariable quasi-3D shear deformation theory. Abualnour et al. [25]introduced a new four-variable trigonometric refined plate theory to consider the thermomechanical of reinforced composite plates.Sahla et al. [26] analyzed the free vibration sandwich plates using an analytical solution.Belbachir et al.[27]based on a refined plate theory to study the nonlinear thermal bending of sandwich plates.Moreover, readers can find valuable results on mechanical behaviour analysis of sandwich structures in literature [28—36].

In recent years,CNTs and GNPs have been extremely utilized as reinforcements in composite structures in different engineering fields including civil, mechanical, and aerospace engineering[37—40]. The investigations have been done to study the mechanical behaviour of three-phase polymer/GNP/fiber and/or polymer/CNT/fiber structures. Specifically, Saeedi et al. [41] used the Eshelby-Mori-Tanaka approach to analyze the influence of agglomeration of CNTs on the vibration of polymer three-phase polymer/CNT/fiber beams. Also using this approach, Swain et al.[42] proposed an eight-node element to calculate the vibration of three-phase polymer/CNT/fiber shells. Rafiee and co-workers [43]analyze the nonlinear influences on the thermal post-buckling,bending, and free vibration analyses of three-phase polymer/GNP/fiber beams using the Euler—Bernoulli beam theory with von K′arm′an geometric nonlinearity.Moreover,Cheng et al.[44]gave a model for evaluating the mechanical properties of three-phase polymer/CNT/fiber structures. Noroozi and his colleagues [45]examined the response of three-phase polymer/CNT/fiber doublycurved shells subjected to impact loading by using FEM based on Reddy's HSDT. Yousefi et al. [46,47] calculated the vibration problem of three-phase polymer/CNT/fiber conical shells and panels incorporating the CNTs agglomeration. Karamiasl et al. [48]examined the nonlinear vibration analysis of multilayer cylindrical nanoshells made of three-phase polymer/CNT/fiber in some layers and the three-phase polymer/GNP/fiber in other layers. Moreover,Jeawon et al. [49] focused on optimizing the frequency of plates made of three-phase polymer/GNP/fiber structure using a Sequential Quadratic Programming algorithm.

Research on the mechanical behaviour of structures subjected to blast loads can include some typical works such as the dynamic problem of the honeycomb structures[50—54].Recently,Duc et al.[55] analyzed the nonlinear vibration of FGM plates. Qi and coauthors [56] studied the forced vibration of curved sandwich panels. Tan et al. [57] studied blast-wave impact mitigation. Besides, Schenk and co-workers [58] computed the folded cores sandwich beams. In general, the above works all use analytical solutions.

To boost the computational efficiency of a traditional triangular element, the ES-MITC3 element [59—65] is produced by the association of the MITC3 element [66] and S-FEM [67—72]. Using this element has the following advantages: (1) It is easy to mesh the element even for complicated domains and is less affected by irregular meshing [59,60]; (2) Overcome the shear-locking phenomenon even with very thin structures [59,60]; (3) Employing this element is more accurate than using the MITC3 element [66],the DSG3 element [73], the CS-DSG3 element [74], and has the same performance as employing the MITC4 element[75].

1.2. Novelty of the article

From the comments of the above-mentioned studies, the main goal of this work is to develop the higher-order ES-MITC3 element for the vibration characteristics of sandwich plates with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skins.The HSDT is used to further improve the accuracy of the ESMITC3 element [60,65]. Some examples are conducted to confirm the performance of the current method.Finally,the impact of input parameters on the vibration characteristics of sandwich plates with an auxetic honeycomb core and laminated three-phase skins are fully provided.

2. Material properties of sandwich plates

2.1. Material properties of the auxetic honeycomb core

In this work, an auxetic honeycomb core with geometric parameters as plotted in Fig. 2, in which

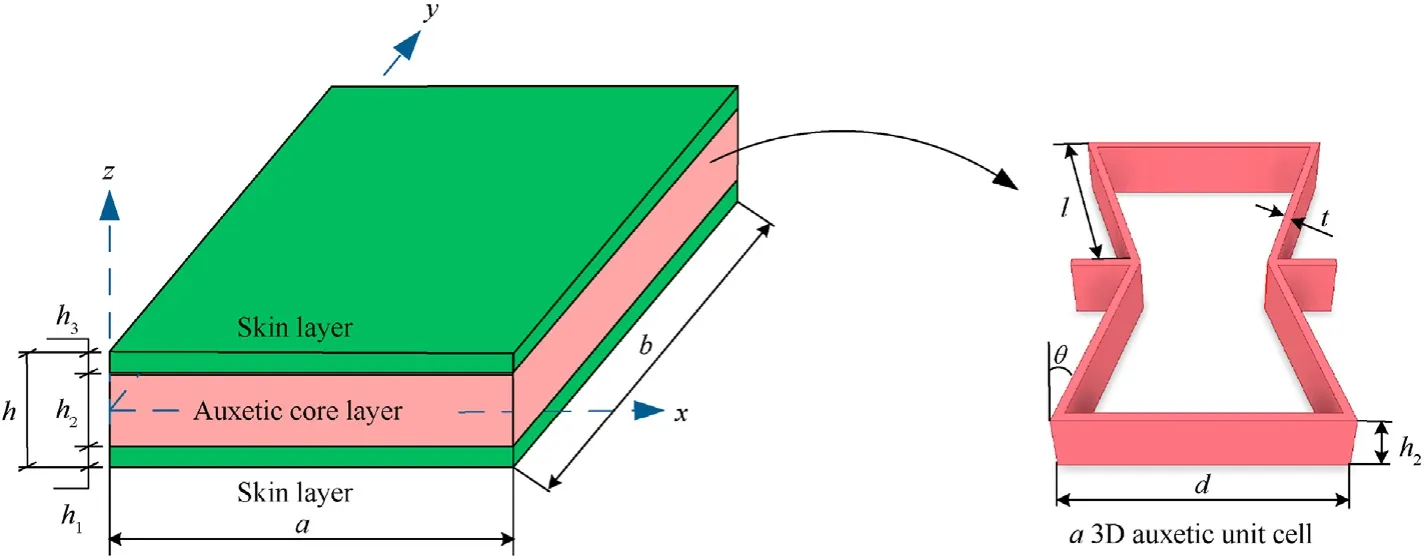
Fig. 2. Scheme of the sandwich plate with auxetic honeycomb core and two laminated three-phase skin layers.

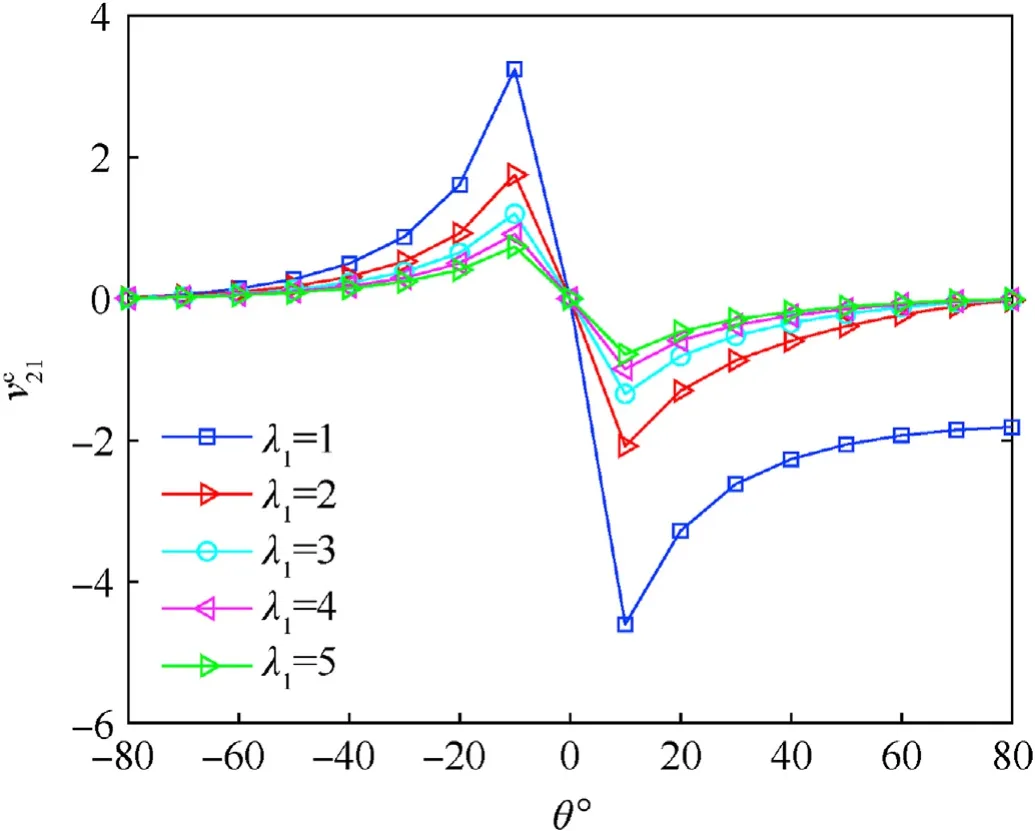
Fig. 3. The Poisson's ratio versus values of θ and λ1.

lis the length of the inclined rib;

dis the length of the vertical cell rib;

tis the thickness of the rib, and α is the inclined angle.

The mechanical properties of the honeycomb core are defined by Refs. [10,17].

where λ1=d／land λ3=t／l. The influence of inclined angle θ on Poisson'sratio when λ1=1,2,3,4,5 and λ3=0˙1 is plotted in Fig.3.We can see that θ gets values from 0◦to 80◦Poisson’s ratio gets a negative value.In addition,Poisson's ratio of υc21via the values of θ and λ1is listed in Table 1.

Table 1Poisson's ratio υc21 of an auxetic honeycomb core values of θ and λ1.

2.2. Three-phase skin layers

In this article, the three-phase skin layer is polymer/GNP/fiber.To fabricate these skin layers, we take the following steps: first,uniformly distribute GNPs in the polymer matrix;then,it is further reinforced with fibers. The effective mechanical properties of structures can be achieved in the following two subsections.

2.2.1. Material properties of GNP-reinforced polymer

Following the rule of mixture, the Poisson’s ratio υGmand the density ρGmof the GNP reinforced polymer are obtained in terms of volume fractions (Vm＋VGNP= 1) as follows:

To calculate GNPs volume fraction, the following relation in terms of weight fraction (WGNP) is expressed [76]:According to the Halpin-Tsai model, the GNP-reinforced polymer's effective elastic modulus is presented by Ref. [77].

in which

withWGNP,lGNP, andhGNPsequentially are the width, length, and thickness of the GNPs.

2.2.2. Material properties of three-phase skin layers

A three-phase polymer/GNP/fiber density is defined according to the rule of the mixture as follows (VGm＋VF= 1):where the fibers volume fraction is computed in terms of the weight fraction (WF) as Ref. [76]

For the three-phase skin layers, the elastic modulishear moduliand Poisson’s ratioare gained utilizing the following equations:

Note that, symbolsm, GNP,Gm,F, andfdenote the polymeric matrix, GNPs, GNP-reinforced matrix, fibers, and skin layers,respectively.

3. Blast load

According to the study by Lam et al.[78],the blast loadp（t）is a short-term load generated by an explosion, supersonic projectile and/or rocket operating in its vicinity.It is defined as the following formula (see Fig. 4):

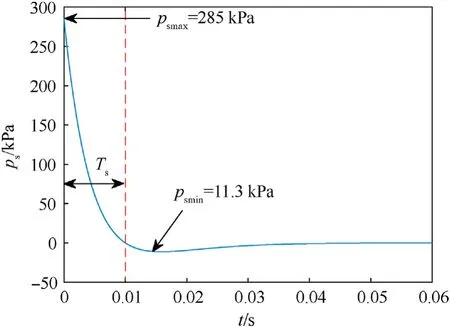
Fig. 4. Blast pressure function.

in which

1˙8 is the effect factor of a hemispherical blast;Psmaxis the maximum static over-pressure;

bis the parameter controlling the rate of wave amplitude decay;Tsis the parameter characterizing the duration of the blast pulse.

4. Mathematical formulation

4.1. C0 higher-order shear deformation theory

The displacement field of the sandwich plate based on the C0-HSDT is defined by Ref. [79].

in whichu0,v0,w0,φx,φy,ψxand ψyare displacement variables,and

The strain-displacement relations are defined by

where

The membrane strain is

The bending strain is

The transverse shear strain is

with

The stress-strain relation of sandwich plates obeying to Hooke's

law is

herein

For the auxetic honeycomb core [16].

For the three-phase skin layers [79].

wherem=cos（φk）andn=sin（φk）in which φkstands for the fiber angle in thekth layer, and

4.2. Weak form equations

Using Hamilton's principle, the motion equation of the sandwich plate is given by Ref. [79].

where U , K , and Π are respectively the strain energy, the kinetic energy, and work done by external loads. herein

The strain energy is

in which

and

with A, B, D, E, F, H, As, Bs, Dsare calculated by

The kinetic energy is

where

and m is the inertia matrix

with

The work done by applied force is

Substituting Eq. (21), Eq. (26), and Eq. (30) into Eq. (20), the weak formulation for the dynamic analysis of the sandwich plate is

5. Finite element formulation

5.1. The MITC3 element

According to the formulation of the higher-order MITC3 element, the membrane and bending strains are determined by Refs. [62,66].

where

The transverse shear strains of the MITC3 element are interpolated from typing points (the centre of triangular element edges)[66] and are defined as follows:

where

in whicha=x2-x1;b=y2-y1;c=y3-y1;d=x3-x1(see Fig. 5(a)),Aedenotes the area of the triangle element, and de=is the displacement vector of the element node (j=1-3).

Fig. 5. (a) The local coordinate of the triangular element; (b) The formation of smoothing domains Ωk.

Substituting the discrete displacement field into Eq. (31), the motion equation of sandwich plates is obtained by

in which

The stiffness matrix plate K is

where

The mass matrix plate M is

The loading vector plate F is:

with

withpis the magnitude of the uniformly distributed load which is perpendicular to the neutral plane of the sandwich plate,and N is a shape function matrix [16].

5.2. The ES-MITC3 element

Using the ES-FEM for MITC3 element, the smoothed strain ~εkand the smoothed shear strain ~γkover the smoothing domain Ωkare computed by integrating the compatible strain ε and the shear strain γ in Eq. (28) as follows [67]:

where φk（x） is the smoothing function satisfying the condition= 1. In this work, we use the smoothing function as follows [67]:

withAkis the area of the smoothing domain Ωkdefined by

in which Ωkis an edge-based smoothing domain connected with the inner edgekas presented in Fig. 5(b);nekis the total of the adjacent triangular elements;Aiis the area of theithtriangular element associated with the edgek˙

Substituting Eq.(32)—Eq.(34)and Eq.(44)into Eq.(59)and Eq.(60),the smoothed strains on the domain Ωkare given by Ref.[67]

Then, the global stiffness matrix is determined by

in which

5.3. Solution process

From the differential equation of the plate element Eq.(31),we obtain the motion equation of the entire sandwich plate as follows:

where K,M and F are respectively the global stiffness matrix, the global mass matrix and the global load vector are defined by

when F = 0, the equation for the determination of natural frequencies is

in which ω is the natural frequency.

If the force vector is a function of time F =F（t）and includes the structural damping, the vibration equation of the plate Eq. (69) is re-written by

in which C is the global structural damping matrix which is defined by Refs. [80—83].

with α and β are Rayleigh drag factors computed through damping ratio ζ and the first two natural frequencies [80]

To solve this equation, the authors employ the Newmark-beta approach with integration steps that can be found in documents[80—83] and flowchart as demonstrated in Fig. 6.

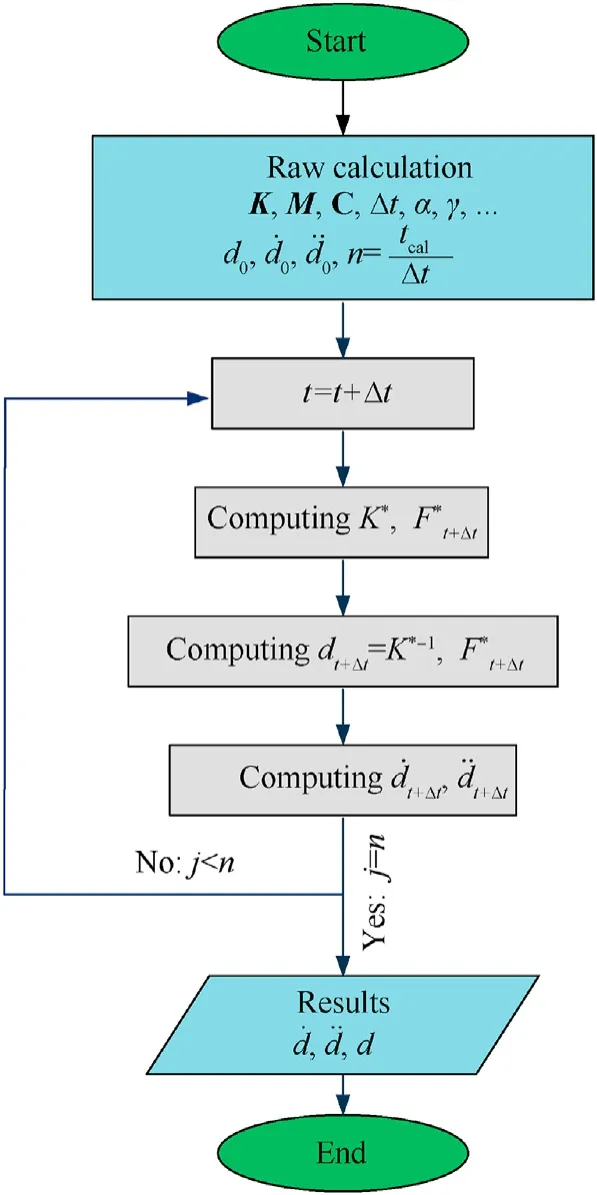
Fig. 6. Scheme of Newmark-beta method.

Note that, for the finite element analysis, boundary conditions(BCs)are taken according to the geometric constraints at the edges.In this paper, BCs are given and denoted as follows:

-Clamped (C):

-Simply supported (S):

- Free support(F):all degrees of freedom(DOFs)at the boundary edge do not equal zero.

6. Results and discussions

Based on the established finite element formulas above, the authors proceed to write code by Matlab software. Then, some examples are performed to illustrate novel contributions including:(1)Verifying the reliability of the proposed method;(2)Presenting new results in the free and forced vibration of sandwich plates.

6.1. Verification study

Example 1.Considering a fully simply supported(SSSS)sandwich square plate (a=b;h=a／10) with a pure ceramic core and two FGM skin layers. The bottom-core-top thickness ratio of the sandwich plate ish1-h2-h3= 2-1-2 with materials properties as shown in Table 2. The dimensionless natural frequency is given by the equation:

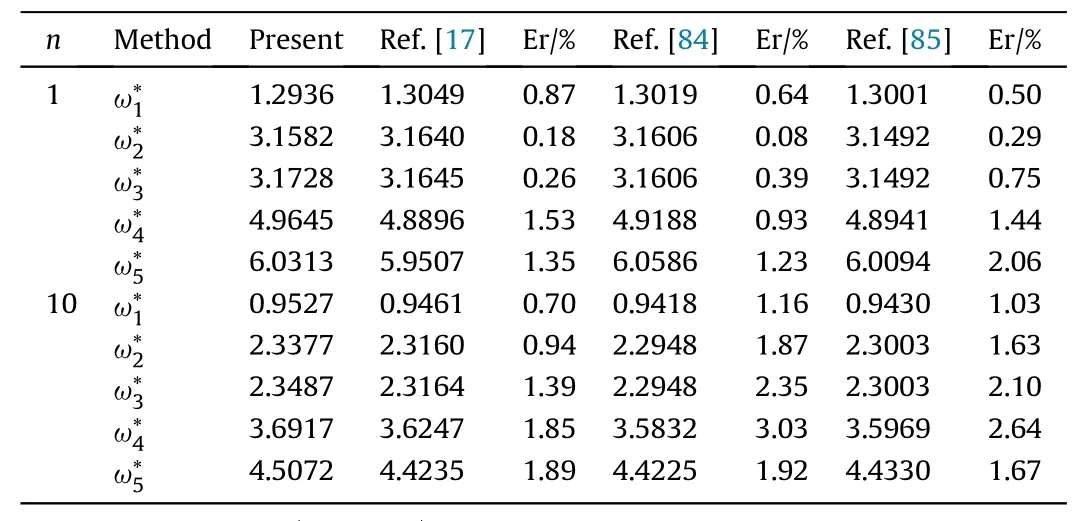
Table 2Comparison of dimensionless frequencies of SSSS sandwich plates.

The convergence study of the ES-MITC3 element was concluded in studies [61,64], so the authors use 18×18×2 element meshes for the next works. The first five dimensionless frequencies of sandwich plates in comparison with those of IGA-based polygon elements [17], QUAD-8 using HSDT (Q8-HSDT) [84], and IGA-TSDT[85] are presented in Table 2. It can be confirmed that the gained results of the current method match well with those of other published (maximum error of approximately 3%).

Example 2.Let’s consider a fully clamped (CCCC) homogeneous square plate with parametersa=b=1 m,h=a／10,E= 30 GPa,ρ=2800 kg／m3and υ =0˙3.The plate is subjected to a distribution sudden loadp0=10 kPa.The dimensionless deflection is given by the formula:

The deflection response of the plate centre is plotted in Fig. 7.From this figure,it can be observed that the deflection response of the plate centre is compared to Ref. [86] which uses Meshless Petrov-Galerkin method is approximately the same in both shape and value. From these two examples, it can be affirmed that the author's formula and program guarantee accuracy and reliability.

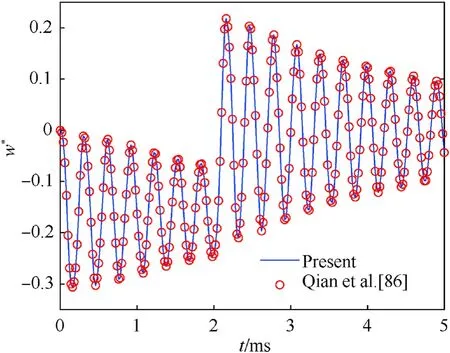
Fig. 7. The displacement response of the plate centre over time.

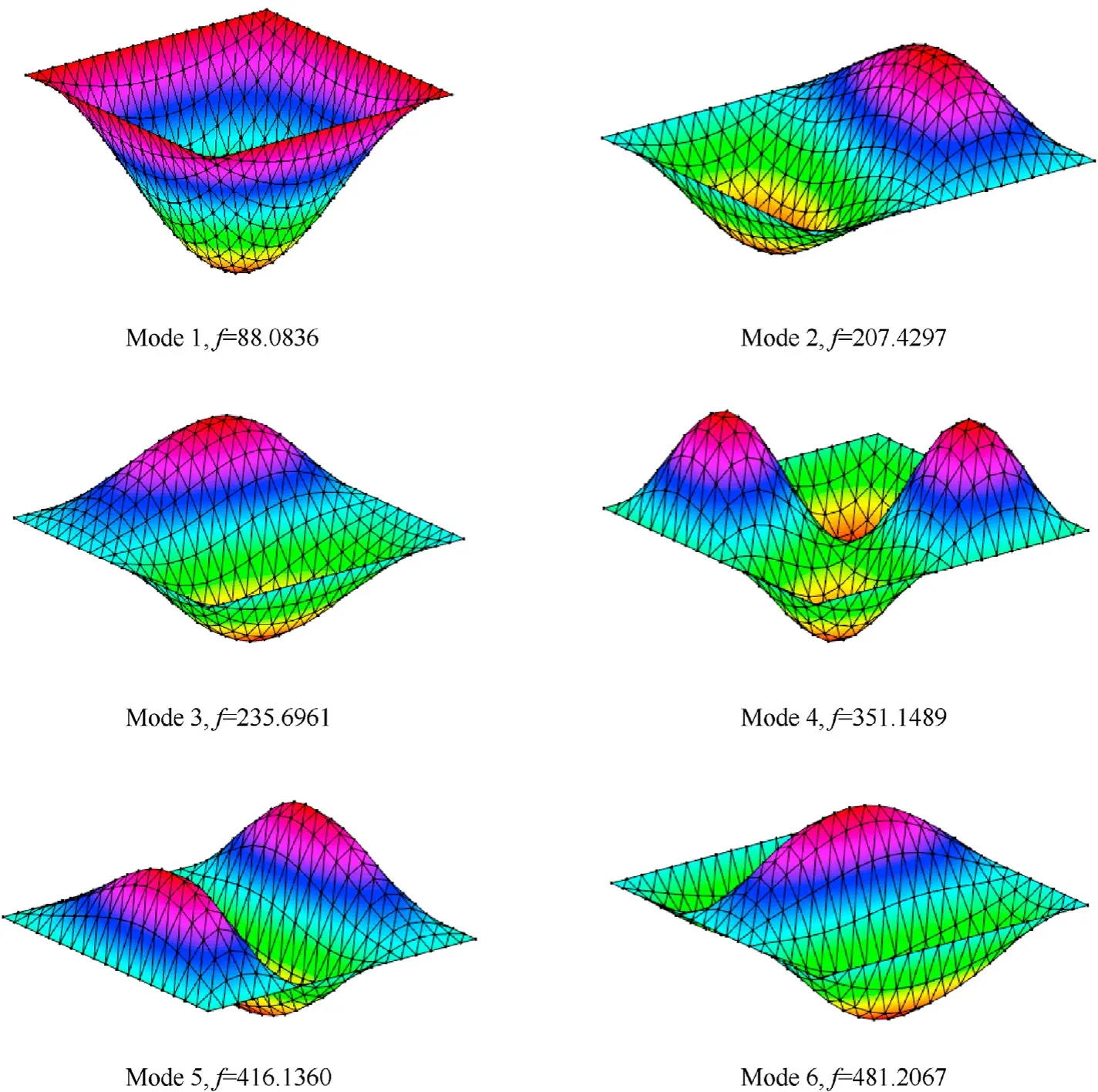
Fig. 8. Mode shapes of the sandwich plate in the first six vibrational modes.

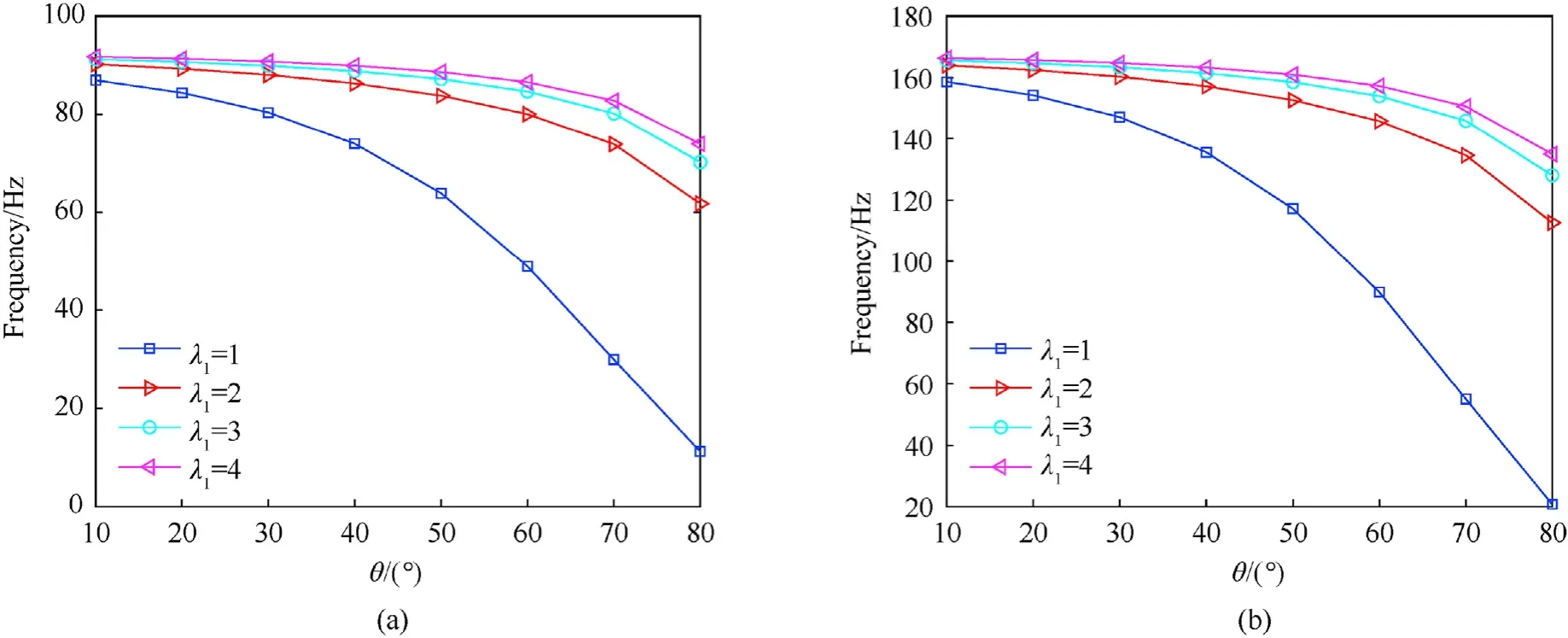
Fig. 9. Effects of geometrical parameters a and λ1 on natural frequencies: (a) The SSSS sandwich plate; (b) The CCCC sandwich plate.

6.2. Free vibration analysis

In this section, the sandwich plate with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers is studied. The geometrical parameters asa／b= 1,a／h=50 (ais fixed),h1=h3, andh2／h1= 2. The auxetic honeycomb core is made of aluminium (E0= 70 GPa,ρ0= 2702 kg／m3) with λ1= 2,λ3=0˙1,and θ =30◦.The thickness of the skin layers is identical,and they are made of epoxy,GNPs,and glass fibers.The mechanical properties of epoxy (matrix) areEm= 3 GPa, υm= 0˙34, and ρm=1200 kg／m3and mechanical properties of the GNPs are areEGNP=1˙01 TPa,υGNP=0˙186,ρGNP=1060 kg／m3,dimensions of the GNPs are stated aslGNP= 2˙5 μm,wGNP= 1˙5 μm,hGNP=1˙5 nm, and weight fraction of the GNPs is presented asWGNP=0˙01 [49]. Each face sheet consists of four layers of φ=[90／450／450／900］and the glass fibers’mechanical properties areEF11=EF22=73˙084 GPa,GF12=30˙13 GPa,υF12=0˙22,and ρF=2491˙191 kg／m3withWF=0˙85 [87]. To see the strain field smoothing effect when using the ES-MITC3 element,Fig.8 displays the first six mode shapes of the SSSS sandwich plate.

In addition, Table 3 lists the first natural frequencies of the sandwich plate with the same input parameters as the above example versus values of θ and λ1with λ3=0˙1.Furthermore,the effects of these two parameters on the vibration of the sandwich plate are also illustrated in Fig.9.It can be observed that the natural frequency decreases slightly when the inclined angle θ of cells increases from 10◦to 30◦with each value of λ1. However, the frequency tends to decrease faster as θ gets values greater than 40◦.Besides, for all values of θ when increasing λ1makes increases the frequencies of sandwich plates. From obtained results, we can see that values of θ and λ1affect significantly the free vibration of sandwich plates,especially when λ1=1.Moreover,sandwich plates with the CCCC boundary are the stiffest of all BCs so they have maximum natural frequencies.

Table 3Natural frequencies (Hz) of sandwich plates via values of θ and λ1.

Next,the first natural frequencies of square sandwich plates with input parametersa／h=20,h2／h1=4 versus values of λ1and λ3are shown in Fig.10. Observing this figure,we can see that natural frequencies decrease rapidly as λ3increases from 0.1 to 0.5 for λ1gets values less than 2, while it decreases more slowly for λ1> 2. The numerical results also show that the increase of λ1lead to increasing gradually of natural frequencies with each value of λ3. It can be found that the increase in the thickness-to-length ratio λ3in the auxetic unit cell makes increase the inertia and stiffness of the sandwich plate. Thus, to achieve higher natural frequencies, it is recommended to use honeycomb cores with thinner walls,however,this makes the auxetic honeycomb cores fragile and vulnerable.

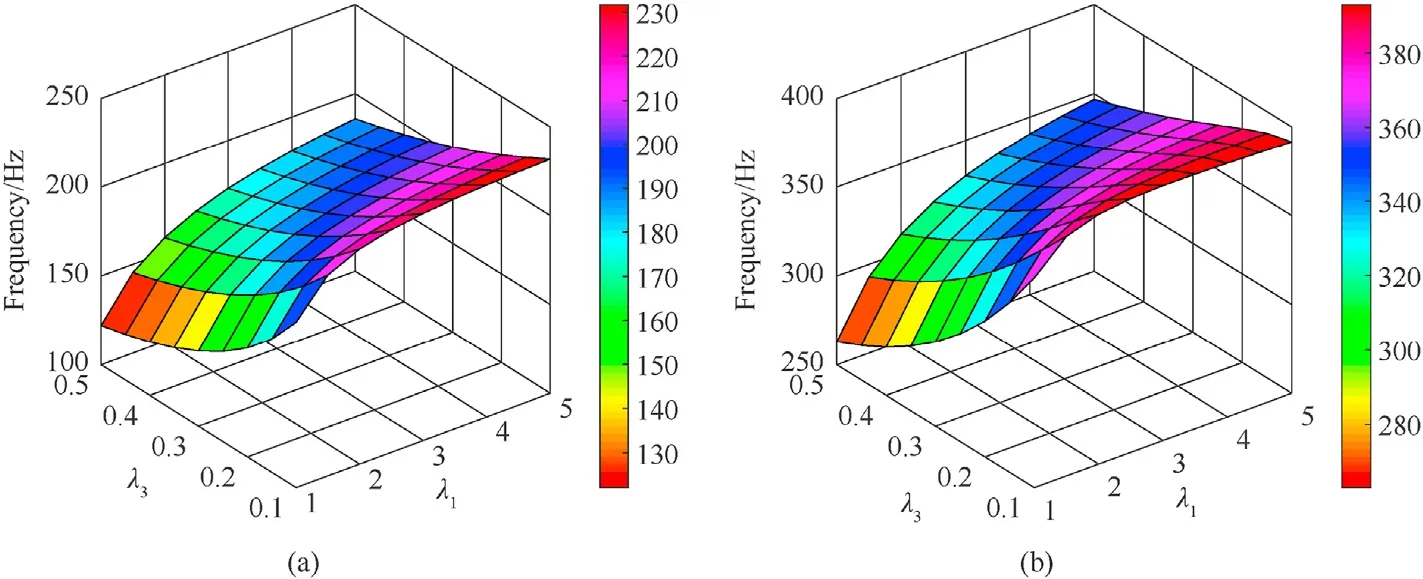
Fig.10. Effects of geometric parameters λ1 and λ3 on natural frequencies of sandwich plates:(a)The SSSS sandwich plate with θ =30◦;(b)The CCCC sandwich plate with θ = 20◦.

Moreover, the simultaneous effect of the length-to-thickness ratioa／hand the thickness ratio between layersh2／h1on the free vibration of square sandwich plates witha=10◦and λ3=0˙1 is reported in Table 4.It can be seen that the influences of geometric parameters(especially the geometric parameters of an auxetic unit cell) on the natural frequencies of sandwich plates are very complex. Hence, it is not easy to explore the general rule for the frequencies of sandwich plates with auxetic honeycomb and laminated three-phase polymer/GNP/fiber skin layers. In general,thicker plates will be stiffer resulting in higher frequencies as expected and reasonable honeycomb core thickness leads to maximum natural frequency while mass is reduced. Furthermore,Table 5 gives the first six natural frequencies of sandwich plates with input parameters:a／h= 60;h2／h1= 8; λ1= 3˙5, and λ3=0˙1.

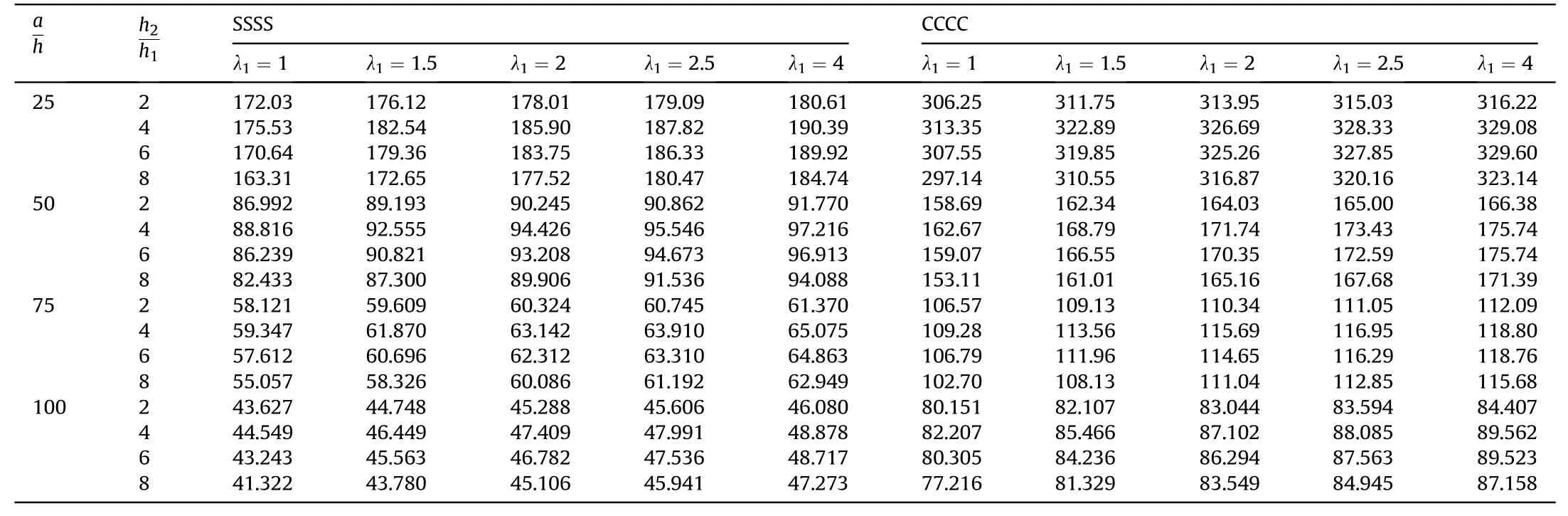
Table 4Impacts of ratios a／h and h2／h1 on the free vibration of sandwich plates.

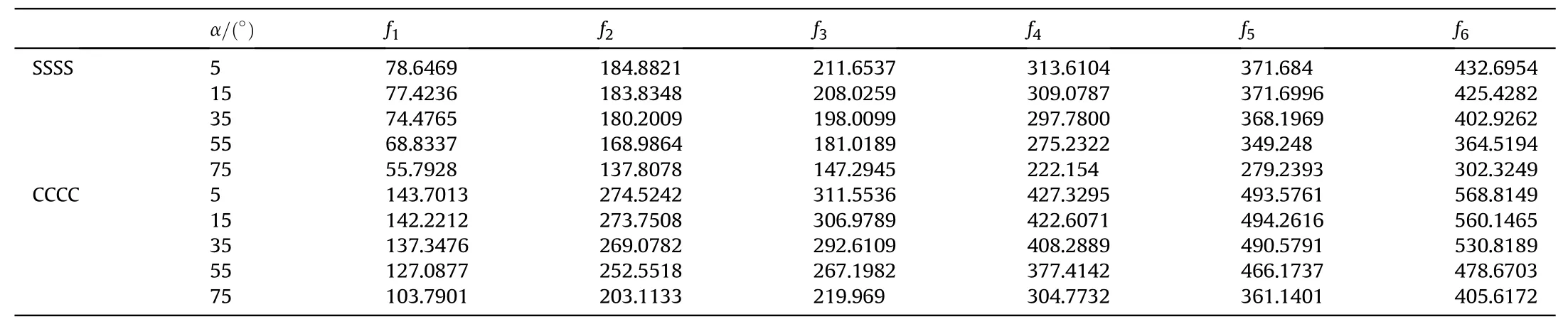
Table 5The natural frequencies of sandwich plates.

6.3. Dynamic response analysis

Firstly, the simultaneous effect of ratioh2／h1(h1=h3) on the dynamic response of SSSS square sandwich plates with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers under blast load is presented in Fig.11.From this figure,it can be observed that an increase in the thickness (h2) of an auxetic honeycomb core leads to an increase in deflection/velocity/acceleration response of the sandwich plate centre.This also led to the conclusion that the thicker laminated three-phase polymer/GNP/fiber skin layers contributed to the increased stiffness of the sandwich plate and well protected the inner auxetic honeycomb core.

Fig.11. Effect of ratio h2／h1 on the dynamic response of SSSS square with sandwich plates an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers under blast load:(a)Deflection response of the sandwich plate centre;(b)Velocity response of the sandwich plate centre;(c)Acceleration response of the sandwich plate centre;d)The phase trajectory.

Next, Fig.12 shows the influence of auxetic unit cell parameterλ1on the dynamic response of SSSS square sandwich plates with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers subjected to blast load.We can conclude that λ1has no sensitive influence on the vibration of the sandwich plate. This figure also illustrates that by increasing λ1from 1 to 3, a slight reduction in the deflection of the plate centre can be observed.

Fig.12. Effect of the parameter λ1 on the dynamic response of SSSS square sandwich plates with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers under blast load: (a) Deflection response of the sandwich plate centre; (b) Velocity response of the sandwich plate centre; (c) Acceleration response of the sandwich plate centre; (d) The phase trajectory.

Finally,Fig.13 plots the impact of unit cell auxetic parameter λ3of CCCC square sandwich plates with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers subjected to blast load.It can be seen that the effect of parameter λ3on the dynamic response of sandwich plates is more obvious than the parameter λ1.In other words,the parameter λ3is more sensitive than the parameter λ1for vibration characteristics of sandwich plates.An increase in the thickness of the auxetic unit cell increases the stiffness of sandwich plates resulting in reduced deflection,but it also increases the mass of sandwich plates. Selecting these parameters appropriately can reduce the vibration of sandwich plates.

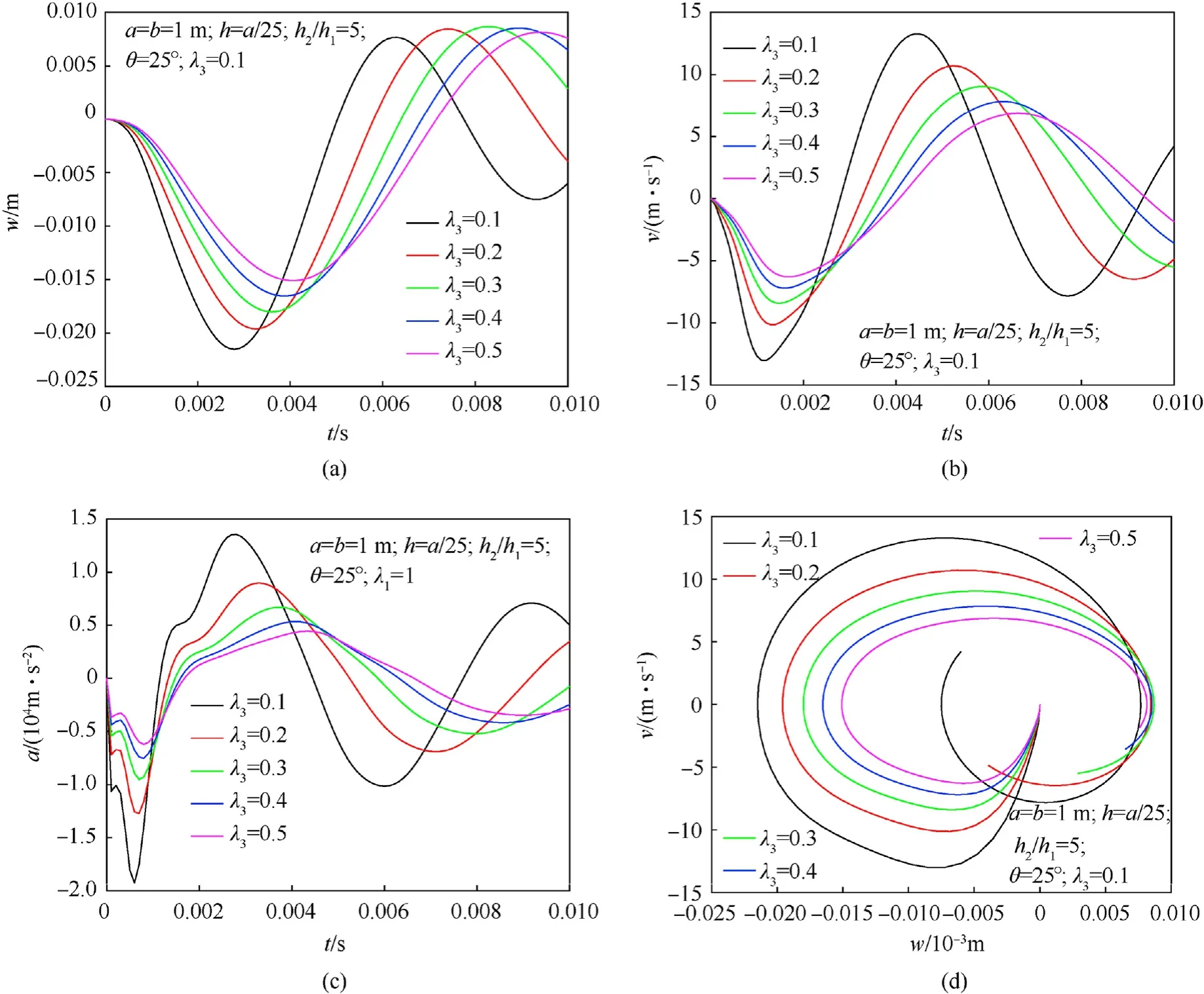
Fig.13. Effect of parameter λ3 on the dynamic response of CCCC square sandwich plates with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers under blast load:a)Deflection response of the sandwich plate centre;(b)Velocity response of the sandwich plate centre;(c)Acceleration response of the sandwich plate centre;(d)The phase trajectory.

As is known, the phase plane is a coordinate plane, the horizontal axis represents displacement, and the vertical axis represents the velocity of the moving object to be investigated. Each state of motion of an object gives only one displacement-velocity value pair, corresponding to only one point on the phase plane.This point is called the representative point of the state of motion.The graph depicting the motion trajectory of a representative point on the phase plane is called the phase trajectory.Thus it represents the displacement and oscillation velocity, the phase trajectory reflects the change of the solution of the system of differential equations with time. The phase trajectories in the above cases are also detailed in Fig.11(d), Fig.12(d) and Fig.13(d). From these figures,it can be seen that the non-closed curves due to non-periodic oscillations. From the phase trajectory we also see that the oscillations are relatively stable, nothing unusual.

Furthermore,it can also be observed that,in the above cases,the sandwich plate oscillates very strongly, which is shown by the graph of the velocity and acceleration of the sandwich plate centre along the z-axis over time. However, the deflection of sandwich plates is small. This proves that the auxetic honeycomb core has a very good vibration absorption capacity. Note that, the damping ratio ζ=0˙1 is applied for the above examples. In fact that the damping structure always exists due to the influence of elements inside structures.

7. Conclusions

In this work, the vibration characteristics of sandwich plates with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers under blast load are successfully studied by employing the higher-order ES-MITC3 element. The HSDT is used to further enhance the accuracy of the ES-MITC3 element. From the numerical results, some notable conclusions can be summarized as follows:

(1) Using The ES-MITC3 element is easy to mesh for complicated structures and helps reduce computational costs. The HSDT is employed to cancel shear corrected factors and provide more accurate solutions.

(2) The finite element procedure can be used as one of the standard solutions for sandwich plates with auxetic honeycomb core and laminated three-phase polymer/GNP/fiber skin layers.

(3) The gained results present the complex effect of the honeycomb unit cell on the vibrations characteristics of sandwich plates. Furthermore, laminated three-phase polymer/GNP/fiber skin layers help to increase the sandwich plate stiffness and well protect the inner core layer under external loads,especially blast loads.

(4) The algorithm and program can be extended to analyze the dynamic response of different sandwich structures with complex geometric models that are not easily solvable by analytical methods.

(5) The survey results in our work promise to be helpful for the calculation and design of sandwich plates in practice.Finally,the proposed higher-order ES-MITC3 element can be applied for nonlinear problems of sandwich plates in the next studies in the future.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.