基于事件触发的非线性多智能体系统一致性

唐 云,唐朝君,魏正元

重庆理工大学 理学院,重庆 400054

1 引 言

近年来,由于多智能体系统的协同控制在各方面都有应用,已逐渐引起许多学者的关注。协同控制在机器人协作、传感器网络、和军事领域等方面都有体现[1-3],多智能体系统协同控制的目的是分析和设计一种控制协议,使得智能体之间通过相互协作能够高效率和快速地完成单个智能体所不能完成的目标,这一问题通常被称之为一致性问题。关于一致性问题的研究已经取得了许多的成果如文献[4-9]。

关于多智能体系统的一致性控制策略,许多学者提出了不同的设计方法,早期一种连续控制策略的方法被提出[10],连续控制策略是建立在每个智能体的资源充足,可以连续的交换信息之上,但是在实际的应用中,智能体自身的资源是并不是无限的,而且连续控制策略会加大智能体的通信负担和控制器的更新频次,降低了智能体的工作时长,所以在控制过程中就造成了许多资源的浪费。为了减少在系统控制过程中资源浪费的问题,文献[11]提出了一种周期采样控制,在相同的时间间隔,所有的控制器统一更新,这种控制方法在一定程度上降低了资源损耗,但是依然存在资源浪费的现象。为了解决这一问题,文献[12]就提出了一种基于事件触发控制的控制策略,即当前采样的测量值是否满足预先设定的事件触发函数,若满足事件触发函数,则控制器才会更新其状态值,反之亦然。所以可以明显的观察出相较于传统的采样控制,事件触发的控制协议,能保证系统的稳定性,同时使得控制器不在连续更新状态,只在离散时刻处触发,有效地实现节约资源.当前关于事件触发控制协议在一致性问题的研究中都有体现如文献[13-17]。文献[13,14]讨论了无向拓扑下一阶多智能体系统的一致性问题,提出了事件触发控制策略,在这种控制策略下,资源浪费的问题被有效地解决,但系统是建立在无向拓扑上,没有考虑现实中智能体的信息传输是有方向的,因此对有向拓扑的讨论是有意义的。文献[15]讨论了领导跟随事件触发多智能体系统的一致性问题,在事件触发控制策略下保证了跟随者渐进收敛到领导者的状态。文献[16,17]中Dimarogonas和Johansson利用无向拓扑的特性,设计事件触发控制协议,解决了多智能体系统的一致性问题,控制器是否触发取决于是否满足触发条件(测量误差相对于状态函数范数的比值)但系统并没有考虑非线性,为设计更贴近于生活的系统,非线性系统的研究是有必要的。

基于以上原因的分析,在上述文献的基础上设计了更一般的系统,研究了无领导事件触发一致性,不同之处主要有两点:第一,在许多网络系统中,智能体的信息交流是既有方向又有权重,设计的智能体的通信拓扑图是加权有向图。第二,在现实生活中大多数物理系统都是非线性的[18],为了使系统更具有一般性,设计的系统是非线性的,同时上述的文献的控制协议与设计的控制协议也不一样,控制协议更具有一般性。

2 预备知识和问题描述

2.1 预备知识

用三元组G=(V,E,A)表示智能体之间通信拓扑图,其中V={v1,v2,…vn}表示顶点集,vi表示第i个智能体;E⊆V×V表示有向图G的边集;A=[aij]∈Rn×n表示有向图G的邻接矩阵。图G是强连通的,如果满足图中任意两个顶点之间都有一条有向路径。设Ni={vj∈V|(vj,vi)∈E}表示顶点i的邻居集。令加权有向图G的Laplacian矩阵为L=[lij]∈RN×N其元素lij满足以下定义:

若存在顶点序列vi1,vi2,…vim其中(vij,vij+1)∈V则称从顶点vi1到顶点vim有一条有向路径。如果有向图中存在一个根节点,具有到其他所有节点的有向路径,则称该图包含一棵有向生成树。

引理1[19]设图G是强连通的,则存在ξ=(ξ1,ξ2,…,ξN)T使得ξTL=0,其中ξi>0,i=1,2,…,N且

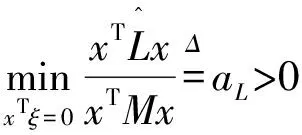
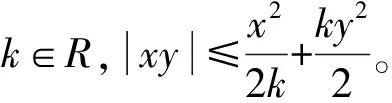
引理3[21]零是有向图G的Laplacian矩阵L的特征值,1=(1,1,…,1)T∈Rn是其对应的右特征向量,其他非零特征值均具有正实部,如果有向图G包含一个有向生成树,则0是L的简单特征值。

2.2 问题描述

考虑由N个智能体组成的多智能体系统,设第i个智能体的运动学方程可以表示为

(1)

其中,xi(t)∈R表示智能体i的状态,ui(t)∈R是智能体i的控制输入,f(xi(t),t):R×R→R表示智能体i的非线性连续函数。

假设1假定系统式(1)的非线性函数f(xi(t),t):R×R→R,存在l∈(0,+∞)满足:

|f(x,t)-f(y,t)|≤l|x-y|

(2)

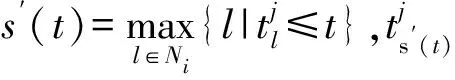
定义1 对于智能体的任何初始状态xi(0)(i=1,2,…,N),利用控制输入ui(t),使得所有智能体i满足:

则称系统式(1)实现一致性。

证明：显然FTLTLF是对称矩阵,则对于任意的向量δ,有δTFTLTLFδ≥0。

只需要证明:δTFTLTLFδ=0可以推出δ=0。

3 主要结果

3.1 集中式事件触发的一致性

首先研究如下的控制协议:

(3)

其中,ts表示智能体的第s次触发时刻。

定义第i个智能体的状态测量误差为

(4)

u(t)=-e(t)-αy(t)t∈[ts,ts+1)

(5)

由式(1)和式(5)可以得到:

(6)

其中:f(x(t),t)=(f(x1(t),t),…,f(xN(t),t))T

则:

(7)

定理1：对于多智能体系统式(1),假设有向图G是强连通的,控制增益满足:

(8)

限定触发条件满足:

(9)

ξmax=max{ξ1,ξ2,…,ξN},i=1,2,…N

在控制协议式(3)下,系统式(1)可以达到一致。

证明：对系统式(1)构造Lyapunov函数

(10)

对V(t)求导得:

(11)

由(7)式可以得:

‖y(t)‖‖M‖‖L‖‖e(t)‖+

yT(t)MLf(x(t),t)

(12)

令,H=yT(t)MLf(x(t),t)。

则:

H=yT(t)ML[f(x(t),t)-f(x1(t),t)1N]=

(13)

由假设1可知:

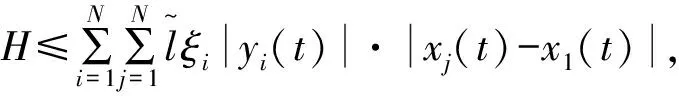
(14)

由式(12)和式(14),就可以得到:

‖y(t)‖‖M‖‖L‖‖e(t)‖+

(15)

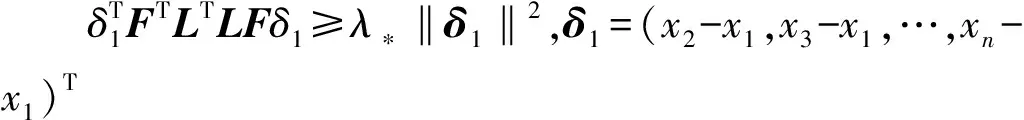
‖y(t)‖‖M‖‖L‖‖e(t)‖+

‖y(t)‖‖M‖‖L‖‖e(t)‖

(16)

根据式(9),得到

(17)

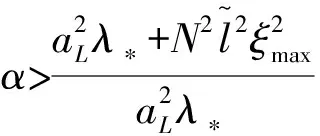
(18)

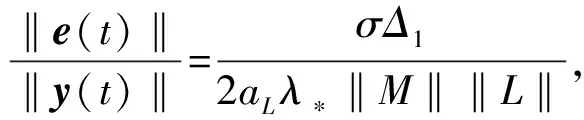
(19)

由假设1和定理1的证明过程可得:

(20)

因为

(21)

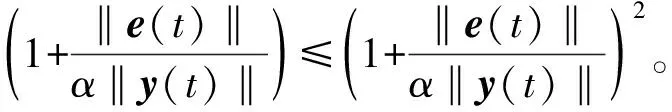
(22)

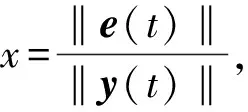
定理得证。

注:在控制协议式(3)中,假设系统中的智能体具有相同的触发时刻,触发时刻的计算需要用到全局信息,因此控制协议式(3)是集中式的控制协议。

3.2 分布式触发一致性

设第i个智能体的状态测量偏差为

(23)

(24)

证明：对系统式(1)构造Lyapunov函数:

(25)

对V(t)求导得:

(26)

由式(7)可以得:

|yT(t)MLe(t)|

(27)

令Q=yT(t)MLe(t),则可以得到:

(28)

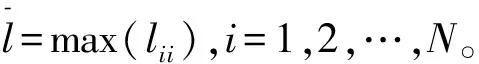
根据定理1,式(27)和式(28)可得:

(29)

(30)

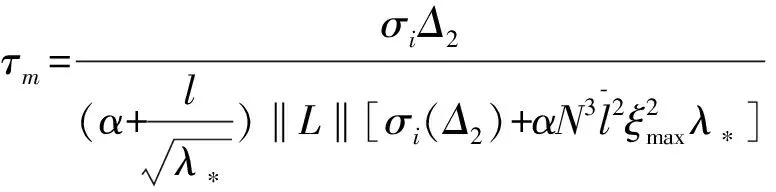
(31)

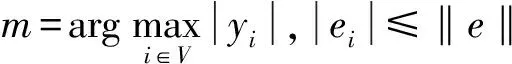
其余的证明和定理3类似,再结合式(24),可以解出:

定理得证。

4 仿真分析

考虑含有4个智能体的多智能体系统,系统通信拓扑对应的Laplacian矩阵如下:

设非线性函数f(xi(t))=sin(xi(t)),4个智能体的初始状态随机的选取为:x1(0)=-3,x2(0)=-2,x3(0)=1,x4(0)=2。

经过计算得到λ*=λmin(FTLTLF)=0.585 8,取l=1,M=diag{1,1,1,1},经过计算分析取α=30。

对于集中式的控制协议式(3),选取参数α=30,σ=0.5时,图1给出智能体的状态轨迹,图2给出了系统的状态误差随时间的变化,明显看出所有智能体只在特定的时刻才能触发。

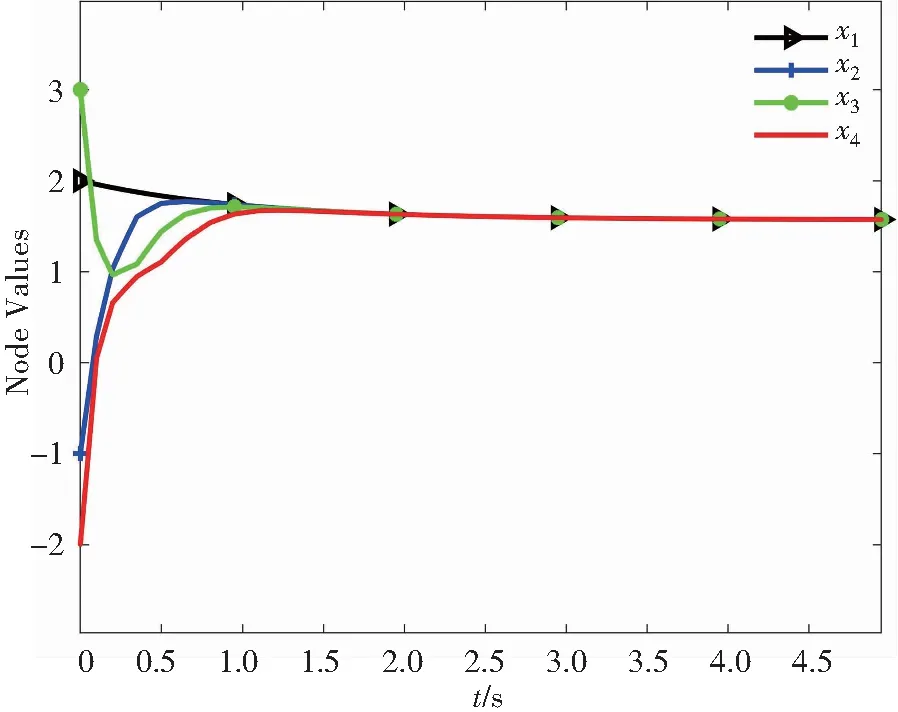
图1 集中式事件触发机制下系统的轨迹Fig. 1 The trajectory of the system under centralized event-triggering mechanism

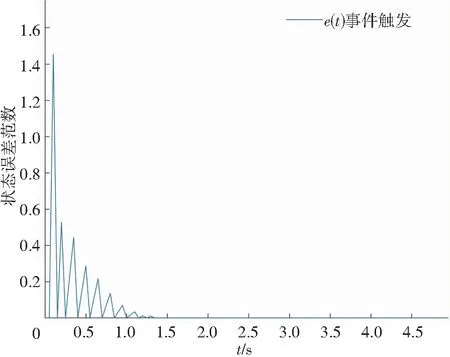
图2 集中式事件触发机制下系统状态误差变化Fig. 2 Changes of system state errors under centralizedevent-triggering mechanism

对于分布式事件触发式(2)中,参数的值分别取为:α=30,σ1=0.5;σ2=0.5;σ3=0.5;σ4=0.5;智能体的状态轨迹如图3所示,为了方便描述系统误差状态变化选取智能体3的图像,如图4所示。

图3 分布式事件触发机制下系统的轨迹Fig. 3 The trajectory of the system under the distributedevent-triggering mechanism

图4 分布式事件触发下智能体3的状态误差变化Fig. 4 Changes of state errors of Agent 3 triggered by distributed events

可以看出系统式(1)在两种协议下,都能实现一致性。

5 结论与讨论

研究了有向网络拓扑下,基于事件触发的非线性动态的多智能体系统一致性问题。考虑到系统自身和网络宽带的资源是有限的,为了有效利用资源,降低系统控制过程中的资源消耗问题,提出事件触发控制协议,设置了两种不同的一致性控制协议,假设智能体的通信拓扑是强连通的,设计一种集中式的控制协议,即系统中的每个智能体都具有相同的触发时刻,控制器不在连续的更新状态,只在离散时刻更新状态,利用矩阵理论和代数图论等相关知识,得出系统在集中式控制协议下实现一致性的充分条件。其次讨论分布式控制协议,即智能体只需要利用邻居智能体和自身的信息,将集中式的结论推广到分布式的一致性协议上,得出在分布式协议下系统可以实现一致性,最后通过数值仿真,也验证了所提理论的正确性。

下一步工作就是在此基础之上讨论动态事件触发的一致性问题,即触发条件不仅可以利用当前智能体的状态和测量偏差的状态,还与智能体触发前的智能体状态建立联系,使得设计的触发条件更加精确。其次考虑智能体之间不仅有协作还有竞争关系,即讨论二分一致性问题,使所构建系统更加贴近生活实际,最后,再进一步考虑高阶多智能体系统领导跟随一致性问题。