基于双目立体视觉系统的测量研究

闫小宇,陆凡凡,葛芦生,伍孟涛,刘 彬

安徽工业大学 电气与信息工程学院,安徽 马鞍山 243002

1 引 言

计算机视觉的研究目的是让二维图像来识别三维空间信息的能力。立体视觉技术在众多计算机视觉方法中具有很重要的地位,它对场景处理的形式类似于人类双目对眼前所看内容处理形式,具有简单性、可靠性、灵活性等特点,可以在许多不利条件下对景物的立体信息进行测量,可以不需要接触、自动、在线的检测。视觉测距是一个很重要的分支,不同于超声波、激光是通过计算发射源接收和发射过程所消耗时差进行测量距离的主动测距,主动测距速度快,操作简单,但是在一些恶劣的环境下如光照、噪声等这些主动测距的方法效果就逊色很多。所以对于一些需要一定条件下进行测距的应用主动测距就受到很大的限制。双目测距是通过对目标物自身的光信号进行反射到摄像机内来实现测距,是一种被动的测距方式。以其结构简单、效率高、精度高、便于使用等诸多优点用于导航、非接触测量、工件定位等诸多领域。对于双目视觉测量系统,摄像机标定、立体校正、立体匹配是核心工作[1]。其中立体匹配是整个测距系统最难也是最关键的一部分。立体匹配算法常见的有全局立体匹配和局部立体匹配算法。全局匹配是考虑图像上对应全部像素点,所以其效果好准确性高,但对于计算量是很大的,耗时较高,经典全局立体匹配算法有动态规划算法(Dynamic Programming,DP)[2]、置信传播算法(Belief Propagation,BP)[3]、图割算法[4](Graph Cuts,GC)等算法,全局立体匹配算法得到精度较高的视差图,但算法需要的计算过程较复杂。而对于局部匹配是通过选定一个合适的窗口,通过遍历所选窗口内的像素点进行匹配,匹配方式遍历整个图像像素的一部分,计算量较少,速度快,适用于大多数应用场景,常见的立体匹配算法有绝对误差之和(SAD)、绝对误差(AD)、跨尺度代价聚合算法[5]等。许威等[6]将MATLAB及Open CV应用在双目测距系统中搭建了测距系统。汪珍珍等[7]通过搭建的双目测距系统并使用SAD算法实现了对得到图像的匹配。

对于双目立体视觉测距系统大致可分为:图像采集、立体标定、立体校正、立体匹配和测距。由张法[8]来实现标定,对于摄像机的标定可以使用MATLAB工具箱实现。得到的标定参数再导入OpenCV。利用BM匹配算法完成立体匹配得到相应的视差图,最后利用相似三角形理论计算三维信息。

2 测距原理

双目视觉和人的视觉相似,人的视觉中双眼判断目标物体的距离是由双眼对目标物体所表现图像的不同决定的,两台摄像机通过多方位进行旋转或平移对相同的视场进行采集,再从采集到的图像得到真实空间对应的视差,最终可以获取空间点的三维坐标值[9]。

双目摄像机系统模型如图1所示。P(XC,YC,ZC)是空间中任意一点,Ol、Or分别对应摄像机的左右光心,左右光心所在的成像平面进行对齐。Pl(xl,yl)和Pr(xr,yr)是P点的投影点。焦距f,基线T。要想得到P点的三维坐标,只需求得P点在Ol中的投影点Pl及在Or中的投影点Pr的坐标。视差为左右投影点之间的横坐标的差值,即视差d=xl-xr。由点Ol、点Or、点Pl、点Or以及点P这5个点共面[10]。则根据三角形相似原理可得式(1):

图1 双目视觉测量原理Fig.1 Principle of binocular vision measurement

(1)

由视差d=xl-xr可求出摄像机坐标系下点P的坐标:

(2)

由式(2)可知对于摄像机的坐标系和摄像机参数以及视差有很紧密的联系,对于所要得到的三维空间信息就包含在这视差中。求取摄像机参数f和T在标定环节,图像视差值获取在立体匹配环节。即测距的精度[11]离不开摄像机标定与匹配环节。

3 摄像机参数标定

3.1 摄像机标定原理

在立体视觉系统中,由拍摄的图像可获得景物所对应的轮廓、定位等信息。对于未知的摄像机方位,可由标定来得到图像内的点与映射到三维空间点对应关系。为了得到目标物体的信息,需要将像素坐标系O1-uv,图像坐标系O0-xy,摄像机坐标系OC-XCYCZC,世界坐标系OW-XWYWZW进行转换。摄像机标定是将空间三维坐标点和图像二维坐标点对应。摄像机标定的基本思想是利用一些已知点、线或面在图像坐标和三维空间坐标,解出转换矩阵中对应的内外参数,可得到投影矩阵M。

由于近些年摄像机标定技术发展很快,针对不同的摄像机模型,学术界提出了一系列经典的标定算法有:直接线性变换算法(DLT),自标定法,张正友棋盘格标定等,通过对以上标定方法仔细研究,最终用张法实现标定。方法使用的是针孔模型。传统的标定方法对于标定物有很高的精度要求,而张法对于标定物的要求就相对简单,只需要一张标准的棋盘格,与自标定法不同的是张法标定的精度有很大的改善。因此张法标定广泛地应用于计算机视觉领域[12]。

O1-uv系的横坐标u和纵坐标v分别表示图像所在的列与行,单位为像素。O0-xy系的单位一般为mm,而像素在O0-xy系中并没有实际的物理单位。O1-uv系所在的u轴和v轴分别平行O0-xy系的x轴和y轴。像素图像之间坐标转换如式(3)所示:

(3)

其中,(u,v)为像素坐标,(x,y)为图像坐标。

摄像机与OC-XCYCZC系的中心重合,OC-XCYCZC系的水平轴XC与垂直轴YC分别平行O0-xy系的x,y轴,z轴垂直且朝着像素平面,O0-xy系的原点位于z轴相交像素平面处,对于两坐标系之间的距离为摄像机的焦距f。

OW-XWYWZW系旨在统一空间中的所有坐标进行表示。根据应用场景的不同,OW-XWYWZW系有不一样的表示方法。对摄像机进行标定时,将标定板的某个角点视为OW-XWYWZW系。对于OW-XWYWZW系的XW,YW,ZW轴并不是与其他坐标轴平行的而是存在一定的角度。透镜的系与OC-XCYCZC系之间存在如式(4)所示的关系:

(4)

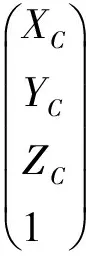
(5)

改为齐次坐标和矩阵形式如式(6)所示:

(6)

M1M2XW=MXW

(7)

其中,M为3×4的投影矩阵,M1为内参矩阵,M2为外参矩阵。dx,dy是尺度因子,u0,v0图像中心坐标。

透镜的畸变[13]主要分为径向畸变和切向畸变(径向畸变张法不考虑四阶以上的情况)。径向畸变可能是工艺制作过程所带来的误差。畸变程度与距离透镜边缘成正比。矫正前后坐标为式(8)所示:

(8)

切向畸变可能是摄像机的本身或安装所带来的误差。切向畸变矫正前后的坐标为式(9)所示:

(9)

其中,x,y是图像坐标中无畸变的,x′,y′是去除畸变后的图像坐标,k1,k2,p1,p2,k3是畸变系数与式(7)中参数f,dx,dy,u0,v0一起形成内参数。

3.2 摄像机内外参数标定

实验使用Matlab工具箱进行内外参数标定,为了标定实验的精确性,实验分别在摄像机距离标定板300、400、500、600、700 mm处采集不同位姿和角度的图像进行摄像机标定确定最终的参数。

3.2.1实验环境

实验所用的双目摄像机型号为zed,视频采集图像分辨率为1 280×720(像素)。标定图案由8列6行方块组成,每个方块实际大小为20 mm×20 mm,角点数为7×5。两摄像机平行放置,基线距离约为120 mm,图像分辨率为1 280×720像素。计算机配置为Intel(R)Core(TM)i5-10200H CPU@2.40GHz 2.40 GHz处理器,16 G内存,NVIDIA GeForce GTX 1650显卡。实验硬件组成如图2所示。

图2 实验硬件组成Fig. 2 Experiment hardware

3.2.2Matlab工具箱标

使用Matlab工具箱进行标定具体标定步骤如下:

(1) 固定好双目摄像机zed,同时拍摄不同位姿的图像,实验取16幅图像进行标定,通过Matlab命令指令calib_gui分别读入左右摄像机得到标定图像如图3所示,其中,图3(a)为左摄像机标定图,图3(b)为右摄像机标定图。

(a) 左摄像机标定图

(2) 读入图像完成后操作工具箱中的Extract grid comers对每组图像提取标定点(方格交叉点)的图像坐标,图4为左右摄像机获取的第一幅图像提取标定的结果(得到7×5个标定点),其中,图4(a)为左摄像机标定结果图,图4(b)为左摄像机标定结果图。图5为左右摄像机其他的15幅图像提取标定点后的结果。

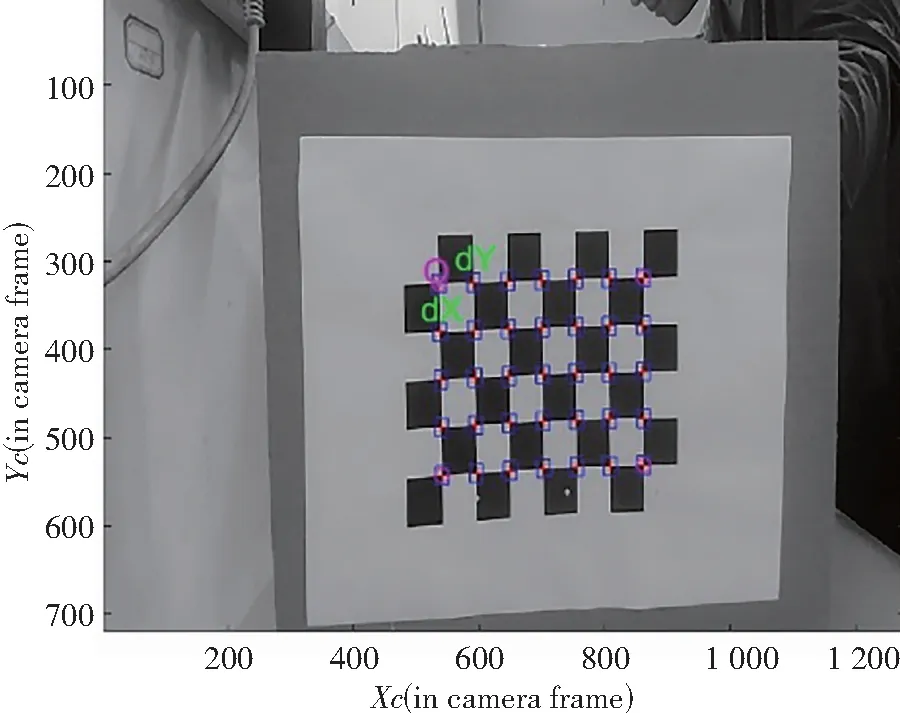
(a) 左摄像机标定点结果图

图5 左右摄像机剩下15幅图提取标定点结果Fig. 5 The remaining 15 images of left and right cameras to extract the calibration points

(3) 完成标定点提取后,点击工具箱中的Calibration键,就可以单独对左右摄像机进行标定,得到对应的摄像机内参数。

(4) 对双目立体视觉系统而言,外参数可以是左右摄像机各自相对世界坐标系的,使用更多的是左右摄像机之间的关系。当有了各自相对于世界坐标系的外参数之后,便很容易得到左右摄像机之间的位置关系。通过使用工具箱输入的指令stereo_gui分别读取左右摄像机参数进行双目摄像机标定即可外参数旋转矩阵R和平移矩阵T。

4 立体校正与匹配

双目视觉主要用于测距,在理想的双目系统下通过视差代入距离公式可以将距离求出,而实际的双目系统获取的两张图像不在共同的平面上,这对于测距带来了很大的不便。所以,要进行立体校正。校正是为了将摄像机得到的图像校正到同一面上,同一个投影点落到图像平面的像素横坐标要相同,这样就实现了降维,为立体匹配降低了难度[14]。

实验将Matlab工具箱测出的内外参数导进OpenCV中,利用cvstereoRectify函数来立体校正,图6为立体校正前后左右图像对。校正前畸变较严重,校正后相同的点基本在同一条线上[15]。

图6 立体校正前后左右图像对Fig. 6 The left and right image pairs before and after stereo correction

立体匹配是找到不同视点对应的同一个景物中的投影像素之间的对应关系[16]。根据图像所表达的基元不一样大致可以分为:区域匹配[17]方法和特征匹配方法[18]。

(1) 区域匹配方法。方法根据假设不同的图像匹配区域有灰度相似的分布,对图像进行小区域划分,再对差异图像间划分适当的小区域图像的灰度值相似性进行计算,最后将不同图像之间的区域匹配联系起来。方法定位的精度很高以及有稠密的视差区域,是由于方法对图像像素直接进行匹配,与特征检测精度以及密度无关。灰度信息是匹配的关键,导致匹配会对景物表面的结构、光照强度、成像几何很敏感,当出现图像本身纹理不够多或图像中存在障碍物遮挡一些区域使用该方法效果不够理想。

(2) 特征匹配方法。方法是对图像中特殊的点或其他特殊的基元进行提取灰度,在使用图和表的形式表达这些基元间的关系,可以将图像间的匹配问题转换为图和表之间的对应问题。特征匹配是有选择匹配景物特殊的特征,而不是直接通过灰度进行匹配,更多的选择景物的特殊结构来进行匹配。匹配方法具有对景物所处环境不敏感、精度高、稳定性好喝匹配速度快等优点。

实验中使用opencv中的SAD(Sum of absolute diffe-rences )块匹配算法完成左右图像对的匹配。基本思想:将每个像素对应数值之差的绝对值求和,据此评估两个图像块的相似度来判断图像是否匹配[19]。基本流程如下:

① 构造一个窗口并覆盖左图像,计算出窗口覆盖区域内的所有像素点灰度值;

② 再用同样大小的窗口覆盖右图像并计算出覆盖区域的像素点灰度值;

③ 用左边窗口灰度值减去右边窗口灰度值,并计算出像素点灰度值差的绝对值之和;

④ 滑动右边图像的窗口,重复③和④的处理。

⑤ 找到这个范围内SAD值最小的窗口,即找到了左边窗口内图像在右图像中最佳匹配的像素块。

完成匹配就可以生成视差图,图7是左摄像机拍摄的图像和对应的视差图[20]。

图7 左摄像机拍摄的图像和对应视差图Fig. 7 The image taken by the left camera and the corresponding disparity map

当知道某一点的视差和摄像机参数,可以计算物体的深度[21]。

5 系统标定结果分析及验证

5.1 标定结果

实验分别在摄像机距离标定板300、400、500、600、700 mm处,左右摄像机各拍摄16幅图像,按照之前叙述标定的方案进行标定,得到左右摄像机内部参数,以及根据罗德里格斯转换定理(Rodrigues)可得左右摄像机的相对几何位置即旋转向量rec和平移向量t,由于张法忽略径向畸变的四阶以上的畸变量所以得到k3为0结果如表1、表2、表3所示。

表1 左摄像机内部参数Table 1 Internal parameters of the left camera

表2 右摄像机内部参数Table 2 Internal parameters of the right camera

表3 左右摄像机相对外部参数Table 3 Relative external parameters of left and right cameras

由表1—表3的结果可以看出,在不同位置的标定下,无论是内部参数还是外部参数都存在不同,由表3中参数tx(x轴上两个摄像镜头的偏移量)均值的绝对值为119.337,而zed双目摄像头光心之间的实际长度为120mm,说明标定的参数在忽略工艺误差下较为准确。下面分别给出了其中一个位置得到的左右摄像机和双目摄像机外部参数的场景模拟图。图8为摄像机外部参数场景图,图8(a)为左摄像机外部参数场景图,8(b)为右摄像机外部参数场景图。图9为左右摄像机外部参数场景图。

(a) 左摄像机外部参数场景图

5.2 实验验证

实验的目的是要测量出目标物到摄像机光心之间的距离,将被测目标物分别置于离光心200 mm到3 000 mm处。根据摄像机标定的各项参数和式(7)可得到目标的空间坐标值,再根据距离式(10)求出目标物与摄像机光心的距离。试验是通过编写C++程序在同一平面上通过鼠标点击视差图中亮度大的点来确定选定点到摄像机光心的距离。测得6组目标物距离摄像机光心400 mm的测量结果如图10所示以及测量值如表4所示。

表4 目标物距离像机光心400 mm处测量值Table 4 The measured value of the target object at a distance of 400 mm from the optical center of the camera

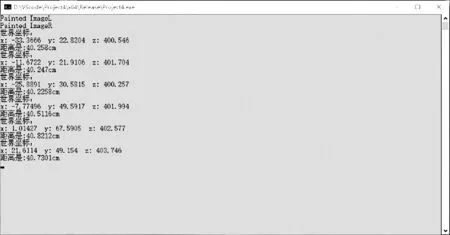
图10 测量结果图Fig.10 Measurement results

(10)

其中,L测为测量值,XW,YW,ZW为被测目标物的三维空间坐标值。

将测量序号1组的数据代入式(10)得到:

402.580 684≈L测

说明代入的公式和测量数据是准确的。

将每个测量点所测量出的6组数据进行求均值作为最终测量值再与该测量点真实值进行比较得到误差,再根据相对误差的趋势来判断该系统的精度的高低以及满足精度要求的测量距离范围。得到的实验数据如表5所示。

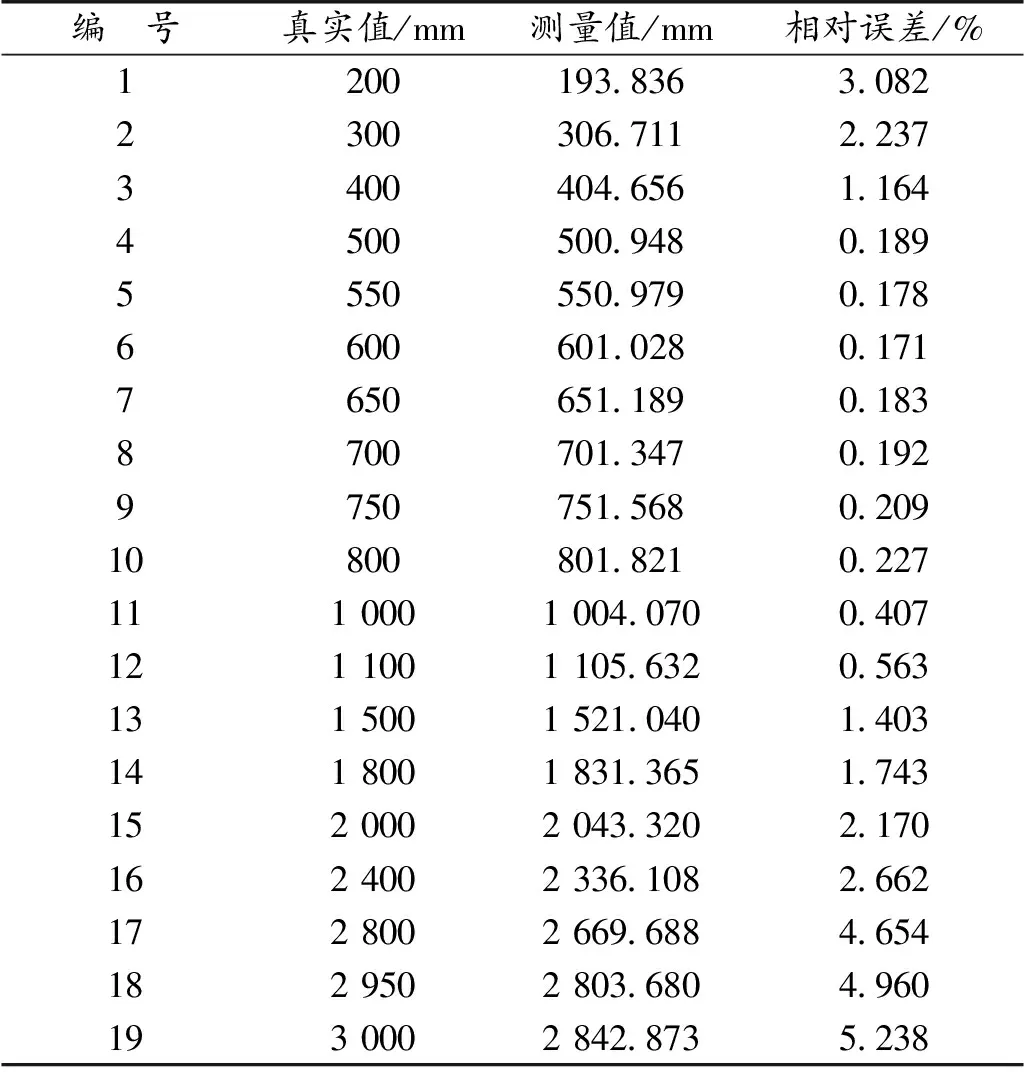
表5 实验结果Table 5 Experimental results

实验结果表明:由于视差估计算法的精度,双目摄像头基线和焦距的大小有限,以及双目摄像机的分辨率会影响实验测量精度,当被测物体距离较近时,就会有对焦模糊甚至虚化等现象,图像采集的效果差,使立体匹配精度降低,所以在实测距离较近情况下,测距精度相对较低,在实测距离超过一定范围且随着测距增加,测量误差也增加,测量精度也随之降低。通过测量误差和距离的对比,在2 950 mm以内,误差不超过5%,满足实验要求。

6 结 论

实验基于双目立体视觉测距原理,对立体标定、立体校正、立体匹配以及实验结果进行了研究,通过Matlab完成了双目摄像机的标定并得到了双目摄像机各项参数,并在VS2017坏境与opencv 3.4.7结合下进行测距实验,实验结果表明被测物距离摄像头光心500 ～700 mm这一范围时,实测距离和实际距离相对误差百分比在0.171%～0.192%之间,测量精度较高,且实测距离在2 950 mm内实验误差小于5%满足实验精度要求。误差主要来自摄像机本身参数误差、标定过程中误差和光线纹理的影响。这些误差给立体匹配带来一定难度,会导致测量精度会降低。