南瓜型超压气球展开稳定性研究

卜亚楼,蔡 榕,杨燕初,张向强

(1. 中国科学院大学航空航天学院,北京 100040;2. 中国科学院空天信息创新研究院,北京 100094)

1 引言

零压气球自20世纪50年代早期产生以来,作为一种高效费比的飞行器为科学研究做出很大贡献。但零压气球由于自身结构的特点,面临着不可避免的局限性——无法长航时飞行。南瓜型超压气球作为一个封闭的气球相比于零压气球拥有较高的内压力,其球体体积不受昼夜温差的影响,因此驻空高度比较稳定,驻空时间显著延长。南瓜型超压气球以其显著的优势获得了世界各国的青睐。美国NASA在2016年的ULDB(Ultra Long Duration Balloon)项目中采用南瓜型超压气球实现了中维度区域46天的长航时飞行[1]。中国科学院在2017年9月开展了首次南瓜型超压气球的飞行试验,获得成功。然而,南瓜型超压气球被发现存在潜在的展开不稳定性问题。

1984年,J.Nott[2]在对自己设计的大型南瓜型超压气球充气时发现,气球的几幅球膜隐藏在球体内(如图1);继续加压,其形状基本保持不变。Nott在移除其中两幅球膜后仍无法完全展开,最后在移除四幅球膜后成功展开了。但在较高的压强下,气球仍会出现扭曲状态。南瓜球的展开不稳定性问题首次被发现。

图1 “奋进号”气球的扭曲

在之后的几年中,美国、日本、瑞典等国家均报道了类似现象。因此,南瓜球稳定性的问题是客观的。针对这种现象,研究人员采用许多数值方法来模拟失稳形态,以探索失稳形成的原因,并寻求一个具有更高展开稳定性的形状设计。

Calladine[2]从几何稳定性的角度开展研究。通过将球膜的几何刚度与欧拉梁的抗弯刚度进行类比,得到关于球膜幅数n与凸出角α之间的稳定性判据,并将此判据绘制成曲线图。但在随后的研究中发现,Calladine的结论更适用于按照恒定凸出角度(constant bulge angle, CA)设计的气球。Smith和Rainwater[3]认为按照恒定凸出半径(constant bulge radius, CR)设计的气球展开稳定性更好。因此,Smith和Rainwater进一步研究了恒定凸出半径气球的稳定性,并获得与Calladine相似的曲线图。其中横坐标是球膜幅数n,纵坐标是弧长s与弦长c的比值s/c,这是一大进步。Schur[4]和他的同事通过开展地面试验来研究是哪些设计特征导致了展开缺陷问题。Schur推断,过量的幅宽可能导致展开不稳定,并指出按照恒定凸出半径设计的气球更有利于展开。Baginski[5-9]等人通过能量最小原理计算平衡构型。其中的总能量包含气体的静水压势能、球体的重力势能以及球膜的应变能和加强筋的应变能。他们发现如果理想的循环对称展开形状是不稳定的平衡构型,那么气球在正常上升过程中不会达到循环对称的形状。然而,他们无法对气球进行合理设计使其稳定展开。Pagitz和Pellegrino[10]等人认为南瓜球扭曲的稳定平衡构型是一个涉及平衡路径分叉屈曲的问题,他们通过求解整体切线刚度矩阵的特征值和特征向量来研究失稳压强和失稳形态,其中Xu和Pellegrino[11,12]利用ABAQUS/Standard通过特征值屈曲分析,预测了气球的临界失稳压强和相应的屈曲模态。Deng[13]采用显式动力学有限元软件计算了部分充气气球的平衡问题。其中考虑了球膜材料的非线性行为,对正交各向异性粘弹性材料进行了分析和建模,并基于变泊松比的起皱准则模拟了薄膜的起皱行为,获得的仿真结果与试验有很好的一致性。日本科学家Izutsu提出一种新颖的设计方式。通过在普通南瓜球的赤道处加入相同截面的圆柱体,形成一种所谓的“tawara”形气球[14]。通过地面充气展开试验和数值分析证明了这种设计方法有助于提高球体展开稳定性,但这种形状设计增大了南瓜球的气动阻力,并非目前南瓜球的主流设计方式。

已有数值研究多在成型的南瓜球上通过加压进行分析,忽略了成型前的膨胀过程,且研究主要针对南瓜球几何形状参数对稳定性的影响,关于材料属性对稳定性的影响研究较少,具有一定的片面性。本文通过采用控制体积法对南瓜球进行充气展开数值模拟并开展地面充气试验,获得南瓜球的失稳过程和失稳形态。综合考虑几何形状参数和材料属性对稳定性的影响,通过将特征值屈曲分析与气球囊体环向应变变化相结合的方式探索影响南瓜球稳定性的因素。

2 超压气球建模

本文针对三种不同几何参数的超压气球模型进行分析,其三维模型图如图2所示。

图2 超压气球三维模型示意图

模型1的直径为30m,分膜幅数为120幅;模型2的直径为20m,分膜幅数为70幅;仅增大模型1鼓包的凸出半径,获得模型3。其中,模型1和模型2是中国科学院用来试验的测试气球。气球的详细几何参数见表1。

表1 超压气球几何参数

图3显示了赤道平面处相邻加强筋之间球膜的截面形状。气球的加强筋位于相邻两幅球膜的焊缝处,气球的赤道半径用R表示。对于n幅球膜的情况,赤道对角为θ=2π/n。其中s是鼓包的弧长,c是弦长。r是鼓包的半径,α是鼓包凸出角。

图3 赤道平面处的凸出截面形状

根据几何关系,鼓包弦长可用赤道半径和赤道对角表示

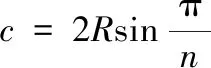
(1)

此外弦长也可用凸出半径和凸出角表示

(2)

根据式(1)和式(2),可得出赤道半径与圆弧半径的关系为

(3)

其中鼓包弧长为

s=αr

(4)

由于鼓包的圆弧与凸出角或凸出半径有关,目前超压气球的设计主要采用两种方法,一是凸出半径沿子午线保持恒定的凸出半径设计,二是凸出角沿子午线保持恒定的凸出角度设计。祝榕辰[15]证明了恒定凸出半径的设计方法能使球膜表面的应力分布更加均匀;文献[4]从展开稳定性的角度论证了恒定凸出半径设计的气球具有更好的稳定性。因此,恒定凸出半径设计方法得到了较广泛应用。本文所采用的三种模型均按恒定凸出半径设计。根据以上几何参数及几何关系完成建模。

气球球膜和加强筋对其所用的材料有多种特性要求,随着材料科学的发展,球膜和加强筋的特性在不断改善。线性低密度聚乙烯以其优越的性质取代了以前的低密度聚乙烯作为球膜材料;PBO(p-phenylene benzobisoxazole)以其优越的力学性能、热稳定性和优异的强度重量比被选择作为加强筋的材料。目前,世界上几个开展高空气球项目的国家均在采用这种材料,例如ULDB项目。具体材料属性如表2所示。

表2 材料属性

3 超压气球充气展开

超压气球的扭曲形状是在上升过程中由于氦气膨胀对球膜的作用造成的。为了研究膨胀展开过程中超压气球的失稳现象,有必要构建未充气状态下的模型,并在此基础上模拟充气膨胀展开过程。以往研究人员对充气管、气囊[16]、空间充气天线等充气结构的研究为本问题提供了很好的思路和方法。

3.1 充气展开数值仿真

基于显式动力学软件LS-DYNA开展充气展开数值仿真。针对超压气球模型1,首先利用完全重启动方法获得重力场作用下的气球形态,即悬挂的、未充气的初始模型(如图4);在此基础上使用控制体积法(Control Volume,CV)进行充气展开模拟。关于控制体积法的原理介绍详见文献[17],具体参数设置在此不再赘述,仅给出仿真结果以说明问题。随着充气模拟的进行,气球缓慢膨胀。在基本成型、直至超压后出现四上四下的形态(如图5);继续充气,出现了局部塌陷(如图6)。

图4 重力场作用下的初始状态

图5 四上四下形态

图6 气球局部塌陷

3.2 地面充气试验

作为飞行试验的预试验,2019年6月,中国科学院针对模型1和模型2开展了地面充气试验。首先从顶部法兰盘向气球充入氦气,以提供部分自由浮力,随后通过风机充入空气。在整个充气测试过程中对气球底部的压差进行监测。随着充气的进行,气球逐渐膨胀,模型1在压差达到30Pa时呈现扭曲状态;继续充气,内外压差继续增加,但球体仍不能展开成型。并形成了上下凸出(图7a)、S形裂缝(图7b)和局部塌陷(图7c)三种状态,即整体失稳和局部失稳。这种现象表明,模型1的扭曲状态即为最终的稳定平衡状态。

图7 不同失稳状态:整体失稳(a)和局部失稳(b、c)

对模型2进行同样的充气操作。随着充气的进行,气球稳定膨胀展开,直至成型(如图8);继续充气,气球超压。在底部压强约为900Pa时,球膜材料失效,气球出现裂口。整个充气过程中气球没有表现出任何失稳现象。

图8 超压气球完全展开成型

3.3 结果对比分析

观察充气展开数值仿真结果可以发现,初始悬挂状态下球膜存在大量折叠和褶皱,球膜之间相互接触。在气球基本成型后,褶皱消失,多余材料在气球的较低区域形成折叠,球膜的接触区域主要存在于上下凸出的四个波峰之间;继续充气,四个凸起的波峰合并成一个,多余薄膜材料被挤压导致局部塌陷。此时,整个气球除去塌陷区域外基本是光滑的、均匀的。对比地面充气试验可以发现,塌陷区域约有24幅球膜,仿真结果与试验气球相比表现出显著的相似性。因此,充气展开数值分析与试验气球之间不稳定模式的相关性是清楚的。此外,对比两个模型的地面试验结果可以证明,气球展开稳定性与其结构设计直接相关。

针对充气展开过程中出现的对称的四上四下现象,初步判断为南瓜球的一种屈曲模态。由于屈曲理论具备较完善的理论体系,在处理稳定性问题上比较成熟,因此,把研究重点转移到屈曲分析上。从后面的结果可以看到,充气展开过程出现的四上四下形态是特征值屈曲模态的一种情况,局部塌陷是一种后屈曲形态。

4 超压气球屈曲分析

4.1 特征值屈曲分析理论

结构的失稳可分为极值型失稳和分支型失稳[18]。工程中大量稳定性问题属于极值型失稳,但由于分支型失稳在数学上容易作为特征值问题处理,力学上表达明确,并且它的临界载荷又近似地代表相应的极值型失稳载荷的上限,因此多转化为分支型失稳问题来处理。超压气球扭曲的稳定平衡构型可看作是一个涉及平衡路径分叉屈曲的问题,属于分支型失稳。基于有限元模型的分支型失稳的研究方法又称为特征值屈曲分析。

特征值屈曲分析是一种线性摄动分析,它基于小位移线弹性理论,通过提取使线性系统刚度矩阵奇异的特征值来获取结构的临界失稳载荷和失稳模态[19],显著简化了问题的规模,从而提高了计算效率。结构的静力平衡方程如下

[K+λKG]{u}={Q}

(5)

式中,[K]为结构的弹性刚度矩阵;[KG]为结构的几何刚度矩阵;λ为特征值;{u}为结构的模态特征向量;{Q}为作用在结构上的载荷。

平衡方程(5)失稳的条件是方程存在奇异性,即等效刚度矩阵的行列式的值为零。

|K+λI[KG]|=0

(6)

特征值屈曲分析即为求解式(6)的特征值,所求得的特征值即为临界载荷系数。将某一阶屈曲模态特征值与施加的载荷相乘,就得到该阶模态下结构的特征值屈曲临界载荷。{u}为屈曲模态位移,它预测了结构可能的失效形式。

4.2 有限元建模

超压气球的线弹性各向同性球膜采用M3D4膜单元建模,加强筋PBO采用桁架单元T3D2建模。赵荣[20]证明了加强筋和膜单元之间采用共节点约束与采用滑动摩擦约束对球膜承力并无很大差别。因此,为了建模简单起见,本研究采用共节点约束。顶部法兰盘和底部法兰盘均为全约束。此外,为了获得较好的网格质量,本分析中没有构建法兰盘部件,而是以桁架单元代替法兰。这样做可以提高计算的收敛性,而不影响计算结果。

4.3 特征值屈曲结果分析

计算得到模型1和模型2的前八阶屈曲压强和屈曲模态。图9显示了模型1前四个不同特征值对应的屈曲模态。需要注意的是屈曲模态{u}为归一化向量,最大位移分量为1.0,这并不代表在临界载荷下变形的实际大小,但其能够表明结构的可能失稳模式。

图9 前四个屈曲模态的总位移等值线图

事实上,每一个特征值所对应的两个屈曲模态是相同的。不同的是,相同特征值下的两个模态为绕竖直轴旋转约15°,如图10所示。

图10 具有相同特征值的两个屈曲模态俯视图

由图9可以看到,屈曲模态表现出整体对称的n上n下形态。表3和表4分别给出了模型1和模型2每阶特征模态所对应的临界屈曲压强。高阶模态对应更大的n值;随着n的增大,需要更大的临界压强通过分叉加载点,但临界压强与n并非简单的线性关系。当n不超过4时,相邻特征压强相差较小;当n大于4时,相邻特征压强表现出显著的差距。

表3 模型1对应于屈曲模态的屈曲压强

表4 模型2对应于屈曲模态的屈曲压强

对比表3和表4可发现,在相同的材料属性下,模型1和模型2在屈曲模态形状上表现出基本相同的规律。不同的是,模型1的临界屈曲压强远小于模型2。这说明模型1极易失稳,模型2难以失稳。这与试验结果是相符的(试验中,模型1在30Pa的压强下表现出无法改变的扭曲形状;模型2直至材料失效都没有表现出扭曲现象)。由此得出结论:超压气球几何参数设计对展开稳定性有直接影响。

5 灵敏度分析

5.1 材料属性对稳定性的影响

虽然在本研究中只针对表2中的材料属性进行了详细研究,但设计人员需要知道不同的材料属性对展开稳定性的影响。此外,研究材料属性对稳定性的影响也有助于探索失稳原因。现针对模型2的球膜弹性模量、泊松比、加强筋刚度以及球膜厚度分别在变化±20%、±40%时计算其屈曲压强。图11显示了其计算结果。

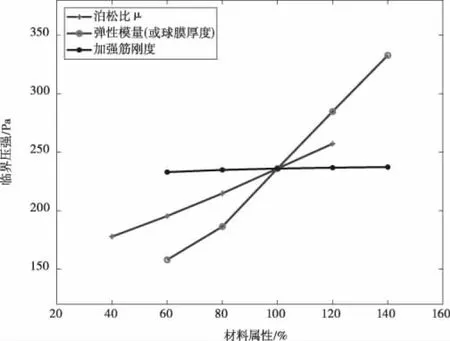
图11 临界屈曲压强随材料属性变化曲线

对比图11中的曲线可以发现,球膜弹性模量(或球膜厚度)对应的曲线具有最大的正斜率,说明临界屈曲压强对薄膜的抗拉刚度Et(弹性模量或球膜厚度)最敏感。抗拉刚度增加20%,临界屈曲压强增加28%。这主要是由于较大的抗拉刚度会导致较小的环向应变,从而造成球膜的凸出角减小,环向余料减小,临界屈曲压强增大。此外,球膜弹性模量和球膜厚度对临界屈曲压强的影响是相同的。这是由于膜单元不能承受弯矩,仅有抗拉刚度Et。在弹性模量和厚度变化相同的百分比时,球膜的环向应变变化是相同的,因此屈曲压力相同。

改变薄膜的泊松比可以得到类似的规律。根据材料的应力应变关系

(7)

(8)

其中,环向应变为εφ,径向应变为εθ。环向应变和径向应变由泊松比耦合,增大泊松比,环向应变减小,从而造成凸出角减小,环向余料减小,屈曲压力增加。泊松比增大20%,临界屈曲压强增加10%。Pagitz和Pellegrino进行了类似的分析,其结果与上述讨论基本一致。

增大加强筋的刚度也会增加临界屈曲压强。但临界屈曲压强对该参数的变化不敏感,这是由于加强筋刚度对球膜的径向应变影响较大,对环向应变的影响不明显。

为了进一步证实气球稳定性与环向应变有关的事实,类似屈曲分析,对材料属性进行相同规律的变化,进行静力学分析。对模型2施加500Pa内压,获取球膜赤道某一单元的环向应变和径向应变值,其环向应变云图和径向应变云图如图12所示。应变值见表5和表6,并将其绘制成曲线图,如图13所示。

表5 应变值随弹性模量的变化

表6 应变值随泊松比的变化

图12 环向应变云图(a)和径向应变云图(b)

图13 环向应变随材料属性变化曲线

通过观察环向应变可以发现,随着弹性模量和泊松比的增大,环向应变逐渐减小。其中弹性模量变化对应的曲线有最大的斜率绝对值,这与屈曲压强对薄膜刚度(弹性模量或球膜厚度)变化最敏感的结论是吻合的,再次印证稳定性与环向余料有关的结论。

5.2 法兰半径对稳定性的影响

将模型2的法兰半径减小一半,计算得到的屈曲压强与原模型2相比见表7。

表7 变法兰半径的屈曲压强对比表

减小法兰半径屈曲压强降低,展开稳定性降低。这可以解释为:将气球稳定性看做是压杆稳定性问题。减小法兰半径,相当于使压杆变得细长,稳定性降低;增大法兰半径相当于使压杆变得短粗,稳定性增加。

5.3 s/c值对稳定性的影响

以赤道平面为例,旋成体欧拉球[21]可看作是南瓜型超压气球凸出半径增大至欧拉球半长轴的极限情况,亦即不存在鼓包。旋成体欧拉球不存在失稳现象。据此可以推断,在不改变球膜幅数的情况下,减小s/c值,即增大凸出半径,屈曲压强会增大,展开稳定性提高。事实上,早在2004年Smith和Rainwater已得出了按照恒定凸出半径设计的超压气球其球膜幅数n和s/c与稳定性的关系图。

现对模型1的几何参数做出如下改变,如图14所示。模型1的s/c为1.40,n为120,位于极限曲线图的上方且偏离极限曲线较远,即不稳定区。根据式(1)～(4),保持n不变,当s/c的值减小到1.057时,凸出角为66.04°,凸出半径为0.7268m,获得模型3。此时,模型3变化到稳定区。做出这样改变的赤道截面几何形状对比图如图15所示。显然,模型1的鼓包变小了。

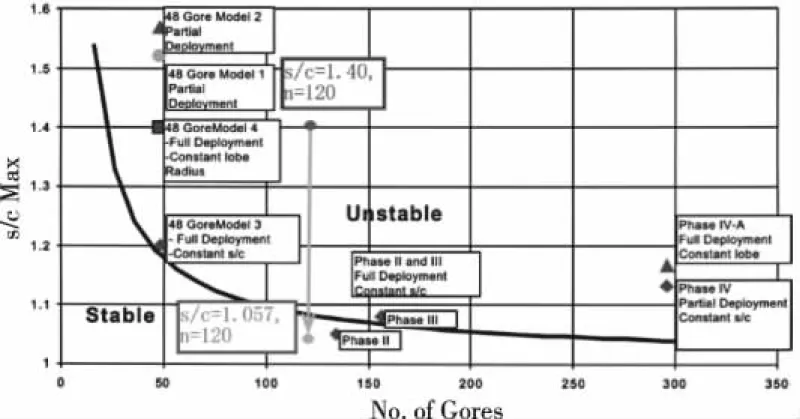
图14 恒定凸出半径设计下稳定性极限曲线[4]

图15 模型1和模型3的赤道平面鼓包截面对比

根据稳定性与环向余料有关的判断,模型3的环向余料低于模型1。因此,位于稳定区的模型3其稳定性应当优于模型1。分别对两个气球进行特征值屈曲分析,得到的临界屈曲压强值见表8。可以看到,模型3的临界压强值远远高于模型1,即模型3是稳定的。这说明减小s/c的值有助于提高气球稳定性,也印证了Smith和Rainwater得出的极限曲线图具有一定的参考意义。

表8 变s/c的屈曲压强对比表

6 结论

本文通过对南瓜型超压气球进行充气展开数值模拟、特征值屈曲分析和地面试验得到以下结论:

1)南瓜型超压气球几何参数设计不合理时,随着压差的增大,会呈现出失稳形态。并且失稳过程优先出现整体失稳,继续增大压差,表现出局部失稳。

2)材料属性对展开稳定性有影响。其中球膜弹性模量、泊松比和厚度在变化+20%时,临界失稳压强分别变化+28%、+10%和+28%。临界失稳压强对球膜刚度变化最敏感,对加强筋刚度变化不敏感,并且材料属性的改变主要减小了环向应变,导致凸出角减小,环向余料减小,屈曲压强增大。

3)在球膜幅数不变时,凸出半径越大(或凸出角度越小),鼓包越小,即环向余料越少,临界失稳压强越大。但凸出半径过大将导致球膜承受过大的应力。因此,超压气球设计需要在球膜应力最大化与环向余料最小化之间取得平衡。设计时,可适当增加球膜厚度和鼓包凸出半径来提高球体稳定性。

不足之处在于计算获得的临界屈曲压强较试验值偏低,但在趋势上与试验保持一致。由于对材料属性的资料掌握较少,材料属性的设置与实际值有一定差距,这可能导致计算值与试验有一定的偏差;筋膜之间的共节点约束与实际情况也有不同,这也可能是导致计算值偏低的原因。此外,由于试验数据较少,目前尚不能准确量化几何参数设计与稳定性的关系。今后研究工作的重点是了解材料属性,量化材料属性、几何参数与临界失稳压强的关系。提高临界失稳压强使其高于工作压强对工程实际更有指导意义。