表面缝隙对透波材料RCS的影响分析

2023-07-03于天立董文锋

计算机仿真 2023年5期

于天立,董文锋

(1. 空军预警学院,湖北武汉 430019;2. 空军石家庄飞行学院,河北石家庄 050051)

1 引言

对于新一代飞行器、坦克、舰船、导弹等,利用隐身技术提高其战场生存力是现在乃至未来的发展趋势[1,3]。雷达是探测飞行器目标的主要手段,这就要求了现代飞行器在概念设计阶段就要依据其作战任务的不同、战场环境的差异及受威胁程度的大小,把雷达隐身作为其设计的重要技术指标[4,6]。

随着隐身技术的不断发展,飞行器的雷达隐身性能越来越强。传统飞行器的强散射源,如飞行员驾驶舱、进气道、机翼、雷达舱等都得到了有效的RCS抑制和减缩[7]。但是,受制造工艺、技术条件的限制,飞行器表面会出现诸如缝隙、台阶、铆钉等不连续的特征(即电磁缺陷)[8]。一方面,这些不连续的特征受电磁波照射时,由于其表面不连续的物理特征将引起的目标表面行波、蠕波等的二次辐射;另一方面则是其自身对入射电磁波的直接响应,比如缝隙结构在受电磁波照射时产生的反射、边缘绕射、折射等[9,15]。在这两个方面的作用下,这些不连续特征成为了弱散射源;在强散射源被有效抑制的情况下,弱散射源对目标隐身性能的影响日益突出。因此,对其散射机理进行深入研究就显得尤为重要[16]。由于透波材料良好的透波性能,使其被广泛用于隐身飞行器的设计中,但也正是由于其良好的透波性能,使其表面不连续特征的电磁散射特性相对于传统的金属机身材料发生了改变,从而使其对载体RCS特征的影响发生了变化。本文以缝隙为代表、透波平板为载体,借助电磁计算软件FEKO对不同情况下目标的单站RCS进行仿真。通过改变方形透波平板上缝隙的宽度、深度、数量和极化方式,探究透波材料表面的不连续特征对隐身飞行器RCS的影响及变化规律,与金属材料进行对比并给出结论[17]。

2 单缝隙载体RCS建模与仿真分析

2.1 单缝隙载体建模

研究采用平板型载体模型,上面带有代表电磁缺陷的缝隙。为了抑制电磁波入射时平板载体棱边的边缘绕射,减少透波平板载体自身的电磁散射对缝隙结构散射的影响,故将边长为l、厚度为d、位于YOZ平面上的正方形透波平板的一条对角线放置于Y轴上,设透波材料为非磁性的,μ=μ0,介电常数ε=εr+jεi、损耗角正切tanδ=εi/εr;在透波平板载体上以Z轴为中线做长度为l、宽度为m、深度为n的长方体缝隙,电磁波扫描面位于XOY平面内,入射方位角度φ为电磁波入射方向与X正半轴的夹角,如图1所示。

图1 平板缝隙载体模型示意图

固定透波平板边长度l、平板厚度d、缝隙长度l、透波材料电磁参数(μ,ε),通过设定不同宽度与深度的缝隙,探究不同情况下缝隙对透波平板载体RCS的影响。

2.2 单缝隙对透波载体RCS影响的仿真分析

缝隙属于弱散射源,在弱散射源分析时,微弱的电磁波动可能会造成结果分析时结论的不同,故在进行仿真计算时采用具有较高计算精度的MOM算法(矩量法)。

设透波平板边长度l=1000mm,厚度d=5mm;缝隙长度l=1000mm。在探究缝隙宽度变化对载体RCS的影响时,固定缝隙深度n=4mm,缝隙宽度m分别取10、15、20、25、30mm进行建模;在探究缝隙深度变化对载体RCS的影响时,固定缝隙宽度n=30mm,缝隙深度n分别取0.5、1、2、3、4mm进行建模;透波材料为非磁性材料,磁导率取μ=μ0,介电常数取εr=3.55、电损耗角正切取tanδ=0.003;电磁波入射频率f以0.5GHz、1.5GHz、3GHz三个频点分别代表P、L、S三个波段,入射方位角φ=0°～90°,步长为1°;定义入射电磁波的电场方向平行于波束入射面时为VV极化(垂直极化)、垂直于波束入射面时为HH极化(水平极化),分别对透波材料的载体模型在HH极化与VV极化方式下进行RCS仿真,仿真结果如图2、3、4所示。

图2 不同极化方式下,不同宽度、深度的缝隙对透波平板载体RCS影响的仿真结果(f=0.5GHz)

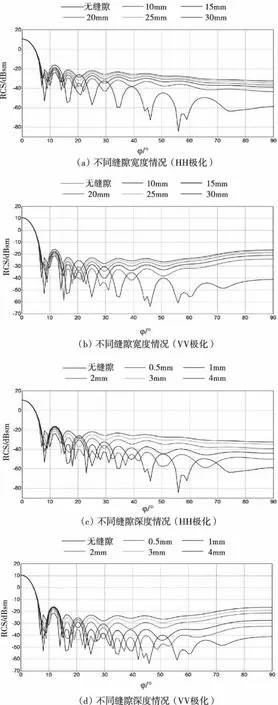
图3 不同极化方式下,不同宽度、深度的缝隙对透波平板载体RCS影响的仿真结果(f=1.5GHz)

图4 不同极化方式下,不同宽度、深度的缝隙对透波平板载体RCS影响的仿真结果(f=3.0GHz)

单缝隙对纯金属平板载体RCS的影响在文献[18]中已经做了充分的分析与论证:①当入射电磁波的电场方向垂直于缝隙走向时缝隙对载体的RCS的增幅明显大于入射电磁波的电场方向平行于缝隙走向时,即入射电磁波极化方式的不同会导致缝隙对纯金属平板载体RCS的影响存在差异;②当入射波入射频率为P波段与L波段时,缝隙对纯金属平板载体RCS的影响微小;③无论入射电磁波是HH极化还是VV极化,缝隙对载体RCS的影响都会随着入射频率、缝隙宽度、缝隙深度的增大而变大,且随着入射频率的提高单位缝隙宽度与深度的变化对纯金属载体RCS的影响变大,但是当缝隙宽度大于1/4波长时,RCS增幅趋于平缓或微弱下降。

从图2、3、4可以看出,与单缝隙对金属平板载体RCS的影响所不同的是:①改变入射电磁波的极化方式,缝隙对于透波平板载体RCS的影响并未发生太大的变化;②当入射波入射频率为P波段与L波段时,缝隙对透波平板载体RCS仍然存在明显的影响;③因缝隙宽度与深度变化而对透波载体RCS产生的影响受频率变化影响不大。

保持入射频率不变时,在缝隙对载体RCS的影响会随着缝隙宽度、缝隙深度的增大而变大,且当缝隙宽度大于1/4波长时,RCS增幅趋于平缓或微弱下降,这一结论上单缝隙对透波平板载体RCS的影响与单缝隙对金属载体RCS的影响保持一致。

3 多缝隙载体RCS建模与仿真分析

无论是机翼还是机身,在隐身飞行器表面上的不连续特征分布规律往往表现为多列、多行平行分布,对于不连续特征在不同入射频率、极化方式、缝隙宽度、缝隙深度的情况下对透波载体RCS的影响已在第1节做了充分的分析,故本节探究固定宽度与深度的多列平行缝隙,在电磁波以3GHz频率HH极化方式入射时对透波载体RCS的影响进行论证与分析。

3.1 多缝隙散射相干原理

RCS是指雷达入射方向上单位立体角内返回散射功率与目标截获的照射功率密度之比[19],所以在讨论多缝隙对载体RCS影响的问题上可以转换为讨论多缝隙对载体散射场强度的影响。将缝隙载体的散射场强度分为3个部分:不存在缝隙的载体、缝隙、存在缝隙的载体,其散射场强度分别为Ez、Eg、Ezg。按照矢量叠加原理有

Ezg=Eg+Ez

(1)

根据矢量叠加原理可知,多列平行缝隙的散射场强度为每一个缝隙散射场强度的矢量叠加和,设多列平行缝隙位于YOZ平面内,ci表示第i个缝隙,缝隙总个数为n;ti表示第i个缝隙与第i+1个缝隙之间的距离;电磁波扫描面位于XOY平面内,垂直于多列缝隙所构成的平面,电磁波入射角度φ为电磁波入射方向与X正半轴的夹角,示意图如图5所示。

图5 多列缝隙示意图

由于每个缝隙间存在距离差,故缝隙与缝隙之间在电磁波入射方向存在相位差,设c1的相位为φ1,c2与c1之间的相位差为△φ1,ci+1与ci之间的相位差为△φi;再设c1缝隙的散射场强度为E1,其对应的c2缝隙的散射场强度为E2,以此类推ci缝隙的散射场强度为Ei,Li表示第i个缝隙在缝隙走向方向上的长度,由相位差可得

(2)

式中,φi-1′表示第i个缝隙与第一个缝隙之间的相位差。设λ表示入射电磁波的波长,φi-1′可以表示为

(3)

根据矢量叠加原理,多列平行缝隙所构成的总散射场强度可表示为

(4)

将式(4)代入式(1)可将缝隙载体的散射场强度表示为

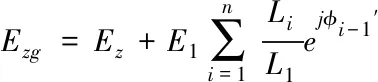
(5)

由于平板载体已经经过旋转处理,减少了平板的边缘绕射对仿真计算结果所带来的影响,故在矢量叠加时Ez与Eg因为方向不同而对结果造成的影响较小,式(5)将探究多个矢量散射源辐射的问题转换为探究一个矢量散射源辐射与散射源之间距离的问题,可适用于研究不同长度与不同间距的多平行缝隙对目标载体RCS的影响。

3.2 多缝隙对透波载体RCS影响的仿真分析与验证

以三列平行缝隙透波载体为例,分别对等间距等长度缝隙载体、等间距不同长度缝隙载体、等长度不同间距缝隙载体进行RCS数值仿真进行验证。

图6所示为带有三列平行缝隙的透波载体示意图,透波平板参数与电磁波入射参数同单缝隙模型,缝隙参数同图5。

图6 三列平行缝隙透波载体示意图

在分析多水平缝隙对目标载体RCS的影响时,由于受到散射源相干原理的影响,每一种组合的散射场强度在矢量叠加时的相位差可能是不同的,所以应先将平行多缝隙组进行组合,分别讨论每一个组合的散射场强度对目标载体RCS的影响。故将c1、c2、c3进行组合,设Ea为c1、c2、c3组合的散射场强度、Eb为c1、c2组合的散射场强度、Ec为c1、c3组合的散射场强度、Ed为c2、c3组合的散射场强度。

3.2.1 等间距等长度三列平行缝隙透波载体RCS仿真分析

载体模型如图6所示,设三列缝隙间距相等且t1=t2=200mm;缝隙宽度m=10mm,c1、c2、c3对应的缝隙长度L1=L2=L3=1000mm;电磁波入射频率为3GHz,波长λ=100mm,入射方位角度为φ。对三列平行缝隙透波载体与不含缝隙的透波载体进行RCS数值仿真,结果如图7所示。

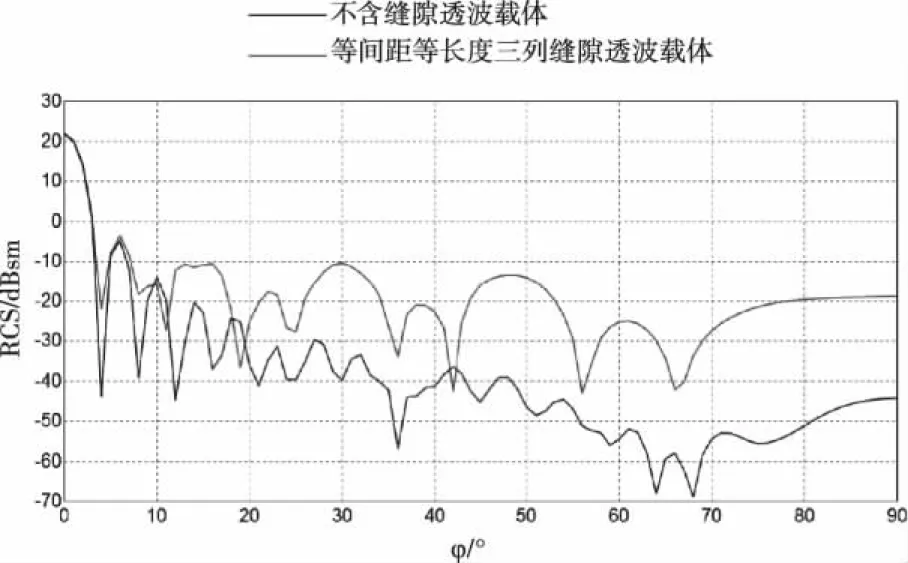
图7 等间距等长度三列缝隙透波载体RCS数值仿真对比图

对于三列等间距等长度平行缝隙而言,根据式(4)可简化得

(6)

式(6)取最大值时,cos△φ1=1,再由式(3)可得

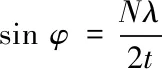
(7)

式中,N为自然数并对应RCS曲线中波峰的位置序号,t为两列缝隙之间的距离。随着电磁波入射角度的变化,对应的RCS曲线取波峰值时,即经矢量叠加散射场强度Ea取最大值时,sinφ分别取0、0.25、0.5、0.75、1,对应入射方位角φ分别取0°、14.5°、30°、48.6°、90°;同理可得,由于相位差相同的原因,经矢量叠加散射场强度Eb、Ed取最大值时入射方位角φ的取值与Ea时的相同;同理可得,经矢量叠加散射场强度Ec取最大值时,sinφ分别取0、0.125、0.25、0.375、0.5、0.625、0.75、0.875、1,对应入射方位角φ分别取0°、7.2°、14.5°、22°、30°、38.7°48.6°、61°、90°。

将理论分析与图7的仿真结果进行对比,可以发现:①当入射方位角φ为0°与7.2°时,目标载体发生镜面反射,此时,缝隙散射场淹没于镜面反射中,入射方位角10°以内的3个波峰都是由于目标载体的镜面反射所引起的;②当入射方位角φ为14.5°、30°、48.6°时,RCS数值曲线出现明显波峰,此时波峰的出现是三列缝隙散射场的耦合效应所引起的,与其它波峰相比,这些角度的波峰具有幅值较高,覆盖角度范围较广的特点;③当入射方位角φ为22°、38.7°、61°时RCS数值曲线出现明显波峰,此时波峰的出现是c1、c3两列缝隙散射场的耦合效应所引起的;④当入射方位角φ接近90°时,由于电磁波入射方向与透波载体平面所构成的角度较小,载体棱边的边缘、尖顶绕射效应已不可忽略并构成了新的散射源,此时出现一个覆盖角度范围极广的波峰,此时波峰出现的原因是三列平行缝隙与载体棱边、尖角共同的耦合效应所引起的。

3.2.2 等间距不同长度三列平行缝隙透波载体RCS仿真分析

载体模型如图6所示,设三列缝隙间距相等且t1=t2=200mm;缝隙宽度m=10mm,缝隙长度L1=700mm、L2=1000mm、L3=500mm;电磁波入射频率为3GHz,波长λ=100mm,入射方位角度为φ。对三列平行缝隙透波载体进行RCS数值仿真,结果如图8所示。

图8 等间距不等长度三列缝隙透波载体RCS数值仿真对比图

将已设参数代入式(4)可得

Ea=E1ejφ1(1+ae-jΔφ1+bejΔφ1)

(8)

式中,a=L3/L2=0.5、b=L1/L2=0.7,但是由于式(8)中参数a、b的取值对于Ea取最大值时△φ1的取值没有影响,影响的只是Ea的最值大小,所以等间距不同长度的三列缝隙与等间距同长度的三列缝隙对于目标载体在RCS波峰位置的影响上是相同的,在这种情况下不同的只有RCS峰值的幅度。

图8是等间距不同长度的三列缝隙与等间距同长度的三列缝隙对于目标载体在RCS影响的对比图,可以发现两条RCS曲线出现的角度是一样的,但是由于c1、c3两列缝隙的长度都有减少,c2缝隙的长度并未减少的原因,Ea受影响的程度小于Ec受影响的程度,从图8中可以发现,因c1、c2、c3三列缝隙射场耦合效应所引起的波峰处的RCS差值小于因c1、c3两列缝隙射场耦合效应所引起的波峰处的RCS差值,进一步证明了理论的正确性。

3.2.3 不同间距等长度三列平行缝隙透波载体RCS仿真分析

载体模型如图6所示,设三列缝隙间距相等且t1=200mm、t2=150mm;缝隙宽度m=10mm,缝隙长度L1=L2=L3=1000mm;电磁波入射频率为3GHz,波长λ=100mm,入射方位角度为φ。对三列平行缝隙透波载体与仅有c1、c3两列平行缝隙透波载体进行RCS数值仿真,结果如图9所示。

图9 不等间距等长度三列缝隙透波载体RCS数值仿真对比图

将已设参数代入式(4)可得

Ea=E1ejφ1(1+e-jpΔφ1+ejqΔφ1)

(9)

式中,p=1、q=t1/t2=4/3。经由式(3)、式(8)计算,同理可得,经矢量叠加散射场强度Ea取最大值时,sinφ分别取0、1,对应入射方位角φ分别取0°、90°;经矢量叠加散射场强度Eb取最大值时,sinφ分别取0、0.25、0.5、0.75、1,对应入射方位角φ分别取0°、14.5°、30°、48.6°、90°;经矢量叠加散射场强度Ec取最大值时,sinφ分别取0、1/3、2/3、1,对应入射方位角φ分别取0°、14.5°、30°、48.6°、90°;经矢量叠加散射场强度Ed取最大值时,sinφ分别取0、1/7、2/7、3/7、4/7、5/7、6/7、1,对应入射方位角φ分别取8.25°、16.6°、25.4°、34.8°、45.6°、59.5°、90°。

将理论分析与图9的仿真结果进行对比验证,可以发现:①经矢量叠加散射场强度Eb、Ec应出现RCS波峰的角度与经矢量叠加散射场强度Ed出现波谷的角度相临近,所以在这些角度上载体的RCS曲线并未出现RCS波峰;②三列平行缝隙载体出现RCS波峰的角度与仅有c1、c3两列平行缝隙透波载体出现RCS波峰的角度与幅值都基本相同,进一步说明了此情况下透波载体的RCS主要受矢量叠加散射场强度Ec所影响。