舰载光电设备视轴稳定技术研究
2023-07-03杨维帆李德全
谢 航,杨维帆,李德全,王 栋
(1. 中国科学院长春光学精密机械与物理研究所,吉林 长春 130033;2. 中国科学院大学,北京 100049)
1 引言
近年来,雷达和光电跟踪器的配合日益密切,尤其在水域感知技术中[1]。雷达系统具有探测主动性,探索范围足够大,抗干扰能力强,不受天气及能见度影响。但缺点是无法对目标成像,目标的识别困难,细节分辨率能力不够[2]。光电系统作为一种光电探测设备,具有能成像、细节分辨率能力强的优势[3];光电系统属于无源探测设备,本身不辐射能量,通过接收目标辐射热能进行目标探测和定位,因而具有很大的隐蔽性,不易被侦察和定位,具有较强的抗有源电子干扰能力[4]。但缺点是受气象条件约束,易受海杂波干扰,无法全天侯工作[5]。两者组合成的探测系统能发挥各自优点,互为补足。光电跟踪系统利用雷达系统的引导信息实现对目标的搜索、定位及跟踪[6]。舰载光电设备受船摇扰动(横摇、纵摇、艏摇)的影响,使视轴晃动,造成图像模糊,甚至丢失目标[7]。为快速并准确搜索、定位及跟踪目标,减小光电设备在跟踪瞄准时船摇带来的扰动误差,需选择合适的视轴稳定策略。
目前实现视轴稳定的方法从原理上讲有两种:一种是构建机械稳定平台,通过反方向的运动来克服舰船的摇摆, 该方法结构复杂, 精度低[8,9]。另外一种就是利用伺服稳定控制技术将设备直接安装在甲板上,通过敏感元件获取舰船运动的信息,将目标运动和载体运动进行综合解算,借助旋转矩阵把由载体运动导致的方位角和俯仰角的变化经坐标变换来修正视轴的指向[10]。该方法结构简单且提高了视轴的控制精度。
第二种方法-基于旋转矩阵的轴角补偿算法适用于已知目标在地理坐标系下的方位及俯仰信息的船摇扰动补偿[11]。当舰载光电设备工作在特殊工况下,例如方位轴摆扫、俯仰轴定位即已知目标在甲板系下的方位信息和地理系下的俯仰信息时,该补偿算法不再适用。
针对特殊工况下的视轴稳定问题,本文改进了基于旋转矩阵的轴角补偿算法:通过参考坐标系的变换,首先推导出舰载光电设备的方位轴摆扫、俯仰轴定位这一特殊工况下视轴稳定的关系式,其次建立了光电设备在不同的工况下跟踪动目标时视轴稳定的数学模型。最后在MATLAB/simulink上进行仿真。改进的补偿算法可解决舰载光电设备在特殊工况下视轴稳定的问题。
2 坐标系定义及坐标系变换
为了对船摇扰动进行补偿或校正,首先定义几种坐标系,根据地理坐标系与甲板坐标系之间的变换关系,建立起地理坐标系下的方位角AD、俯仰角ED与甲板坐标系下的方位角AC、俯仰角EC之间转换的数学模型[12]。
2.1 坐标系及船摇参量定义
地理坐标系:
地理坐标系为O_XDYDZD。以惯导中心为原点O,O_YD轴指向正北,O_XD轴指向正东,O_ZD轴指向天顶成右手系。
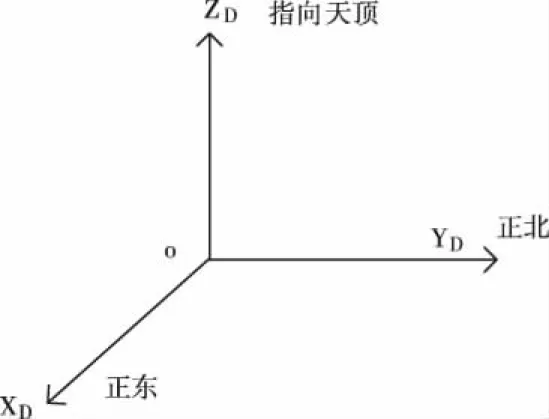
图1 地理坐标系
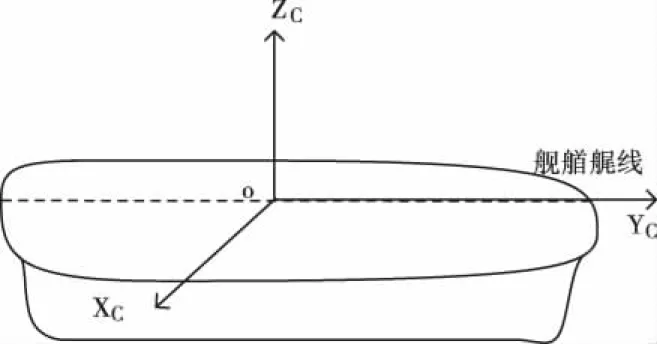
图2 甲板坐标系

图3 设备坐标系

图4 船摇参数定义图示

图5 地理坐标系中目标位置
甲板坐标系:
甲板坐标系为O_XCYCZC。以惯导中心为原点O,O_YC轴指向舰船的艏艉线,舰艏为正;O_ZC轴垂直甲板面,向上为正;O_XC轴与O_ZC轴及O_YC轴成右手系。
方位框架坐标系:
方位框架坐标系为O_XaYaZa。以光学设备中心为原点O,O_Za轴与O_ZC轴重合,垂直于甲板面向上为正;O_Xa轴与俯仰轴重合,设备右侧方向为正;O_Ya轴与O_Za轴及O_Xa成右手系。
俯仰框架坐标系:
俯仰框架坐标系为O_XrYrZr。以光学设备中心为原点O,O_Yr轴指向光电设备的视轴,视轴朝前为正;O_Xr轴与俯仰轴重合,设备右侧方向为正;O_Zr轴与O_Yr轴及O_Xr成右手系。
船摇参数定义如下图:
横倾角R是舰体绕艏艉线相对水平面的转角,右舷下降为正;纵倾角P是舰艏艉线相对水平面的转角,舰艏抬高为正;艏向角H是舰艏艉线在水平面的投影与正北的夹角,顺时针方向为正。
2.2 地理坐标系与甲板坐标系的转换
将目标的地理极坐标位置(设目标信息为:距离舰艇D、地理方位角AD、地理俯仰角ED[12])变换为地理系下直角坐标。
Xd=D*cos(ED)*sin(AD)
Yd=D*cos(ED)*cos(AD)
Zd=D*sin(ED)
(1)
地理系直角坐标到甲板系直角坐标的转换:
采用先艏摇再纵摇后横摇的旋转次序建立3个子变换矩阵,即分别只转过H、P、R角度,得到相应的艏向变换阵TH、纵倾变换阵TP、横倾变换矩阵TR,再用矩阵乘积运算综合3个船摇状态[13]:
(XC,YC,ZC)T=TRTPTH(XD,YD,ZD)T
展开得到船摇位置矩阵变换公式
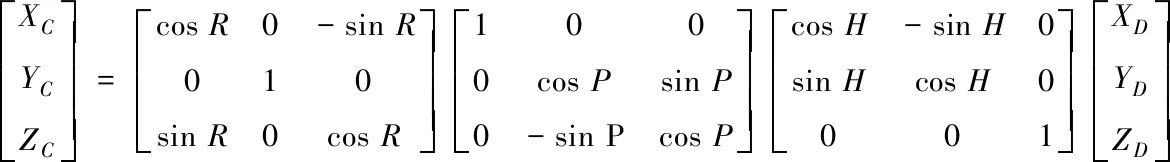
(2)
计算目标在甲板系下的方位角和俯仰角
AC=tan-1(XC/YC)
EC=sin-1(ZC/D)
将式(1)、(2)带入上式可得到坐标变换公式

(3)
EC=sin-1{cos(ED)[sin(R)sin(AD-H)-cos(R)sin(P)cos(AD-H)]+sin(ED)cos(R)cos(P)}
(4)
同理可得坐标反变换公式

(5)
ED=sin-1(cos(EC)(sin(P)cos(AC)-cos(P)sin(R)sin(AC))+cos(R)cos(P)sin(EC))
(6)
3 视轴稳定算法原理
3.1 摆扫视轴稳定数学模型推导
光电跟踪器在摆扫时可等效为跟踪甲板系下方位角度为AO(t)、地理系下俯仰角度为ED的动目标。该目标在甲板系下的方位速度变化如图6所示。
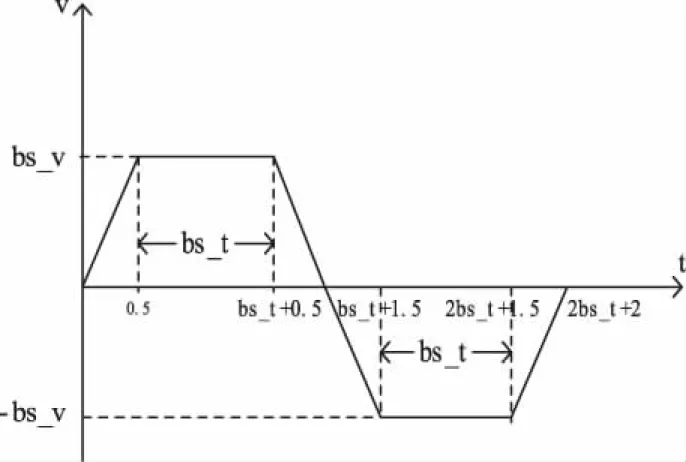
图6 摆扫时方位轴运动速度曲线

图7 摆扫视轴稳定仿真图
根据上图速度曲线,可确定方位速度回路的输入量,保证方位轴在甲板系下完成摆扫运动。船摇的影响会导致俯仰轴角位置在地理系下发生变化,为保证俯仰角度为常值,所以对船摇扰动对俯仰轴的影响进行实时补偿。
初始时刻方位框架坐标系运动,俯仰框架坐标系与其固连,此时甲板系下方位框架角度为AO(t),俯仰角EO=0°。为保证俯仰角度在地理系下为常值,需将目标在地理系下的俯仰角和方位角带入式(4)中,可求出俯仰轴在甲板系下的角度控制量。俯仰角度为已知常值,由于方位角度未知,需要对它进行求解。
已知目标在甲板系下方位角度及俯仰角度求其在地理系下方位角度,可通过式(5)求出。将AO(t)、EO=0°带入得到
AD(t)=
将AD(t)及ED带入角位置变换式(3)及(4)中解算出AC(t)及EC(t)。
EC(t)=sin-1{cos(ED)[sin(R)sin(AD(t)-H)-cos(R)sin(P)cos(AD(t)-H)]+sin(ED)cos(R)cos(P)}
EC(t)为俯仰伺服系统控制量。以EC(t)为俯仰伺服系统输入量,即可保证俯仰角度在地理系下为常值。
3.2 动目标数引跟踪视轴稳定算法原理
已知目标不同位置引导信息,光电跟踪设备进行数引跟踪时,可分为以下4种情况来考虑:
1)已知目标在地理系下的坐标为(AD(t),ED(t))。
直接按正变换求解出AC(t)、EC(t)。将AD(t)及ED(t)带入(3)、(4)式中得
EC(t)=sin-1{cos(E(t))[sin(R)sin(A(t)-H)-cos(R)sin(P)cos(A(t)-H)]+sin(E(t))cos(R)cos(P)}
将AC(t)、EC(t)作为方位与俯仰位置回路输入量。
2)已知目标在甲板系下的位置信息为(AC(t),EC(t))时,直接将AC(t)、EC(t)作为方位与俯仰位置回路输入量。
3)已知目标在地理系下的俯仰信息为ED(t),甲板系下的方位信息为AC(t)。
由于方位轴摆扫模式是该类的一个特例,该类分析过程与摆扫模式的分析过程一致,这里就不再赘述。将AC(t)及EC=0°带入反变换式(5)中得
将AD(t)及ED(t)带入正变换式(3)(4)中得
EC(t)=sin-1{cos(ED(t))[sin(R)sin(AD(t)-H)-cos(R)sin(P)cos(AD(t)-H)]+sin(ED(t))cos(R)cos(P)}
4)已知目标在甲板系下的俯仰信息为EC(t),地理系下的方位信息为AD(t)。
将AD(t)及ED=0°带入正变换式(3)中得
将AC(t)、EC(t)作为方位与俯仰位置回路输入量。动目标的数引信息按以上类别划分后,采用相应的视轴稳定策略,光电系统可实现对动目标的稳定跟踪。
4 仿真研究
4.1 摆扫视轴稳定算法仿真验证
在MATLAB/simulink中搭建模型,对摆扫视轴稳定算法进行仿真验证,该模型简化处理,省略了控制器及被控对象模型。仿真模型共包括惯导模拟发生模块、方位位置发生模块、地理坐标系到甲板坐标系正变换模块以及甲板坐标系到地理坐标系反变换模块。船摇参数及给定量如表1所示。

表1 船摇及给定量参数表
仿真结果如下所示。
图8至图11表明,舰船摇摆对俯仰位置的干扰作用是非常明显的。在船摇作用下,地理系下俯仰角的数据特性发生了明显地变化,本应平滑的曲线变得带有类似船摇数据的周期性起伏,在观测时间内幅值在20°左右波动,其幅值波动与方位轴摆扫周期及摆扫速度相关。采用稳定策略后,将EC(t)作为俯仰伺服系统输入量能补偿船摇扰动对光电跟踪系统的影响。由于以上仿真是在理想情况下,忽略了惯导数据误差以及光电设备编码器的测量误差,实际工程中不能做到对船摇位置干扰的全补偿。在原有仿真模型基础上,再搭建一组系统并引入误差,比较引入前后EC(t)的变化。工程中可认为船体姿态与仪器方位及俯仰角的测量误差为高斯噪声[13],所以在新系统中加入均值为0,方差为0.04的高斯噪声。

图8 摆扫周期10s、摆扫速度20°/s给定及稳定效果曲线图
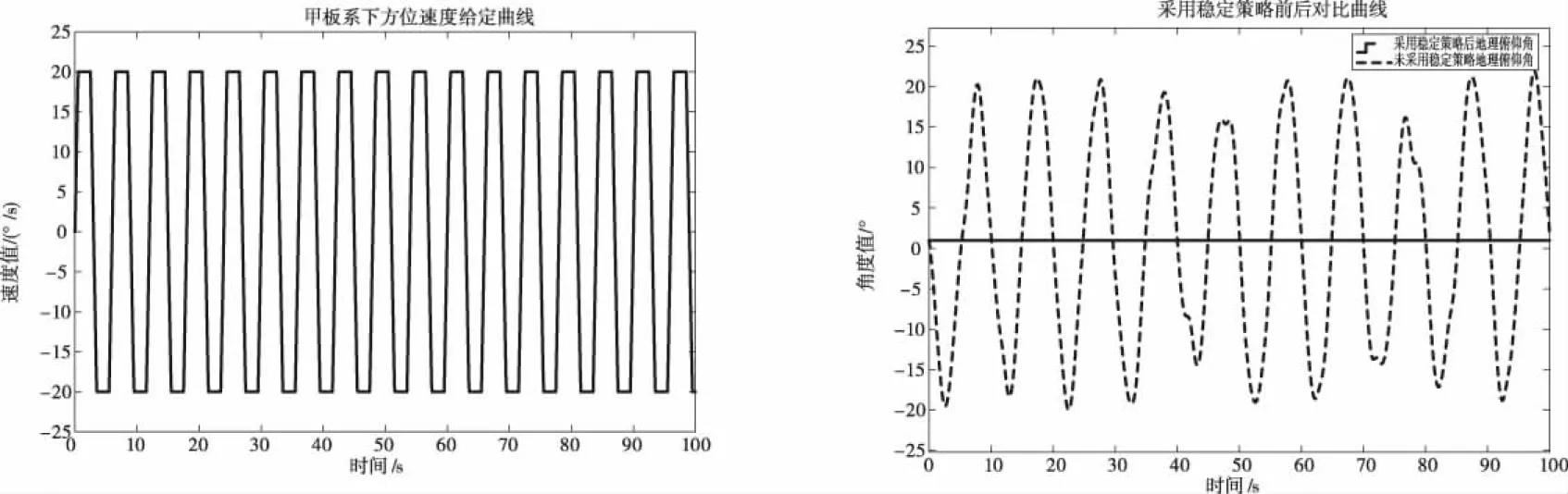
图9 摆扫周期6s、摆扫速度20°/s给定及稳定效果曲线图

图10 摆扫周期10s、摆扫速度10°/s给定及稳定效果曲线图

图12 摆扫视轴稳定系统引入噪声对比仿真图
仿真结果如下图所示。
从图13至图15可以看出,俯仰解算量曲线呈类似正弦周期性变化,引入噪声前后解算的俯仰角度误差在俯仰解算量曲线的波峰和波谷处最大、在过零点处最小。原本引入的高斯噪声,传递到俯仰角时,已经不再是高斯噪声,与船体姿态和仪器方位与俯仰位置有着严重的耦合。从图15与图16中可以看出,对应噪声方差0.04的误差曲线在-1°与1°之间波动,对应噪声方差0.09的误差曲线在-1.5°与1.5°之间波动。表明俯仰角度误差的波动幅度与引入的高斯噪声方差大小有关,即船体姿态与仪器方位及俯仰角的测量误差影响伺服系统控制器的输入,这为惯导及编码器的选型提供参考依据。
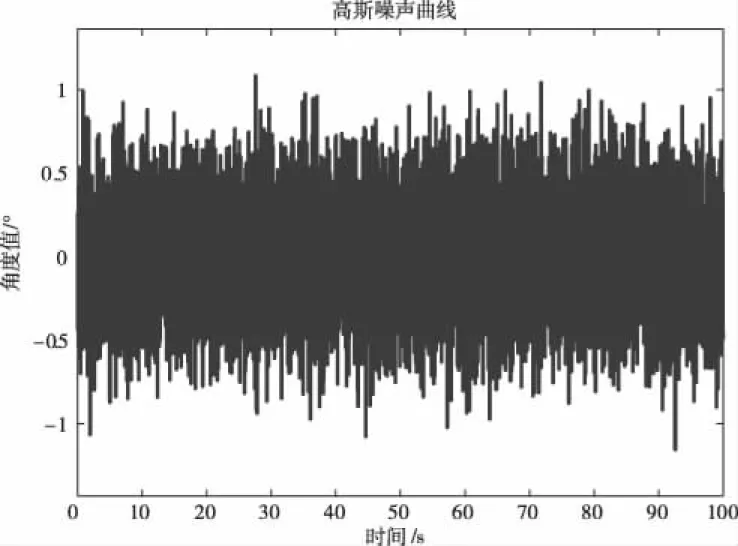
图13 引入噪声曲线

图14 引入噪声前后俯仰解算量对比曲线

图15 噪声方差为0.04的俯仰角度误差曲线

图16 噪声方差为0.09的俯仰角度误差曲线

图17 动目标跟踪视轴稳定仿真图
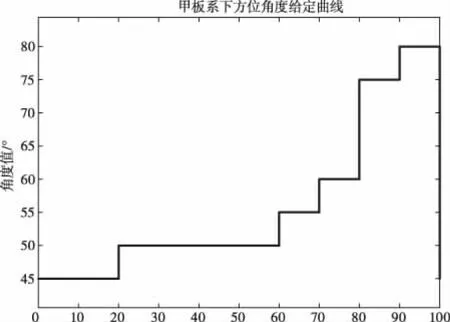
图18 目标在甲板系下的方位位置曲线

图19 目标在地理系下的俯仰位置曲线
4.2 动目标数引跟踪仿真验证
以第三类数引信息即已知目标在地理系下的俯仰信息为ED(t),甲板系下的方位信息为AC(t)为例进行仿真验证。利用MATLAB/simulink搭建模型,该模型简化处理,省略了控制器及被控对象模型。船摇参数与表一一致。
仿真结果如下所示:
图20表明,在船摇作用下,目标在地理系下的俯仰角发生了明显地变化,在观测时间内摆动幅值约为21.06°。采用稳定策略后,将EC(t)作为俯仰伺服系统输入量能补偿船摇扰动对光电跟踪系统的影响。

图20 采用稳定策略与未采用稳定策略效果对比图
5 总结
本文针对舰载光电跟踪设备在特殊工况下的视轴不稳定问题,改进了基于旋转矩阵的轴角补偿算法。经过仿真得出以下结论。
1)针对舰载光电设备方位轴摆扫、俯仰轴定位这一特殊工况,所改进的算法是有效的。在五级海况下,补偿前光电设备在地理系下俯仰角的幅值在20°左右周期性波动,经改进算法补偿后光电设备俯仰角稳定在地理系下给定值1°。
2)经改进算法解算后的俯仰角度控制量的数据特性与方位轴摆扫周期、摆扫速度以及传感器测量噪声相关。引入噪声前后,解算的俯仰角度误差曲线波动的幅值与高斯噪声的方差相关,为惯导及编码器的选型提供了参考依据。
3)针对舰载光电设备在目标数引信息引导下跟踪动目标问题,将数引信息分为4类,以第三类即已知目标在地理系下的俯仰信息,甲板系下的方位信息为例,证明了改进算法的通用性。在五级海况下,补偿前光电设备在地理系下俯仰角的幅值波动约为21.06°,经改进算法补偿后光电设备俯仰角稳定在地理系下给定曲线。
