角度误差下管路连接结构装配及其对密封的影响*
2023-07-02杜双言瞿品祥黄晓鸣
杜双言 张 伟 瞿品祥 黄晓鸣
(1. 大连理工大学机械工程学院 辽宁大连 116024; 2. 中国航发南方公司 湖南株洲 412000)
管路连接结构作为航空航天液压系统的重要组成部分, 分布范围广, 工作环境复杂, 其中装配偏差是造成管路连接结构失效的重要原因。 现阶段由装配不当产生的初始装配应力对管路连接结构及其对管路系统密封性的削弱还没有被重视起来, 针对管路连接结构, 进一步了解和研究装配偏差下管路连接结构密封性能的变化规律和密封机制具有重要意义。
近年来针对管路连接结构的密封性能, 学者们展开了大量的研究。 在管路连接结构密封性能方面, 欧阳小平等[1]详细介绍了不同种类管路连接结构的特点; 李枫等人[2]介绍了不同管接头密封失效的概率。税晓菊等[3]研究了24°管路堵头与管接头的性能差异, 以及堵头密封性能在不同因素下的变化规律。YAN 等[4]建立了真实表面下的管接头密封区域模型,揭示了紧固过程中管路连接结构密封形成过程及对密封特性的影响规律。 崔颖等人[5]设计了一种梁式管接头, 通过有限元分析和试验相结合得到了管接头结构参数对密封性能影响的敏感性。 杨卓然等[6]建立有限元模型结合实验研究了影响锥面密封性能的主要因素。 翟富刚等[7]介绍了新型超高压管接头的结构形式, 基于有限元分析研究了不同结构参数对管接头密封性能的影响。 冉光斌和张方晓[8]分析了影响双锥面密封结构密封性能的主要因素, 找到了合理的双锥形管路连接结构参数并进行了验证。
针对装配参数带给管路连接结构影响的研究, 主要集中在管接头的拧紧力矩、 管路连接结构的装配偏差等因素。 丁建春等[9]利用有限元分析软件研究了拧紧力矩对管接头密封带宽度的影响, 并进行了试验验证。 熊影辉等[10]建立了扩口式管接头拧紧扭拉关系的理论公式和有限元仿真模型, 验证了扭拉关系理论公式计算结果的有效性。 郑世伟等[11]以无扩口液压管接头为研究对象分析了安装力矩对导管应力应变和密封效果的影响, 并进行了相关试验验证。 王振兴等[12]从机制上分析拉伸载荷下管路连接的密封效果,定量地研究了拉伸载荷对密封要素的影响。
在装配偏差的研究方面, 张旭等人[13]基于Workbench 研究了3 种装配偏差对扩口式管接头密封性能的影响, 并建立了管路密封试验系统进行验证。 周鑫等人[14]研究了球头-锥面结构不对中装配误差对连接结构密封性能的影响, 提出了对管路连接件装配对中偏差要求和拧紧力矩。 夏芝玮等[15]分析了多因素对管路连接件密封性能的影响, 建立了有限元模型, 发现轴向偏差对密封性能影响较大, 径向偏差和角度偏差影响较小。 目前关于装配误差对密封性能的影响方面的研究较少, 大都采用预紧力单元法或强制位移法模拟螺纹提供的预紧力, 无法全面地体现管路拧紧过程中的变形关系。 本文作者建立了保留螺纹的双球头管路连接结构有限元模型, 推导了管接头拧紧过程的扭拉关系公式并与仿真模型相互比较, 研究了存在安装角度偏差下管路连接结构的变形过程及其对密封性能的影响。
1 复合管路连接结构
1.1 管路连接结构密封形成过程
如图1 所示, 双球面管路连接结构主要是由焊接接管嘴、 拧紧螺母、 球形管路三部分组成。 在实际装配过程中, 对拧紧螺母施加扭矩, 通过螺纹连接结构施加轴向预紧力, 在两个球面与接管嘴内锥面产生接触应力, 形成两道密封环, 对管道内的流体进行密封。相对于单球形管路连接结构, 双球形复合管路连接结构形成两道密封环, 密封环之间形成充满空气的封闭空间。 管路在实际使用过程中, 小球面密封带失效时,由于阶梯槽封闭空间内存在空气, 高压液体压力降低,从而减少了大球面密封带内外的压力差, 密封带失效的概率降低, 从而提高了管路连接结构的密封可靠性。

图1 双球头管路连接结构Fig.1 Double-ball pipe connection structure
1.2 管路连接结构扭拉关系
在装配过程中, 管路连接结构一般采用扭矩法进行拧紧, 衡量管路连接结构拧紧质量最重要的指标是管路的密封性, 密封性与管路螺纹结构产生的预紧力有直接关系, 所以研究管路拧紧力矩和其轴向预紧力之间的关系至关重要。 参考螺栓节点扭拉关系公式[16], 对螺母进行受力分析, 螺母受到输入扭矩Ti、螺纹摩擦扭矩Ts、 端面摩擦扭矩Tw, 后两者与前者相互平衡。 螺纹摩擦扭矩Ts可参考螺栓摩擦扭矩公式, 端面摩擦扭矩Tw为端面摩擦力与阻力力臂的乘积, 公式如下。
式中:μs为螺纹摩擦因数;F为管路连接结构预紧力;β为螺纹升角;α为牙型半角;d2为螺纹中径;P为螺纹螺距;μw为端面摩擦因数;dw为端面等效摩擦直径;do为球形接头端面外径,dh为拧紧螺母孔径。
将公式代入求解得到管路连接结构的预紧力与扭矩关系公式为
对于规格为DN4, M14×1.5 mm 的管路连接结构,各参数取值如表1 所示, 代入公式(5) 计算可得
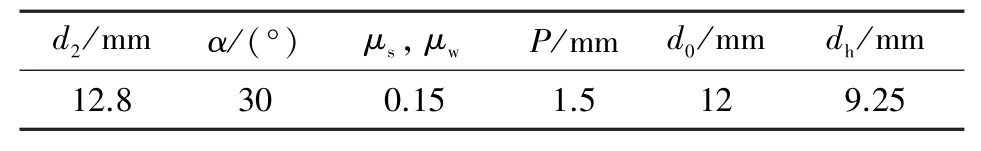
表1 管路连接结构参数Table 1 The parameters of the pipe connection structure
2 复合管路连接结构有限元分析
2.1 参数化有限元模型的建立
为了能进一步地观察双球头管路连接结构的拧紧过程和其密封面应力分布情况, 基于Workbench 建立管径为4 mm、 壁厚为1.5 mm 的24°双球头管路连接结构弹塑性有限元模型, 如图2 所示。

图2 复合管路连接结构有限元模型Fig.2 Finite element model of composite pipeline connection structure
有限元模型中, 焊接接管嘴材料为1Cr17Ni2,拧紧螺母和双球头管路材料为GH1131, 材料参数如表2 所示。 为了保证有限元仿真对工况模拟的真实性, 建立了真实螺纹接触的管路连接结构模型。 模型的初始接触状态如图2 所示有3 个接触对, 拧紧螺母和接管嘴螺纹面接触对、 拧紧螺母端面和球形管接头端面接触对、 球形管接头球面和焊接接管嘴内锥面线接触对。 3 个接触对均为摩擦接触, 摩擦因数设置为0.15。 为减少计算量, 接触行为设置非对称接触, 接触算法采用增广拉格朗日接触算法, 接触探测采用基于高斯积分点的探测。 在有限元网格划分方面, 双球头管路连接结构是通过螺纹结构产生预紧力, 达到密封的效果, 因为螺纹升角的存在, 全部划分为六面体网格难度较大, 所以采用过渡层策略进行网格划分,如图2 所示。 整体采用solid186 高阶六面体单元, 每个单元包括20 个节点, 并有少量的五面体单元位于过渡层位置。 为了保证计算的准确性, 对球头与焊接接管嘴接触部分进行网格加密, 模型总单元数为70 705, 节点数为328 711。 根据双球头管路连接结构实际工况, 边界条件如图2 所示, 在焊接接管嘴左端面处施加Fixed Support, 在球头导管外柱面施加Cylindrical Support, 限制柱面的径向和切向的位移,另外对拧紧螺母外圆柱面施加扭矩载荷。
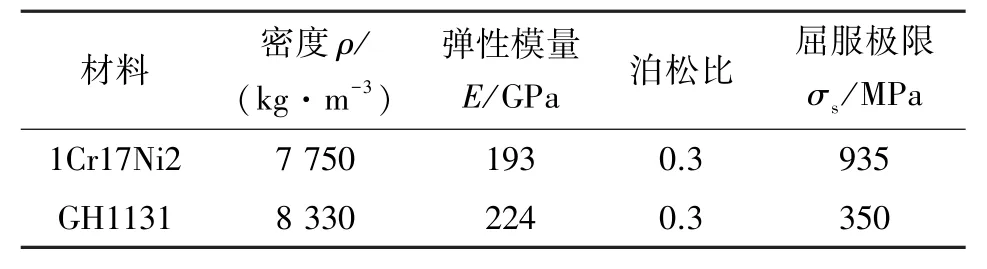
表2 材料参数Table 2 The parameters of material
2.2 管路连接结构扭拉关系的验证
建立输入扭矩仿真组, 变量为输入扭矩T, 取值为5~40 N·m, 间隔为5 N·m, 导出仿真结果与理论公式计算结果对比如图3 所示。 可以看出仿真模型计算结果与理论公式计算值趋势相同, 相对误差在5%以下, 验证了文中建立的有限元模型的有效性。
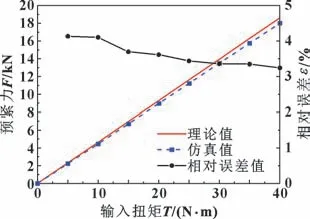
图3 不同输入扭矩下预紧力理论值与仿真值对比Fig.3 Comparison of moment-preload relationship between theory and simulation
3 安装角度偏差下管路连接结构密封性能分析
管路连接结构角度装配偏差是指在装配过程中,双球形导管轴线与焊接接管嘴轴线不平行, 存在一定的夹角, 称之为管路连接结构安装的角度偏差。 其中球形管路球面和接管嘴内锥面由线接触变为点接触,螺母端面与球形管路端面由面接触变为点接触。 建立参数化仿真组, 变量为角度偏差值θ, 取值为0°~1°,间隔为0.1°, 输入扭矩设置为0 ~30 N·m, 其余参数设置为常量, 保持不变。
3.1 安装角度偏差对拧紧过程的影响
以角度偏差θ=0.4°的模型为例, 对照理想状态下管路拧紧过程, 讨论角度偏差对管路连接结构装配的影响。 当管路连接结构存在角度偏差时, 如图4 所示, 初始状态螺母端面与球形管路端面为点接触, 随着拧紧力矩的增大两端面接触面积不断增大, 直至完全贴合; 类似的情况也发生在球头与接管嘴锥面位置, 接触出现非线性现象。 图5 所示为0.4°角度偏差下输入扭矩与预紧力的关系, 可以很明显地看出拧紧过程可以分为两个阶段。 第一阶段为贴合阶段, 在拧紧过程中, 螺母端面缓慢偏转并逐渐克服螺母端面与球头端面的缝隙, 球头管路发生弯曲直至两端面完全贴合, 在此阶段输入扭矩和管路预紧力为非线性关系; 第二阶段端面贴合后, 扭矩与预紧力为线性关系。
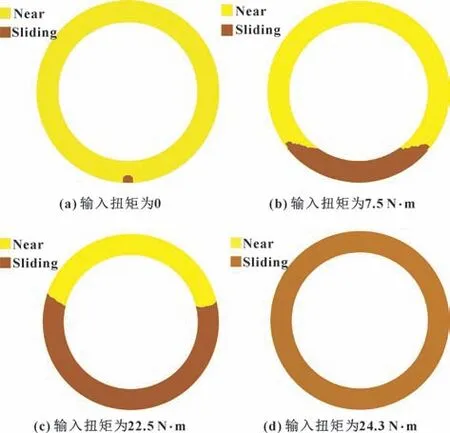
图4 不同输入扭矩下螺母端面与球头管路端面接触状态Fig.4 Contact status on the end face of nut and pipe under different input moments: (a) input moment is 0;(b) input moment is 7.5 N·m; (c) input moment is 22.5 N·m; (d) input moment is 24.3 N·m
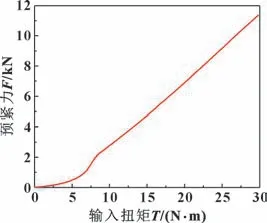
图5 0.4°角度偏差下输入扭矩与预紧力关系Fig.5 Relationship between input moment and preload under 0.4°angle error
导出角度偏差仿真组的预紧力数据, 绘制角度偏差与预紧力关系图, 如图6 所示。 可以看到, 随着角度偏差的增大, 管路连接结构的预紧力减小, 输入扭矩更多地消耗在拧紧的贴合阶段, 最终转化的预紧力变少。
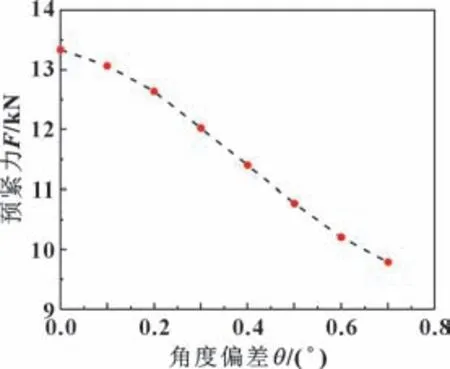
图6 角度偏差与管路预紧力关系Fig.6 Relationship between angle error and preload
3.2 角度偏差对密封性能的影响
为了研究角度偏差下管路连接结构密封性能的变化情况, 对角度偏差0.1°~0.9°情况下密封面部分接触应力进行了分析, 结果如图7 所示。 可以看出, 密封面上应力分布出现明显的不均匀。 将密封面上达到屈服强度350 MPa 的区域视为达到密封要求, 为了能体现管路连接机构整体的密封性能, 定义球面上密封区域最窄的宽度值为球面的密封环宽度。 从图7 中还可以看到, 当角度偏差较小时, 大小球头上的密封带仍近似为宽度均匀的密封环; 但随着角度偏差的增大, 密封环宽度出现明显的不均匀分布, 其中大球头密封环宽度变化较大, 在角度偏差为0.9°时已经无法形成密封环。

图7 角度偏差下密封面接触应力云图Fig.7 Contact stress of sealing surface under angle error:(a) 0.1°; (b) 0.5°; (c) 0.8°; (d) 0.9°
导出密封环部位对应节点的接触应力与密封环坐标, 计算后绘制出角度偏差与密封环宽度的关系图,如图8 所示。 可以看到, 随着角度偏差的增大, 2 个球头上密封环的宽度都不断减小而且密封环宽度减小的速率越来越大, 其中小球头密封环宽度减小速率小于大球头; 当角度偏差达到0.9°时大球头密封环宽度为0.067 mm, 已经无法形成有效密封。
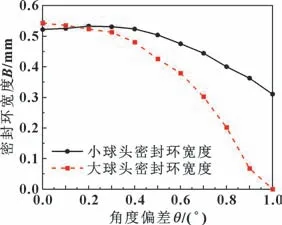
图8 角度偏差与密封环宽度关系Fig.8 Relationship between angle error and the width of sealing ring
4 结论
(1) 存在角度偏差时, 复合管路连接结构拧紧过程分为2 个阶段, 拧紧初期非线性的贴合阶段和线性拧紧阶段。
(2) 复合管路连接结构密封环宽度随角度偏差的增大不断减小直至消失, 其中大球头密封环宽度减少速率大于小球头。
(3) 相同输入扭矩下, 复合管路连接结构预紧力随角度偏差的增大不断减小。
