山地城市地铁平纵曲线交叠区段钢轨波磨打磨限值研究*

崔晓璐 吕 东 包鹏羽 李 童 漆 伟

（1. 重庆交通大学机电与车辆工程学院 重庆 400074； 2. 重庆市轨道交通（集团） 有限公司 重庆 401120）

重庆作为典型的山地城市， 其地铁线路具有坡道多、 曲线半径小等特点， 并存在十分严重的钢轨波磨问题［1-2］。 对重庆地铁十号线进行现场调研， 发现在竖曲线和平曲线交叠区段的低轨上， 有较为普遍的异常波磨现象， 其波长范围为30 ～70 mm， 波深范围为0.02～0.20 mm； 尤其是波长为50 mm 的钢轨波磨出现频繁， 是该区段的一种典型钢轨波磨， 如图1所示。

图1 山地城市地铁平纵曲线交叠区段钢轨波磨Fig.1 Rail corrugation in overlapping section of horizontalvertical curve in mountain city metro

目前普遍认为钢轨打磨是治理钢轨波磨最常用、最直接、 最经济的方法［3］， 而确定钢轨波磨的打磨限值是制定打磨策略和实施打磨计划的关键步骤， 国内外学者对此进行了相关研究。 张晴等人［4］结合车辆运行安全性指标提出了地铁线路的钢轨波磨安全限值以指导钢轨打磨。 LIANG 等［5］研究了车轮材料疲劳失效对车辆运行安全的影响， 从而提出了钢轨打磨标准。 江万红等［6］探究了曲线波磨区段轮轨系统动态响应， 并基于轮重减载率和轮轨垂向力确定了钢轨打磨限值。 CHOI 等［7］研究了不同波长和波深轨道不平顺与车辆运行安全性之间的关联性， 进而提出了轨道不平顺的限值。 张鹏飞等［8］和ZHANG 等［9］分析了不同特征钢轨波磨对轮轨系统动力响应的影响规律， 提出了指导钢轨打磨的波深安全限值。 XU 和ZHAI［10］通过车辆动力学性能的可靠性评估研究了钢轨波磨的打磨标准。 张富兵等［11］根据车轴许用应力和轮轨垂向力的限值要求提出了打磨限值。

综上所述， 前期对地铁线路钢轨打磨限值的研究大多从车辆运行安全性的角度出发， 没有综合车辆安全性和波磨发展趋势考虑钢轨打磨限值。 本文作者结合重庆地铁十号线的现场调研， 首先建立车辆-轨道系统动力学模型， 结合车辆运行安全性评价指标提出钢轨波磨的安全限值。 然后建立典型波磨区段轮轨系统有限元模型， 研究轮轨系统摩擦耦合振动特性， 并从波磨发展趋势提出钢轨波磨的波深打磨限值， 为山地城市地铁运营单位钢轨打磨治理提供数值参考。

1 仿真模型与分析方法

1.1 车辆-轨道系统动力学模型及安全性评价

为确定钢轨波磨的安全限值， 文中结合车辆安全性评价指标， 探究山地城市地铁在平纵曲线交叠区段的动态响应特性。 首先， 根据现场调研建立了相应区段的车辆-轨道系统动力学模型， 如图2 所示， 其建模参数如表1 所示。 车辆为山地城市地铁As 型列车，行驶速度约为70 km／h， 钢轨为CN60， 轨距为1 435 mm， 轨底坡为1／40， 线路包括直线段L1-缓和曲线段L2-圆曲线段L3-缓和曲线段L4-直线段L5， 各段长度分别是100、 85、 540、 85、 100 m， 曲线半径设置为500 m， 超高设置为110 mm， 坡度设置为35‰。结合平纵曲线交叠区段的钢轨波磨特征， 在动力学模型中采用单一的谐波函数模拟钢轨波磨， 如公式（1） 所示［12］。 钢轨波磨的波长范围为30 ～70 mm，波深范围为0.02 ～0.20 mm。 由于车辆-轨道系统动力学特性受随机轨道不平顺的影响很小， 因此这里不考虑随机轨道不平顺［13］。

表1 As 地铁动力学模型基本参数Table 1 Parameters of the vehicle-track system dynamic model

式中：Z0（x） 为轨道不平顺；D为波深；L为波长；x为行驶位移；n为激扰波数。

此外， 参考车辆安全性评价指标的限值规定［14］，轮轨垂向力P、 轮轨横向力Q、 轮轴横向力H、 线路横向稳定性系数C和轮重减载率R如式（2） — （6）所示， 各评价指标安全限值如表2 所示。

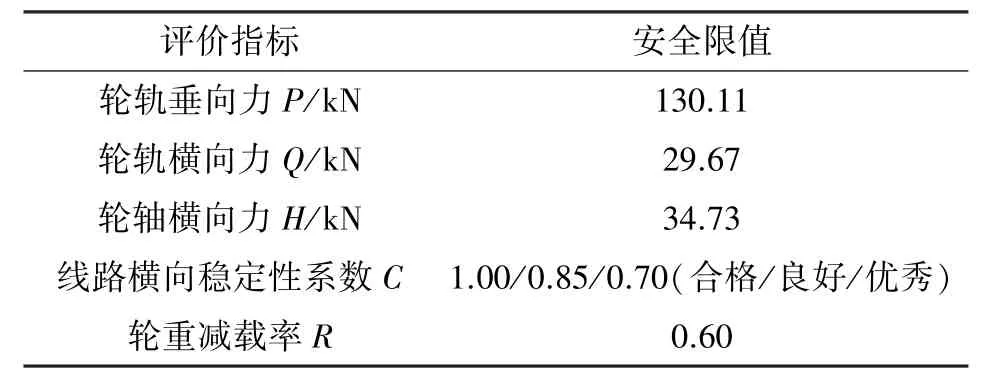
表2 车辆运行安全性评价指标安全限值Table 2 Evaluation index safety limits of vehicle operation safety

式中：Pst为静轮载；P0为车辆静轴载；QL和QR分别为轮对左、 右轮的轮轨横向力；PL和PR分别为轮对左、 右轮的轮轨垂向力。

1.2 轮轨系统有限元模型及摩擦耦合振动分析

为实现钢轨波磨的精准控制， 选取了50 mm 波长的典型钢轨波磨， 从波磨发展趋势的角度进行轮轨系统的摩擦耦合振动分析研究， 从而提出精准的打磨限值。 首先， 利用有限元仿真软件ABAQUS 建立了典型钢轨波磨区段的轮轨系统有限元模型， 如图3 所示。 由于导向轮对在曲线段的动力学特性变化更为明显， 此处仅选择前转向架的导向轮对进行分析［15］。各结构材料属性设置为： 车轮、 车轴和钢轨的密度为7 800 kg／m3， 弹性模量为210 GPa， 泊松比为0.3［16］。 其中车轮滚动圆直径为840 mm， 车轮踏面为LM 磨耗型踏面， 车轮与钢轨间的摩擦因数设为0.4［17］， 轮轨接触位置由动力学计算所得的横移量和接触角进行调整。 扣件采用弹簧-阻尼单元模拟， 其间距为625 mm， 扣件的垂向刚度为40.73 MN／m，横／纵向刚度为8.79 MN／m， 垂向阻尼为9 898 N·s／m，横／纵向阻尼为20 000 N·s／m［18］。 另外， 低轨分为松弛区和波磨区， 其中波磨区长度为1.875 m， 并设置了波长为50 mm 的典型钢轨波磨不平顺。 利用python 提取并修改该区段钢轨表面的节点坐标， 以此模拟钢轨波磨不平顺。 需要注意的是， 此处采用单一谐波函数模拟钢轨波磨不平顺， 假设其沿钢轨纵向变化， 而不随钢轨横向变化。

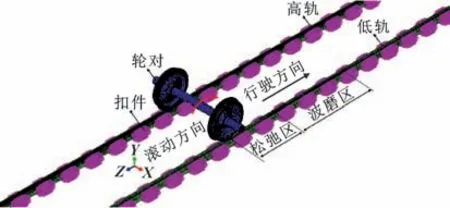
图3 轮轨系统有限元模型Fig.3 Finite element model of wheel-rail system

利用有限元软件ABAQUS 提供的显示动态分析程序ABAQUS／Explicit， 对轮轨系统瞬时动态响应进行分析［19-20］。 ABAQUS／Explicit 采用中心差分法对运动方程进行显式时间积分， 在t时刻的节点加速度为

式中：为节点加速度； ［M′］ 为质量的对角线集中矩阵；FP（t） 为系统外力；FI（t） 为系统内力。

然后采用中心差分法对时间进行显式积分：

式中： Δt为时间标量。

最后通过应变变化率计算出单元应变增量dε，从而计算系统在（t＋Δt） 时刻的应力σt＋Δt：

根据应力计算系统在（t＋Δt） 时刻的内力FI（t＋Δt） ， 进而将该内力代入下一个时间增量的计算。

2 结果与讨论

2.1 车辆-轨道系统动力学分析

通过车辆-轨道系统的动力学分析， 掌握钢轨波磨特征对车辆-轨道系统动力学特性的影响规律， 进而结合车辆服役安全性评价指标提出安全限值。 车辆-轨道系统动力学分析结果如图4 所示， 可以发现轮轨系统动态响应随着钢轨波磨波深的增大而增大，随着波长的增大而减小。 对比五项安全性评价指标在不同特征钢轨波磨下的变化趋势， 其中轮轨垂向力和轮重减载率增大最为明显， 而轮轨横向力、 轮轴横向力和线路横向稳定性系数变化相对滞后， 这表明钢轨波磨变化时， 轮轨垂向力和轮重减载率更为敏感。 根据安全性评价指标的超限情况， 绘制了钢轨打磨安全限值曲线， 如图5 所示。 波长为30、 40、 50、 60、 70 mm 的波深安全限值分别取0.03、 0.04、 0.05、0.08、 0.15 mm。

图4 不同波长和波深下车辆-轨道系统动力学分析结果Fig.4 The results of vehicle-track system dynamic analysis at different wavelength and corrugation depth： （a） wheel-rail vertical force；（b） wheel-rail lateral force； （c） wheelset lateral force； （d） wheel unloading rate； （e） lateral stability coefficient of line

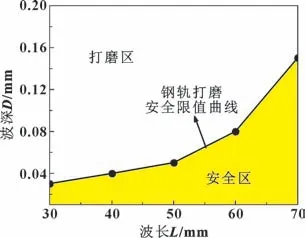
图5 不同波长下的钢轨波磨安全限值Fig.5 The safety limits of rail corrugation with different wavelengths

2.2 轮轨系统摩擦耦合振动分析

结合轮轨系统有限元模型， 采用瞬时动态分析研究典型钢轨波磨对轮轨系统摩擦耦合振动特性的影响， 提出其打磨限值。 首先， 轮轨接触力直观地反映了列车通过波磨区时轮轨系统摩擦耦合振动特性， 其时程图如图6 所示。 从整体来看， 波磨区不同波深对应的轮轨接触力变化趋势一致， 且随着波磨波深的增大而增大， 当波深由0.01 mm 增长到0.05 mm 时，轮轨接触力最大值增长幅度为23.34%。 然后对波磨区的轮轨接触力进行时频分析， 其时频图如图7 所示。 轮轨接触力的主频在400 Hz 左右， 其能量最大值随着波深的增大而增大， 并在波深为0.02 ～0.03 mm 时增长速率最大。

图6 不同波深下的波磨区轮轨接触力时程图Fig.6 The time-history diagram of wheel-rail normal force in the corrugated area under different rail corrugation depth

图7 不同波深钢轨波磨影响下能量最大值及波磨区轮轨接触力时频图Fig.7 The maximum energy values and time-frequency diagram of wheel-rail normal force in the corrugated area under different rail corrugation depth

轮轨接触力从全局的角度观测了轮轨系统的摩擦耦合振动特性， 然后通过钢轨表面振动加速度从局部的角度分析轮轨系统的摩擦耦合振动特性。 文中选取低轨上波磨区的测点＃A 进行分析， 钢轨表面垂向加速度a的时间历程曲线及其峰-峰值A随着波深d的变化情况如图8 所示。

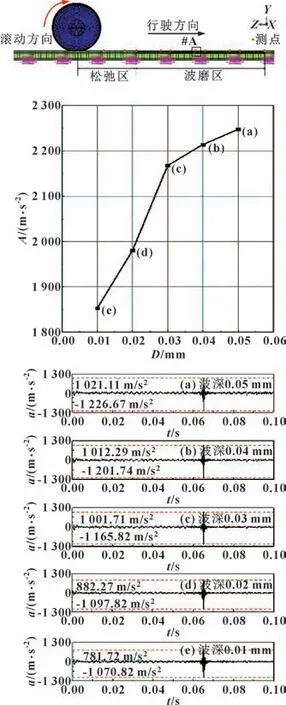
图8 钢轨表面垂向加速度及其峰-峰值Fig.8 The normal acceleration of rail surface and its peak-peak values

钢轨表面垂向加速度峰-峰值随着波磨波深的增大而增大， 波深由0.01 mm 增长到0.05 mm 时， 钢轨表面垂向加速度峰-峰值增大了17.58%， 且在0.02～0.03 mm 时增长速率最大。 对图7 所示的钢轨表面垂向加速度信号进行功率谱密度PSD 分析， 不同波深钢轨波磨影响下的钢轨表面垂向加速度的主频及其振动信号强度如图9 所示。 钢轨表面垂向加速度主频约为391.6 Hz， 其功率谱密度最大值随波深的增大而增大， 并在波深0.02 ～0.03 mm 时增长速率最大。 综合上述分析结果， 钢轨表面垂向加速度峰-峰值及其能量最大值和轮轨接触力能量最大值均在波深0.02～0.03 mm 时增长速率最大， 这表明在该区间轮轨系统摩擦耦合振动快速增大。 故将波长为50 mm典型波磨的波深打磨限值控制在0.02 mm 以下， 可以抑制轮轨摩擦耦合振动， 进而延缓波磨的发展， 为山地城市地铁运营单位提供打磨限值参考。

图9 钢轨表面垂向加速度的功率谱密度分析结果Fig.9 Power spectral density analysis results of normal acceleration on rail surface： （a） overall overview； （b） variation trend

3 结论

根据现场调研， 建立山地城市地铁平纵曲线交叠区段车辆-轨道动力学模型， 分析钢轨波磨特征对轮轨动态响应的影响规律， 并结合安全性指标提出钢轨波磨的安全限值。 然后建立典型波磨特征区段轮轨系统有限元模型， 研究轮轨系统的摩擦耦合振动特性，从波磨发展的角度提出波深打磨限值以指导打磨控制。 主要得到如下结论：

（1） 车辆服役安全性评价指标随着钢轨波磨波深的增大及波长的减小而增大。 综合安全性评价指标提出波长为30、 40、 50、 60、 70 mm 的钢轨波磨的安全限值分别为0.03、 0.04、 0.05、 0.08、 0.15 mm。

（2） 在典型波磨特征区段， 轮轨系统摩擦耦合振动随着波磨波深的增大而增大， 在波深为0.02 ～0.03 mm 时， 其增长速率均达到最大。 这表明该范围内钢轨波磨有更快的发展趋势， 应及时采取打磨措施。

（3） 控制典型钢轨波磨的波深打磨限值在0.02 mm 以下， 能有效抑制轮轨系统摩擦耦合振动， 延缓钢轨波磨发展， 为山地城市地铁运营单位进行钢轨打磨作业提供限值参考。