大展弦比太阳能无人机气动载荷计算方法研究

崔久红,张建刚,郑其浩

(1.航天特种材料及工艺技术研究所,北京 100074;2.中国航空工业集团公司第一飞机设计研究院,西安 710089;3.华中科技大学 航空航天学院,武汉 430074)

0 引言

载荷是飞机结构强度设计的重要输入参量,准确计算飞机在飞行中承受的载荷直接关系到飞机的安全性和经济性。太阳能无人机升阻比高、飞行速度低,机翼具有超大展弦比和较低的翼载荷[1]。结构设计是太阳能无人机的关键问题之一。实践中,超长航时的总体性能要求太阳能无人机的结构系数尽可能小、翼面轻薄和展弦比大。然而,大展弦比结构在飞行过程中不可避免发生大挠度变形[2],难以进行结构设计载荷的准确计算。

计算结构设计载荷需分别计算飞行载荷和地面载荷[3],飞行载荷需要计算的机动类型主要有稳定俯仰、急剧俯仰、滚转机动、偏航机动和阵风情况,其中稳定俯仰载荷是最主要的载荷,由其决定了大部分机体结构的设计,为此本文主要计算稳定俯仰工况的载荷。载荷计算需要大量数据,考虑数量繁多的不同工况,从工程实用角度出发,在飞机的初始设计阶段,按照规范要求可计算刚体飞机的载荷;在详细设计阶段,通过引入机体的刚度数据,进行弹性飞机载荷的计算。工程实际中,为了兼顾效率与精度,先采用简单快速的方法进行计算,再对关键的设计工况采用高精度的方法进行验算。按照工程实际设计情况,本文对大展弦比太阳能无人机气动载荷计算方法进行分析,并对某型大展弦比太阳能无人机计算结果进行验证,以期为工程实际应用提供借鉴。

1 刚体飞机载荷计算

飞行载荷计算需将规范中的要求转化为数学方程并求解,主要有两个步骤:第一步通过机动模拟计算飞机机动的时间历程及确定载荷计算状态参数;第二步是计算每一状态各个部件的载荷分布[4-5]。由于在方案阶段缺乏准确的机体刚度数据,对载荷具体数值的精度要求并不是非常高[6],因此可暂时忽略机体弹性,采用刚体飞机模型进行载荷计算。

1.1 飞行参数计算

稳定俯仰机动(也称为平衡机动)是假定升降舵以很慢的速率偏转,俯仰角加速度为零的一种极限情况,飞机总是处于平衡状态,且处于对称机动包线和包线内所有的点上。此时俯仰角速度应是与使用过载系数相应的限定俯仰角速度。稳定俯仰机动主要计算机翼、机身和水平尾翼等部件的强度。迎角和舵偏角可以通过求解如下代数方程得到[7]。

(1)

(2)

(3)

式中,g为重力加速度。

1.2 分布载荷计算

ωz和v可由参考文献[3]中获得,根据前述分析可得α和δe,在此基础上,可计算飞机的分布载荷。

分布载荷主要涉及结构惯性力和气动力的计算。其中,惯性力计算相对简单,可参考文献[8]进行。气动力计算比较复杂:涉及的状态数量巨大;舵面和副翼等活动面在行程范围内连续变化;涉及各种角速度。此外,气动力计算结果更关注的是法向气动力,且太阳能飞机飞行速度较低,为此,气动载荷采用涡格法[9]进行计算。把机翼在基本平面先沿展向分成若干列,然后再沿等百分比的弦线分成若干行,将整个翼面分成n个网格面元。在每个网格面元上布置一个马蹄涡,其附着涡线与该网格面元的四分之一弦线重合,每个马蹄涡的涡强为常值,不同网格面元上的涡强不同,形成涡格,建立涡格模型。升力作用点选在附着涡线的中点,每个涡格四分之三弦线的中点取为控制点,由毕奥-萨瓦公式计算出每个涡控制点处的下洗速度,下洗速度与来流速度的合成速度满足翼面上无穿透速度的边界条件。尾涡都与飞机轴线平行。当机翼平均弯度线斜率很小,迎角也较小时,边界条件近似为

(4)

式中:wm为下洗速度;vn为侧洗速度;φ为上反角;V∞为自由流速。由式(4)可得各个网格面元涡强。基于此由茹科夫斯基升力公式可计算每个网格面元上的升力,即可得到翼面的气动载荷分布。

载荷计算需要考虑诸多工况。涡格法计算较为简便快捷,需对其计算结果进行校核,为此,对不同的设计工况同时采用涡格法和计算结果较为准确的CFD法通过N-S方程进行求解,并对计算结果进行比较。图1和2所示为半翼展上均匀划分29个站位,每一站位采用两种方法计算所得机翼剪力和弯矩比较图。

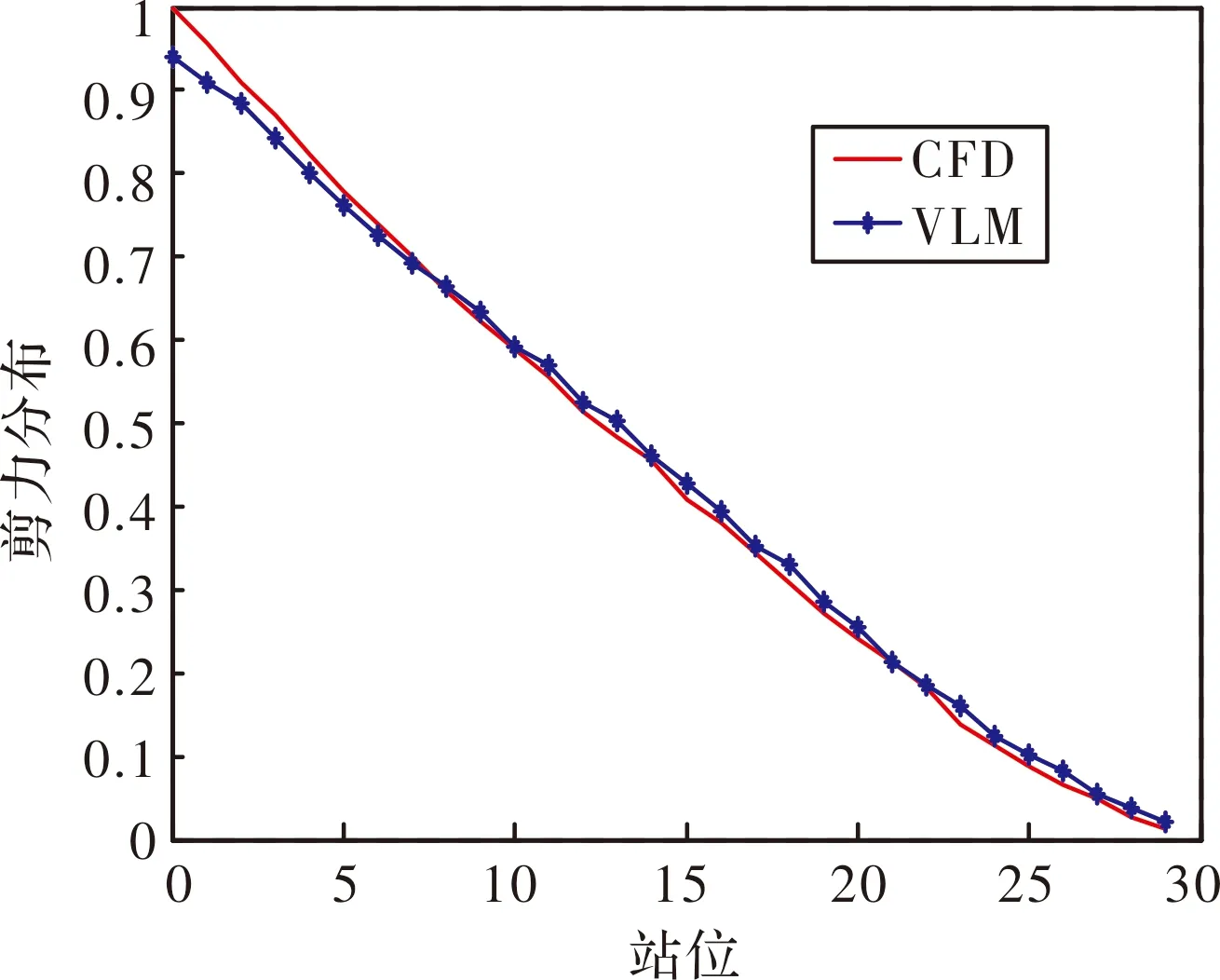
图1 机翼剪力对比

图2 机翼弯矩对比

从图1和2可见,采用涡格法计算的载荷分布与CFD结果吻合较好,表明涡格法载荷计算精度满足要求,可实际应用。

2 弹性飞机载荷计算

大展弦比机翼在飞行过程中可产生明显的弹性变形,会明显影响机翼的气动载荷分布,在载荷计算中必须予以考虑。机翼载荷计入弹性变形影响后可较为明显降低,可减轻机翼结构重量。稳定俯仰机动是一种对称机动,飞机在1 g平飞的初始状态下以很缓慢的速率偏转升降舵,俯仰角加速度为零,飞机总是处于平衡状态,变形对于结构固有频率的改变非常缓慢,可忽略变形引起的惯性力,因而该问题可用静气弹理论进行分析。

对于静气弹问题越来越多采用CSD/CFD耦合的方法研究机翼的静气动弹性响应问题。通常采用非结构动网格技术来适应迭代过程中的机翼变形,通过径向基函数法实现流固耦合面的数据交换[10-11]。CFD/CSD耦合的方法计算量大,工程上更多的是采用相对简化但满足工程要求的做法。较早的简化做法为:在刚性载荷的基础上,利用工程梁理论计算机翼的变形,用升力线理论计算变形引起的气动力增量,在这二者之间进行迭代直至收敛[12],这种方法物理概念清晰、计算速度快。近年来,这种方法仍广泛用于静气弹效应对机翼载荷大小及分布影响的计算分析[13-17]。在给定的飞行工况下,飞机结构的静平衡方程为[18]

(5)

(6)

式中:[G]为样条矩阵,将结构变形和气动网格的变形联系了起来。模态法中,结构变形采用模态叠加

{X}=[φe]{q}

(7)

式中:[φe]是弹性模态矩阵;{q}是模态坐标。将式(7)代入式(5)并左乘[D]T,可得

(8)

(9)

(10)

令:

(11)

3 算例

3.1 计算过程及结果

为验证上述方法的有效性和适用性,以某大展弦比太阳能无人机稳定俯仰后掠机翼载荷为例进行计算。计算条件为:飞机过载为2.5 g;速压为200 Pa。气动网格建立在机翼的中弧面上,以计入翼型弯度的影响。网格在前后缘及舵面处适当加密,如图3所示。

图3 气动网格

结构网格按机翼承载方式进行划分,网格密度根据计算结果需求确定,然后根据结构网格对模型进行模态分析,得到结构的弹性模态的振型。计算仅取前30阶,然后在结构节点中选取若干能够描述的振型节点,应用RBF函数,插值得出每一振型对应的气动网格的变形,即得到矩阵,如图4所示。

图4 气动网格模态插值

按照上述方法,在给定过载、俯仰角速度和俯仰角加速度的情况下,通过求解式(11)得到飞机的刚体自由度配平参数,将此参数代入式(7)和(10),即可得到结构的弹性变形。此工况的刚体自由度配平参数结果列于表1。

表1 配平参数对比

由表1可知,在给定的工况条件下,弹性体飞机的迎角显著降低。这是因为机翼弹性变形中存在较大的顺气流方向的扭转,导致飞机有效迎角增大,为满足过载要求,必须降低飞机刚体自由度的迎角。同时升降舵的偏转方向也有了变化,这是因为弹性变形后飞机的气动压心沿航向有变化所导致的。

根据式(11)计算得到刚体自由度配平参数及弹性变形的模态坐标,将这些参数作为气动载荷计算的边界条件代入式(4),即可进行分布载荷计算。不考虑结构变形得到的载荷为刚性载荷,结构变形影响的载荷为弹性载荷,将两种载荷的机翼的剪力和弯矩进行比较,结果如图5和6所示。

图5 机翼剪力对比

从图5和6可以看出,载荷计算中计入机翼弹性的影响后载荷数值降低较为明显,其中翼根的弯矩大约降低6%。将刚性个弹性载荷分别施加在飞机结构上进行有限元分析,得到结构的变形云图如图7所示。

图7 不同载荷下结构变形对比

从图7可以看出,在刚性载荷作用下,机翼最大挠度为7.4 m,在弹性载荷作用下此数值为6.1 m,最大挠度降低了大约18%,该结果与前述弯矩分析结果一致,随之机翼结构的应力也将会有较为显著的降低。

3.2 计算结果核对

3.1节的结构变形计算及气动力的计算方法均为相对简化的计算方法,为了验证计算结果的准确性,采用更准确的方法对少数关键工况弹性飞机载荷计算结果进行校核。气动力采用CFD计算,变形采用MSC.Nastran计算,所得结果分别示于图8和9。

图8 机翼剪力对比

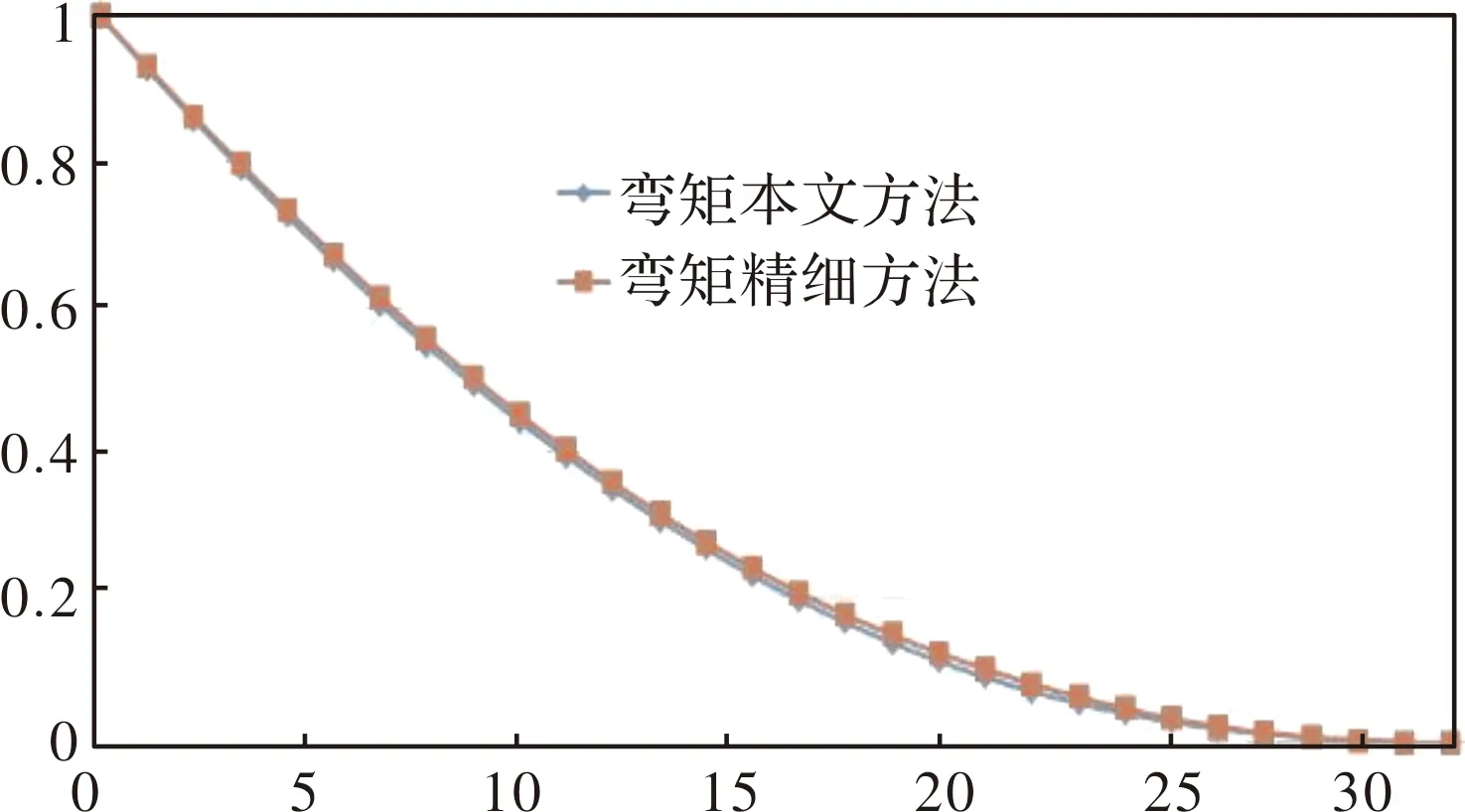
图9 机翼弯矩对比

从图8和9可以看出,本文计算方法与其他算法结果非常接近。实际上,CFD计算网格数量在千万数量级,MSC. Nastran计算大约为三百万,而本文中的方法气动网格数量约为五千,结构自由度仅为30,本文算法的计算量远小于其他算法。

4 结论

本文以某型大展弦比太阳能无人机为分析对象,以满足工程实际需求为出发点,在方案阶段计算了刚性飞机的结构载荷,在详细阶段计算了弹性飞机的载荷,主要结论如下:

(1)对速度较低的大展弦比飞机,采用涡格法计算气动载荷的分布可以满足工程需要;

(2)在详细设计阶段,采用涡格法和模态叠加法计算弹性飞机的载荷结果表明该方法可以应用于详细阶段的载荷计算;

(3)弹性飞机的载荷低于刚体飞机的载荷(幅度10%以内),在方案阶段采用刚性载荷是可行的,可加快研制进度。在详细阶段载荷计算计入弹性变形可显著降低机翼载荷,有利于结构减重;

(4)规范中规定的载荷情况还有急剧俯仰、滚转机动等,这些工况飞机在短时间内飞行参数变化较大,不宜采用静气弹的假设进行计算。