大展弦比复合材料机翼结构细节抗疲劳优化

雒卫廷

(吕梁学院物理系，山西 吕梁 033000)

大展弦比机翼留空时间长、航程远，所以高空长航时飞行器几乎都使用大展弦比机翼布局。大展弦比复合材料机翼是根据静强度设计准则进行设计，所受静载的强度符合要求。若设计时未考虑损伤容限/耐久性的设计原则，在实际应用时，大展弦比复合材料机翼结构的外翼下壁板便会出现裂纹情况[1]。大展弦比复合材料机翼结构出现裂纹情况表示结构细节抗疲劳性较低，出现该情况存在三种可能，一是下壁板缺口圆角制作不精细，二是此部位的使用载荷较大，三是出现裂纹的部位结构细节设计不达标[2]。

大展弦比复合材料机翼的结构设计及对飞机机翼的健康状态预测，目前已有部分研究，但对其结构的细节抗疲劳研究较少。其中，崔建国等[3]提出了基于多元经验模态分解(MEMD)和极限学习机(ELM)的飞机机翼健康状态预测方法。通过提取飞机机翼盒段健康状态的特征信息，结合其能量熵值对其健康状态进行有效预测。韩小进等[4]利用ANSYS有限元软件中几何非线性迭代方法，分析变截面梁受均布载荷时的变形。模拟实验发现所构建的有限元模型可以用于飞机机翼变形的模拟测试，减轻实际繁琐操作，但其可靠性有待进一步提高。Lai等[5]采用普朗特升力线理论(LLT)和赫尔姆博尔德面板法(HPM)分析机翼的结构性能，其利用阻力预测法(RDPM)计算机身阻力，将计算得到的升力和阻力系数进行比较，以验证计算结果的可靠性。研究发现，较大的机身直径有助于增加翼身组合的总阻力，而对升力没有显著影响。

鉴于当前研究中并未单独考察大展弦比复合材料机翼结构的细节抗疲劳性能，本文研究大展弦比复合材料机翼结构细节抗疲劳方法，将疲劳寿命以及结构质量设成目标函数，对大展弦比复合材料机翼结构进行优化，让飞机具备较高的抗疲劳强度。

1 大展弦比复合材料机翼结构细节抗疲劳问题研究

1.1 大展弦比复合材料机翼动力学原理

在分析大展弦比复合材料机翼动力学原理时，将大展弦比复合材料机翼中的阻尼材料模量看成常数，研究阻尼结构模态将其变形，并通过能量比获取大展弦比复合材料机翼结构的损耗因子估算值[4]。

通常情况下，大展弦比复合材料机翼结构离散后的自由振动方程是：

(1)

式中：x表示大展弦比复合材料机翼自由振动因子；大展弦比复合材料机翼结构的质量矩阵和刚度矩阵分别设成B、C。针对大展弦比复合材料而言，刚度矩阵C属于连续性复刚度矩阵。公式(1)的解变换为特征值的形式，则特征值Y是：

Y=φ*(j)

(2)

式中，φ*(j)表示大展弦比复合材料机翼在自由振动时的第j阶复特征向量，则变换方法是：

(3)

(4)

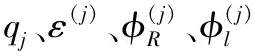
(5)

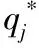
(6)

C=CR+Cl

(7)

其中，大展弦比复合材料机翼左侧结构刚度矩阵与右侧结构刚度矩阵依次设成Cl、CR。结合式(4)、式(6)和式(7)可知：

(8)

式中：q2(1+iε)表示大展弦比复合材料机翼的疲劳寿命矩阵；i表示扰动因子。ε能够根据复向量φ*运算获取；复向量φ*通过纯弹性分析获取[8]。将式(8)等号两侧实虚部分以此相等便能获取：

(9)

(10)

其中，q2表示大展弦比复合材料机翼自振频率的实数。若矩阵C是通过有限元分析获取，它便由Ce、Cv两部分构成。计算大展弦比复合材料机翼结构弹性单元便可获取Ce，计算粘弹性单元便可获取Cv，那么C可定义成：

C=Ce+Cv

(11)

其中，大展弦比复合材料机翼结构实数阵与复数阵分别设成Ce、Cv。针对仅存在单一种类的大展弦比复合材料结构而言，大展弦比复合材料虚部与实部的比例是εv∶1。εv表示大展弦比复合材料损耗因子，则有：

Cv=CvR+iCvI=CvR(1+iεv)

(12)

Cl=Cvl=εvCeR

(13)

则分析大展弦比复合材料机翼弹性模态时，应变能是：

U=φCRφ

(14)

大展现比复合材料机翼结构通过粘弹性层变形导致的模态应变能是：

Uv=φCvRφ

(15)

将式(9)和式(13)代入式(8)中，去除q2，则有：

(16)

最后将式(14)、式(15)代入式(16)中，获取大展弦比复合材料机翼结构的模态损耗因子ε(j)是：

(17)

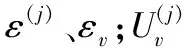
1.2 大展弦比复合材料机翼结构细节抗疲劳优化方法

基于上小节分析的大展弦比复合材料机翼结构的抗疲劳性能，根据简化原则，将大展弦比复合材料机翼结构中下壁板设成研究的主体，分析缺口圆角半径、材料厚度、下壁板厚度对大展弦比复合材料机翼结构危险方位的干扰[9]。所以，选择的3个设计变量是缺口圆角半径，y(1)，y(2)与y(3)分别表示大展弦比复合材料机翼厚度和机翼下壁板的厚度。

大展弦比复合材料机翼结构中疲劳危险部分主要处于下壁板倒角上[10]。通过修正诺伯法可知，此部位的局部应力、应变出于加载状态时的计算方法是：

(18)

其中：Δz描述名义应力增量；应力变程设成Δβ；大展弦比复合材料循环强度系数设成g；Δφ描述应变变程；大展弦比复合材料循环硬化指数与弹性模量依次设成n、A。

计算式(18)便可获取应力、应变变程，最后便可获取大展弦比复合材料机翼结构中细节疲劳位置的局部应力、应变值[11]。大展弦比复合材料机翼结构整体应变和寿命(循环数)间的关联性是：

(19)

其中，a、b表示大展弦比复合材料机翼结构的材料参数。A=72 571.94 MPa，n′=0.08，a=-0.072 7，b=-0.776 1，βi=884.646 MPa，g′=949.512 MPa。通过式(2)可知，若Δφ≥min，2ni≥max，所以将大展弦比复合材料机翼结构疲劳寿命的目标函数设成Δφ。

通过式(18)可求：

(20)

采用非变动的滞后环曲线计算应变时和此式仅存在系数差异[12]。式(20)为有关Δφ、Δz的隐函数，将此隐函数设成大展弦比复合材料机翼结构疲劳寿命的目标函数。式(20)直接迭代，未经收敛，便能够将其变形简化，则建立的收敛格式是：

Δφ=1.394×10-6(giΔz)2×

(21)

先设置一个Δφ，使用式(21)对Δφ实行迭代计算，直至符合要求的准确性便可结束。

式(21)中Δz表示名义应力增量值，gi表示大展弦比复合材料机翼结构疲劳缺口系数，这两者都属于设计变量(y(1),y(2),y(3))的函数，但判断存在一定难度。为简化计算，使用有限元程序拟合二者间的计算方式[13]。具体构建的有限元模型如图1所示。

图1 大展弦比复合材料机翼结构的有限元模型

有限元模型中，在划分网格时，依据所构建机翼各个部分结构的受力特性，将梁支柱和梁肋缘条划分为成杆单元，通过大展弦比复合材料机翼结构中下壁板异常处的6～7间肋间、第一与第二长桁的部分构建[14]。当中，大展弦比复合材料机翼结构中下壁板材料是LC4CS，将平面四边形单元，长桁、7肋、梳状件材料设成LY12CZ。按照飞机强度计算资料能够计算大展弦比复合材料机翼结构6和7肋上壁板的受力信息。采用线性插值方法计算大展弦比复合材料机翼异常区，研究剖面中的载荷状况。

基于缺口圆角半径y(1)、材料厚度y(2)以及下壁板厚度y(3)，采用有限元分析便可得知大展弦比复合材料机翼下壁板圆角处属于脆弱位置。但疲劳强度降低系数gi和名义应力间具有较高的关联性。名义应力属于设计变量与外在的函数。所以拟合giΔz和设计变量的曲线：

giΔz=0.884y(1)3+0.51y(2)3+0.18y(3)3-

7.77y(1)2-5.1y(2)2-4.2y(3)2+3.8y(1)+

11.9y(2)+23.66y(3)+0;016y(1)2y(2)-

0.015y(1)2y(3)-0.039y(2)2y(1)-0.113×

y(2)2y(3)-0.215y(3)2y(1)+0.053y(3)2×

y(2)+0.042y(1)y(2)y(3)+0.143y(1)y(2)+

3.39y(1)y(3)0.384y(3)y(2)+10.5

(22)

基于常幅疲劳载荷中分析大展弦比复合材料的瞬态行为，在缺口部位进入塑性时，便能够忽略复合材料的记忆效应。则对比优化大展弦比复合材料机翼结构的质量与原结构质量的结果是：

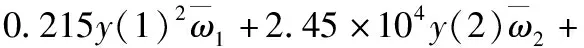
(23)

基于上述优化方法的计算，大展弦比复合材料机翼结构细节抗疲劳优化的数学模型是：

(24)

模型求解方法是先设置一个初始Δφ，让函数变成显函数，使用加权组合法把每项分目标变换为统一目标函数M(Y)：

(25)

式中，加权因子设成V，V>0，它的值通过容限加权判定，V1=0.836,V2=0.164。通过上述计算后，大展弦比复合材料机翼结构细节抗疲劳优化方法为：

(26)

其中，M(Y)表示大展弦比复合材料机翼结构的统一目标函数函数。使用参数型惩罚函数法建立增广目标函数ZG：

(27)

式中，ki(i=1,2,…)表示可自大变小的常数。若ki→0，便能获取设定Δφ时的问题最优解。则式(27)即为不存在约束优化的问题。通过Δφ的迭代，计算优化式(26)，符合迭代终止设定的Δφ值就是抗疲劳方法最优值。

2 实验分析

采用本文方法优化某大展弦比复合材料机翼结构的细节抗疲劳性能。优化后的结果见表1所示。

表1 优化结果

分析表1可知，使用本文方法优化后的大展弦比复合材料机翼结构危险部位应力是405.71 MPa，小于未优化前的应力，说明本文方法可以较好的使用材料性能，优化前的飞机重量为52 630 kg，优化后飞机重量为41 310 kg，飞机重量减轻，提升疲劳寿命，优化后的机翼寿命为10 484.93个小时，优化前的机翼寿命只有6 638.3个小时，验证了本文方法的有效性。

为了验证本文方法的性能优势，采用本文方法、基于响应面模型的结构疲劳寿命优化方法、等效结构应力法进行对比实验。

1)可靠性

飞机可靠性是指在规定条件下和规定时间内完成预定任务的能力，包括稳定性、耐久性和安全性。该指标是评价3种方法优化后的大展弦比复合材料机翼结构的安全性。设定10 000仿真次优化实验，分析3种方法的优化可靠性，其数据如表2所示。

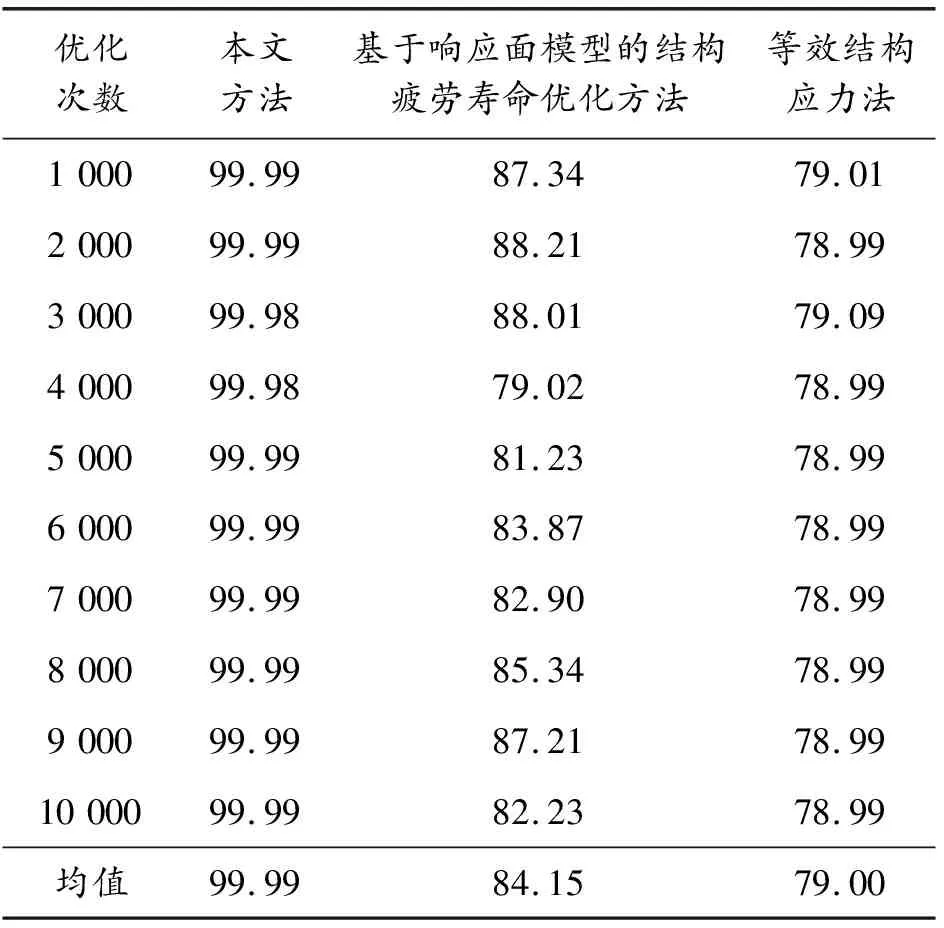
表2 3种方法的可靠性数据 %

分析表2可知，采用3种方法多次优化大展弦比复合材料机翼结构后，本文方法的可靠性是99.99%，基于响应面模型的结构疲劳寿命优化方法、等效结构应力法的可控性均低于90%。说明本文方法优化后的大展弦比复合材料机翼结构抗疲劳性能好，可靠性高。

2)飞行时间

采用3种方法多次优化大展弦比复合材料机翼结构的细节抗疲劳性，并对比3种方法优化后的机翼运行时间，如表3所示。

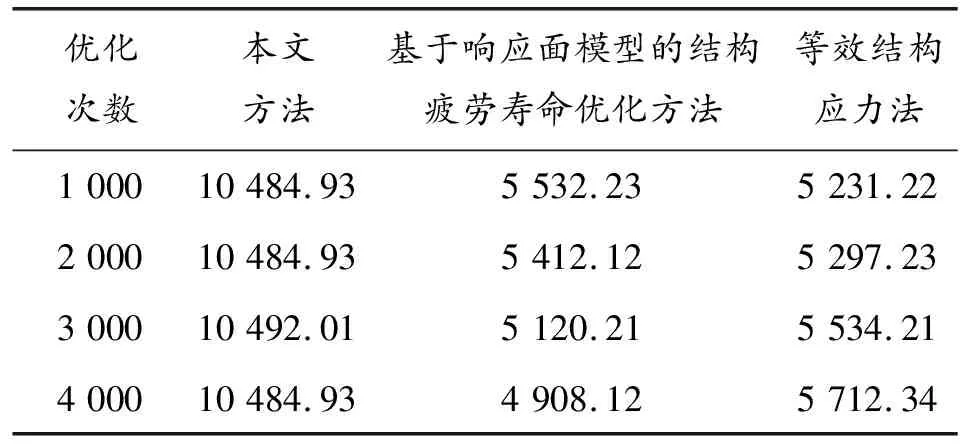
表3 3种方法优化后大展弦比复合材料机翼飞行时间 h

续表(表3)

分析表3可知，多次优化后，本文方法优化后的大展弦比复合材料机翼飞行时间最大值是10 492.01 h，基于响应面模型的结构疲劳寿命优化方法、等效结构应力法优化后的大展弦比复合材料机翼飞行时间始终小于本文方法。由此可知，本文优化后的大展弦比复合材料机翼结构细节抗疲劳性能较好，机翼飞行时间较长。

3 结论

本文研究的大展弦比复合材料机翼结构细节抗疲劳方法经过实验验证。本文方法优化后的机翼，飞行时间高达10 484.93个小时，与同类优化方法相比，本文方法的可靠性与好评率都超过90%，性能显著优于同类优化方法。