怎么做能帮助学生更好地理解假分数
2023-06-29王蝶凤
教学月刊(小学版) 2023年17期
□王蝶凤
假分数是分数教学中的一个难点。为了帮助学生更好地理解假分数的含义,可以采用以下教学过程。
一、回顾旧知,引入分数度量的意义
1.教师用课件出示两条线段(如图1),并提问:如果线段①的长度是1米,那么你估计线段②的长度是多少?

图1
2.教师用课件动态演示用线段②去测量线段①的过程(如图2),得出线段②的长度正好是线段①长度的,也就是1米的,所以线段②的长度是米。

图2
二、探究新知,经历假分数的产生
1.估一估。教师在图1 下方出示线段③(如图3),请学生估一估线段③的长度。学生发现线段③比线段①长,长度大于1 米,但具体长度需要测量。
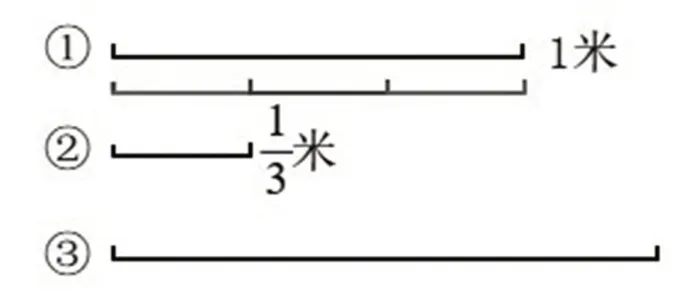
图3

图4
三、观察比较,突破“假”在哪里
1.做一做。教师出示另外三条线段,引导学生用刚学的方法量一量它们的长度。学生量出三条线段的长度分别为米。
2.比一比。学生观察、比较各个分数,概括假分数的含义:分子比分母大或分子和分母相等的分数叫作假分数。教师提问:假分数是分数吗?引导学生得出:假分数是大于1或等于1的分数。
3.想一想。教师提问:假分数与整数、真分数之间有什么关系?引导学生发现就是就是可以看作由相加形成的数。由此可以看出:有些假分数的分子恰好是分母的倍数,它们实际上是整数;有些假分数的分子不是分母的倍数,这样的假分数可以写成带分数。
四、多元表征,完善假分数的意义
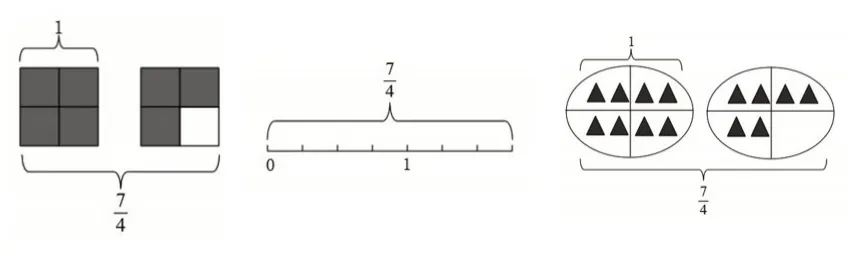
图5
在操作中,学生体会到,可以把一个图形、一个计量单位或者一些物体看成单位“1”,把单位“1”平均分成4份,每一份是它的,7个就是
五、数轴演变,拓宽分数的含义
教师将线段演变成数轴,引导学生在数轴上找到上述的这些分数,发现真分数和假分数各自的区间(如图6),建立分数意义与分数大小之间的联系。

图6
整个教学过程中,学生经历了假分数产生的过程,深入理解了假分数也是分数,从而对分数意义有了更完整的认识。
