热颤振地面模拟试验技术

2023-06-27陈浩宇王彬文宋巧治李晓东

航空学报 2023年8期

陈浩宇，王彬文，宋巧治，李晓东

中国飞机强度研究所航空声学与振动航空科技重点实验室，西安 710065

高超声速飞行器机动性高、航程远、毁伤能力出色，具有重要的战略意义与极高的军事价值，是当前各国研究的热点。由于飞行马赫数较高，高超声速飞行器在飞行过程中除了气动载荷外还会承受严酷的气动热载荷，热载荷与气动力、结构弹性力、惯性力相互耦合作用，进而引发热颤振问题。

作为高超声速飞行器面临的一种典型气动弹性问题，热颤振对飞行器的飞行安全具有重要影响，近年来国内外均对此开展了广泛的研究。在理论分析方面，研究人员在早期单向热耦合假设的基础上进一步研究了热颤振双向耦合分析方法，如Culler 和Mcnamara［1］通过简支平板算例证明了在大约束力条件下双向耦合计算模型的优势，杨超等［2］通过壁板颤振分析对比了不同耦合模型在计算结构温度分布及颤振边界时的精度差异。此外随着计算机技术的发展，计算流体力学方法也被逐步应用于热颤振分析中，如Lamorte 和Friedmann［3］采用径向基函数将湍流模型引入热颤振求解器，探究了考虑湍流效应对热颤振分析结果的影响。在试验验证方面，能够满足热颤振研究需求的主要手段为超声速风洞试验技术，但该技术实施难度较大，目前相关研究较少，且仍处于方法探索层面，如季辰等［4］采用加热气流对翼板结构开展的高超声速热颤振风洞试验研究。

综上，虽然针对热颤振理论分析方法的研究已取得诸多进展，但由于理论分析中难以准确考量真实结构存在的非线性、阻尼特性等因素，计算结果的可信度难以保证，因此后续的试验验证对于热颤振研究而言具有重要意义。然而，目前由于高超声速飞行器热颤振风洞试验实施困难、温度分布与实际存在较大差异等问题，研究人员尚未建立一种能够满足型号验证需求的热颤振试验验证手段，这给高超声速飞行器研制工作造成了一定阻碍，因此亟需一种在工程层面上可行的试验验证技术，弥补当前热颤振研究方法的不足。

飞行器地面颤振模拟试验技术是一项采用真实结构作为试验对象的半实物仿真验证技术，能够有效规避颤振理论分析中无法考虑结构非线性、阻尼特性的问题，对理论分析结果能起到很好的补充验证作用［5］。该技术理念最早由Kearns［6］在1962 年提出，潘树祥和齐丕骞［7］在20 世纪80 年代即对热颤振地面模拟试验技术进行了初步探索。随着计算机技术及控制技术的发展，在21 世纪初俄罗斯的Smyslov 等［8-9］及美国的Zeng 等［10］先后提出了较为完整的地面颤振模拟试验方案并进行了试验验证。近年来国内也针对该项技术开展技术攻关，如许云涛等［11］对非定常气动力模拟方法开展了研究，Wang 和Fan［12］提出了基于计算流体力学（Computational Fluid Dynamics，CFD）降阶模型的非定常气动力模拟方法；在试验系统控制方面，吴志刚等［13-14］分别采用PI 控制器及前置反馈补偿方法针对导弹及平板翼面设计了试验系统控制器，宋巧治等［15-16］则采用鲁棒控制算法设计试验系统控制器，并采用风洞机翼模型进行了试验验证。

由于地面颤振模拟试验技术以地面振动试验（GVT）系统为基础，具有较强开放性，因此本文通过在现有试验系统基础上增加热试验设备模拟气动热效应，实现热环境下结构的颤振测试，从而将常温颤振地面模拟试验技术推广至热颤振研究领域［17］。由于气动加热效应，结构的固有特性及颤振特性会发生变化，因此热颤振系统具有显著的时变特性［18］，传统的针对时不变系统的气动力模型和颤振边界测试方法不再适用。为此，本文将对引入时变温度场的地面颤振模拟试验技术开展研究，并进一步完成地面热颤振模拟试验系统集成与验证，论证该项技术的可行性。

1 地面颤振模拟试验原理

飞行器地面颤振模拟试验技术的核心思想是采用激振设备模拟结构在飞行过程中承受的非定常气动力，进而达到颤振边界测试的目的。在试验过程中，系统通过传感器测量结构的振动响应信号，将其代入预先获得的非定常气动力降阶模型从而得到结构应承受的等效气动力，然后采用激振器将等效气动力实时加载到结构上，并通过控制算法确保气动力的精确加载。最终通过对试验结构施加初始扰动并观察其响应，实现对真实结构颤振边界的测试，试验系统如图1所示。

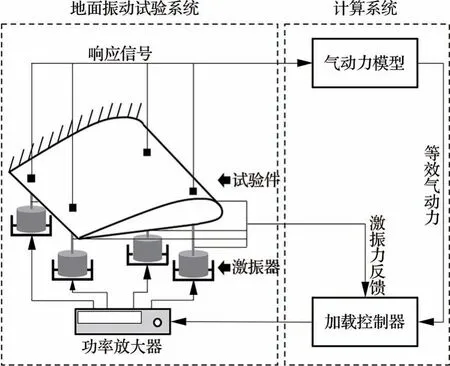
图1 地面颤振模拟试验系统Fig.1 Ground flutter simulation test system

2 研究对象

2.1 试验件

试验件选择为如图2 所示的切尖三角形翼面结构，其根弦长1 800 mm，梢弦长150 mm，半展长1 200 mm，前缘线与根弦的夹角为31°，厚度9 mm，通过螺栓与钢梁底座连接模拟根部固支边界。

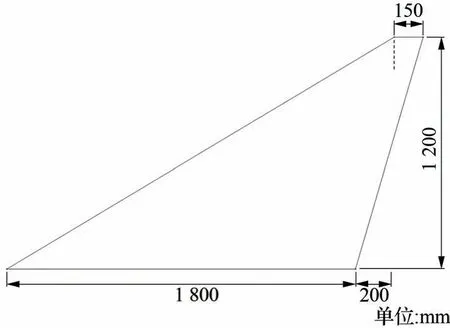
图2 翼面几何尺寸Fig.2 Geometrical size of the wing

试验件材料选为TA15 钛合金，其密度为4 450 kg/m3，泊松比为0.39。由于本文需要考虑温度对结构动力学特性的影响，因此表1 给出了部分TA15 材料参数随温度变化的数据。

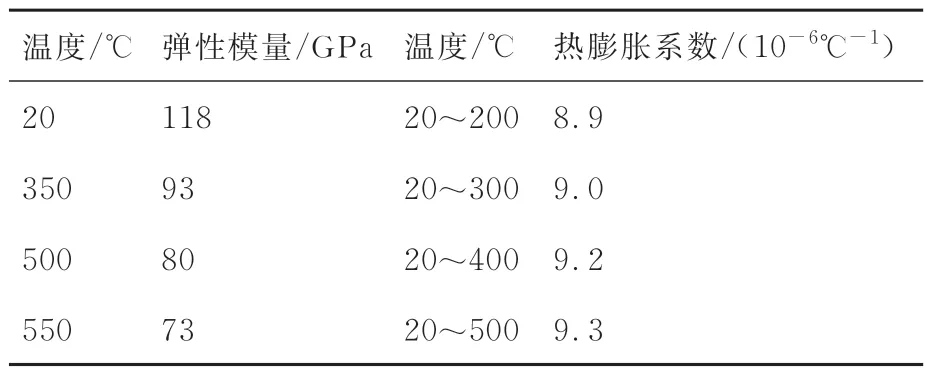
表1 TA15 材料参数Table 1 Material parameters of TA15

2.2 气动加热环境分析

实际的高超声速飞行器飞行轨迹较为复杂，本文为了简化问题，将飞行环境设定为海拔高度21 km，并以3.8Ma（Ma为马赫数）速度飞行。

采用FLUENT 和NASTRAN 进行气动加热及传热计算。采用松耦合的方式进行分析，获得结构在上述飞行状态下的稳态温度场如图3 所示，其中最高温约为490 ℃，最低温约为160 ℃。为了便于试验开展，设定结构初始均匀温度场为50 ℃，时变历程中结构各温区温度匀速上升，温升时长为110 s。

图3 结构稳态温度场Fig.3 Steady temperature field of structure

2.3 模态及颤振特性分析

针对上述时变温度环境下的结构，本节分析工作采用时间冻结假设，在2.2 节设定的温度时变历程中均匀采样，选取12 个工况点进行热模态数值计算。计算从温度对材料弹性模量的影响以及不均匀温度场造成的结构热应力2 方面考虑了温度对结构模态特性的影响，相关计算参数已在表1 中给出。结果显示，在初始温度场下结构主要参与颤振的第1、2 阶模态频率分别为7.5 Hz与24.1 Hz，而在最终稳态温度场下这2 阶模态频率分别降至5.4 Hz 与14.5 Hz。结构在这2 种不同温度场下的第1、2 阶模态振型如图4 所示。

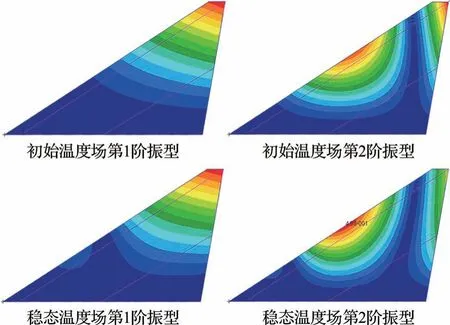
图4 结构前2 阶热模态振型Fig.4 The first 2 mode shapes of structure

根据上述不同工况点下的热模态数据开展颤振分析，获得12 个工况点的第2 阶模态分支速度-重力加速度（v-g）曲线如图5 所示。结果显示，在翼面结构由初始温度场升至稳态温度场的过程中，其颤振临界速度由2 776 m/s 降至1 221 m/s，颤振频率由19.7 Hz 降至11.1 Hz。

图5 第2 阶模态v-g 曲线Fig.5 v-g plot of the 2nd mode

3 非定常气动力模拟

在地面颤振模拟试验中，需要根据结构响应实时计算非定常气动力并施加给结构，因此非定常气动力的计算精度对试验结果影响显著。同时由于热颤振系统中结构的时变特性影响，原有非定常气动力模拟方法难以满足试验需求，因此需要研究可用于时变温度场试验系统的非定常气动力模拟方法。

3.1 考虑多工况的气动力等效插值点优化

由于设备尺寸等条件的限制，试验首先要对气动力模型进行降阶处理，从而实现通过少数插值点准确模拟分布非定常气动力的目标。此类气动力插值点优化问题的本质是一个离散点的最优化选取问题，对此目前相关研究中通常采用基于广义力等效的遗传算法进行优化求解。

广义力等效优化方法的基本思想是寻找一个插值点布置方案，使得采用该方案时，插值点处的广义力与热颤振发生时结构承受的广义气动力误差最小，即此时在插值点处施加的集中力与结构实际承受的分布式非定常气动力在颤振分析中可视为等价关系。文献［11］经过推导得，该目标等效于通过优化所得插值点表示的气动网格插值振型与气动网格原始振型之间的偏差最小，考虑到各阶模态对颤振的贡献度差异，优化目标可表示为

式中：ηj为j阶模态对颤振的贡献量；NM为主要模态数量；NA为气动网格结点数量；φij与φij＇分别为缩减前后的气动力插值振型。obj 越小，说明缩减前后插值振型更接近，气动力模拟精度更高。

上述基于广义力等效的优化算法从颤振发生原理的角度出发设定优化目标，在地面颤振模拟试验方案设计中通常能够获得较为可靠的激振点/拾振点优化结果。但由式（1）可以看出，该优化方法采用的缩聚前气动力插值目标振型是固定的，即该优化结果仅是当前模态振型下的最优插值点，而在时变温度场中，结构的热模态振型也会随时间发生改变，这会导致不同时间节点下的最优插值点有所不同，而试验过程中激振点/拾振点位置不能改变，因此需要对现有函数进行调整。

对于受气动加热影响的结构而言，其温度场分布形式相对固定，因此在发生热屈曲前结构随温度变化的热模态振型不会突变，即在结构温度场单调递增（或单调递减）的过程中，结构模态振型中振幅较大区域的移动趋势基本保持不变。综上，可以选取结构温度变化曲线中的极值点作为典型工况点，例如对于本文中温度单调递增的试验系统而言，即为工况1（初始温度场）与工况12（稳态温度场）。考虑所有典型工况点的热模态振型进行加权综合优化，在式（1）的基础上构建目标函数如下

式中：NC为选取的典型工况数量。如上文所述，当某组插值点对于2 个相邻的典型工况为综合最优方案时，则该组插值点即为这2 个典型工况点之间所有工况点的综合最优方案。因此，当某组插值点为所有典型工况的综合最优方案时（即obj最小时），该组插值点即为受热结构在整个时变过程中的最优激振点/拾振点布置方案。

3.2 基于Kriging 模型的非定常气动力建模

在采用3.1 节所述方法获得激振点/拾振点布置方案后，即可将经计算所得作用于激振点处的集中力fs在颤振模拟中等效替代结构实际承受的分布式非定常气动力，而该模拟气动力fs可通过式（3）求解

式中：q∞为来流动压；k=ωb/V为减缩频率，b为参考长度，ω为正弦振动频率，V为来流速度；zs为拾振点位移。Gf与Gz分别为描述节点气动力与位移缩聚关系的插值矩阵，对于本文所采用的翼面结构而言可以通过无限平板样条（Infinite Plate Splines， IPS）理论［19］获得。A(k)为气动力影响系数（Aerodynamic Influence Coefficient，AIC）矩阵，对于超声速颤振问题可以采用超声速偶极子格网法［20］获得，(k)为经过缩聚插值矩阵处理后的降阶气动力影响系数矩阵。

通常，气动力影响系数矩阵是在频域建立的，为了使半实物仿真试验能够实现，需要将频域气动力影响系数矩阵(k)转换到时域，为此采用最小状态法对其进行有理函数拟合，可得

将式（4）代入式（3）并做拉氏反变换，即可得到可用于试验的时域气动力模型如下

式中：s为拉普斯算子；R为气动力滞后根对角阵；A0、A1、A2、D、E均为采用最小状态法得到的系数矩阵。

在热颤振系统中，由于气动热效应会改变结构的模态特性，式（3）中描述拾振点位移与气动力缩聚关系的插值矩阵Gf、Gz不再是固定值，进而使降阶后的AIC 矩阵(k)发生变化，最终导致通过有理函数拟合所得的系数矩阵不再是固定值。从提升试验精度的角度出发，系统在试验进程的每一个时间步长都应采用式（3）～式（5）求解一次当前时间节点下的相关矩阵参数，从而建立适用于时变温度场中结构的非定常气动力模型，但这种方法显然无法满足地面颤振模拟试验对气动力计算效率的要求。为了兼顾气动力模型的计算精度与效率，本文引入Kriging 代理模型构建此类非定常气动力模型［21］。

Kriging 代理模型是一种基于随机过程的均方误差最小的无偏估计模型。以式（5）中任一时变系数矩阵元素Aij(t)为例，在任意时刻t，其对应的值被随机函数(t)代替，Aij(t)只是该随机函数可能的结果之一，即

式中：fn(t)为基函数；βn为每个基函数的系数；Z(t)是均值为0，方差为的静态随机过程。

将建模所采用的n个样本点定义为

则采样时间点之外的模型输出值可由样本点数值线性加权得到

其中：ct为加权函数向量，考虑Kriging 模型无偏估计且均方误差最小的要求，构建ct的求解方程如下

式（8）即为采用Kriging 模型表示的任意时刻的气动力影响系数矩阵参数，此时式（3）～式（5）的求解过程被简化为数个低阶矩阵计算，能够满足试验对时变系数矩阵计算效率的要求。

3.3 时变颤振边界跟踪测试方法

在时不变系统地面颤振试验中，通过不断调整气动力模型中的风速参数，观测不同风速下的系统响应，即可确定结构的颤振临界速度，但在热颤振研究中结构的颤振临界速度具有时变特性，上述采用固定风速值进行试验的颤振边界获取方法将不再适用。为此，本研究将PID（Proportion Integration Differentiation）控制器引入试验系统，提出一种颤振边界实时跟踪方法，以满足热颤振地面模拟试验的需求。

在试验中人为调整风速参数寻找被测结构颤振边界的逻辑可以概括为：结构响应发散则降低风速，结构响应收敛则增高风速。如果将结构响应幅值变化趋势定义为λ（λ＞0 为响应发散，λ＜0 为响应收敛），则显然速度修正量ΔV应与λ保持负相关关系，本节所述颤振边界实时跟踪方法即希望通过PID 控制器实现上述参数修正过程，而其中最关键的工作是将结构响应幅值变化趋势进行量化，以便PID 控制器识别。

地面颤振模拟试验中结构的响应信号可近似看作幅值持续变化的正弦信号，可表示为A(t)sinωt。为获取响应幅值变化趋势，首先应获得振动响应的幅值信号A(t)，对原信号做幅值采样所选取的时间点应满足式（10）

此时采样获得的信号为反映响应信号幅值的阶跃信号，但该信号由于噪声等扰动因素并非单调变化。为了增加控制系统的稳定性，需要排除此类信号局部扰动，使控制器在最大程度上关注幅值整体变化趋势，为此采用滑动平均法对信号做平滑处理，如式（11）所示

至此已将结构响应信号A(t)sinωt转化为描述结构响应幅值整体变化趋势的连续信号(t)如图6 所示。考虑到实际试验中的信号质量，直接对(t)作微分处理获取幅值变化趋势信号λ(t)会降低系统稳定性，此处设定一个较小的时间间隔Δt，将λ(t)描述为

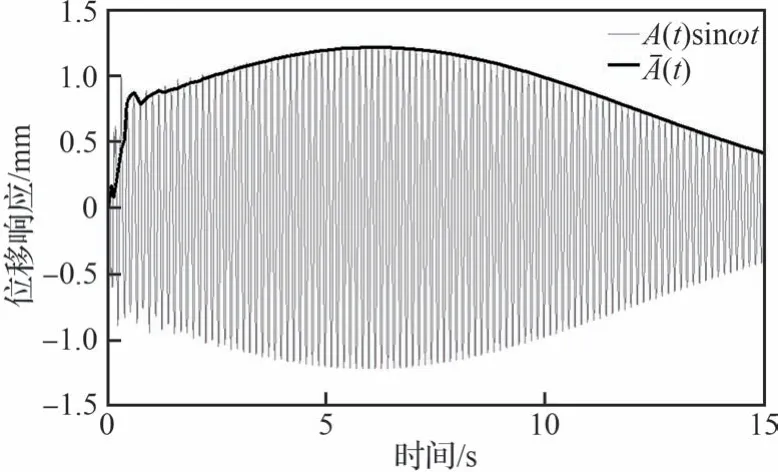
图6 响应信号幅值Fig.6 Amplitude of response signal

式（12）所获得的λ(t)即可定量描述结构响应幅值的变化趋势，在试验系统构建中即可将其作为PID 控制器的参考信号，通过在前期仿真及预试验中根据系统响应对控制器参数进行调整，即可实现热颤振地面模拟试验中的颤振临界速度实时跟踪。

3.4 仿真验证

本节采用第2 节所述翼面结构颤振系统作为仿真算例，验证上述针对时变热颤振系统的非定常气动力模拟方法。

首先对翼面结构进行激振点/拾振点优化，为便于计算及后续试验开展，此处设定激振点与拾振点共点。由于本算例中温度场变化趋势是持续升高，因此如3.1 节所述选取工况1 与工况12 作为典型工况采用式（2）进行考虑模态振型加权的插值点优化，得到最优插值点位置如图7所示。

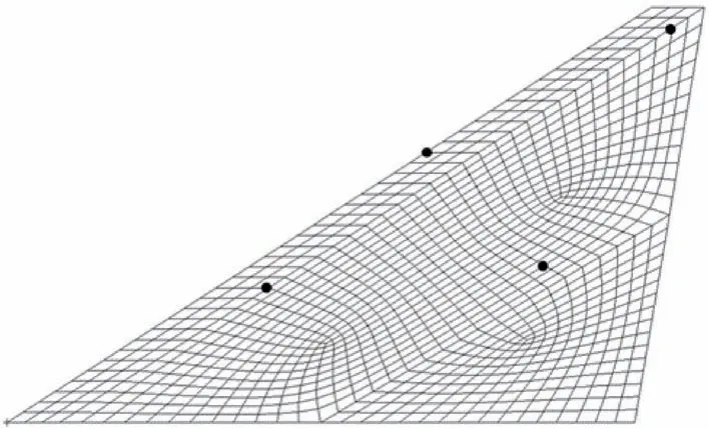
图7 考虑模态振型加权方法下的最优位置Fig.7 Optimal locations by weighting of modal shape

为了对比优化效果，额外选取工况1、工况7与工况12 分别采用式（1）所示广义力等效方法进行单工况优化。将4 组优化结果分别代入12 个工况，计算插值点缩减前后插值振型的差异度评价值如图8 所示。从全工况差异度的角度出发，选用工况1 与工况12 的单工况点优化效果比较差，只能保证选取的参考工况临近的工况点插值振型差异度较低；选用工况7 的单工况点优化效果与综合优化效果接近，在工况6～8 下其差异度还低于综合优化结果，这一现象也符合3.1 节的分析：在升温过程中结构模态振型中振幅较大区域的移动趋势基本不变，因此处于时变过程中间位置的工况7 最优节点组合更容易满足其他工况点插值振型低差异度的要求，但是考虑整个时变过程后显然采用模态振型加权优化方法能获得最优结果。

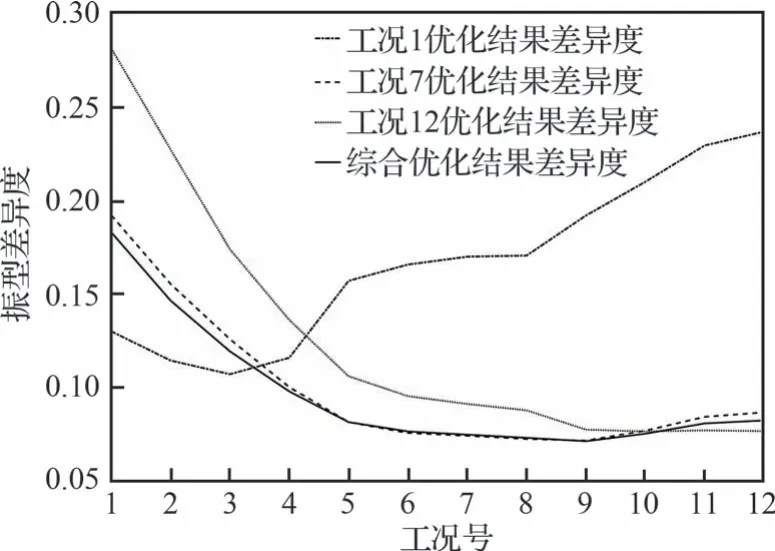
图8 不同节点组合下的振型差异度Fig.8 Diversity factors of different locations

根据3.2 节及3.3 节所述方法建立非定常气动力计算模块，并采用状态空间表示法建立结构响应计算模块，组成地面颤振模拟试验仿真平台如图9 所示［22］。

仿真时段与第2 节设定保持一致，总时间历程为110 s，速度跟踪模块在仿真开始后5 s 接入系统，其初始输出值设定为2 400 m/s。仿真所得速度跟踪曲线如图10 所示，其中三角形标记为数值计算所得该时刻采样工况点的颤振临界速度。将速度跟踪曲线稳定后各个工况点处的数值计算结果与仿真结果进行对比，可得仿真误差最大不超过4%，说明本文提出的非定常气动力模型及颤振速度跟踪方法能够有效应对热颤振系统的时变特性，可以用于热颤振地面模拟试验中。

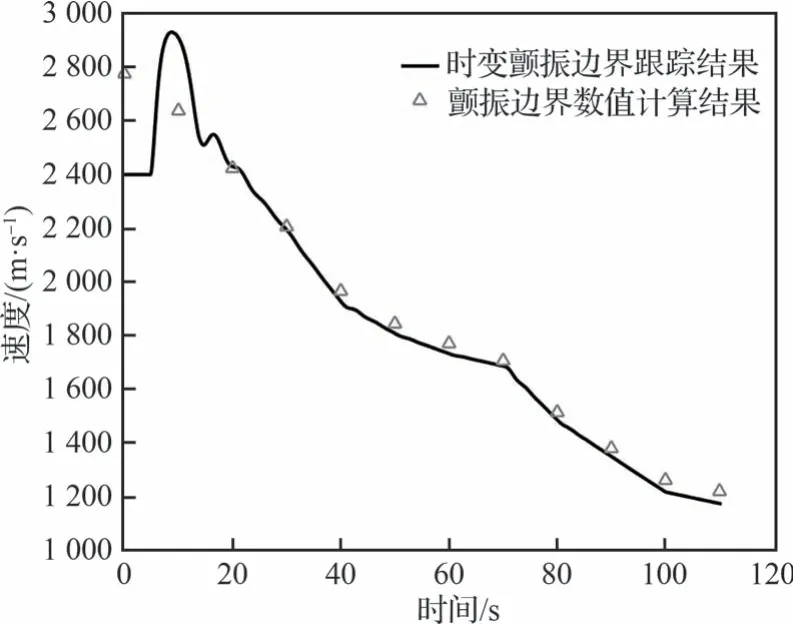
图10 仿真所得速度跟踪曲线Fig.10 Velocity tracing result obtained with simulation

4 试验系统

4.1 气动热环境模拟

试验采用石英灯辐射加热方式模拟结构承受的具有时变特性的气动热环境，加热系统由石英灯管辐射加热器、热电偶、加温控制仪、可控硅等组成，如图11 所示。加热系统工作原理可概括为：系统通过布置于被测结构表面的温度传感器获取测点温度，加温控制仪根据测得温度与预设温度计算加载修正量并通过可控硅调整石英灯加热器功率，实现温度场的闭环控制。

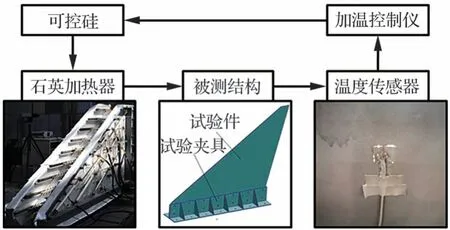
图11 气动热环境模拟系统Fig.11 Aerodynamic heating simulation system

由于结构承受的气动加热温度场具有大梯度分布的特征，因此在综合考虑试验设备能力后，将翼面划分为8 个加热温区1～8，翼面两侧温区对称布置，加热方案如图12 所示。根据试验设定的温度边界条件，加热方案为先将结构整体预热至50 ℃，加热时间为110 s，其中1/5 与2/6 温区为一组，并始终保持同温，温升速率均为4 ℃/s，3/7 温区温升速率为2 ℃/s，4/8 温区温升速率为1 ℃/s，最终达到翼板沿弦向分布的3 组温区的温度分别为490 ℃、270 ℃与160 ℃。

图12 试验结构加热方案Fig.12 Heating scheme for test structure

为评估上述加热方案所得结构实际温度场与数值计算所采用温度场的一致性，采用该加热方案开展热模态试验，并将试验测得前3 阶模态频率与2.3 节数值计算模态频率对比如图13 所示，可知各阶模态频率一致性较好，误差最大不超过7%，说明该气动热环境模拟方案的精度能够满足后续试验需求。

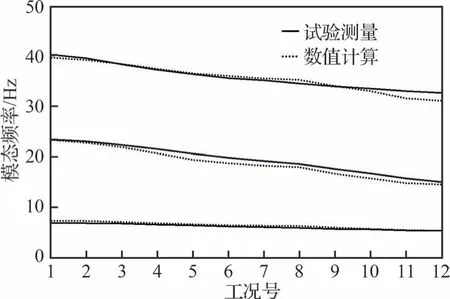
图13 热模态试验数据与数值计算结果Fig.13 Thermal modals test data and numerical results

4.2 响应信号测量

热颤振地面模拟试验需要在试验进程中同时获得测点的位移、速度、加速度信号，此时如果采用不受高温环境影响的激光测振仪作为唯一的信号采集设备［23］，就需要把测得的速度信号做积分处理以获得位移信号，微分处理以获得加速度信号，而在实际试验中由于高温场中热辐射光、烟雾以及气体受热密度变化导致光的折射等影响，激光测振仪信噪比较差，此种处理方法会造成位移信号出现显著零飘，加速度信号扰动较大，难以满足数据计算需求。

为了获得满足试验需求的高质量结构响应信号，本文参考吴大方等［24］在超高温热模态试验技术研究中的方法，选用外径5 mm 内径3.8 mm 的95%氧化铝空心陶瓷杆将结构响应信号引出高温环境，材料密度为3.75 g/cm3。陶瓷杆底部采用螺接的方式固定于结构测点处，如图14 所示。由于陶瓷杆顶部处于常温环境，因此可以布置常规加速度传感器及激光位移传感器测量响应信号。

图14 试验测点构造Fig.14 Test measuring-point construction

虽然文献［24］已经证明由于陶瓷杆刚度大密度小，其引入的附加质量对结构模态特性的影响不大，但地面颤振试验关注的是结构的振动响应，因此还需要对陶瓷杆动响应信号传递能力进行验证。分别在陶瓷杆顶部与底部安装加速度传感器后对结构进行扫频，扫频范围覆盖被测结构前2 阶模态频率（1～30 Hz），测得加速度响应信号如图15 所示。由扫频试验结果可知，二者信号相位完全一致，仅信号幅值在部分频段有细微差别，说明陶瓷杆的引入不会为试验系统在关注频带内引入新模态，且其能够较为准确传递结构响应信号，因此陶瓷杆能够在地面热颤振模拟试验中被用于传递结构响应信号。

图15 扫频响应信号对比Fig.15 Comparison of swept-frequency response signal

4.3 激励力加载控制

在地面颤振模拟试验中，激振器之间会通过被测结构相互影响，为了降低这种耦合效应导致的激励力加载偏差，本研究采用H∞鲁棒控制算法针对多激振器加载系统设计控制器［15］。

首先建立被控对象的状态空间模型。建模以扫频试验数据为基础，采用子空间辨识法进行，即首先构建输入输出信号的Hankel 矩阵，再将该矩阵斜投影并奇异值分解获得系统的可观测矩阵及卡尔曼状态序列，最后通过最小二乘法等算法即可获得系统状态空间矩阵。

为了简化控制器设计工作，将混合灵敏度设计方法引入标准H∞控制问题如图16 所示，在确定3 个加权矩阵W1，W2与W3后，即可通过Riccati方程或线性矩阵不等式（LMI）完成控制器求解。

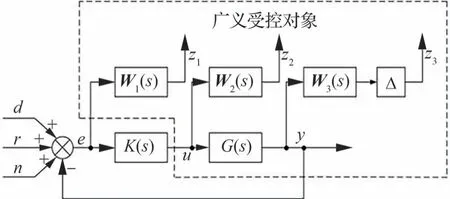
图16 混合灵敏度标准H∞控制问题Fig.16 Mixed sensitivity standard H∞ control problem

5 试验测试与结果分析

将气动热环境模拟系统与地面颤振试验系统集成开展试验，其中采用激光位移传感器测量节点位移信号并微分获得速度信号，采用加速度传感器测量节点加速度信号，非定常气动力计算及鲁棒控制算法由N（INational Instruments）半实物仿真系统实现。图17为热颤振地面模拟试验现场。

图17 热颤振地面模拟试验现场Fig.17 Thermal flutter ground simulation test site

试验初始空速设置为2 800 m/s，在试验开始约5 s 时开启颤振临界速度跟踪系统，试验所得结构监测点响应与颤振临界速度曲线如图18所示。

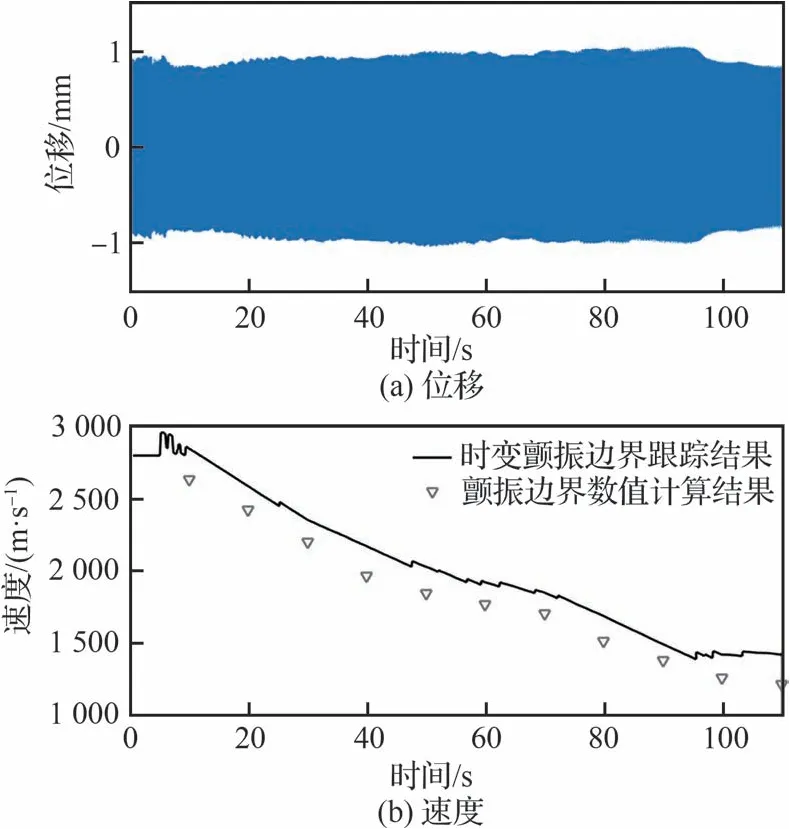
图18 热颤振地面模拟试验结果Fig.18 Thermal flutter ground simulation test result

由图18 可以看出，结构响应幅值整体变化不大，近似于等幅振动，且速度曲线时变趋势与图9所示本试验系统的仿真结果基本一致，说明颤振临界速度跟踪模块在试验系统中运行正常。值得注意的是，由3.3 节可知该速度跟踪模块是根据已有的结构响应信号变化趋势判断试验速度修正量，其修正过程具有一定滞后性，因此图18中结构响应并非理想情况下的等幅振荡，而是在10～90 s 间的缓慢发散以及90～110 s 间的缓慢收敛。参考此类地面颤振模拟试验中结构响应收敛或颤振发散的时间尺度［16］，这种极其缓慢的结构响应变化说明试验速度与结构实际颤振临界速度非常接近，并不影响颤振临界速度跟踪模块输出结果的可信度。

选取工况点所处时间点的速度跟踪数据（即10 的整数倍处时间节点）并与对应工况点的数值计算结果（图中三角形标记点）作对比，如表2所示。

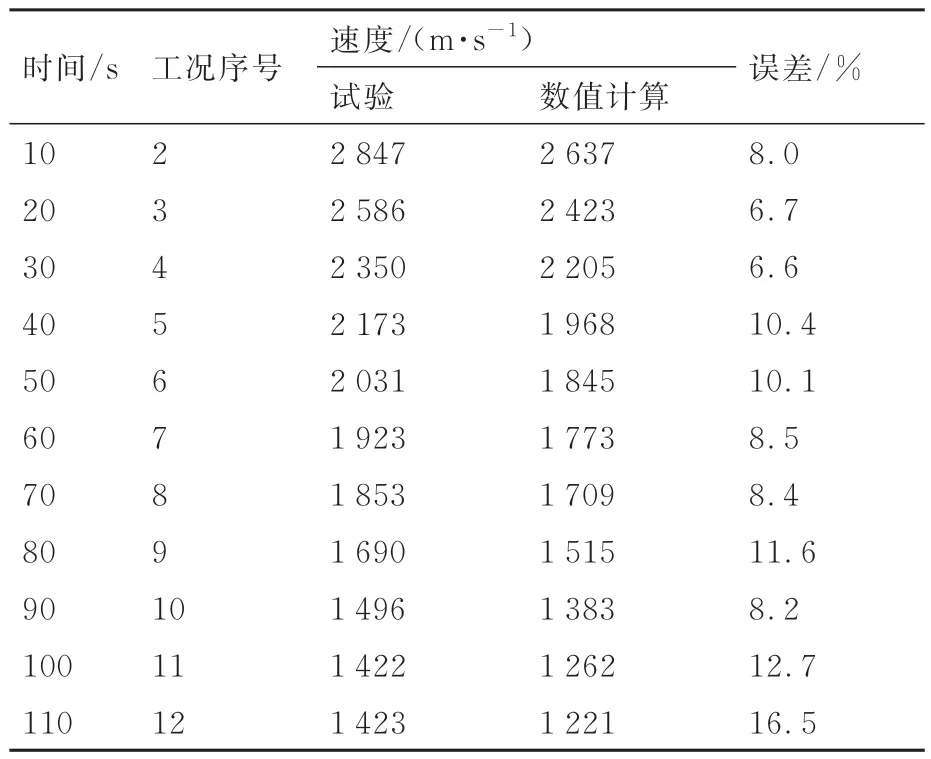
表2 试验结果及误差Table 2 Test results and errors

由表2 可知，试验所得颤振临界速度整体大于数值计算结果，由于颤振数值计算中未考虑结构阻尼，试验结果整体偏大是合理的，但是由于二者间误差处于较高水平，为进一步优化地面热颤振模拟试验技术，提升试验精度，对可能导致较大误差的原因分析如下：

1）本次试验仍然沿用了目前在地面颤振模拟试验中普遍采用的鲁棒控制器作为激励力控制方法。对于热颤振系统而言，随着温度升高结构动力学特性会发生显著改变，颤振频率显著降低，在应对此类动力学系统时鲁棒控制器存在2 个缺陷：一是鲁棒控制器求解采用的单一状态结构辨识模型难以反映系统在整个时变历程中的动力学特性；二是鲁棒控制器存在控制频带较窄的固有缺陷，因此当结构颤振频率改变至控制器控制频带之外时，力加载精度会显著下降，在试验进程后期（100～110 s）由于系统颤振频率已经偏离控制器设计频带，由表2 可以看出，此时试验误差显著增大。综上所述，鲁棒控制器的固有缺陷使其并不能完全满足热颤振地面模拟试验中的力控制要求，从而导致了较大的试验误差，因此针对热颤振地面模拟试验的气动力精准加载技术还值得进一步研究。

2）考虑到石英灯加热系统的加载偏差，实际试验中结构的温度场与数值计算采用的并不完全一致，虽然由热模态试验可知该温度场模拟偏差在误差允许范围内，但仍会对最终试验结果造成一定影响；此外，由于热试验系统与地面颤振试验系统相互独立，试验过程中需要人工操作实现2 套系统的并行，其运行的时间差会导致数值计算与实际试验的温度场不一致。对于热颤振系统而言，其颤振临界速度对温度场变化是较为敏感的，因此温度场与气动力模型的匹配误差也会为试验最终结果引入一定误差。