自适应Walsh 函数有限体积方法
2023-06-27任炯王刚胡国栋石晓露
任炯,王刚,胡国栋,石晓露
西北工业大学 航空学院,西安 710072
在航空航天领域的流动数值模拟中,为了精细刻画流场中存在的激波、涡系和剪切层等复杂流动结构,一般需要采用较高精度的数值格式和足够细密的计算网格来保证流场求解的分辨率[1]。实际流动问题中,复杂流动结构往往只出现在流场的局部区域,若全局性地加密网格或者提升格式精度,则会在流场参数变化相对平缓的区域引入“富余”的离散精度,带来不必要的计算消耗。为了解决这一问题,计算流体力学(Computational Fluid Dynamics,CFD)工作者们发展了各种类型的自适应求解技术,其主要思想是依据流场结构特征自动调整网格尺度或流场变量的离散阶次,通过离散精度和分辨率在流场中的合理配置,有效控制流场数值模拟的计算成本[2]。
依据实现策略的不同,流场自适应求解技术大致分为h 型、r 型和p 型3 类[3]。h 型自适应技术[3-11]是通过对原计算网格进行加密剖分和粗化聚合来实现网格疏密的调整,自适应过后,计算网格单元的尺寸、数量和拓扑关系均会发生变化;r 型自适应技术[12-13]一般是根据流场信息如变量梯度,通过移动网格节点来调整网格的疏密分布,其特点是在自适应前后网格的拓扑结构保持一致;p 型自适应技术[14-18]则固定网格单元尺寸和节点位置不变,通过局部增减插值/重构多项式的阶次来实现求解精度的合理配置。这3 类流场自适应求解技术与有限差分、有限体积或有限元等主流CFD 数值离散方法相结合,能够有效平衡计算精度与计算效率之间的矛盾,发挥兼顾高分辨和高效率等多方面的优势。因此,自适应求解的思想在CFD 领域获得了广泛的关注和大量的应用[3,9,13-15,17]。
近期,笔者所在研究小组,利用具有间断属性的Walsh 基函数所构造的级数对控制单元内的流动变量进行分片连续的离散表达,提出了一种具备网格内部捕捉间断能力的高分辨率Walsh 函数有限体积方法(The Finite Volume Method with Walsh Basis Functions,FVM-WBF)[19-20]。该方法以Walsh 基函数系数为解变量,在有限体积框架下,进行网格单元内的空间离散,形成关于解变量时间导数的半离散常微分方程系统,然后结合时间推进格式完成求解。在这个框架内,使用足量的Walsh 基函数能够显著提高流场模拟的数值分辨率,达到在网格内部对激波和涡系等流动结构精细刻画的效果。然而,在所有网格单元内统一增加基函数数目来提高分辨率会使得计算量呈几何倍数增长,计算效率显著下降。
为了在提高FVM-WBF 方法分辨率的同时,有效改善其计算效率,本文考虑引入基函数数目的自适应策略,根据流场特征对网格单元内的Walsh 基函数数目进行动态调整,仅在激波、涡系等流场变化剧烈的局部区域使用足量的Walsh基函数,而在其他区域维持相对少量的Walsh 基函数,避免基函数的全局性增加所引起的计算量爆发式增长。
本文首先对FVM-WBF 方法的基本原理和数值特性进行简要回顾,然后描述自适应策略在该方法中的具体实现过程,最后通过若干数值算例对新发展的自适应Walsh 函数有限体积方法(简称自适应FVM-WBF 方法)的分辨率和计算效率进行测试。
1 FVM-WBF 方法
以式(1)给出的积分守恒型二维Euler 方程为求解对象,对FVM-WBF 方法进行简要介绍。
式中:
其中:V=[u v]T,u和v分别为x和y方向上的速度分量;ρ、p和E分别为密度、压强和单位体积总能;Q为守恒变量矢量;F(Q)为无黏数值通量;Ω为求解域中的某一控制体;∂Ω为控制体边界;n为控制体边界处单位外法线矢量。为方便描述,这里用标量符号Q统一代表守恒变量ρ、ρu、ρv和E。
FVM-WBF 方法采用具有间断属性的Walsh基函数对控制体Ω内的守恒变量进行级数逼近:
式中:下标(m,n)由2 组对应一维Walsh 基函数的下标按照张量积顺序给定。一维Walsh 基函数是某个区间上定义的在1 和-1 之间频繁跃变的间断函数,可由定义域上的简单方波gn(x)=1按照不同层级经过二分演化生成,其具体的定义公式见文献[19-22],此处不赘述。
式(2)中的cm,n(t)是与基函数gm,n(x,y)对应的系数。根据一维Walsh 基函数的分类方式[19-22],二维Walsh 基函数gm,n(x,y)可由式(4)进行层级划分:
式中:p1和p2分别表示2 个一维Walsh 基函数gm(x)和gn(y)的所属级别。
为直观理解,图1 给出了单位正方形区域[0,1]×[0,1]上p=0, 1, 2 所对应的前3 级二维Walsh 基函数示意。图中的蓝、红色部分分别表示基函数的正负值所对应的子区域。可以看到,二维Walsh 基函数表现出与一维Walsh 基函数类似的特点:①具有等幅方波属性;②当基函数级别p≥1 时,各子区域随基函数级别p的提高分别在x和y方向递进二分,形成新的1/2p尺度的子区域,且正负值区域面积始终保持相等,这使得第p(p≥1)级的基函数在前p-1 级基函数形成的各子区域上的面积分均为0。
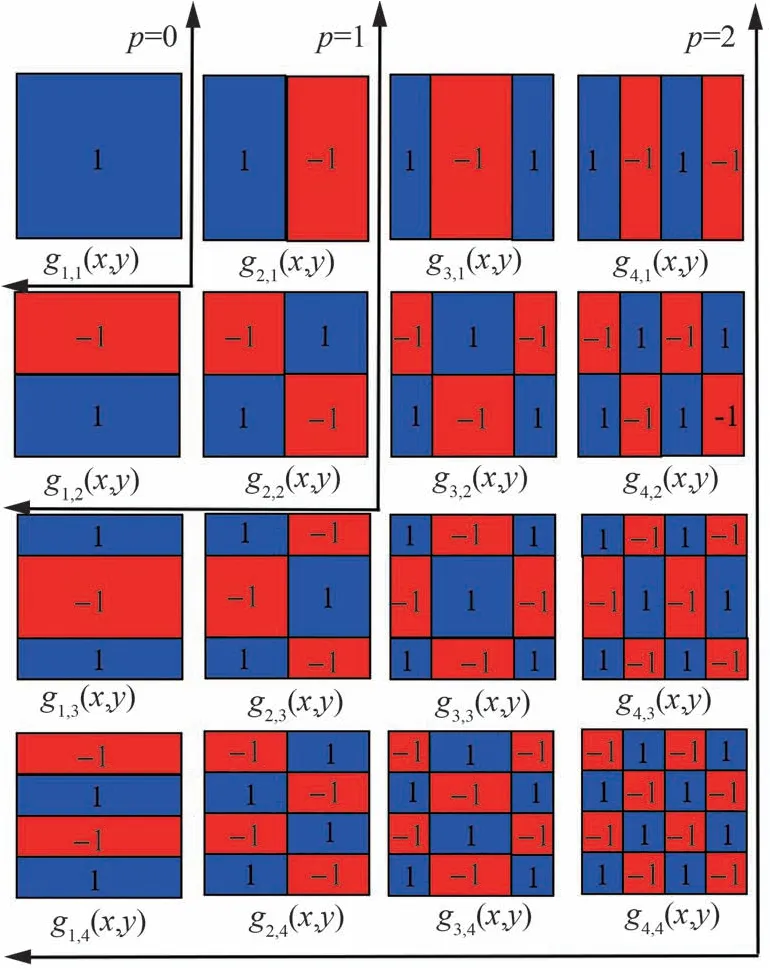
图1 单位正方形区域上的前3 级二维Walsh 基函数(g(1,1)(x,y)~g(4,4)(x,y),p=0,1,2)的取值示意图Fig.1 Schematic diagram of values of the first three groups of two-dimensional Walsh basis functions on unit square area (g(1,1)(x,y)~g(4,4)(x,y), p=0,1,2)
由Walsh 基函数的上述数学特点可以导出级数式(2)具有2 方面的数值特征:①在定义域上,守恒变量被描述成与基函数数目相同的分片连续区域上的离散形式,基函数数目越多,对变量的描述越精细;②级数式(2)具备良好的“伸缩”数值特性,由低级别向高级别级数式延伸或由高级别向低级别级数式收缩时,级数式伸缩前后的重叠部分所对应的系数可以直接继承原先的取值。接下来,以单位正方形网格[0,1]×[0,1]上的解析变量函数
为例,采用由图1 中的基函数形成的级数式(2)对其进行数值逼近,利用所获得的结果(见图2)演示级数式(2)的上述数值特性。
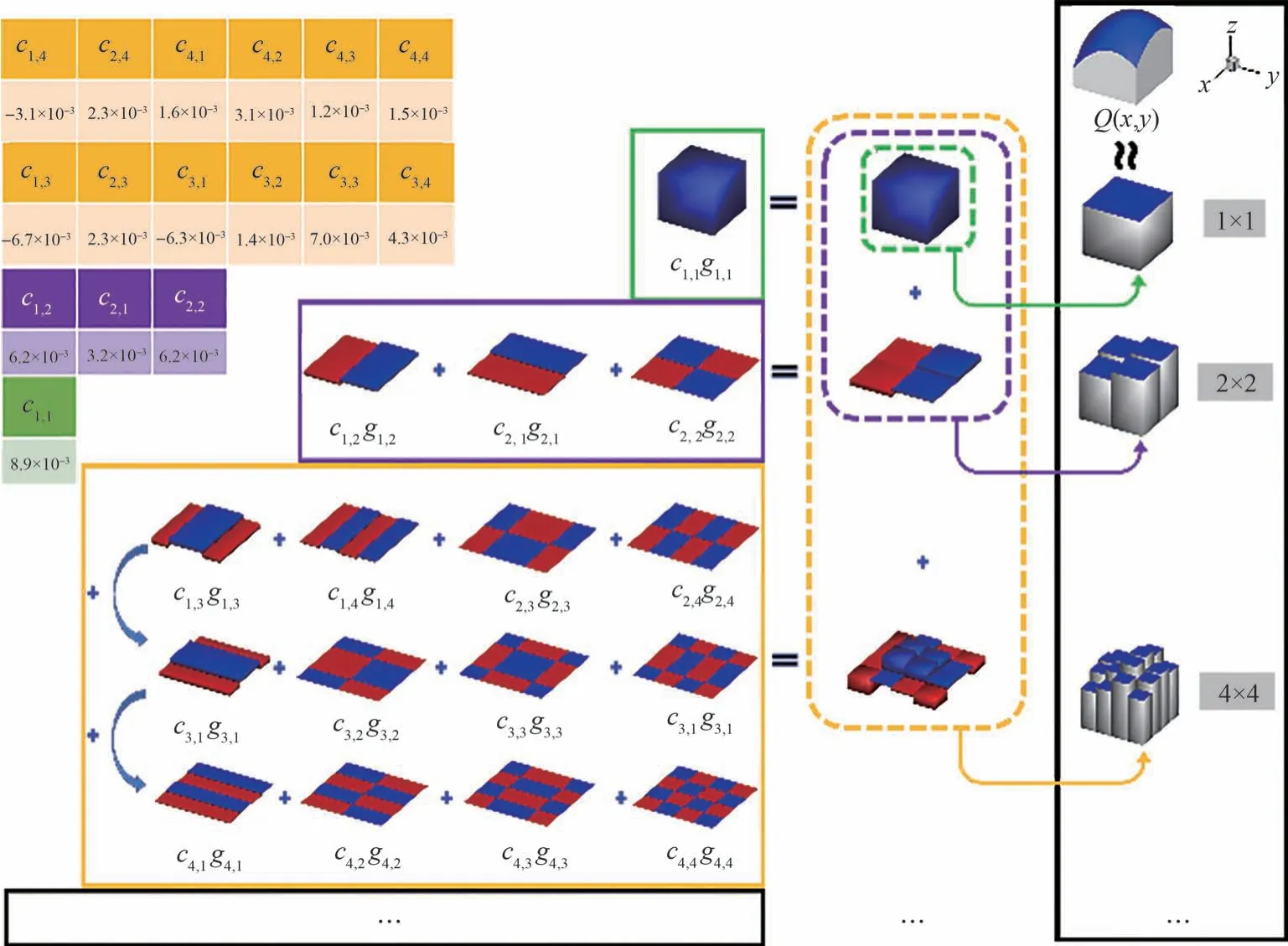
图2 FVM-WBF 方法对单位正方形区域上的变量Q(x,y)=-(x-0.4)2-(y-0.6)2+0.1x sin( 2y )+1拟合数值结果Fig.2 Numerical results of two-dimensional variable Q(x,y)=-(x-0.4)2-(y-0.6)2+0.1x sin( 2y )+1 simulated by FVM-WBF method on unit square area
为直观理解,图2 采用了三维立体的显示视角,从左到右分4 个部分对级数式(2)的数值逼近过程和结果进行展示。第1 部分如图2 左上方所示,给出了3 级基函数(p=0, 1, 2)的拟合系数。第2 部分与第1 部分对应,给出的是3 级基函数与其系数相乘后在单位正方形网格上的取值分布情况。第3 部分如图2 中虚线框标注处所示,分别给出了3 级基函数各级叠加后的结果。可以看到,第1 级基函数在整个网格上形成了常数分布,第2 级基函数在整个网格上形成了2×2 个分片连续的1/2 网格尺度子区域上的离散分布,第3 级基函数则形成4×4 个分片连续的1/4 网格尺度子区域上的离散分布。这表明:第1 级基系数c1,1关联的是整个网格上的变量均值,而第2 级和第3 级基系数分别关联的是1/2 网格尺度和1/4网格尺度的局部区域上的变量均值。图2 的第4 部分从上往下依次列出了变量Q(x,y)在网格内的原始解析分布和利用级数式(2)的近似分布。图中,1×1、2×2 和4×4 分别代表使用第1 级、前2 级和前3 级Walsh 基函数后形成的分片连续区域的数目,可以看到,原始的解析变量在网格内为曲面分布,仅使用第1 级基函数的逼近结果在整个网格上为常数分布,根据g1,1的特征,不难理解系数c1,1即为变量Q(x,y)在整个网格上的均值。在第1 级基函数逼近的基础上,累加第2 级基函数的叠加结果即可获得前2 级基函数的逼近,第2 级系数c1,2,c2,1和c2,2仅在4 个1/2 网格尺度的局部区域上对c1,1代表的均值进行了相应的修正,从而获得了4 个新的子区域上的均值分布。这表明,前2 级基函数级数式是第1 级基函数级数式的直接延伸,并不改变第1 级基函数g1,1对应的系数c1,1。相反,若将延伸部分直接删减,前2 级基函数级数式便可收缩回到第1 级基函数级数式。前2 级基函数级数式对变量逼近表现出的分片连续离散特征和自然“伸缩”数值特性在图2 所示的前3 级基函数级数式的逼近结果中得到了同样的体现。易推断,随着基函数级别的继续增加,这2 种特性将依然得到保持,新增加的一级基函数会比前一级在更小尺度的子区域上对原始均值进行修正,所获得的数值分布也将逐步逼近其解析分布。
前面的描述中,Walsh 基函数是在正方形网格上定义的,对于一般的四边形网格,可通过双线性映射进行网格变换,将二维Walsh 基函数和级数式(2)拓展到任意的四边形网格,得到相应的分片连续区域的离散。图3 取前3 级基函数级数式为例,给出了其在任意四边形网格上形成4×4 个分片连续离散区域的示意,子区域Ωi,j的下标(i,j)由两组对应一维Walsh 基函数级数形成的子区间下标按照张量积顺序给定。
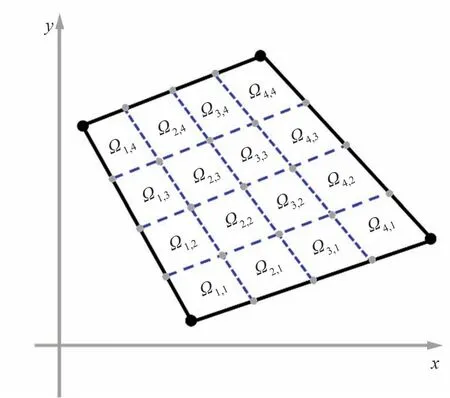
图3 一般四边形网格上的离散子区域示意Fig.3 Subdivision of quadrilateral area
上文分析的级数式(2)所具有的“伸缩”数值特性使得FVM-WBF 方法天然具有便捷的自适应途径,这也是本文自适应方法的理论基础,相关的自适应实现方法将在后面小节进行专门介绍。考虑到方法叙述的连贯性,本节接下来对FVM-WBF 方法的离散求解过程进行描述。
将守恒变量的级数逼近式(2)代入积分控制式(1),可得到关于Walsh 基函数的积分守恒型方程:
该方程包含M×N个待定系数显然,单凭式(6)不能提供足够的定解条件。由于Walsh 基函数的间断性,在控制体内不能保证处处可微,无法利用类似于有限元的变分过程[12,14,17]进行定解。考虑到级数式(2)已经将解变量在控制体Ω上描述成了与待定系数数目相同的分片连续子区域,为了获得满足定解条件的方程数目,选择将式(6)分别在各子区域上进行空间离散,得到关于基系数时间导数的半离散方程:
式中:∂Ωi,j表示子区域Ωi,j的边界为子区域边界处的数值通量,一般采用近似Riemann 求解器或矢通量分裂方法进行计算,和为通过级数式(2)获得的子区域交界面左右两侧的流场守恒变量值;nl和ΔSl分别为子区域交界面处的单位外法线矢量和交界面边长。将控制体Ω内所有子区域上的离散方程联立,可得到矩阵形式描述的常微分方程系统:
式中:
其中:Fi,j表示子区域Ωi,j上的数值通量。采用合适的时间推进格式对方程(8)进行迭代求解,便可得到每个时间步的基函数系数,并由级数式(2)进一步获得各时间步的流动变量值。
2 自适应FVM-WBF 方法
FVM-WBF 方法进行自适应计算的基本过程是先对流场结构进行探测,然后根据探测到的结果对Walsh 基函数数目进行动态配置。下面具体介绍自适应方法使用的流场结构探测器和自适应原理。
2.1 流场结构探测器
流场结构探测器是自适应方法用来对流场结构进行判断和识别的重要工具。借鉴传统的基于流场特征判据[5,7,9]的自适应方法,采用基于流动变量(密度、压强等)梯度构造的探测函数对流场结构进行探测。为了更好地保证计算效率,引入占比因子:
对延伸基函数级数的网格数量MF进行限制,这里M代表计算域内的网格单元总数。从而建立具有双重阈值参数的探测函数:
式中:Qtsd为探测阈值;Qmax为流场中流动变量梯度绝对值的最大值:
式中:∇Qi(1 ≤i≤M)为第i个控制单元上的流动变量梯度,采用Green-Gauss 方法进行计算。
式(10)中的阈值参数ω用以控制自适应“加密”区域的大小,其取值为0 <ω<1。ω取值越接近于1,探测阈值越大,探测到的满足阈值条件的网格数量MF越小,反之MF越大。实际计算中,可根据具体的流场特征对ω进行适当调整,给定具体的值。
式(10)中的阈值参数f(α)由占比因子α确定,用以控制所探测到的需要延伸基函数级数的网格数量不超过给定的百分比α,只有参数ω确定的阈值所探测出的网格占比超过预设值α时才发挥作用,满足0 ≤f(α)<1,可在区间[ω, 1]上由二分法经过若干次迭代后获得,下面给出具体的计算步骤。
步骤 1将区间[ω, 1] 对分得中点f(1)(α)= (ω+1)/2,由f(1)(α)对应的探测函数=f(1)(α)·Qmax获得需延伸基函数级数的网格数量M(1)和占比因子α(1)=M(1)/M。若达到二分结束条件:α(1)=α或|M(1)-MF|≤ℓ,取f(α)=f(1)(α),计算结束。
步骤2将区间[a(1),b(1)] 对分得中点f(2)(α)= (a(1)+b(1))/2,由f(2)(α)对应的探测函数=f(2)(α)·Qmax获得需延伸基函数级数的网格数量M(2)和占比因子α(2)=M(2)/M。若达到二分结束条件:α(2)=α或|M(2)-MF|≤ℓ,取f(α)=f(2)(α),计算结束。
步骤k将区间[a(k-1),b(k-1)]对分得中点f(k)(α)= (a(k-1)+b(k-1))/2,由f(k)(α)对应的探测函数=f(k)(α)·Qmax获得需延伸基函数级数的网格数量M(k)和占比因子α(k)=M(k)/M。若达到二分结束条件:α(k)=α或|M(k)-MF|≤ℓ,取f(α)=f(k)(α),计算结束。
对新获得的区间[a(k),b(k)]重复以上二分操作,直到得到满足结束条件的参数f(α)。以上二分结束条件中的ℓ 是所允许的误差,理想值为ℓ=1,为适当减少二分步数,本文算例中取ℓ=100。
2.2 自适应原理
流场自适应计算一般需要根据流场结构特征,对网格疏密或离散精度的分布进行动态调整。自适应FVM-WBF 方法主要是针对Walsh基函数数目进行动态配置,其自适应的基本原理主要体现在基函数数目的配置和动态调整过程中,接下来将从这2 个方面对FVM-WBF 方法的自适应原理进行描述。
1) Walsh 基函数数目的配置策略
利用探测函数对流场结构进行探测后,将流场识别为流动变量变化剧烈的激波、涡系等局部大梯度区域和流动变量变化相对平缓的光滑区域,即对流场扫描探测过程中,若控制单元内的流动变量梯度∇Qi满足∇Qi≥Qtsd,则识别为大梯度区域,采用Ar1进行标记;相反若∇Qi<Qtsd,则识别为光滑区域,采用Ar2进行标记。自适应FVM-WBF 方法的基本策略是在流场的Ar1区域使用最多数目的Walsh 基函数,而在Ar2区域使用最少数目的Walsh 基函数。实际计算中,该策略将根据不同区域上基函数的级别差异进行适当的修改,其具体的修改原则如下所述:① 当Ar1和Ar2区域上的基函数数目仅相差一个级别时,则保持原始策略不变,即流场仅按Ar1和Ar2这2 个区域进行基函数配置和自适应计算处理;② 当Ar1和Ar2区域上的基函数数目相差超过一个级别时,2 个区域交界面处左右两侧的自由度变化过大,可能给流场求解的稳定性带来不利影响。为避免这一问题,将在Ar1和Ar2区域之间引入若干层的过渡区域,保证相邻区域上的基函数数目不超过一个级别。为描述方便,将过渡区域记为Ar3,该区域使用的基函数数目应介于Ar1和Ar2区域的基函数数目之间。对于这种情形,自适应FVM-WBF 方法将按Ar1、Ar2和Ar3这3 个区域对流场进行基函数的配置和自适应计算处理。
本文的自适应数值计算在流场的Ar1区域内配置p=0, 1, 2 , 3 这4 级Walsh 基函数,其对应的级数式为
在Ar2区域内配置p=0, 1 这2 级Walsh 基函数,对应的级数式为
因Ar1与Ar2区域使用的Walsh 基函数数目相差2 个级别,需要引入过渡层区域Ar3。根据上述基函数配置测率的修改原则,在Ar3区域内配置p=0, 1,2 这3 级Walsh 基函数,相应的级数式为
在数值模拟过程中,流场结构随着时间推进不断演化发展,各个时间步所探测到的Ar1和Ar2区域会随之变动,这样网格单元内的Walsh基函数数目和相应的级数式也会实时进行调整。
2) 网格单元内的Walsh 基函数数目调整
网格单元内Walsh 基函数数目的调整分为2 种情况,一种是延伸基函数的层级,对应基函数数目由少向多的调整;另一种是缩减基函数的层级,对应基函数数目由多向少的调整。根据Walsh 基函数级数式(2)的伸缩数值特性,以上2 种基函数的调整过程仅涉及相关基函数系数的传递和赋值,并不会引入额外的插值或重构计算量,这种Walsh 基函数系数的继承特性对于自适应计算有很大的便利。
而缩减基函数层级的调节情况对应的传递公式为
在后续的自适应流场数值模拟算例中,Walsh 基函数数目的调节对应着级数式(12)~式(14)之间的基系数传递。
3 数值算例
选取双马赫反射问题、Rayleigh-Taylor 不稳定性问题和NACA0012 翼型绕流作为算例,以全局使用2 级、3 级和4 级Walsh 基函数的原始FVM-WBF 方法的计算结果为参照,对自适应FVM-WBF 方法进行性能测试。数值通量计算格式均选用文献[23-25]中的熵相容格式,时间推进选用满足TVD 条件的强稳定3 阶显式Runge-Kutta 方法[26]。在自适应FVM-WBF 方法的计算中,所有算例均采用基于密度梯度的探测函数对流场结构进行识别,级数延伸的网格占比因子α均取为15%。
为方便描述,采用FVM-WBF-ADP 表示自适应FVM-WBF 方法的计算结果,采用FVMWBF-(2,2)、FVM-WBF-(4,4)和FVM-WBF-(8,8)分别表示全局使用2 级、3 级和4 级Walsh基函数的原始FVM-WBF 方法的计算结果,这里(2,2)、(4,4)和(8,8)分别对应2 级、3 级和4 级Walsh 基函数级数式张量积求和的上界。
3.1 双马赫反射问题
双马赫反射问题[27]的流场包含复杂的激波、涡系等结构,经常被用以检验数值方法的精度、分辨率和稳定性等性能。该问题的计算区域为[0,4]×[0,1],描述的是马赫数为10 的正激波沿着放置于(x,y)=(1/6, 0)点处且与x轴成60°夹角的斜坡右行所形成的流场。该流动的初场由激波关系式给定,波前和波后的流动参数分别设置为(ρ,u,v,p)=(1.4, 0, 0, 1.0) 和(ρ,u,v,p)=(8.0, 7.144 71, -4.125, 116.5)。流场区域的左右边界分别按流入和流出边界条件进行设置,上边界为动激波边界,激波前后的参数由激波关系式给定,下边界在x=1/6 的左侧设置为激波后参数,x=1/6 的右侧为无黏壁面条件。
本算例采用了960×240 的笛卡尔网格,计算到t=0.2 时刻。自适应FVM-WBF 方法的计算中,探测器的阈值参数ω设置为0.01。
图4 分别给出了该算例在无量纲时间t=0.05,0.1,0.15,0.2 时刻的密度流场云图(左侧部分)和根据流场探测结果所获得的基函数配置情况(右侧部分)。基函数配置图中的红、蓝、绿部分分别代表使用4 级基函数的Ar1区域、使用2 级基函数的Ar2区域和使用3 级基函数的Ar3过度区域。结果显示,使用到最高级别基函数级数的Ar1区域在各个时刻均与流场中的激波、接触间断和剪切涡等流动结构区域基本一致,说明自适应FVM-WBF 方法能够根据式(10)探测到的流场结构对Walsh 基函数数目进行合理、准确的动态配置。
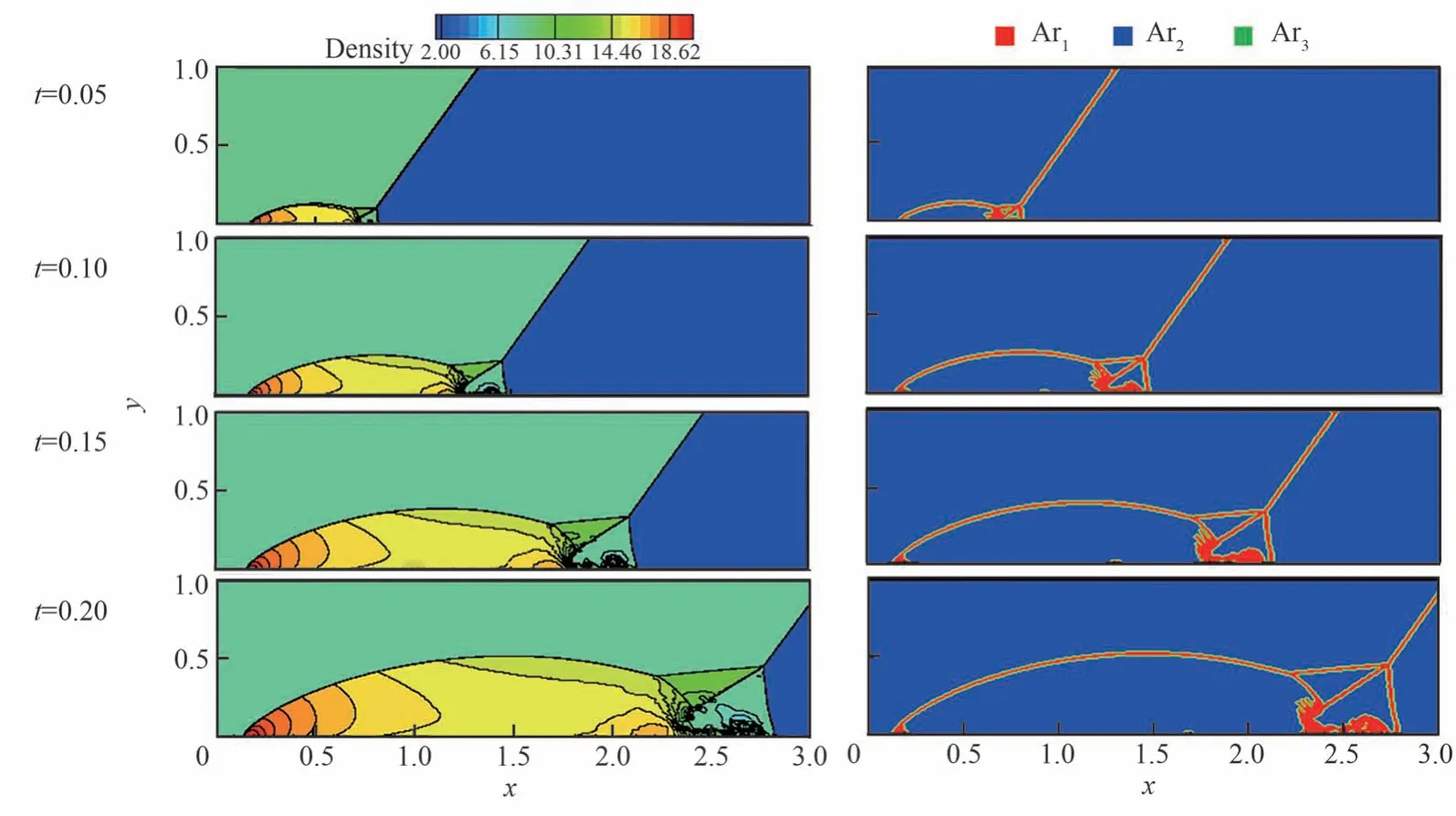
图4 双马赫反射问题在无量纲时间t=0.05,0.10,0.15,0.20 时刻的流场密度云图和对应的Walsh 基函数配置情况Fig.4 Density counters and corresponding Walsh basis function distributions for double Mach reflection problem at time t=0.05, 0.10, 0.15, 0.20
图5 给出了原始FVM-WBF 方法和自适应FVM-WBF 方法在t=0.2 时刻所获得的数值密度云图对比。图中显示,FVM-WBF-ADP 对激波和小尺度涡等结构的分辨率略逊于FVMWBF-(8,8),但明显优于FVM-WBF-(4,4)。表1 进一步比较了4 种计算每100 个时间步所消耗的CPU 时间,可以发现FVM-WBF-ADP 所消耗的CPU 时间分别为FVM-WBF-(4,4)和FVM-WBF-(8,8)的48% 和11%,仅比FVMWBF-(2,2)消耗的CPU 时间多出约48%。图5和表1 中的对比说明:自适应FVM-WBF 方法以略高于FVM-WBF-(2,2)的计算消耗达到了与FVM-WBF-(8,8)相近的分辨率,显示出在平衡分辨率和计算效率方面的优势。
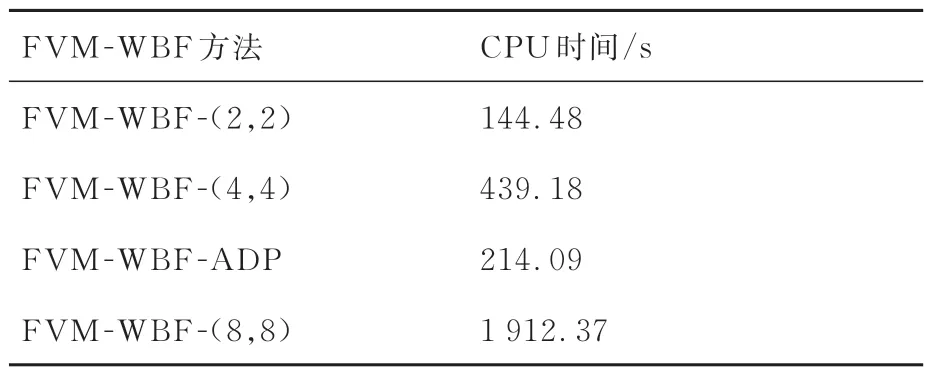
表1 双马赫反射问题每100 个时间步的CPU 时间比较Table 1 Comparison of CPU time per 100 steps for double Mach reflection problem
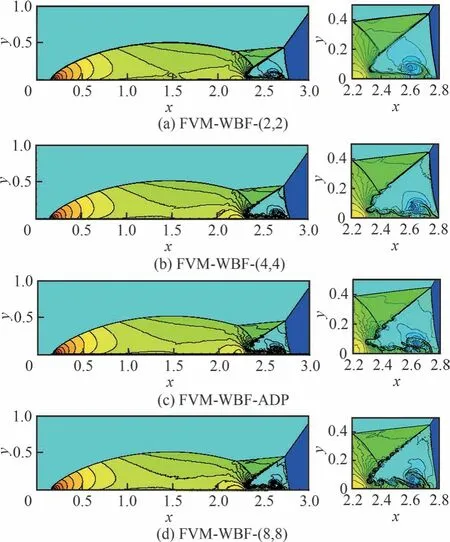
图5 双马赫数反射问题数值密度云图Fig.5 Density counters of Double Mach reflection problem
3.2 Rayleigh-Taylor 不稳定性问题
Rayleigh-Taylor 不稳定性问题[27]也经常被用于检验数值方法的精度和分辨率,其描述的是上下2 层密度不同的流体,当密度大的流体受到重力影响流向密度小的流体时所产生的流动现象。其计算域为[0,0.25]×[0,1],初始条件为
图6 从左到右分别给出了流场在无量纲时间为0.05,1.00,1.50 和1.95 时刻的密度云图(上侧部分)和Walsh 基函数配置情况(下侧部分)。图中显示,随着时间的推进,流场中的结构越来越丰富,各时刻的Ar1区域能够跟随流场结构的演化不断调整和匹配,说明自适应FVM-WBF方法能够通过基函数数目的动态配置实现流场结构的精确捕获。图7 给出了原始FVM-WBF方法和自适应FVM-WBF 方法计算到t=1.95时刻的数值密度云图。在图中可以看到,该时刻的轻流体空泡和重流体“尖顶”相互干扰,形成了多尺度涡的复杂流场结构。FVM-WBF-ADP对多尺度涡的分辨率依然介于FVM-WBF-(8,8)和FVM-WBF-(4,4)之间。

图6 Rayleigh-Taylor 不稳定性问题在无量纲时间t=0.05,1.00,1.50,1.95 时刻的流场密度云图和对应的Walsh 基函数配置情况Fig.6 Density counters and corresponding Walsh basis function distributions for Rayleigh-Taylor instability problem at time t=0.05, 1.00, 1.50,1.95
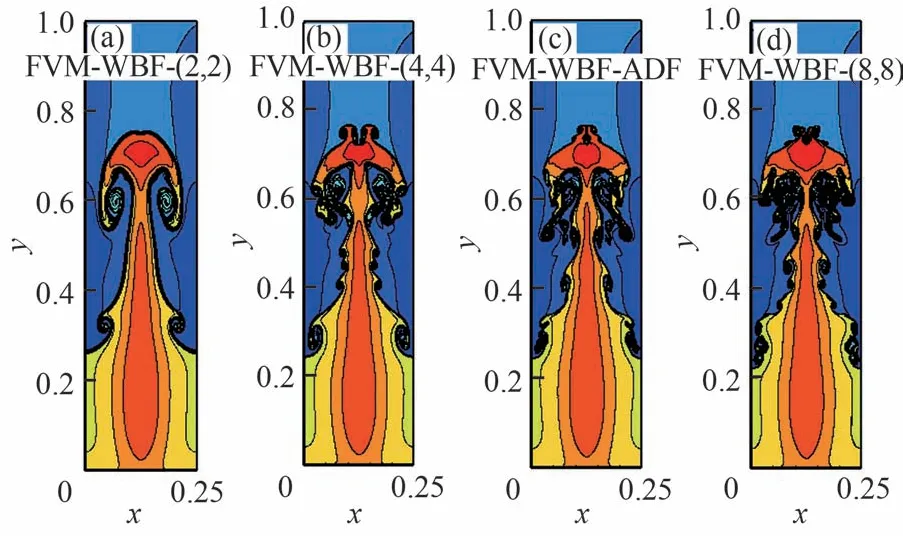
图7 Rayleigh-Taylor 不稳定性问题数值密度云图Fig.7 Density counters of Rayleigh-Taylor instability problem
表2 列出了4 种计算每100 个时间步所消耗的CPU 时间。结果显示:FVM-WBF-ADP 所消耗的CPU 时间分别为FVM-WBF-(4,4)和FVM-WBF-(8,8)的60%和14%。该算例再次表明,自适应FVM-WBF 方法能够在获得高分辨率的同时,实现较高的计算效率。
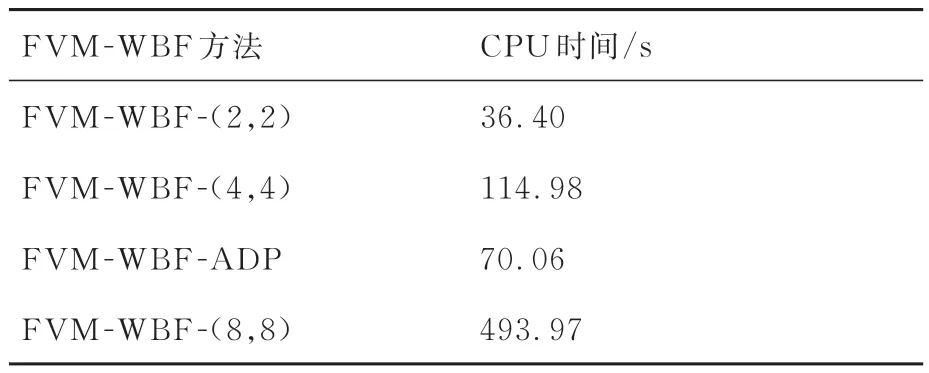
表2 Rayleigh-Taylor 不稳定性问题每100 个时间步的CPU 时间比较Table 2 Comparison of CPU time per 100 steps for Rayleigh-Taylor instability problem
3.3 NACA0012 翼型绕流
以贴近航空工程应用的NACA0012 翼型跨声速定常绕流为例,进一步考察自适应FVMWBF 方法对包含曲面边界和激波的二维复杂流动问题的计算性能。具体计算状态为马赫数Ma=0.8,迎角α=1.25°,网格量为80×40,探测器的阈值参数ω为0.13。
图8 分别给出了流场在时间迭代步数(IT)为1 500、3 000、5 000 和8 000 时的密度云图(上侧部分)和Walsh 基函数配置情况(下侧部分)。结果显示,随着流场的收敛,每个计算网格上的基函数数目的配置也逐渐趋于稳定,Ar1区域所对应的上下翼面激波和前缘位置是流动参数变化相对剧烈的区域,使用了最多数目的基函数。图9 给出的是原始FVM-WBF 方法和自适应FVM-WBF 方法所获得的收敛后的密度云图,图10 比较了计算获得的翼面压力系数分布(选取文献[28]中的3 阶精度结果作为参考)。结果显示,FVM-WBF-ADP 对激波捕捉的锐利程度优于FVM-WBF-(4,4),与FVM-WBF-(8,8)基本相当。图11 比较了残差随无量纲CPU 时间的收敛历程,FVM-WBF-ADP 和FVM-WBF-(2,2)的残差收敛速率几乎完全相同,两者约为FVM-WBF-(4,4)收敛速率的4 倍,约为FVMWBF-(8,8)收敛速率的24 倍。可见,对于翼型绕流这类航空工程中的常规问题,自适应FVMWBF 方法同样具备兼顾高分辨率和高计算效率的良好性能。
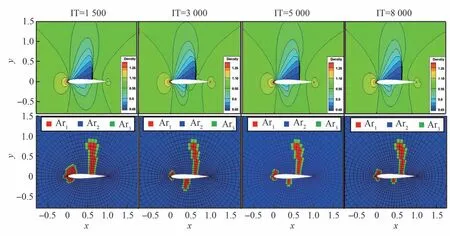
图8 NACA0012 翼型绕流在迭代步IT=1 500,3 000,5 000,8 000 时的流场密度云图和对应的Walsh 基函数配置情况Fig.8 Density counters and corresponding Walsh basis function distributions for the flow over NACA0012 airfoil at iterative step IT=1 500, 3 000, 5 000, 8 000
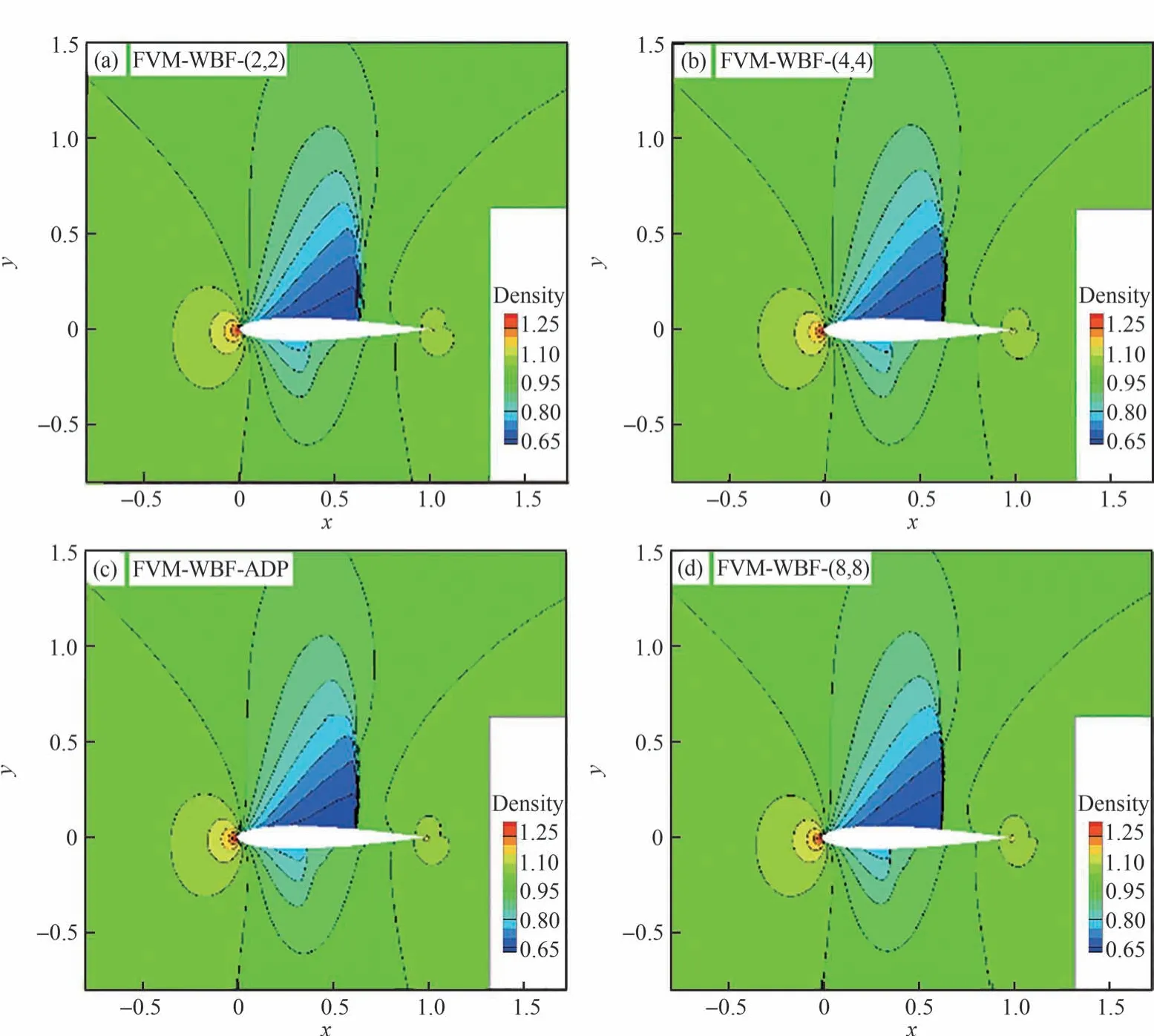
图9 NACA0012 翼型绕流数值密度云图Fig.9 Density counters of flow over NACA0012 airfoil
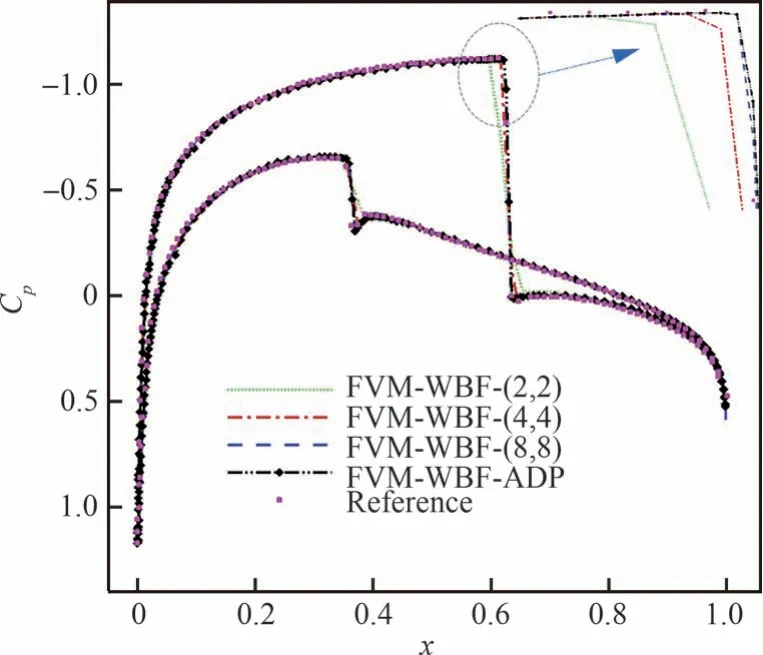
图10 翼面压力系数分布比较Fig.10 Comparison of pressure coefficient distributions
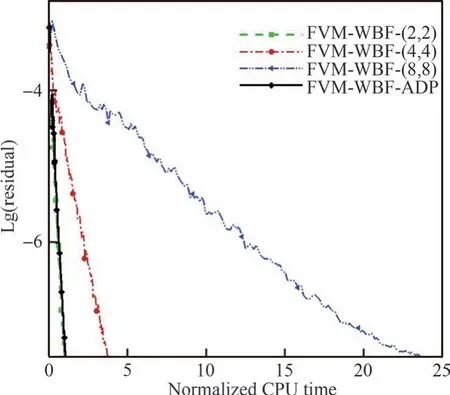
图11 残差收敛历程比较Fig.11 Comparison of residual convergence histories
4 结 论
利用Walsh 基函数的数值特性,发展了一种对基函数数目进行动态配置和调节的自适应FVM-WBF 方法。采用若干数值算例,对该方法的分辨率和计算效率进行了测试和验证。在自适应计算过程中,该方法表现出如下特点和优势:
1)自适应FVM-WBF 方法能根据流场结构,动态增减和配置各个网格单元上的Walsh 基函数数目,仅在流动变量变化剧烈的局部区域配置足量的Walsh 基函数,从而有效避免了计算量的爆发式增长。
2)利用Walsh 基函数级数“伸缩”前后重叠项系数的继承性,自适应FVM-WBF 方法根据流场结构增减网格单元内的基函数数目时,仅涉及基函数系数的传递,不必引入额外的插值/重构计算,具有灵活方便和计算量小的优势。
综上所述,FVM-WBF 方法具备天然、便捷的自适应潜能,能够通过对Walsh 基函数数目的自适应配置和动态调节达到对高分辨率和高计算效率平衡和兼顾的效果。
本文的自适应工作主要针对结构网格上的无黏流动,后续工作中将继续发展非结构网格上的FVM-WBF 方法,并将该方法推广至黏性流动问题的求解。
