基于量子测量的量子计算模型综述

2023-06-26郑星舟罗明星

重庆邮电大学学报(自然科学版) 2023年3期

郑星舟,罗明星

(西南交通大学信息科学与技术学院,成都 610031)

0 引言

量子计算机是基于量子叠加原理和量子演化建立的特殊计算模型。量子态具有叠加性,可以并行表示信息,因此,量子计算机具有并行处理问题的能力,针对某些问题如大整数分解可以提供比经典计算机更高效的计算能力[1]。最近十年,量子计算机在产业化方面得到非常快速的发展,霍尼韦尔、谷歌、IBM、国盾等企业已经建立了上百量子位的量子计算机原型。量子计算技术的工业化已日趋成熟,在未来5—10年将实现中等规模的量子产业链,并对网络空间安全、金融安全、化学制药、国防安全、量子物理模拟等方面产生深远影响[2-3]。

与经典图灵机模型基于经典逻辑门类似,量子计算基于量子逻辑门构建量子线路模型。首先,选择简单的初始化,如逻辑0态;然后,针对特定任务设计全局量子演化线路,并利用通有的小规模量子模拟系统,如单量子位门或两量子位门,分解全局量子演化,得到基于小量子逻辑门的量子线路,完成量子态的演化;最后,利用量子测量读取信息。这种标准的量子线路模型,便于大规模集成和工业设计,但是其线路设计的复杂度非常高,一般都是指数量级,这也是量子线路模拟的局限。

此外,利用量子系统的物理演化也可以构造量子计算模型,即针对特定计算任务构造量子系统的哈密尔顿系统,并通过系统的绝热演化来求解问题[3-5]。这种物理演化不需要设计量子线路,但是需要针对大规模量子系统的物理控制,具有非常大的实验难度,目前的量子控制技术还无法支持大规模物理实验。量子线路模型和绝热演化模型是等价的,都依赖于量子系统演化的酉(Unitary)不变性。

与这两个模型不同,文献[6]提出基于局部量子测量和经典通信辅助的单向量子计算模型。这种新的量子计算模型利用特定的量子纠缠态,基于局部测量来完成量子计算任务。他们引入量子纠缠簇态作为量子计算资源,并在理论上证明通过只对个别量子位执行局部测量就能实现一般的量子线路。单向量子计算是通用的量子计算模型。这种量子计算模型便于物理实现。针对多目标的单向量子计算也有很多研究成果,包括其纠缠特征的量化,量子资源态的研究,量子计算任务的设计等。文献[7]提出新的框架来刻画在一维空间上基于局部测量的量子计算对近距离纠缠对称态的处理能力。由于基于二维量子位(量子比特)的单向量子计算只能验证2n-1个量子比特的布尔函数,文献[8]拓展相关结论,构造了基于三维量子位的单向量子计算模型,并利用广义GHZ(Greenberger-Home-Zeilinger)态为资源,实现最多使用3n-1个量子位的布尔函数。文献[9]优化了量子计算资源,包括可用量子操作以及可访问的量子位数目,并验证可在非适应性的单向量子上计算的布尔函数。对于受限于稳定子理论的非适应性单向量子计算,他们给出了计算给定布尔函数所需要的最少量子位。文献[10]基于信息流引入单向量子计算模型,并给出多项式时间复杂度算法找到最优的信息流演化过程。文献[11]在非马尔可夫环境下研究了单向量子计算的精确开放系统动力学,以及平均精度与基于泡利X门和Z门的局部观测的关系。文献[12]证明双酉量子线路可以为扩展单向量子计算提供理想的框架,并将双酉量子线路应用于量子多体系统,有效地实现了空间方向上的量子计算。

针对量子逻辑门的并行化问题,文献[13]发展基于多量子位超图态的联合受控技术,引入广义单向量子计算框架,并平衡计算时间和空间复杂度。由于计算中会产生量子噪声,文献[14]提出容错的单向量子计算模型,将任意有稳定子码的容错量子计算方案映射到基于局部测量的单向量子计算框架。此外,也有一些研究单向量子计算与时间序列起源、计算复杂度,以及经典的自旋模型的关系。

单向量子计算也可以用于构建量子云系统。任意经典的客户端可以将其计算任务委托给具有较强量子计算能力的量子工厂。其核心思想就是利用砖形量子逻辑线路和随机信息隐藏在保证计算正确性的基础上,保护计算任务的隐私性[15]。

文献[16]设计了一个基于单向量子计算设计原理的软件包Q2Graph,用于设计和测试量子计算算法的简单图。文献[17]将其与applet上的七色板谜题相互关联,用于推广单向量子计算。目前,已有多个实验团队通过不同的物理系统,譬如光学、冷原子、原子系综等实现纠缠簇态的制备和操作,这为单向量子计算技术的发展提供了良好的技术支持[18]。本文主要给出单向量子计算的基础模型,总结其潜在问题和前沿研究方向,为研究者提供借鉴。

1 量子计算

1.1 量子计算起源

量子计算这一概念可以追溯至19世纪80年代[19]。1981年,文献[20]提出利用量子系统模拟物理现象,而使用经典计算机不可能有效地模拟量子系统。随后,研究者们提出基于量子力学的图灵机计算模型,通过使用一个可控的量子系统去模拟另一个量子系统。文献[21]提出快速量子傅里叶分解算法,并证明量子计算机能以多项式复杂度完成大整数的分解。目前最好的经典算法需要亚指数复杂度。譬如,经典计算机分解1个300位整数会消耗三分之一宇宙年龄,而量子计算机只需要10分钟。在过去几十年里,量子实验技术取得了很大的进展,虽然目前还没有建立大规模的量子计算机,但量子计算已经对经典密码学,特别是基于大数分解的公钥密钥系统的安全产生影响。现有的绝大多数公钥密码算法如RSA、Diffie-Hellman、椭圆曲线等都有可能被量子计算机攻破,因此,研究者提出了可以抵抗量子计算攻击的密码算法,称为后量子密码。目前,量子计算、量子通信、量子信息等方向已经发展成为新的交叉学科,即量子信息科学。

1.2 量子线路模型

量子计算是基于量子力学原理构建的计算模型,如图1所示。

图1 Bloch球Fig.1 Bloch ball

从信息科学的角度,量子力学包括如下3个重要的原理。

1)叠加原理。任意孤立的量子纯态(Pure state)可以表示为复内积空间中的单位向量。与经典计算机的0和1两个比特表示不同,量子纯态可以是单位圆周上的任意单位向量,因而提供了超越经典计算机的信息表示和存储能力。从物理系统角度,叠加是一个波的形式,不同的量子态可以进行加法运算。对于具有两个维度的量子纯态,可以表示为一个2维单位向量,也称为量子比特,即|φ〉=α|0〉+β|1〉,其中α和β是两个任意复数,满足|α|2+|β|2=1,见图1a。

2)量子纯态的酉演化。在量子力学中,量子态的演化服从薛定谔演化方程[22]。对于孤立的量子系统,量子纯态的演化等价于复空间上的矩阵变换。一般地,量子演化等价于将特定的酉矩阵应用于量子纯态的表示向量上。一些基本的小规模量子系统的演化矩阵称为量子逻辑门。例如,量子比特翻转门(即经典的NOT门,或者泡利X门),其矩阵表示为

(1)

它将Bloch球上指向北极的单位向量|0〉翻转至指向南极|1〉,反之亦然。另一个例子是Hadamard门,其矩阵表示为

(2)

(3)

对于多量子比特系统,也可以定义量子纯态的演化矩阵。譬如,2个量子比特的受控相位翻转,第一个量子位是控制位,第二个是目标量子位,其量子运算定义为

CZ|i〉|j〉=(-1)ij|i〉|j〉

(4)

它利用控制位的状态|1〉来控制目标位|1〉的相位翻转。另一个类似的例子是2个量子比特的受控比特翻转,其量子运算定义为

CX|i〉|j〉=|i〉|i⊕j〉

(5)

利用控制位的状态1来控制目标位的比特翻转。这些单量子比特逻辑门和两量子比特逻辑门可以用来模拟任意多比特的量子逻辑门,也称为通用量子逻辑门。

3)量子测量。与量子系统演化不同,对量子纯态的测量一般得到随机的输出,其输出概率分布取决于量子纯态的形式和测量坐标系。在量子力学中,任何可观测的物理量都可表示为厄密矩阵表示,其特征值是实数。可观测量的物理实现是将被观测量子系统投影到其特征向量上,而观测结果就是该特征向量所对应的特征值。经典物理的观测对应于相互正交的投影测量。量子测量可以表示为更一般的正算子测量,其矩阵表示为正的半定算子。量子测量输出的概率分布遵守伯恩规则。例如,对单量子比特态|φ〉=α|0〉+β|1〉进行投影测量,其输出0和1的概率分别为

p[0]=〈φ|0〉〈0|φ〉=α2

(6)

p[1]=〈φ|1〉〈1|φ〉=β2

(7)

通常,得到某一输出的概率是被观测量子态与该输出相关的特征态的系数的模平方[22]。

如果有N个量子比特,则共有2N个正交的基态(从|0,…,0〉到|1,…,1〉)。一般的N个量子比特态可以表示为

(8)

它是一个2N维复空间中的单位向量,包括指数数量的系数。量子电路示意图如图2所示。

图2 量子电路Fig.2 Quantum circuit

从量子实验角度,要实现N量子比特系统的整体控制和演化非常困难,这也是经典计算机无法完成物理系统演化模拟的主要原因。为此,研究者将其分解为更小的可控制的量子逻辑门,譬如单量子比特逻辑门和两量子CX,见图2a。

在经典计算机中,与、或、非门的集合是普适性的,可以用来构造任意经典计算线路。与此类似,在量子计算中,也存在这样的普适逻辑门。事实上,任何多量子比特的酉矩阵都可以分解为单量子比特和两量子比特逻辑门的序列[23],其中,单量子比特门执行局部旋转,而两量子比特逻辑门实现量子关联,即量子纠缠。譬如,考虑两量子比特Bell态如

(9)

此联合系统无法表示为2个孤立的单粒子系统,且2个量子比特随时处在相同的状态。一般地,可以利用单量子位泡利矩阵表示4个两粒子Bell态,即

(10)

(11)

(12)

(13)

(14)

GHZ态是三量子比特纠缠态,不能分解为两量子比特与单量子比特态的张量。

1.3 重要量子态

1)图态。图态是重要的量子资源。量子位在图的顶点。图态可以用一个量子演化过程来定义：所有量子位的初始化态为|+〉,相邻两个量子位之间可以定义类似Ising的相互作用,并利用CZ逻辑门实现一对相邻量子位的关联操作,即

(15)

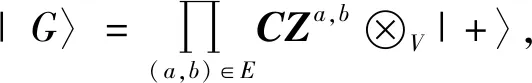
2)簇态。与一般的量子图态不同,簇态要求底层图是正则图,即每个顶点具有相同数量的邻点。低维簇态包括一维晶格或二维正方形晶格,如图3所示。

图3 簇态示意图Fig.3 Schematic diagram of cluster state

考虑一个d维的晶格,在位置a处的系统关联哈密顿量定义为

(16)

它等价于低温量子Ising模型,其哈密顿量为

HIsing=-g(t)∑a,a′f(a-a′)ZaZa′

(17)

簇态是正则图上的一种特殊图态,也是通有的量子计算资源,可以用来构建针对一般量子计算任务的单向量子计算模型。

3)矩阵乘积态。矩阵乘积态是一种特殊量子态,在基态时表示系数可以通过矩阵乘积来计算。矩阵乘积态的思想来源于密度矩阵重整化群。由于基态的参数存储复杂度随量子个数N的增加呈指数上升,经典计算机无法严格对角化来求解基态。但是,可以将整体态表示为基态上的系数张量。例如,一维晶格上的量子态可以表示为

A[N]sN)|s1,…,sN〉

(18)

(18)式中：A[i]si表示关于位置i量子态si的矩阵表示;d表示物理系统的维数。3阶张量如图4所示。

图4 3阶张量示意图Fig.4 Schematic diagram of the third order tensor

(19)

直积态可以表示为

|00…0〉k+1⊗…⊗|00…0〉N

(20)

其中

A[i]0=1,A[i]1=0(i≠k),

(21)

对于N维GHZ态,其量子态表示为|0〉⊗N+|1〉⊗N,其矩阵乘积态系数表示为

(22)

矩阵乘积态为低维量子基态问题提供了高效的计算方法,可以大大降低计算复杂度。矩阵乘积态具有以下性质：①任意将系统分为左右两部分,基于纠缠度量可以计算一维带能隙系统基态的性质;②矩阵乘积态对应的二阶关联函数随着距离指数下降。这也是一维带能隙系统基态的性质。在严格对角化过程中,量子纯态的参数个数随N呈指数增加。但在矩阵乘积态中,给定辅助指标的截断维数,其包含的参数个数随N仅呈线性增加。事实上,如果将多量子比特态表示为N个二阶或三阶张量构成的矩阵乘积形式,可以将求解基态问题转换为张量的最优化问题,表示为

Emin=minφTr(H|φ〉〈φ|)

(23)

对于一般高维矩阵乘积态而言,虽然张量的计算复杂度非常低,但其存储具有指数复杂度。

4)投影纠缠对态。投影纠缠对态是可以用局部量子位到局部物理自由度的投影来描述的量子态。矩阵乘积态是特殊的投影纠缠对态。利用无限长度的投影纠缠对态可以模拟近邻或次近邻相互作用的、正方形晶格上的二维量子模型。与密度矩阵重整化群及量子Monte-Carlo方法相比,投影纠缠对态可以表示纠缠面积定律,也可以用于研究Fermionic模型,Hubbard模型等。

5)张量网络态(Tensor network states)。张量网络态是一种特殊的量子态。在张量网络表示中,高阶张量可以表示为多个低阶张量缩并的形式。一般地,n阶张量用n个指标表示,任意2个张量的指标缩并对应于相同指标的链接。局域张量与投影对纠缠态的投影有关,如图5所示。

图5 张量网络与隐形传态示意图Fig.5 Schematic diagram of tensor networks and teleportation

图5考虑局域相互作用的多量子系统,由于粒子数很多,其张量阶数也很高,相应的低阶张量也多,图形是一种很好的表达形式。张量网络态适用于描述量子多体系统基态的特定纠缠结构,即通过小张量缩并得到的量子态能精确表示多体系统的基态和低激发态。这样极大地减小了数值复杂度。譬如,一维带能隙态对应于矩阵乘积态;二维带能隙态(包括有拓扑序)对应于投影纠缠对态。张量网络态表示也被应用到其他领域,如统计物理、量子化学、机器学习等。张量网络态是一种普适的量子态表示方法,可以表示一般的量子态。各种量子资源态对比如表1所示。

表1 各种量子资源态的对比Tab.1 Comparison of different states

6)贝尔态测量。也称作贝尔基测量,对应于对两个量子位的联合测量,其测量表示见(10)—(13)式,测量的结果是将两个量子位投射到4个贝尔态{|Bij〉}中的任何一个。两量子态的联合测量在实验执行上具有一定难度,可以通过先执行两量子变换,再执行量子投影测量。

2 基于测量的量子计算

基于测量的量子计算利用量子纠缠资源、单量子位测量和经典通信辅助来完成量子计算任务,目前,已经拓展到基于量子隐形传态、状态转移和相关空间的量子计算模型。这些方法为发展基于单向模型的量子计算提供了新的研究方法。

2.1 单向量子计算与簇态

单向量子计算是基于量子簇态构建的量子计算模型。单量子位测量只能减少多量子系统的纠缠量,因此,量子簇态中量子测量的计算是单向的。标准量子线路模型的量子电路可以转换成簇态的测量。利用不同的测量基和测量线路可以改变量子计算的线路。在单向量子测量过程中,量子纠缠作为量子资源被消耗,具体来讲,在局部位的量子测量中,泡利矩阵和单量子比特旋转门的演化满足

Rx(θ)X=XRx(θ)

(24)

Rz(θ)X=XRz(-θ)

(25)

Rx(θ)Z=ZRx(-θ)

(26)

Rz(θ)Z=ZRz(θ)

(27)

(24)—(27)式中：Rx(θ)表示沿泡利x轴旋转θ;Rz(θ)表示沿泡利z轴旋转θ。一般地,可以得到

UX=X(XUX)

(28)

UZ=Z(ZUZ)

(29)

(28)—(29)式中：X,Z为泡立矩阵;U为单粒子旋转变换。利用单粒子测量,可以得到

Rz((-1)bβ)ZaXbRx(α)|ψ〉=

ZaXbRz(β)Rx(α)|ψ〉

(30)

两粒子的演化方式为

CZ(Z⊗I)=(Z⊗I)CZ

(31)

CZ(X⊗I)=(X⊗Z)CZ

(32)

(31)—(32)式中,CZ为受控非门。

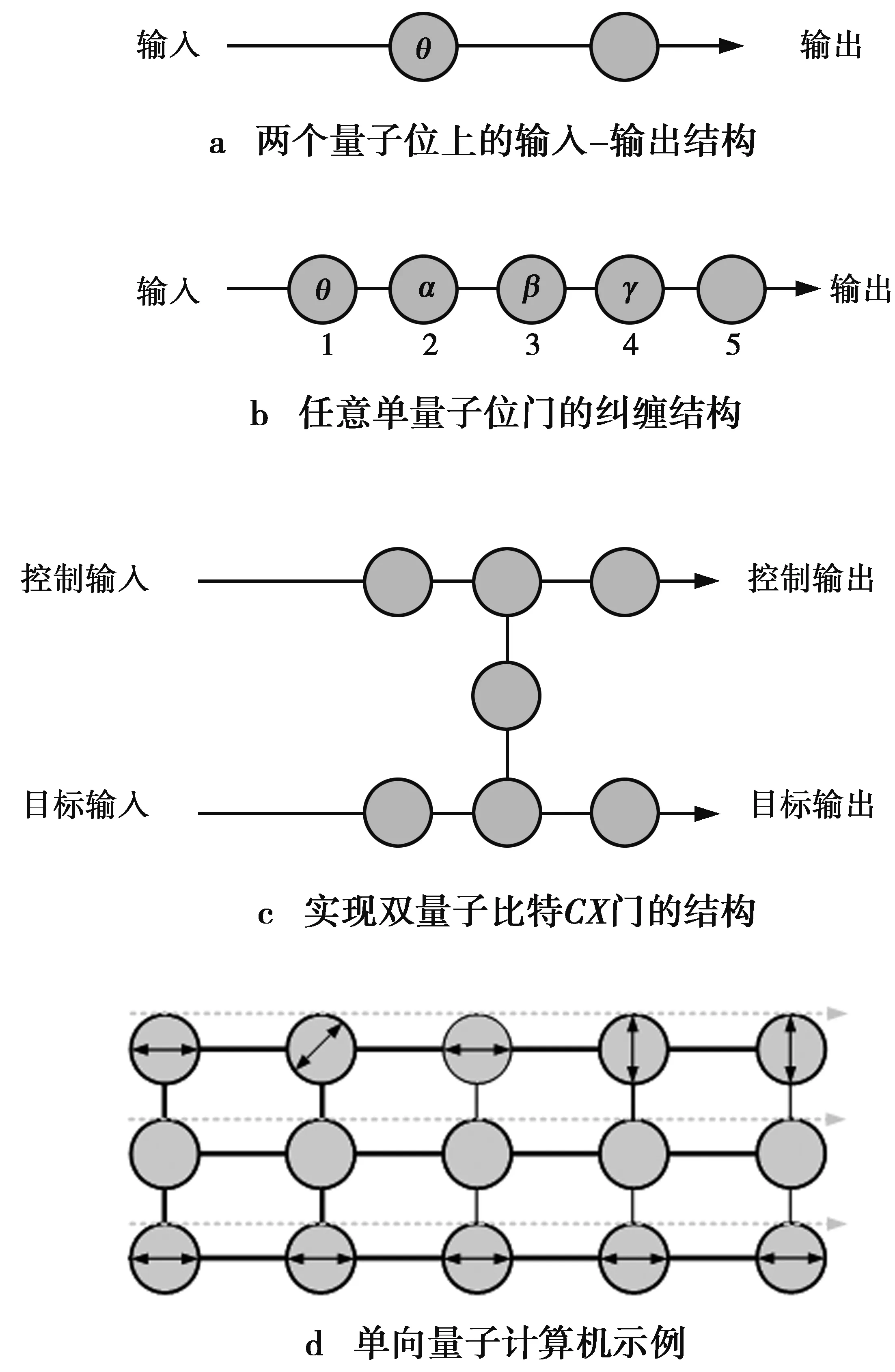
图6 单项量子计算机的通用门实现Fig.6 Universal gate implementation of one-way quantum computing model

与任意的单量子逻辑门相比,测量轴的适配性并不是实现两量子比特受控非门的必要条件。基于二维晶格模型,利用局部测量也可以实现任何的量子电路。因此,二维簇态也是量子计算的通用资源。这种计算模型的优势主要在于其通用性,原则上可以处理所有问题。在实际应用中,这种模型也存在缺点,譬如量子簇态的设计和制备、量子局部关联的演化和测量误差的传递问题等。考虑到这些问题,基于簇态的单向量子计算模型比较适合于小规模的量子计算和量子系统模拟。

2.2 基于隐形传态的单向量子计算模型

基于测量的隐形传态量子计算如图7所示。基于量子纠缠,文献[24-25]基于量子隐形传态构造一种量子计算模型,其基本原理见图7a。引入单量子比特旋转基B：={|BU〉cd},量子隐形传态的理论依据为

图7 基于测量的隐形传态量子计算Fig.7 Measurement based quantum computation of teleportation

(33)

|Bcd〉=ZcXd⊗I|B00〉

(34)

基于共享的纠缠对|B00〉(4个贝尔状态之一),或者其他量子纠缠态作为量子信道,信息传递方对信道上的粒子和输入的未知粒子作两粒子的贝尔联合测量,并将测量结果编码为两比特经典信息cd,发送给接收方。接收方基于经典的测量结果cd利用单量子比特操作ZcXd可以恢复出传输的未知量子比特。基于隐形传态[24-26],利用局部测量和分布式量子纠缠资源就可以执行一般的量子计算。这种计算模型的主要原理是基于纠缠信道实现量子态和单量子比特旋转,见图7b。

另一方面,利用两量子比特逻辑门U可以旋转2对贝尔态的4量子位态,实现两量子位门的远程变换,见图7c。利用4量子比特的联合测量,可以远程执行两量子比特逻辑门,如CX门。单量子逻辑门和两量子CX门是普适的,图7提供了一个通用的量子计算模型。

基于隐形传态的量子计算模型不依赖于量子资源态,如簇态。因此,可以将所有量子位设置为固定的|0〉状态。量子纠缠可以通过纠缠交换来实现。与单向量子计算机的单个量子位测量不同,本模型需要联合多量子位的测量,是单向量子计算模型的拓展[6,27]。由于联合测量在实验上较难,有研究者提出减少联合测量的量子位数[28-29]。最近,研究者证明两个模型是等价的[30]。进而,文献[31]将两个模型统一起来,如图8所示。

图8 量子逻辑门的远程执行Fig.8 Remote implementation of quantum gates

2.3 基于量子态转移的量子计算方案

Perdrix基于量子态的转移提出一种单向量子计算模型[32],其主要思想是利用单量子位和双量子位操作,如图9所示。

图9 基于状态转移实现单向量子计算Fig.9 One way quantum computation via state transition

假设所有观察值都有0、1(或者+1、-1)2个结果,其基本的状态转移见图9a。图9a中,每个方框表示一个可观察对象,代表投射到其可观察特征态的+1或-1子空间上的2个测量结果。与隐形传态不同,量子态转移只使用2个量子比特来传输1个量子比特。事实上,任意的单量子比特门可以通过旋转量子态转移中的可观察对象来实现,见图9b。通过辅助量子位和投影测量相结合可以实现两量子CX门,见图9c。利用这种量子态转移,可以在一维簇态下将单向量子计算和基于隐形传态的量子计算联系起来[33]。在量子态传输和隐形传态模型中,可以通过两量子位测量来实现量子计算的普适性。因而也可以研究两量子位联合测量的模拟实验难度[29,31]。除了量子计算的量子态转移,还可以构造基于测量的量子图灵机模型[34]。与基于量子隐形传态的计算模型相似,这种量子态转移计算模型也不依赖于量子簇态资源,便于量子任务的构造,是普适的量子计算模型。但是,这需要考虑两粒子的联合测量,以及一般的酉变换,其实验难度较大。基于量子态传输和隐形传态模型的量子计算模型比较适合于分布式的环境,可以构造量子云计算,或者量子代理计算模型。

2.4 张量网络

文献[35]使用Valence-Bond态图来构造单向量子计算模型,利用Valence-Bond张量网络来解释量子簇态,也称为投影对纠缠态。除边界外,每个图的顶点有4个虚拟的量子位,2个相邻的虚拟量子位形成最大量子纠缠对,或者一种Bond。由于每个点也都是一个量子位,因此,通过|0000〉→|0〉和|1111〉→|1〉,即重复编码,将4个虚拟量子位映射到1个物理量子位。除重复编码外,一般的投影对纠缠态需要更一般的局部映射。量子计算在虚拟量子位上执行[25,27]。随后,文献[36]提出相关空间的单向量子计算,利用量子态的张量网络结构,例如一维矩阵积态[37]以及二维投影纠缠对态[35,38]来实现量子计算任务。

基于张量网络的量子计算模型可以快速求解一些特定的物理问题,譬如低维晶格上的量子基态,以及低激发态的量子纠缠;也可以应用于解决一些量子态模拟问题,譬如量子化学、凝聚态物理等。张量网络是一种构造单向量子计算的方式,其局部张量的缩并是加快量子计算的关键,也是其应用的局限。针对特定的问题,需要考虑量子张量态的快速表示,这是张量网络应用的另一个瓶颈。各种量子计算模型的性能对比如表2所示。一方面,大部分量子计算模型都是普适的,可以用来构造一般的量子计算机;另一方面,这些普适模型存在相应的缺点,对一般问题的加速能力有限,这也是量子计算的主要问题。因此,单向量子计算的发展方向与其他量子计算模型一样,都应该聚焦在特定应用场景。此外,考虑到这些模型的特点,可以尝试设计各种特定的应用模型。

表2 各种量子计算模型对比Tab.2 Comparison of different quantum computation models

3 基于测量的量子计算实验进展

基于测量的量子计算模型,特别是基于光子、离子阱、超导、量子点等物理模型构建的量子计算模型在物理实验上也取得了很多进展。光量子态作为现代量子通信的主要载体,被广泛应用于量子计算模型[38]。2001年,文献[39]首先实现了线性光学的量子计算。2005年,文献[40]利用线性光学实现基于隐形传态的计算模型中的受控逻辑门。文献[41]等制备4光子簇态并实现一些基本的逻辑门,以及简单的Grover算法。对于一般的图态,光子的多自由可以用来构造高维量子系统[42]。文献[43]基于多自由光子和纠缠态来实现传输量子门的实验方案。文献[44-45]利用连续变量实现单向量子计算。通过辅助前馈技术降低测量随机误差,从而可以完成近似确定的单向量子计算逻辑门[46-47]。基于单向量子模型可以模拟各种常见的算法[48-51]。目前,光学模拟系统的主要挑战在于构造高保真逻辑门和控制错误概率等方面。

基于离子阱的系统将离子囚禁在二维阱中,利用其冷却后的能级编码量子态。通过调整阱的几何结构可以用来制备低维簇态[52-53],模拟逻辑门操作[54]。这种技术可以用来实现长时间的相干和信息存储[55-57]。另一种方案是基于超导量子系统,基于超导约瑟夫森结编码,通过调控电流、电场或微波实现量子门操作。超导量子电路可以制备大规模簇态[58]。光子、离子阱和超导量子技术发展非常迅速,具有优势,不过,没有哪种技术具备量子计算机的所有优点,还需要克服各个模拟系统的技术屏障,为真正实现量子计算提供支撑。

4 量子纠缠资源

在基于测量的计算中,算法的量子部分是在量子资源态中进行的局部量子测量,而其他经典信息对应于量子测量的选择以及对测量结果的后验处理。其具体形式可以概括为2种：①允许(自适应选择)局部量子变换以及局部量子测量;②允许量子层只有深度1,而经典层可以有任何深度。在这种形式中,任何单向量子计算都可以看作是经典和量子层的交互序列。总的量子态从一个量子层传递到下一个量子层,下一层中进行的量子作用由前一层量子测量结果的经典计算来确定。因此,任何多项式时间复杂的量子计算都可以用多项式数量的量子层来实现。但是,一般地,任何多项式时间复杂的量子算法需要多少量子层并无从知晓。