图形运动学习中直观想象的运用

于飞 何优优

摘 要：直观想象是学习图形运动内容的重要方式。图形运动学习中直观想象的运用，可以借助变化与比较的策略，具体包括在关注轨迹中聚焦变化过程、在比较异同中建立数学模型两个层次。由此，在六年级设计和实施《图形的运动》综合练习课，引导学生想象运动轨迹，系统感受图形运动的变化规律；比较变化要素，切实体会图形运动的模型价值。

关键词：小学数学；直观想象；图形运动；综合练习

一、直观想象与图形运动的学习

作为直观想象的重要载体，图形是数学研究的基本对象之一。运动变换是研究图形的重要视角，有助于整体认识图形，比较把握图形要素之间的关系。图形的运动是小学数学的重要内容，涉及平移、旋转、轴对称等刚体运动以及放大、缩小等形变运动。

不同的运动因为关注不同的要素，呈现出各自的特点。比如，平移运动关注平移方向和平移距离等，旋转运动关注旋转中心、旋转方向和旋转角度等，而轴对称运动实际上是（图形）在空间中绕轴（线）旋转180°。图形运动的学习，不能只关注运动的结果，而需要更多关注运动的过程。静止的图形比较容易通过直观来认识，而运动的图形更需要通过想象运动的过程，把握运动的结果。因此，直观想象是学习图形运动内容的重要方式，也是要培养的重要核心素养。特别是面对复杂的图形运动，想象运动过程和把握运动结果更需要较强的直观想象能力。

二、策略要义

首先是变化。变化指物体运动的情况，更加聚焦运动的过程。在图形运动中指运动从开始到结束的整个过程，包括运动轨迹所形成的新圖形等。对运动过程的感受与体验有助于打开想象空间，培养直观想象能力。其次是比较。比较指对比事物的相同与差异，从而明晰事物的本质，加深理解。图形经过运动就有变化，由此便可比较，从而把握“变”与“不变”的规律，发展直观理解能力与空间想象能力。变化与比较作为一种策略，具体包括两个层次：

一是在关注轨迹中聚焦变化过程。运动轨迹其实是运动过程的显性化描述。图形运动知识的学习，从原先仅关注运动的结果转变到聚焦运动变化的整个过程，关注运动时图形中点、线、面的变化，不仅需要掌握图形运动的相关要素，而且需要观察想象、比较思考图形运动留下的轨迹。轨迹扫过形成的图形时常是多元的、无痕的，于是，就有了深入研究的素材。学生对过程的想象远比常规对结果的观察更有挑战性，也就更有利于其直观想象素养的培养。

二是在比较异同中建立数学模型。想象运动过程的轨迹图形，比较运动前后的“变”（异）与“不变”（同）要素，也是一种建立数学模型从而解决问题（解释结论）的过程。这样的过程很有挑战性，是对学生直观想象、推理能力、模型意识、应用能力等的综合考验，也有助于学生进一步把握图形运动的特征和规律。

三、实践案例

小学阶段，教学图形运动的单一方式（如平移、旋转、轴对称等）时，教师一般会采用“出示运动方式—按照规定画图—归纳运动特点”这样的模式（流程）。关于图形运动的综合学习（特别是与解决实际问题结合的学习）相对较少，直观想象运动变化的体验非常缺乏，造成学生解决与图形运动相关的实际问题时出现困难。

我们用“在一个边长为6 cm的正方形中有一个直径是4 cm的圆，现将这个圆在正方形内任意移动，它不能接触到的面积有多大？”这个问题对城区某学校的315位六年级学生进行检测，发现接近三分之二的学生解答错误，甚至有27.9%的学生完全没有思考方向，呈现的答案与正确答案相距甚远。这样的结果表明，学生在解决与图形运动相关的实际问题时，直观想象能力不足，想象不出图形运动的过程，抽象不出解决问题的模型。

因此，我们在六年级设计并实施了《图形的运动》综合练习课。下面，以这节课为例，具体阐述图形运动学习中直观想象运用（相关问题解决）的变化与比较策略。

（一）想象运动轨迹，系统感受图形运动的变化规律

【教学活动1】 将一条线段作运动

师 一根长4厘米的线段运动后，轨迹扫过的面可能是怎样的图形？想象一下。

生  长方形。

师 怎样的长方形？怎样得到的呢？

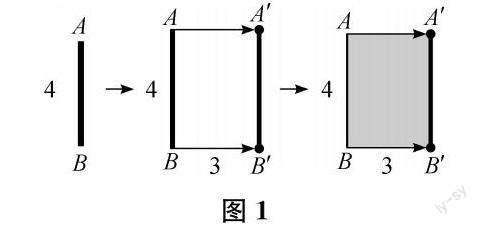
生 比如线段向右平移3厘米，轨迹经过的面就是一个长4厘米、宽3厘米的长方形。

（教师引导学生想象线段运动的过程，然后利用动画演示，画面定格为图1。）

师  除了得到长方形，还有不同的图形吗？

生  得到一个圆。

师  一个圆？想象一下，会是多大的圆？

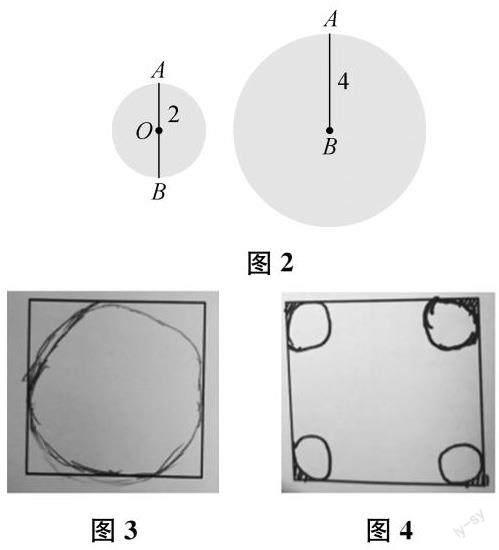
生  半径2厘米的圆。绕中点O顺时针旋转180°即可。

生 还可以是半径4厘米的圆。以线段的一端为中心，顺时针旋转360°即可。

……

（教师引导学生想象线段运动的过程，然后利用动画演示，画面定格为图2。）

师 将一条简单的线段作运动，因为运动的关键要素不同，轨迹可以是多个不同的图形。

从一条简单线段的运动开始探究，感受轨迹扫过的面，学生容易接受和理解。教学时，先让学生想象通过怎样的运动可以得到怎样的轨迹图形，再由学生描述或板演，最后动画演示过程，从而不仅巩固图形运动的要素，也让学生初步感知运动的轨迹图形。

【教学活动2】 将一个三角形作运动

教师将线段换成三角形，让学生想象其运动后轨迹可能是怎样的图形。

研究三角形运动后轨迹形成的图形，相对复杂得多。特别是旋转，因为旋转中心和角度的不同，轨迹形成的图形可能是一个不规则的图形，需要想象其中的某段圆弧。完成这样的活动，不仅需要回忆图形运动的相关知识，更需要将图形运动的相关知识综合起来考虑，既可以通过平移去想象，也可以通过旋转去想象，当然还可以通过轴对称去想象。因为图形运动知识的应用是开放的，所以其探索形成的结果（包括轨迹）也是开放的，从而便于学生将所学知识纳入系统中去分析、思考、想象与应用。

（二）比较变化要素，切实体会图形运动的模型价值

“图形的运动”的学习不仅有想象运动过程、描述运动特征、体会运动规律的要求，而且有学以致用，解决有关实际问题的要求。运用图形运动的知识解决实际问题，其关键在两个地方：一是想象生活中实物的运动情形，比较变化要素；二是结合情境分析，建立问题模型。

【教学活动3】 计算扫地机器人的清扫面积

师 有一台直径40厘米的圆形扫地机器人，要清扫一间储物间的地面，储物间的地面正好是一个边长为1.4米的正方形。如果机器人可以在储物间地面上任意移动，它能清扫到全部地面吗？若不能，则清扫不到的地面有多大？

（学生自主尝试画图、计算。）

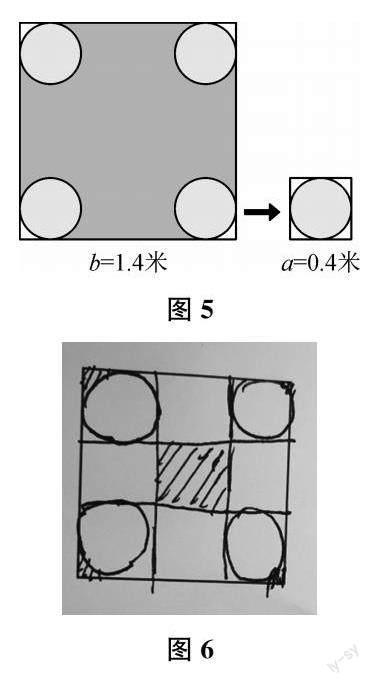
师 （展示学生画出的两种图形，如图3、图4所示）这两种画法表示出了清扫不到的部分？你认为哪种画法是正确的呢？

（學生小组讨论，然后全班交流。）

生 我们小组认为第二种画法是正确的。因为扫地机器人是直径40厘米的圆，所以四个角上，空白部分应该跟直径40厘米的圆有关。第一个图形中，圆太大了，空白部分也太大了。

生  可以拿一个小圆在正方形里运动试一下。只需把这个圆放在正方形的四个角上，空白部分就是清扫不到的地方，其他地方都可以通过平移清扫到。

（该生上台，操作课件，形成下页图5。）

比较哪种画法是正确的，实际是建立数学模型的过程。在讨论中，通过直观演示，帮助学生想象与理解四个角清扫不到的部分正好是圆形扫地机器人与正方形地面一个直角形成的“外方内圆”部分，从而建立适当的数学模型，突破解题的难点。

【教学活动4】 限制运动范围，计算扫地机器人的清扫面积

教师出示变式问题1：想象一下，如果机器人沿储物间地面的四周清扫一圈，它清扫不到的地面有多大？与之前的问题相比，有哪些相同的地方，有哪些不同的地方？让学生尝试解决。

限制平移运动的范围，从圆在正方形内任意平移到只沿四周平移，对想象的要求更高了，特别是得到中间的空白部分是一个正方形。如何帮助学生想象、理解呢？可以选取圆周的上下左右4个点进行平移，形成4条线段，就是圆形平移的边界（如图6所示），从而帮助学生想象、理解为什么形成的是一个正方形，而不是有弧线的图形。

【教学活动5】 改变生活事件，比较割草机的割草面积

教师出示变式问题2：工人用一台清扫面为半圆形（其半径为20厘米）的割草机在一块草坪上割草，割草机分别向右平移10米、向下平移10米（如图7所示），轨迹扫过的面积一样大吗？若不一样，则相差多少？让学生尝试解决。

改变生活事件，一则拓展学生的视野，使其了解图形运动在生活中广泛存在；二则仍然着眼于运动过程的想象与数学模型的建立，突出想象能力、思维能力的发展。事实上，从图形运动与问题核心的关系来看，解决这一问题的最佳方法是比较两个长方形的面积。

总的来说，《图形的运动》综合练习课，没有停留在基本知识和基本技能的操练上，而是以变化与比较的视角，聚焦运动过程形成的轨迹图形，让课堂有想象和思辨的空间与挑战，从而帮助学生在解决生活实际问题的过程中自主建立数学模型，提升综合数学素养。