图形概念形成中直观想象的运用

李苗苗 吴晓敏

摘 要：直观想象在图形的认识中有着重要的作用。图形概念形成中直观想象的运用，可以借助感知与抽象的策略，具体有直观描述、观察理解、想象推理三个层次。由此，《平行与垂直》一课的教学，可以引导学生经历如下三个环节：由“画”到“说”，借图形特征发展直观描述水平；由“一”到“多”，借图形辨析发展观察理解水平；由“聚”到“联”，借图形要素发展想象推理水平。

关键词：小学数学；直观想象；图形概念；平行与垂直

一、直观想象与图形的认识

直观想象是认识事物的基本方式。作为直观想象的重要载体，图形是数学研究的基本对象之一。在数学教学中，利用图形可以简单、直接地描述问题，探索和形成思路，寻找和发现结论，记忆和理解知识以及建立良好直觉，把握本质规律。

学生对图形的直接感知是直观的，但对图形的特征描述等数学概念认知则是抽象的。在数学学习中，学生对空间图形的认识，往往是根据已有经验，在直接观察的基础上，加以想象、抽象的过程。简言之，学生借助空间形式观察、想象图形的形状大小、位置关系、形态变化与运动规律，最终推理得到图形的具体特征等抽象概念。

图形是空间表征的重要形式，是直观的载体、想象的源头。由此可见，直观想象的关键就是感知、发现图形与分析、解读图形，进而理解和掌握图形的要义。因此，在图形教学中，恰当引导学生感知图形、分析图形，将图形反映出的数量关系直观化并进行想象加工，是进一步建构数学知识、解决数学问题、发展直观想象能力的关键路径之一。

二、策略要义

一是感知。感知是意识对内外界信息觉察、感觉、注意、知觉的一系列过程。感知可以分为感觉过程和知觉过程。感觉能够反映物体的属性，如通过眼睛、耳朵等感官看、听。知觉是把感觉到的物体的各个属性有机结合起来，成为一个整体的过程。二是抽象。抽象是从众多的事物中抽取出共同的本质特征，舍弃非本质特征的过程。具体地说，抽象就是在实践的基础上，对丰富的感性材料，通过去伪存真、去粗取精、由表及里地加工制作，形成概念、判断、推理等思维形式，从而反映事物的本质和规律的方法。［1］

学生通过对图形的直观感知，经过大脑的加工想象，抽象出本质含义，最终习得知识，发展能力，便是图形概念形成中直观想象运用的一种策略。具体可以阐释为直观描述、观察理解、想象推理三个层次。

直观描述是指根据事物的外表形状确认和操作几何对象，把图形看成一个直观的整体，将自己感受到的事物的形态与变化用语言表达出来，并在思维中形成视觉表象。

观察理解是指对既有感知经验的再现。观察是知觉的高级形态，是有目的、有计划、较持久的知觉过程。在直观感受和语言描述后，通过对几何图形的观察以及特征的分析、归类，对图形的性质等有一定的理解与掌握。

想象推理是指在感知观察几何图形变化发展的基础上，经历知识的扩展、猜想、验证，推理得到图形的变化趋势、发展规律，并加工形成自己的经验认知的过程。

三、实践案例

现以人教版小学数学四年级上册《平行与垂直》一课为例，具体阐述图形概念形成中直观想象运用的感知与抽象策略。

本课的教学内容主要是探究同一平面内两条直线的位置关系，它以认识线和角等概念为基础，是后续学习平行四边形和梯形等内容的基础。基于对教材前后连贯以及学生直观想象发展的思考，本课的学习目标可以这样确定：借助直观的实物或图形，依托空间想象能力，探索同一平面内两条直线不同的位置关系，进而理解和掌握平行概念与垂直概念，发展空间意识和直观想象素养。

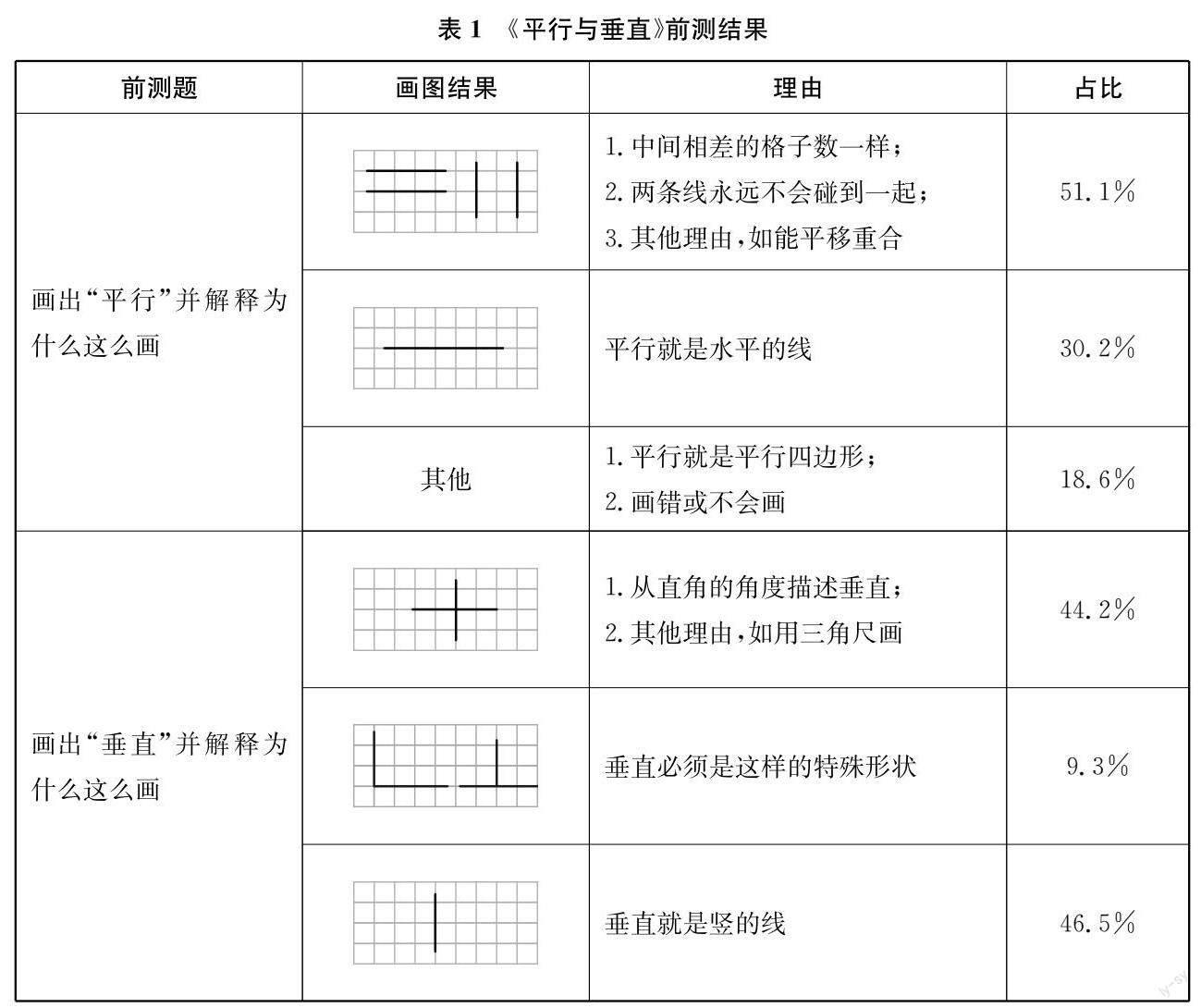
虽然教材在编排上结合了动手操作与生活情境，但总体来说，内容的抽象性仍然较强，对学生的几何直观、空间观念要求较高。由前测（结果如下页表1所示）了解到，无论是对“平行”还是对“垂直”，学生的理解尚停留在表面，且有一些偏差。具体来说，多数学生虽然能画图表征平行，但认识比较粗浅，表现为画出的平行大多数是横平的两条线，偶尔会出现纵向、斜向的情况；部分学生只画了一条水平的线，表明他们对平行的前概念是“平的线”。另外，多数学生不能画图表示垂直，错误地将垂直理解为一条竖直往下的线等；而部分画对的学生，也说不清楚什么是垂直。

基于以上对教学内容和学习基础的分析，我们尝试借助感知与抽象策略，逐步展开本课的教学。下面，以“平行”的教学为例具体说明。

（一）由“画”到“说”，借图形特征发展直观描述水平

从直观的图形到关于特征的语言描述，是认识事物、抽象概念的基础。平行这样的图形概念在生活中不单独存在，需要借助事物来表征。因此，学生需要有一个由经验认知到数学抽象的发展过程。

【教学片段1】

教师提出任务：你觉得什么是“平行”？请在方格纸上画一画。

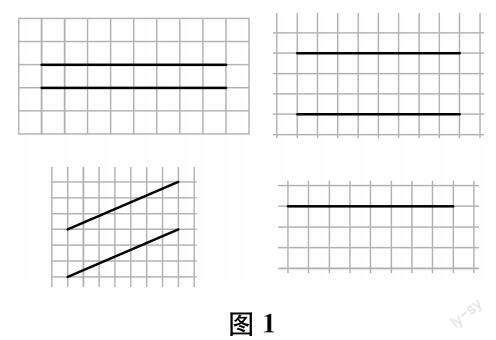
学生完成后，教师呈现学生的作业（如图1所示），并提出要求：请你根据自己的作品，同桌互相说一说什么是平行。

学生同桌交流后，教师组织全班反馈，并要求思考：把两条直线无限延长，它们仍然平行吗？引导学生想象“直线无限延长”的动态过程，随后课件演示。

……

平行线是同一平面内两条直線位置关系的一种表现。很多教师在教学时，会从研究两条直线的位置关系入手。这里，由“借助方格画平行线”入手，打破传统“引导发现”的学习方式，采用唤起认知经验、完善改造经验的学习方式，不失为一种教学创新。以上教学过程体现了两个层次的引导：一是引导学生画“平行”，展示自身经验中的图形认识水平，初步感知平行线的特点；二是引导学生用口头语言描述“互相平行”，将具体的图形意象提炼为语言意象，继而对已有认知经验进行思辨和完善。

（二）由“一”到“多”，借图形辨析发展观察理解水平

观察理解是数学思维形象化的表征，一般通过观察、操作和描述等行为表现出来。为了更好地帮助学生认识平行，要引导学生从更多的图形中获取观察理解的经验。

【教学片段2】

教师结合学生初步获取的经验，组织学生完成下面的练习：

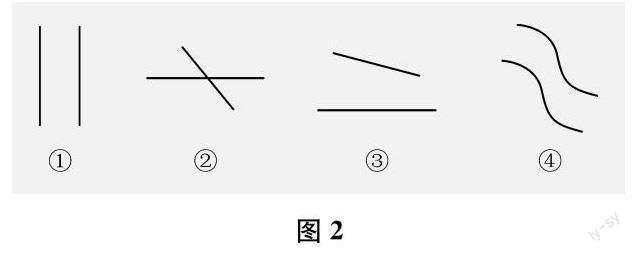
1.观察图2中的各个图形，判断哪些是平行线。

2.观察正方体模型，判断两条直线的位置关系：先看同一平面上的两条直线，再看不同平面上的两条直线。

这里，从观察平面图形而后判断到观察立体图形而后判断的逐层推进，均在引导学生观察更多的平行线，丰富直观感知经验。同时，也在有意识地引导学生通过交流探讨，发展观察理解水平。特别是对异面直线的判断，既需要对同一平面上平行线概念的理解，又需要对不同平面上直线的想象推断；是在直观经验较为丰富的基础上的进一步历练，有意识地提高了认识的难度。

（三）由“聚”到“联”，借图形关系发展想象推理水平

学生理解平行概念后，需要在更复杂的图形背景中联系相关概念（如垂直）进行综合应用，从而借助图形关系发展想象推理水平，使直觉思维与逻辑思维相互协调、相互融合。

【教学片段3】

教师提出以下问题，让学生思考回答：

1.图3中哪些线互相平行？请说明理由。

2.你在生活中见过平行吗？想想其中蕴含着什么道理？

问题1是数学概念的直接应用，让学生结合平行概念的要素，从众多线段中寻找互相平行的位置关系。一是需要对平行概念的理解，二是需要借助图形要素分析判断两条直线之间的位置关系。如线段AF与BC的平行关系，需要借助同时垂直于直线CG推理得出。

问题2是数学概念回归生活的应用，考查学生对平行概念掌握的深度和广度以及发散思维。学生可能举出直线跑道的分隔线、竹竿水平掉进水里引起的水面波纹等例子，进而思考（猜测）其背后的道理。这一过程中，不仅可以利用实物印证，而且可以不利用实物，完全通过想象来确认和说明。

总之，图形在生活中不是孤立存在的，而是依附于具体的事物展现出来的，因此，感知与抽象是认识图形的重要过程；当然，对图形的感知与抽象需要空间想象做支持，因此，認识图形的过程往往也是直观想象应用与发展的契机。

参考文献：

［1］ 冯回祥.思维方法与数学教学［M］.武汉：华中科技大学出版社，2018：100.