多样性诱导的潜在嵌入多视图聚类

张绎凡 ,李婷 ,葛洪伟*

（1.江南大学人工智能与计算机学院，无锡，214122；2.江苏省模式识别与计算智能工程实验室(江南大学)，无锡，214122）

聚类是数据挖掘和模式识别领域中的一个重要分支，是一种无监督的机器学习算法，旨在将数据集分成由类似的数据对象组成的多个类.过去，传统的单视图聚类占主导地位，随着聚类技术的发展，单一视图提供的信息有限，传统单视图聚类的研究到了瓶颈阶段，因此对同一个数据的多角度描述应运而生.多视图是指从不同角度对同一事物进行描述的视图集合，例如，图像可以通过颜色、纹理、形状等不同特征进行描述，网页数据可以由图像、文本、超链接等进行描述，传感器信号有时域和频域上的分解［1］.这些都是多视图数据，它们虽然表现出异质性，但本质上具有潜在相关性和多样性.

多视图聚类旨在利用视图之间互补的特性，分析相互之间的关系，构建完善的约束，最终提升聚类效果.多视图聚类大致可分为四种：（1）基于协同训练的多视图聚类.受协同训练的思想启发，Nigam and Ghani［2］将最大似然估计的思想与协同训练相结合.Kumar and Rai［3］强制不同的视图进行共同正则化，最小化不同视图之间的拉普拉斯矩阵对应的特征向量.（2）基于多核学习的多视图聚类方法，旨在探索多视图数据的非线性结构.Huang et al［4］提出一种同时执行多视图聚类任务并学习内核空间汇总相似性关系的模型.由于该模型没有考虑权重分配问题，Liu et al［5］根据每个视图的每个内部簇分配的权重提出一种用于多视图聚类的聚类加权核k均值方法.（3）基于图学习的多视图聚类方法，目标是在所有视图中找到融合图.Zhan et al［6］提出一种根据每个视图的优化图获得全局图的多视图谱聚类.（4）基于子空间学习的多视图聚类方法.Wang et al［7］为了提高信息互补的实际效果，增强了不同视图对应的子空间之间的排他性.Zhang et al［8］采取增强信息互补的另一种思路，设计自适应样本加权策略以及自适应低级多内核学习来加强子空间自表示.这些方法大都直接计算数据集中的原始特征，存在噪声与误差，不能很好地适应较多视图的数据.

针对上述问题，Zhang et al［9］提出潜在嵌入空间的概念，通过间接方法获取数据集中的特征，并利用该潜在嵌入表示进行聚类.Huang et al［10］在Zhang et al［8］的研究基础上提出共享信息的优化，使潜在嵌入表示更准确.由于现有的二次规划求解较复杂，Chen et al［11］将二次规划求解法改进为拉格朗日乘子法，进一步提升潜在嵌入多视图聚类算法的效率.MCLES（Multi‐View Clustering in Latent Embedding Space）［12］在Zhang et al［8］的基础上结合全局相似性学习以及聚类指标学习进行聚类，取得了较好的效果.但上述方法在潜在嵌入学习过程中仅仅注意了投影矩阵的相关约束，没有充分利用视图之间隐藏的多样性信息，缺少局部信息的约束项，导致潜在嵌入空间存在部分信息无法被合理利用的问题.

为了解决上述问题，提出一种多样性诱导的潜在嵌入多视图聚类算法，多样性指从不同视角学习的子空间表达式具有足够的独立性，能够有效地利用不同视图之间的互补信息.该方法将希尔伯特施密特独立准则（Hilbert Schmidt Indepen‐dence Criterion，HSIC）与MCLES 融合在一个框架中，利用HSIC 平衡不同投影矩阵之间的多样性，提升潜在嵌入学习的结果；同时，对潜在嵌入空间进行全局相似性学习和聚类指标学习，得到一致性亲和矩阵对应的谱嵌入矩阵，并通过k‐means 得到最终的聚类结果.在六个公开数据集上进行的实验证明该算法具有一定优势.

1 相关理论

1.1 符号与定义本文中，粗体大写字母表示矩阵，粗体小写字母表示向量，小写字母表示标量.

定义一个具有V个视图、N个样本数据的多视图数据集X={X1，X2，…，XV}，其中，Di表示第i个视图的维度.对于矩阵X，Xi表示第i行，Xi，j表示第i行第j列的元素.Tr(X)，XT和‖X‖F分别表示矩阵X的秩、转置和Frobenius范数.I表示单位矩阵，1 表示元素全为1 的列向量.

1.2 潜在嵌入空间MCLES 中的潜在嵌入空间方法为每个数据点推断一个共享的潜在表示R∈Rd×N，其中，d为潜在嵌入空间的维度，假设所有不同的视图都起源于一个潜在的表示R.具体地，如图1 所示，不同视图可以用它们各自的投影矩阵{P1，…，Pi}进行重构，其中，Pi∈RDi×d，每个视图的样本数据表示为Xi=Pi Ri，i=1，2，…，V，并具有共享的潜在表示R.潜在嵌入空间方法和子空间自表示方法相比是一种全新的理论方法，能够较全面地恢复数据隐藏的空间结构，对最后的聚类效果有较好的提升.

图1 潜在嵌入空间示意图Fig.1 Latent embedding space

MCLES 最终的目标函数式如下：

2 多样性诱导的潜在嵌入多视图聚类

2.1 算法模型根据式（1）的目标函数可知，MCLES 在数据样本矩阵和投影矩阵的学习过程中仅仅注意了潜在嵌入学习，缺少局部信息的约束项.多视图数据在不同视图之间具有差异，即多样性信息，所以MCLES 忽略了不同视图之间的多样性.为了解决这个问题，受Cao et al［14］的启发，采用经验的HSIC 约束特定于视图的投影矩阵.HSIC 具有以下特性：（1）通过将变量映射到一个再生希尔伯特空间来度量变量之间的依赖性，因此可以度量变量之间较复杂的关联，适用于非线性相关的情况；（2）在测量变量依赖性时，不需要估计变量的联合分布，具有计算优势；（3）经验的HSIC 可以被证明等价于矩阵乘积的迹运算，使方法更易求解且具有良好的收敛性.因此，引入HSIC 可以更好地平衡不同视图矩阵之间的独立性和相关性.

给定Z：={(x1，y1)，…，(xn，yn)}⊆X×Y，Z 为用于产生一系列n个联合分布Pxy的独立观测数据.经验HSIC 记作HSIC(Z，F，G)，可以被写成如下形式：

其中，K，L∈Rn×n是Gram 矩阵且有kij=k(xi，xj)，lij=k(yi，yj)，k(xi，xj)和k(yi，yj)分别是X 和Y上的核函数.hij=δij-1/n将Gram 矩阵中心化，使数据在特征空间具有零均值.

利用经验性HSIC 约束可以更真实地反映不同视图之间的关系，提出多样性诱导的潜在嵌入多视图聚类模型（DiMCLES）.目标函数如下：

2.2 算法优化在得到目标函数后采用交替迭代对目标函数求解，以下是求解的详细过程.

固定R，Z，F，求解P，去除无关项，式（3）等价于优化以下问题：

直接计算矩阵P较困难，为了有效地解决这个问题，将其划分为V个子问题：

在计算Pm时，矩阵Pn(n≠m)是固定的.为了方便，采用内积核作为HSIC 的内核，即Km=PmT Pm，因此HSIC 可以写成：

对式（7）求偏导并令其为零，得到矩阵针对每个视图的更新式：

固定P，Z，F，求解R，去除无关项，式（3）等价于优化以下问题：

使用交替向乘子法（Alternating Direction Method of Multipliers，ADMM），引入辅助变量A1，A2代替R，得到相对应的增广拉格朗日函数为：

对A1和A2求偏导并令其为零，得到A1，A2以及Y的更新式：

固定P，R，F，求解Z，去除无关项，式（3）等价于优化以下问题：

为方便求解，引入变量M，令M=ZT Z，式（12）可以写成以下形式：

对式（13）按列展开得到：

式（15）是一个标准的二次规划问题，可用现成的二次规划包［15］对其进行求解.

固定P，R，Z，求解F，去除无关项，式（3）等价于优化以下问题：通过计算矩阵Z的c个最大特征值对应的c个特征向量得到谱嵌入矩阵F的解.

2.3 算法流程和时间复杂度分析算法流程如下所示.

3 实验设置

3.1 数据集介绍在六个广泛使用的数据集上进行相关实验：3Sourses［11］，Notting‐Hill［11］，Yale［12］，MSRCv1［12］，ORL［12］，BBCSport［12］.数据集的具体信息如表1 所示.

表1 实验使用的数据集介绍Table1 Introduction of datasets used in experiments

3Sourses：是多来源的新闻数据集，包含来自BBC、卫报和路透社的新闻，由来自六个类的169个新闻对象组成.实验中使用了三个视图，分别为BBC（视图1）、卫报（视图2）和路透社（视图3）.

图2 DiMCLES，LMSC 和MCLES 在六个基准数据集上的收敛曲线Fig.2 Convergence curves of DiMCLES，LMSC and MCLES on six benchmark datasets

图3 在六个基准数据集上根据ACC对α，β，γ，λ和d 的参数分析Fig.3 Parameters analysis on α，β，γ，λ and d in terms of ACC on six benchmark datasets

Notting‐Hill：是从电影《Notting‐Hill》中获得的视频人脸数据集，包含4660 张人脸图像.每个演员为一个类别，选择五个主要演员的面孔，随机采样每个演员的110 张面部图像.实验中使用了三个视图，分别是强度特征（视图1）、LBP 特征（视图2）和Gabor 特征（视图3）.

Yale：是广泛使用的人脸图像数据集，由15个不同主题的灰度图像组成，每个主题由11 张图像组成，共165 张.图像的变化包括右光、中心光、左光、是否戴眼镜、是否快乐、正常、惊讶、眨眼和困倦.实验中使用了尺寸分别为4096（视图1）、3304（视图2）和6750（视图3）的三个视图.

MSRCv1：是一个图像数据集，由属于七个类别的210 个对象组成，分别是飞机、建筑、树、汽车、牛、脸和自行车.实验中使用了四个视图，分别为CM 特征（视图1）、GIST 特征（视图2）、LBP特征（视图3）和GENT 特征（视图4）.

ORL：是广泛使用的人脸图像数据集，由属于40 个不同主题的400 张人脸图像组成，每个主题包含10 张图像.每个主题的图像都在不同的时间、光线、面部表情（是否睁眼、是否微笑）和面部细节（是否戴眼镜）下拍摄.实验中使用了三个视图，分别为强度特征（视图1）、LBP 特征（视图2）和Gabor 特征（视图3）.

BBCSport：是一个文档数据集，由2004-2005 年五个主题领域的BBC Sport 网站体育新闻的544 个文档组成，分别是商业、体育、政治、娱乐、科技.实验中使用了两个视图，其维度分别为3183（视图1）和3203（视图2）.

3.2 对比算法介绍将本文提出的方法与10 种多视图聚类方法进行比较：

SC（Spectral Clustering）：对每个视图进行单视图谱聚类，取多个视图中最好的数据，记作SCbest.

ConcatePCA‐SC：是SC 方法的扩展，使用PCA 方法降维所有视图的特征.

Co‐Reg（Co‐Regularized Spectral Cluster‐ing）：强制所有视图执行共同正则化［2］.

Co‐Training（Co‐Training Multi‐View Clus‐tering）：将最大似然估计与协同训练相结合［16］.

Min‐Disagreement（Spectral Clustering with Two Views）：是基于最小化分歧的多视图谱聚类［17］.

RMSC（Robust Multi‐View Spectral Cluster‐ing）：是使用马尔可夫链进行聚类的鲁棒多视图谱聚类［17］.

LMSC（Latent Multi‐View Subspace Cluster‐ing）：根据多个视图的共同潜在结构发现子空间结构［9］.

MVGL（Graph Learning for Multi‐view Clus‐tering）：根据每个视图的优化图获得全局图［6］.

MCLES：根据视图的潜在结构进行潜在嵌入学习、全局结构学习［12］.

LSRMSC（Latent Shared Representation for Multi‐View Subspace Clustering）：是恢复潜在共享表示的多视图聚类［10］.

3.3 实验结果与分析使用精度（Accuracy，ACC）、标准化交互信息（Normalized Mutual In‐formation，NMI）、纯度（Purity，PUR）、兰德指数（Rand Index，RI）作为聚类指标，指标的数值越高，表示聚类效果越好.由于算法和最后的k‐means 算法框架存在随机性问题，因此实验进行20次，结果取20 次的平均值以及标准差.

表2～7 给出了不同算法在六个公开数据集上的聚类实验结果，表中黑体字表示结果最优，括号中的数字为方差，表7 中的NA 表示该算法不适合该数据集对应的聚类指标.

表2 不同算法在3Sources 数据集上的聚类表现Table 2 Clustering performance of different algo⁃rithms on 3Sources

表3 不同算法在Notting⁃Hill 数据集上的聚类表现Table 3 Clustering performance of different algo⁃rithms on Notting⁃Hill

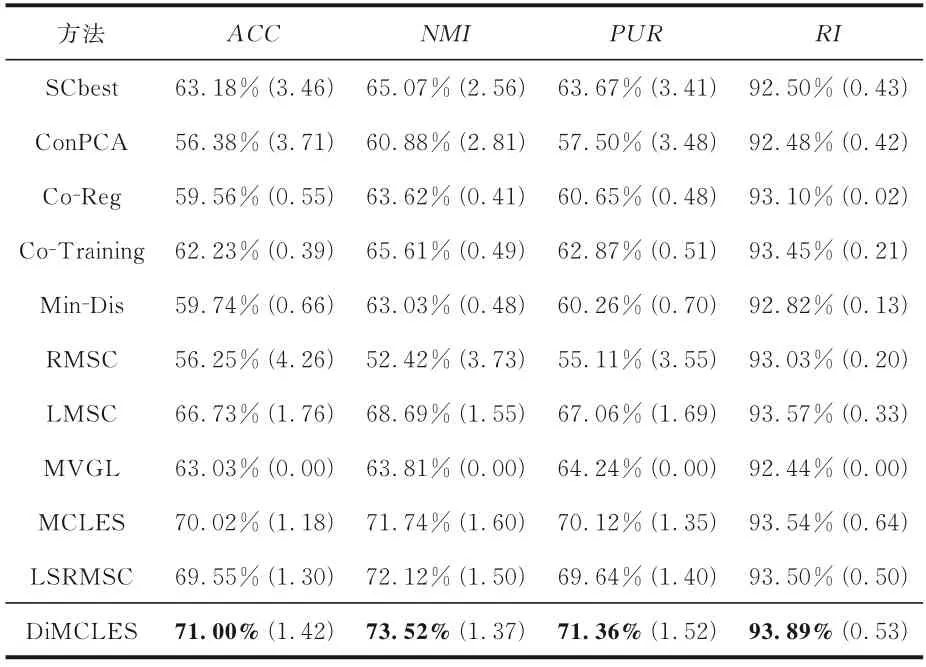
表4 不同算法在Yale 数据集上的聚类表现Table 4 Clustering performance of different algo⁃rithms on Yale

表5 不同算法在MSRCv1 数据集上的聚类表现Table 5 Clustering performance of different algo⁃rithms on MSRCv1

表6 不同算法在ORL 数据集上的聚类表现Table 6 Clustering performance of different algo⁃rithms on ORL

表7 不同算法在BBCSport 数据集上的聚类表现Table 7 Clustering performance of different algo⁃rithms on BBCSport

大多数情况下，DiMCLES 优于相关算法或具有一定竞争力，尤其是在3Sources 和Notting‐Hill 上.和MCLES 相比，在3Sources上，Di‐MCLES的ACC提升11.21%，NMI提升5.37%，PUR提升1.42%，RI提升0.43%；在Notting‐Hill上，ACC提升9.95%，NMI提升8.57%，PUR提升7.65%，RI提升3.32%.同时，DiMCLES 在Notting‐Hill，MSRCv1 和BBCSport 上的方差为0，稳定性很好，在其余数据集上的稳定性也不差.但在ORL 上的表现较差，可能是因为ORL 各个视图之间的差异性较大，算法无法很好地将较大的差异性整合到一致性亲和矩阵中.

在多数真实数据集上的实验结果证明Di‐MCLES 算法优于RMSC，LMSC，MCLES，MVGL 等多视图子空间聚类方法，这是因为DiMCLES 能够较好地提取多视图数据不同视图之间的多样性潜在信息.

3.4 收敛性分析为验证DiMCLES 的收敛性，图2 展示了DiMCLES，MCLES 和LMSC（Latent Multi‐View Subspace Clustering）［9］在六个基准数据集上的目标函数图像.由于LMSC 采用零初始化，因此目标函数有一段先上升的过程.由图可见，DiMCLES 在BBCSport 和3Sources 上前10 次迭代急剧下降，在15 次迭代时基本趋于稳定；在其余数据集上均为前5 次迭代急剧下降再趋于平稳.和LMSC 相比，DiMCLES 有较好的收敛性和稳定性，与MCLES 的收敛性总体相似，在Not‐ting‐Hill 和BBCSport 上略有提升.证明Di‐MCLES 的收敛速度较快，基本能在10 次之内达到收敛，且收敛性较好.

3.5 参数分析DiMCLES 算法共有五个参数，在六个基准数据集上分析五个参数对DiMCLES算法精度的影响，实验结果如图3 所示.由图可知，参数α在[ 0.5，1 ]时，算法的稳定性较好.参数β在[ 0.04，0.08 ]时，算法在除了Notting‐Hill以外的其他数据集上均有较好的稳定性，这是由于目标函数在Notting‐Hill 上对非平凡解具有一定敏感性，造成该区间内的ACC存在20%左右的上下波动.参数γ在[ 0.001，0.005 ]时，参数λ在[ 0.2，0.35 ]时，算法的稳定性较好.参数d在[ 40，100 ]时，算法性能趋于平稳，但在40 以下波动较大，这是因为潜在嵌入空间维度过小时，算法无法稳定地描述原始空间的特征，导致ACC出现较大的波动.

3.6 t⁃SNE 可视化分析为了更直观地观察DiMCLES 的聚类性能，采用t‐SNE（t‐Distribut‐ed Stochastic Neighbor Embedding）将每个视图的原始特征及一致性亲和矩阵映射到二维空间，对得到的降维样本点进行可视化分析.为了方便观察，选取聚类数较少的MSRCv1 和3Sources 进行数据可视化分析，实验结果如图4 所示，图中不同颜色表示不同聚类类别.由图可见，DiMCLES在MSRCv1 上较好地保留了原始数据（视图2 和视图4）的底层结构，不同颜色的簇内间距比LMSC更紧凑.DiMCLES 在3Sources 上保留了原始数据视图部分的底层结构，和LMSC 相比，在呈现聚类底层结构上有较明显的提升.因此，DiM‐CLES 算法得到的一致性相似表示比每个视图的原始特征更能体现良好的聚类结构，进一步证实该算法具有一定优势.

4 结论

本文提出一种多样性诱导的潜在嵌入多视图聚类，使用特定于视图的投影矩阵从多视图数据中恢复潜在嵌入空间，提取各个视图中的潜在信息，采用经验的希尔伯特施密特独立准则约束特定于视图的投影矩阵，保留视图之间的信息多样性.在统一的优化框架下进行潜在嵌入学习、多样性学习、全局相似性学习以及聚类指标学习.在真实数据集上的收敛性分析、参数敏感性分析及可视化分析实验证明了该算法在收敛性、参数稳定性以及保留聚类底层结构上具有一定优势.