三支残差修正的时间序列预测

方宇 ,贾春虹 ,吴思琪 ,闵帆*

（1.西南石油大学计算机科学学院，成都，610500；2.西南石油大学机器学习研究中心，成都，610500）

时间序列［1］是把随时间变化发展的过程记录下来而形成的随机变量序列.时间序列预测［2］就是对时间序列数据进行分析，挖掘这些数据的发展规律，并利用挖掘的规律对将来某阶段的数据作出估计.现实生活中，农业、金融、科学和工程等领域每天都会产生大量的时间序列数据，如投资理财［3］、城市数据［4］、社交媒体［5］、天气状况［6］和环境污染等［7］，因此时间序列预测尤为重要.

常用的时间序列预测方法分三类：传统预测方法、人工智能方法和组合预测方法［8］.传统预测方法大多以数理统计为基础，探索数据间的发展规律，建立相应的数学模型，如自回归移动平均（Auto Regressive Moving Average，ARMA）［9］、差分自回归移动平均（Auto Regressive Integrated Moving Average，ARIMA）［10］等.随着人工智能的不断发展，越来越多的学者将人工智能技术应用于时间序列预测的研究任务.人工智能具有强大的自主学习能力和非线性拟合能力，使模型具有更高的预测精度，如LightGBM（Lightweight Gradient Boosting Machine）［11］，TCN（Temporal Convolutional Network）［12］等.但单一预测方法能力有限，所以组合预测方法越来越受到各位学者的青睐，因为组合预测方法充分集成了各单一模型的预测优势，对模型预测性能的提升有显著作用，如STL‐LSTM［13］，TCN‐CBAM［14］等.

三支决策理论最早由Yao［15］提出，其主要思想是针对集合的正域、负域和边界域，分别作出接受、拒绝和延迟的决策，已应用于众多领域，如医学诊断［19］、属性约简［20］、投资决策［21］、文本分类［22］、推荐系统［23］等.如基于三支决策理论的TWDBDL 模型［16］能有效地应用于医学图像分析的不同阶段，实现在皮肤癌分类问题中的不确定性量化.三支对话推荐问题［17］由三支推荐与对话推荐组合而成，针对该问题设计的融合对话推荐算法在平均成本方面有一定优势.受三支决策理论的启发，三支聚类［18］能有效地反映对象与聚类之间的不确定关系，将其定义为确定属于、确定不属于和无法确定.

虽然目前针对三支决策理论和时间序列预测已有大量研究，但极少有学者将三支决策理论应用于时间序列预测的研究任务.本文提出一种三支残差修正的融合时序预测模型（Double TCN and LightGBM with Three‐way Residual Error Amendment，DT‐LGBM‐3WREA）.该模型首先使用时序分解算法STL（Seasonal‐Trend Decom‐position Procedure Based on Loess）将时间序列分解为趋势项、周期项和余项；然后，结合各分量特点及模型预测优势，对每个分量单独预测.在余项预测的基础上，结合三支决策理论设计了三支残差修正算法（Three‐way Residual Error Amend‐ment，3WREA）.该算法根据三支决策的评价函数与阈值对，能够将余项预测过程中产生的残差控制在一定范围内，通过修正残差进一步修正余项预测结果，提高模型的预测效果.最后，将三个分量的预测值进行加和得到最终的时间序列预测值.本文的主要贡献：

（1）结合三支决策理论，提出三支残差修正算法3WREA，能够有效地修正残差.

（2）将3WREA 应用于时间序列预测，结合TCN 与LightGBM，提出DT‐LGBM‐3WREA 融合时序预测模型，有效提升时间序列的预测精度.

（3）在不同领域的九个数据集上进行对比实验，实验结果证明了本文模型的有效性.

1 相关工作

1.1 TCN时间卷积网络TCN［24］有两个显著特征：第一，架构中的卷积是因果的，不会发生信息泄露；第二，可以根据任意长度的输入序列映射相同长度的输出序列.实际上，TCN 由因果卷积与一维全卷积网络组合而成，其中，因果卷积保证TCN 第一个特征的实现，一维全卷积网络保证TCN 第二个特征的实现.另外，TCN 引入膨胀卷积，允许间隔采样，这是因为在处理较长依赖关系时，因果卷积需要线性堆叠更多的层，增加了神经网络的深度.总体上，TCN 在各类序列建模任务中表现良好，是一个非常强大的序列建模工具包.

1.2 LightGBMLightGBM［25］是一种高效的梯度提升决策树算法，在处理高维海量数据时能加快模型训练速度，减少内存占用.它在传统的梯度提升决策树（Gradient Boosting Decision Tree，GBDT）上引入基于梯度的单面采样（Gradient‐Based One‐Side Sampling，GOSS）和互斥特征捆绑（Exclusive Feature Bundling，EFB）两种算法来处理大量数据实例和特征，其中，GOSS 的目的是减少数据量并保证模型的精度，EFB 减少了特征维度，提升了模型的训练速度.LightGBM 高效灵活，可广泛应用于分类［26］、回归等机器学习任务.

1.3 三支决策三支决策［27］的核心实质上是在二分类的基础上增加延迟决策的策略，它能较好地处理实际问题中的不确定性，符合人类的认知及思维特点，是解决实际问题的有效途径.假设U是一个有限非空集合，C是有限条件集合，三支决策基于条件集合C，通过评价函数v(x)与阈值对(α，β)将U划分为三个互不相交的区域Lregion，M-region，R-region，简记为L，M，R，其中，α≥β，如式（1）所示：

2 三支残差修正的时间序列预测模型

首先对时间序列进行分解，然后对时间序列数据集进行转换，最后详细介绍3WREA 算法与DT‐LGBM‐3WREA 模型.

2.1 时序分解时间序列通常由趋势性、周期性和不规则分量组成［28］.趋势性是一段时间内稳定发展的趋势，周期性是受周期因素影响的规律波动，不规则分量是众多偶然因素对时间序列造成的累积影响.假设给定一时间序列Y，Y（tY在t时刻的数据）可以被看作是趋势项Tt、周期项St与余项Rt的加和：

使用STL［29］将时间序列分解为趋势项、周期项和余项.STL 是应用最广泛的时间序列分解算法之一，主要由内循环和外循环组成，内循环计算趋势项和周期项，外循环调节鲁棒权重.

内循环的具体步骤：

（1）从原始数据Yt中去除上一轮的趋势分量：

（2）使用平滑参数为ns的LOESS 对去除趋势分量的每个子序列做平滑处理，得到序列

经过上述步骤，将t时刻的时序数据Yt分解得到趋势项Tt和周期项St.根据式（2），余项Rt表示为：

其中，k是内循环当前的循环次数.若时序数据中存在离群值，可能导致内循环产生的某些余项值偏大，为此，STL 用外循环来调节鲁棒权重，减少离群值对回归的影响.

2.2 数据集转换由于单变量时间序列缺乏输入特征矩阵，为了尽可能地提高其预测精度，在数据处理阶段，以滑动时间窗口的形式增加由历史数据构成的特征矩阵.转换后的时序数据由输入特征与输出标签组成，即将单变量时间序列数据集转换为监督学习数据集.多变量时间序列同样以滑动窗口的形式增加历史数据，结合时间序列相关影响因素，共同构成输入特征矩阵.假设有时间序列Y={y1，y2，…，ym}，有影响因素组成的特征矩阵X=[x1，x2，…，xm].设置滑动时间窗口大小为i，形成的监督学习数据集如图1 所示，图中x2n代表第二个时序数据的第n个影响因素，nan代表空值.在后续的数据集转换过程中，删除带有nan的数据，形成最终的监督学习数据集.因此，当时间窗口大小设置为i时，从第i+1 个数据起才是有效的时序数据.

图1 滑动时间窗口处理Fig.1 Sliding time window processing

2.3 三支残差修正算法(3WREA)趋势项与周期项均属于规则变动，共同构成时间序列的常规部分，是一个相对稳定发展的状态.余项是构成时间序列的不规则部分，因为受到多种偶然因素的干扰而产生较大波动，对时间序列产生较大影响.因此，在进行时间序列的分析及预测问题上，应当对余项分量进行深入研究.

本文设计了3WREA 算法来修正余项预测过程中产生的残差，残差为真实值与预测值的差.该算法的主要思想：利用TCN 实现对残差序列的良好拟合和预测，根据式（1）将残差圈定在一定范围内，通过修正残差序列进一步修正余项预测结果.如图2 所示，3WREA 算法的实现分三个阶段：第一阶段，TCN 模型预测残差序列；第二阶段，k‐means 算法聚类；第三阶段，三支残差修正.

图2 3WREA 算法的流程Fig.2 The flowchart of 3WREA

第一阶段：利用TCN 模型训练残差，得到相应的预测结果.TCN 模型采用因果卷积，即t时刻的输出yt仅与t时刻之前的输入x1，x2，…，xt有关，可以表示为：

由于因果卷积在较长序列任务中可能会堆叠更多的层，使神经网络的深度增加，因此，TCN 引入了膨胀卷积，允许间隔采样.对于一维输入序列x∈Rn，滤波器f：{0，…，k-1}→R，序列元素s的膨胀卷积运算定义为：

其中，s-d⋅i代表过去的方向，d为膨胀因子，k为滤波器大小.d=1时，不允许间隔采样，此时与常规卷积一致；d>1时，允许间隔采样.

第二阶段：利用k‐means 算法将残差聚类为三簇.k‐means 算法的主要思想是利用距离公式计算各样本到每个簇中心的距离，根据距离度量将各样本划分到与其距离最近的簇，然后不断更新簇中心，直到簇中心不再发生变化.

第三阶段：通过k‐means 算法求得阈值α与β，其中，α为最大簇中心所在簇的最小值，β为最小簇中心所在簇的最大值.根据式（1），将残差预测序列划分为L，M，R三个互不相交的区域，将R中的残差赋值为α，L中的残差赋值为β，M中的残差保持不变，得到三支残差修正后的残差序列.

3WREA 算法的实现如算法1 所示.

详细说明如下.

步骤1：结合2.2，利用滑动窗口向数据集增加特征矩阵，并进行特征与标签分离操作.DX为特征集，DY为标签集.

步骤2：将训练数据集DX，DY以及各超参数传入TCN 模型进行训练，利用训练好的模型得到预测残差序列.

步骤3 和步骤4：初始化聚类簇数，并利用k‐means 算法将残差序列DY聚类为三簇.

步骤5～7：利用排序算法将簇中心按照升序的方式进行排列，得到最小簇中心和最大簇中心所在簇的标签.

步骤8 和步骤9：得到阈值对(α，β)，α为最大簇中心所在簇的最小值，β为最小簇中心所在簇的最大值.

步骤10～18：根据式（1）定义评价函数v(x)，并结合阈值对(α，β)将预测残差划分为L域、M域以及R域.将R域中的残差赋值为α，L域中的残差赋值为β，M域中的残差保持不变，以此将残差圈定在一定范围内，并得到修正残差序列D′.

步骤19：返回修正残差D′.

2.4 三支残差修正的时间序列预测模型 (DT⁃LGBM⁃3WREA)该模型的主要思想：首先利用STL 将时间序列进行分解；然后，结合各分量特点与模型预测优势，采用不同的模型对各分量进行预测，并利用3WREA 算法对余项预测结果进行修正；最后，将各分量预测结果进行加和得到时间序列的预测结果.如图3 所示，DT‐LGBM‐3WREA 模型的实现可以分三个阶段.

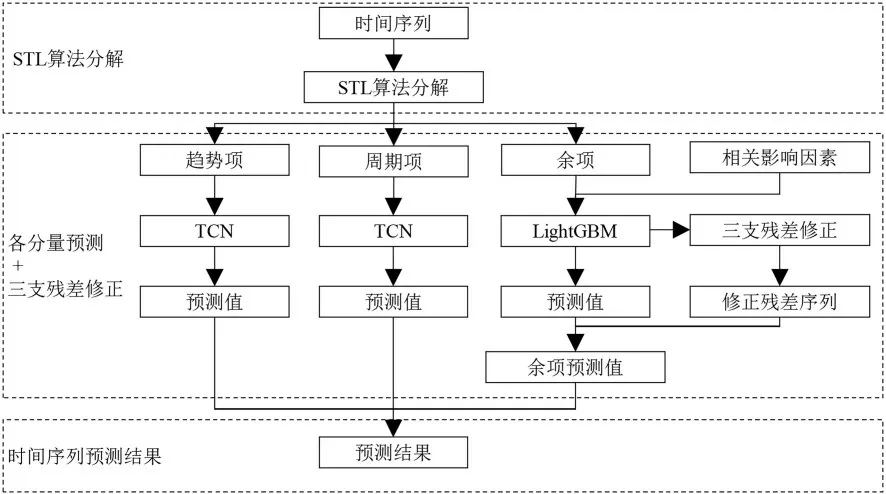
图3 DT⁃LGBM⁃3WREA 模型的流程Fig.3 The flowchart of DT⁃LGBM⁃3WREA

第一阶段：根据式（2），利用STL 算法将时间序列分解为趋势项、周期项和余项.

第二阶段：利用TCN 模型实现对趋势项与周期项的预测.利用LightGBM 模型实现对余项分量的预测，再根据算法1，将该过程产生的残差序列进行三支残差修正.将经过LightGBM 模型得到的余项预测值与残差修正值进行加和，得到余项预测结果.

第三阶段：根据式（2），将各分量预测结果进行加和得到DT‐LGBM‐3WREA 模型的预测结果.

DT‐LGBM‐3WREA 模型的算法实现如算法2 所示.

详细说明如下.

步骤1：若训练集C为多变量时间序列，进行特征与标签分离操作；若训练集C为单变量时间序列，则不进行该操作，直接跳过步骤1.

步骤2：根据式（2），使用时序分解算法STL将时间序列CY分解为趋势项T、周期项S和余项R.

步骤3 和步骤4：利用滑动窗口向趋势项T和周期项S中增加历史数据作为特征矩阵，并对扩充后的数据集做特征与标签分离操作.

步骤5：利用滑动窗口向余项R中增加历史数据作为特征，结合其他时间序列影响因素CX，共同组成特征矩阵，并对新的数据集做特征与标签分离操作，得到特征集RX和标签集RY.

步骤6 和步骤7：利用TCN 模型预测趋势项与周期项，得到趋势项预测值与周期项预测值.

步骤8：利用LightGBM 模型预测余项，得到初步余项预测值R′.

步骤9：将余项真实值R与初步余项预测值R′做差，得到余项残差序列D.

步骤10：结合2.3，利用算法1 对残差序列D做三支残差修正，得到修正残差序列D′.

步骤11：将初步余项预测值R′与三支残差修正后的残差序列D′进行加和，得到余项预测结果.

步骤12：根据式（2），将趋势项预测值、周期项预测值和余项预测值进行加和，得到时间序列预测值.

步骤13：返回时间序列预测结果.

3 实验

为了验证DT‐LGBM‐3WREA 模型的预测性能，在不同领域的九个时间序列数据集上进行对比实验，并与TCN，LightGBM，CNN（Convo‐lutional Neural Network），LSTM（Long Short‐Term Memory）以及DT‐LGBM（Double TCN and LightGBM）进行对比.

3.1 数据集使用不同领域的九个时间序列数据集，表1 给出了数据集的关键信息，包括数据集名称、属性数量、样本数量以及数据集概述等.

表1 实验使用的数据集描述Table 1 The description of datasets used in experiments

3.2 评估指标采用平均绝对误差（Mean Ab‐solute Error，MAE）与均方根误差（Root Mean Square Error，RMSE）评估各模型的预测效果.MAE与RMSE的计算如下所示：

其中，y=y1，…，yn是真实值,是预测值.MAE与RMSE越小，说明模型的预测效果越好，反之则模型效果越差.

3.3 实验设置按照6∶2∶2 的比例将数据集划分为训练集、验证集与测试集.验证集调整模型的超参数，提高模型的预测效果，图4a 和图4b 展示了最低温度的趋势项预测过程中对TCN 模型的kernel_size（卷积核大小）和filters（过滤器个数）的调整.TCN 模型的其他超参数：训练轮次为50，学习率为0.001，批尺寸为32.图4c 和图4d 展示了燃气负荷数据集中训练轮次为50，学习率为0.001，批尺寸为32 时的卷积核大小和过滤器个数的调整.

图4 对部分超参数的调整Fig.4 Adjustment of some hyperparameters

采用TCN，TCN 与LightGBM 分别对趋势项、周期项和初步余项值进行预测.在LightGBM预测的基础上，利用3WREA 算法对该过程产生的残差进行修正，得到LGBM‐3WREA 的预测值，即余项的最终预测结果.将LGBM‐3WREA的预测结果与经TCN 预测得到的趋势项、周期项的预测值进行加和，得到DT‐LGBM‐3WREA 的预测结果.各模型均在相同的软件和硬件配置环境下运行：CPU 为i7‐8550U CPU @ 1.80 GHz，RAM 为8 GB，Windows 10，Python 3.8.

3.4 结果分析结合研究思路，各数据集趋势项与周期项的预测结果仅使用TCN 与LightGBM对比，余项的预测结果仅在TCN，LightGBM 和LGBM‐3WREA 之间进行对比.为了提升模型训练速度，在数据处理阶段使用sklearn 库提供的归一化MinMaxScaler 与标准化StandardScaler 方法实现对数据的按比例缩放，使之统一映射到一个特定区间.同理，为了使各分量之间与各数据集之间的实验结果具有一定可比性，各模型的评估指标也采用归一化之后的数据.表2～4 展示了各分量的评估指标对比，表5 与表6 为各数据集整体预测结果的评估指标对比，表中黑体字表示该数据集对应的模型为当前最优.

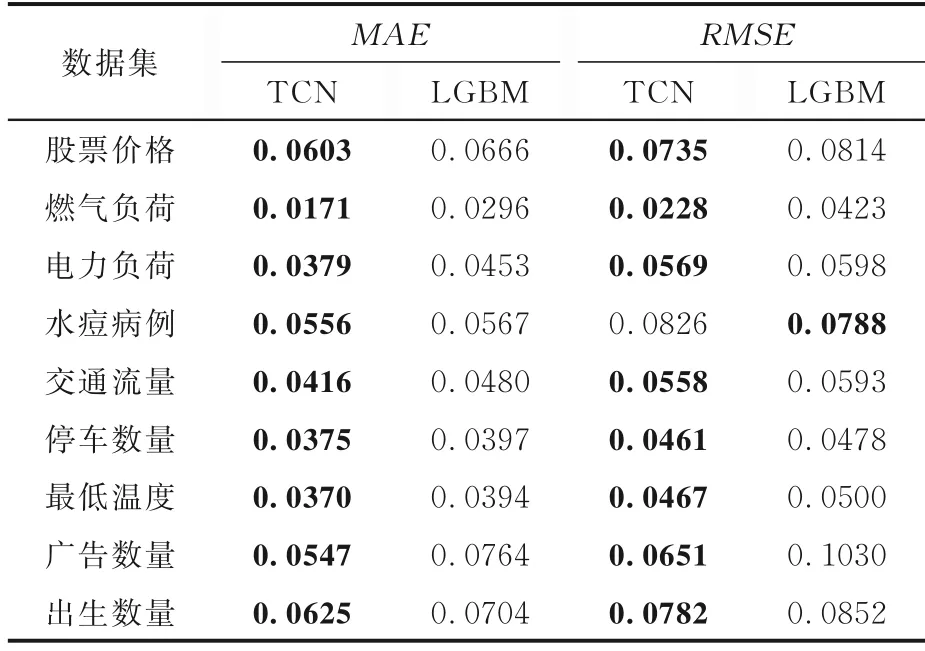
表2 TCN 与LGBM 的趋势项评估指标对比Table 2 Trend item evaluation indicators of TCN and LGBM

表3 TCN 与LGBM 的周期项评估指标对比Table 3 Seasonal item evaluation indicators of TCN and LGBM

表4 TCN，LGBM 和LGBM⁃3WREA 的余项评估指标对比Table 4 Remain item evaluation indicators of TCN，LGBM and LGBM⁃3WREA

表5 本文算法和对比算法在九个数据集上的MAE 指标对比Table 5 MAE metrics of our algorithm and other algorithms on nine datasets

表6 本文算法和对比算法在九个数据集上的RMSE 指标对比Table 6 RMSE metrics of our algorithm and other algorithms on nine datasets

由表2 可见，对于趋势项评估指标，TCN的MAE在九个数据集上表现良好，其RMSE在八个数据集上表现更佳，仅在一个数据集上的预测效果比LightGBM 差.所以，TCN 是预测趋势项的最佳模型.

由表3 可见，对于周期项评估指标，和Light‐GBM 相比，TCN的MAE和RMSE在超过一半的数据集上表现更好.所以，TCN 模型是预测周期项的最佳模型.

由表4 可见，对于余项评估指标，LightGBM的MAE在六个数据集上优于TCN，其RMSE比TCN 多一个数据集的优势.所以LightGBM 是两者中预测余项的最优模型.在LightGBM 预测的基础上增加3WREA 算法修正残差，构成LGBM‐3WREA 模型，其预测效果比LightGBM 更好.因此，3WREA 算法的提出对于余项预测效果的提升具有极大的促进作用.

由表5 和表6 可知，和TCN，LightGBM，CNN 和LSTM 相比，DT‐LGBM 在一半的数据集上表现良好，评估指标的数值更优.在DT‐LG‐BM 的基础上增加3WREA 算法，构成DT‐LG‐BM‐3WREA 模型，结果无论是MAE还是RMSE，DT‐LGBM‐3WREA 模型在超出一半的数据集上的表现更优，其预测效果比DT‐LGBM更出色.所以，3WREA 算法对时间序列预测模型的性能有显著的提升作用.

总体而言，DT‐LGBM‐3WREA 模型在大多数时间序列预测任务上具有明显优势，这是因为3WREA 算法在余项预测任务中表现优异.余项是时间序列受众多偶然因素干扰而产生的不规则变动，在余项预测过程中结合了由各种影响因素组成的特征矩阵，并增加了3WREA 算法对残差进行修正，实现了对余项预测结果的进一步修正，大大提升了DT‐LGBM‐3WREA 模型的预测性能.但由于DT‐LGBM‐3WREA 模型首先需要对时间序列进行分解，再对分解后的各分量采用不同的模型进行预测，并在余项预测过程中增加三支残差修正，导致步骤繁多，时间开销较大.这将是今后进一步的改进方向.

4 结论

本文提出一种三支残差修正的融合时序预测模型.首先将时间序列分解为趋势项、周期项和余项；然后，基于各分量特点与模型预测优势，分别选择不同的模型实现对各分量的预测，并结合三支决策理论，设计3WREA 算法对余项预测结果进行修正；最后，将各分量预测结果进行加和得到时间序列的预测结果.该模型的优势：（1）引入三支决策理论对残差进行修正；（2）通过修正残差来修正余项预测结果；（3）提升时间序列的预测精度.实验结果表明，3WREA 在余项预测任务中效果显著，DT‐LGBM‐3WREA 在多个数据集上取得了比其他模型更优的预测结果.未来将进一步寻找更优的方法确定最佳阈值对(α，β)，并在更大规模的数据集上验证模型的有效性.