面向电大多尺度模型的大规模并行对称半正定亚网格FDTD 算法

陈晓洁，鲍献丰，李瀚宇，张爱清，周海京

（1.中国工程物理研究院 高性能数值模拟软件中心，北京 100088；2.北京应用物理与计算数学研究所，北京 100094）

飞机、舰船等平台电磁环境效应仿真，以及大型阵列天线和天线罩辐射特性仿真等问题均面临计算模型电大尺寸多尺度瓶颈[1−3]，而大规模并行技术是解决这一瓶颈问题的最有效手段[4−5].与有限元和矩量法相比，时域有限差分（finite difference time domain，FDTD）方法在时域和空域上均采用显式迭代，其计算规模和计算能力不受解法器限制，具备天然的高并行可扩展性，因此大规模并行FDTD 在实际工程中应用广泛[6−7].

然而，在实际工程应用中，受到计算资源和成本限制，需要尽可能降低内存需求和计算时间，实现“高效”求解.对于电大多尺度模型，采用非均匀网格剖分可以降低内存需求.但是，由于稳定性条件的限制，FDTD 算法的时间步长取值由最小网格尺寸决定，导致针对多尺度模型的时间步数较多，计算时间较长.无条件稳定FDTD 方法可使得时间步长取值不受稳定性条件的限制，但是隐格式无条件稳定FDTD方法需要求解大规模矩阵方程[8]，显格式无条件稳定FDTD 方法需要求解特征矩阵方程[9]，二者均失去了传统FDTD 方法高并行可扩展性的优势，难以实现大规模并行计算.另一方面，亚网格FDTD 方法采用粗网格剖分整个计算区域，并在包含精细结构的区域采用细化网格进行局部剖分.与基于带状非均匀网格剖分的FDTD 方法相比，其不但可以降低内存需求，还可以在粗网格区域和细化网格区域分别采用大、小时间步长迭代，且不需要求解矩阵方程或特征矩阵方程，在提高计算效率的同时，还保留了传统FDTD 方法的高并行可扩展性优势，因此并行亚网格FDTD 方法是高效解决电大多尺度模型电磁仿真问题的有效手段.

本文针对电大多尺度模型“高效”电磁仿真需求，基于对称半正定亚网格FDTD 算法[10]，通过提出融合JASMIN 并行框架[11]h-自适应时间积分算法流程的亚网格FDTD 算法流程，实现了具备大规模并行能力的亚网格FDTD 算法.该算法采用粗、细两个网格层分别存储整个计算区域网格和局部区域细化网格，并将两个网格层均衡地划分为多个网格片，以网格片为单元实现线程−进程两级并行.同时，算法支持粗、细网格层分别采用大、小时间步进行时间步进.数值计算结果表明，并行亚网格FDTD 算法具有较高的精度和并行可扩展性，与并行均匀网格FDTD算法计算结果相比，其计算效率可提高数10 倍，具备广阔的实际应用前景.

1 对称半正定亚网格FDTD 算法

本文简要介绍对称半正定亚网格FDTD 算法[10]的原理.分别采用下标c和f定义粗网格和细网格场量，下标i和b定义粗细网格内部和粗细网格边界场量，即eci和ecb分别表示粗网格内部电场和粗细网格边界处粗网格电场，efi和efb分别表示细网格内部电场和粗细网格边界处细网格电场，其位置关系如图1所示.

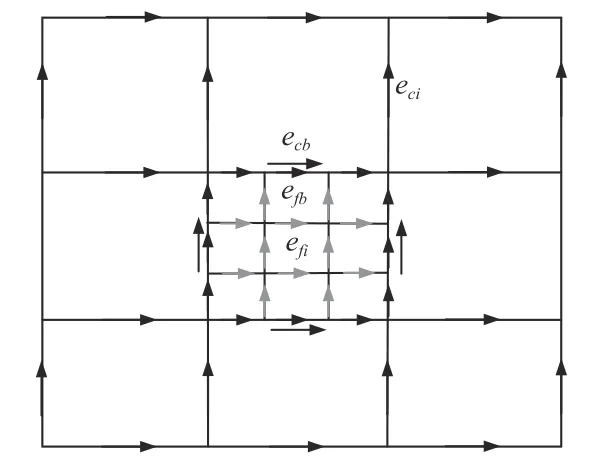
图1 亚网格上场量的位置关系Fig.1 Position relation of field quantities in the sub-grid region

定义电场向量

其中Ne=#eci+#ecb+#ecf，Ne,sub=#eci+#efb+#ecf.定义插值算子矩阵P满足

将式(1)和(2)代入式(3)，则插值算子P可写成如下形式

式中，矩阵Pfc反映了粗细网格边界处粗网格电场和细网格电场的插值关系，即

将时域Maxwell 方程中的电场和磁场分量对空间偏导数采用中心差分格式离散，电场方程两边对时间t求偏导数后将其代入磁场方程，并基于式(4)对插值算子的定义，可得到如下形式的亚网格FDTD算法矩阵方程[10]：

式中，Dε和Dσ分别为介电常数和电导率形成的对角矩阵，

式中：Dµc和Dµf分别为粗、细网格磁导率形成的对角矩阵；Sh,c和Se,c与 粗网格区域空间步长相关；Sh,f和Se,f与细网格区域空间步长相关.由FDTD 算法的稳定性条件可知，若式(6)的矩阵Ctotal为对称半正定矩阵，则其特征值全部为实数，选择适当的时间步长，算法将满足收敛性条件.由于Dε为 对角矩阵，只要Stotal为对称半正定矩阵，则Ctotal必为对称半正定矩阵.因此，只要插值算子P的选择可以保证Stotal为对称半正定矩阵，则该插值方法必是稳定的.

基于上述分析，对称半正定亚网格FDTD 算法在粗细网格层内部均采用传统的FDTD 方法实现电场和磁场迭代，在粗细网格层边界需采用以下两个步骤实现粗、细网格层电场数据的插值和交换.

步骤1：粗细网格边界处粗网格到细网格的电场数据细化.

粗细网格边界处，细网格电场包含两部分，一部分位于与粗网格电场所在边重合的位置，记为efb,e，另一部分位于粗网格面上，记为efb,f.如图2 (a)所示粗细网格交界面处，在ecb已 知的情况下，efb,e可直接取与其所在边重合位置的ecb，efb,f可基于ecb,1与ecb,2线性插值计算得到.因此，矩阵Pfc第i列为

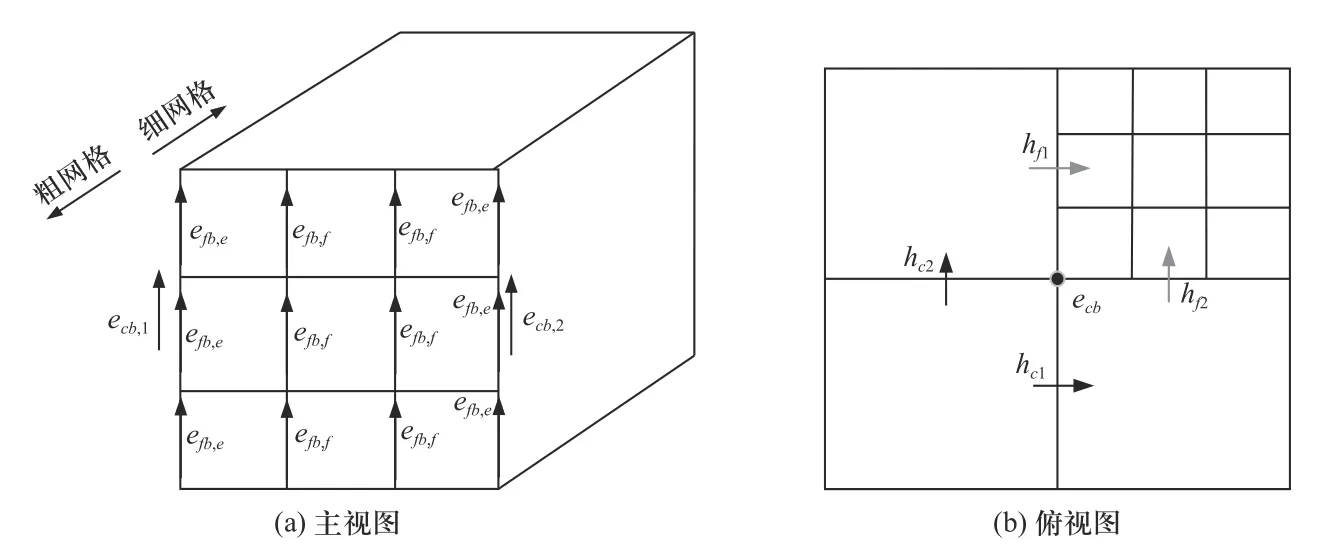
图2 粗细网格边界处电磁场分布示例Fig.2 Example of the electromagnetic field distribution at the boundary of the coarse and fine grids

步骤2：细网格层到粗网格层的电场数据粗化.

在粗细网格边界上，粗网格电场ecb的迭代求解同时涉及粗、细网格上的磁场分量，如图2 (b)所示.因此，可将ecb分解为两部分

式中：ecb,p为粗网格磁场的贡献部分，可基于粗网格磁 场hc1和hc2进 行 迭代求 解；ecb,m为细 网格磁场的 贡献部分，其求解涉及两个过程，一是基于细网格磁场插 值得到 图2(b)所示hf1和hf2，二是基 于hf1和hf2进 行迭代求解.第一个插值过程涉及式(8)右端第二项(PTP)−1PTSf f P，其采用的插值方法是保证算法稳定性的关键.若直接将步骤1 的矩阵P代入式(8)，难以保证Stotal是对称半正定矩阵.因此，为了确保稳定性，需要基于式(11)，对式(8)的具体实现进行适当修正，使其满足对称半正定条件.具体修正过程可参见文献[10]，在此不再赘述.

2 大规模并行实现

本文基于北京应用物理与计算数学研究所自研JASMIN 框架[11]实现亚网格FDTD 算法的大规模并行计算.JASMIN 框架软件体系结构如图3 所示，包括并行计算支撑层、数值共性层和应用接口层.JASMIN 框架屏蔽了结构网格的大规模并行和网格自适应计算技术，支持应用软件开发人员“并行思考、串行编程”地研制高效使用超级计算机的超级并行应用软件.

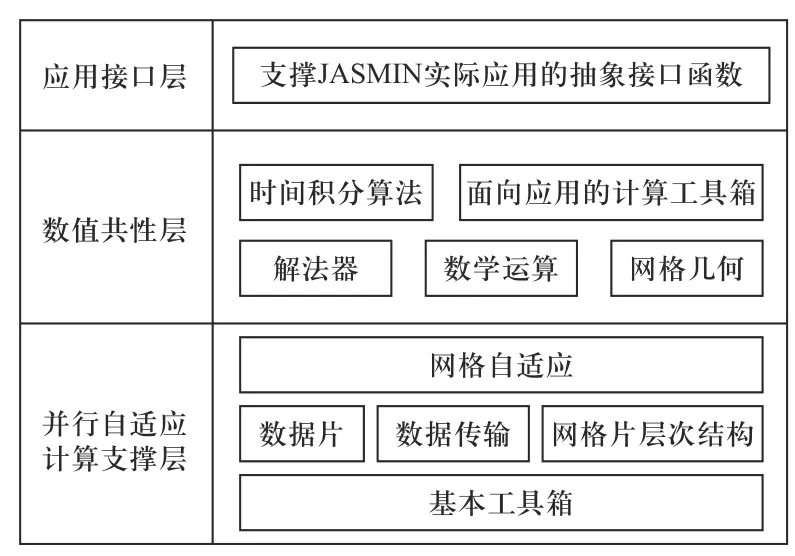
图3 JASMIN 框架软件体系结构Fig.3 Software architecture of JASMIN framework

JASMIN 框架的自适应结构网格由嵌套的多个网格层构成，每个网格层被划分为多个网格片，物理量均存储于网格片上，以网格片为单元实现线程-进程两级并行.基于JASMIN 框架实现传统FDTD 算法时，只需要定义单个网格层.而亚网格FDTD 算法则需要定义两个网格层，分别为粗网格层和细网格层，前者包含整个计算区域，后者只包含精细结构区域.粗网格层和细网格层分别被划分为多个网格片，这些网格片被分配到各个CPU 进行独立计算，基于网格片存储的物理量数据称为数据片.

对于只包含单个网格层的传统FDTD 算法，JASMIN 框架只需负责在网格片之间执行数据通信操作；而对于亚网格FDTD 算法，JASMIN 框架除了负责在粗、细网格层同层执行数据通信操作外，还需负责粗、细网格层之间的数据传输，这一操作流程由h-自适应时间积分算法完成.h-自适应时间积分算法包含时间同步和时间细化两种模式.前者粗细网格层场量均采用细网格层时间步迭代，后者粗网格层场量采用大时间步迭代，细网格层电磁场采用小时间步迭代.由于时间细化模式的求解效率远高于时间同步模式，因此本文的计算方法和计算结果均基于时间细化模式.JASMIN 框架屏蔽了h-自适应时间积分算法复杂的数据传输实现细节，仅开放了时间、空间细化和空间粗化3 个插值算子接口.理想情况下，亚网格FDTD 算法在粗、细网格层内的FDTD 迭代计算流程与经典FDTD 算法相同，唯一不同之处在于需基于JASMIN 框架提供的接口实现时间插值算子，以及粗化和细化两个空间插值算子，以完成粗、细网格层之间的数据传输.然而，如式（12）所示，为了保证算法的稳定性，对称半正定亚网格FDTD 方法中粗细网格边界处粗网格电场的求解需同时涉及粗、细网格层的磁场，JASMIN 框架提供的粗化插值接口无法满足实际计算需求，必须对FDTD 迭代流程进行整体设计.下面将详细介绍本文基于时间细化模式设计的对称半正定亚网格FDTD 算法迭代流程.

假设粗细网格细化率为M，粗网格层时间步长为 ∆t，则在时间细化模式下，粗网格层电磁场每迭代一步，细网格层电磁场将以时间步长 ∆t/M迭代M步.为了论述方便，在粗网格层上定义内部电场eci和磁场hc，在细网格层上定义内部电场efi和磁场hf，在粗细网格边界上定义ecb、ecb,p、ecb,m和efb.为了实现时间插值和空间插值，ecb、ecb,p和ecb,m在粗、细网格层均需开辟内存.采用ecb（粗）、ecb,p（粗）和ecb,m（粗）表示存储于粗网格层的场量，采用ecb（细）、ecb,p（细）和ecb,m（细）表示存储于细网格层的场量.

基于时间细化模式的亚网格FDTD 算法实现流程如图4 所示.算法1、2 和3 分别具体给出图4 所示粗网格层电磁场迭代一个时间步、细网格层电磁场迭代M个时间步，以及粗化3 个步骤的具体实现方法.

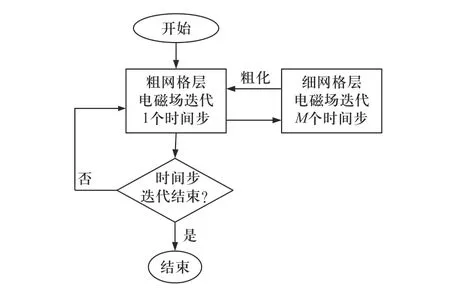
图4 亚网格FDTD 算法实现流程Fig.4 Implementation process of the sub-grid FDTD method

算法1 粗网格层电磁场在第n个时间步的迭代流程

1.粗网格层磁场更新

2.粗网格内部电场更新

3.在粗细网格边界上，粗网格的电场更新

算法1 实现了粗网格层电磁场在第n个时间步的迭代流程.标注2～3 如下，算法2 包含M个时间步迭代流程；其中第1 步和第2 步代码分别基于h-自适应时间积分算法的时间插值接口和空间细化插值接口开发，以完成粗网格层数据到细网格层数据的映射；第3 步～第7 步实现了细网格层电磁场的迭代流程.算法3 中第1 步代码基于h-自适应时间积分算法的空间粗化插值接口开发，以完成细网格层数据到粗网格层数据的映射；第2 步实现粗细网格边界粗网格电场的完整计算.算法2 中第4 步和第7 步实现算法分别为本文第1 节所示对称半正定亚网格FDTD 算法实现步骤1 粗细网格边界粗网格电场到细网格电场的细化和步骤2 细网格层到粗网格层的电场数据粗化.

算法2 细网格层电磁场在粗网格层第n个时间步的M步迭代流程

3 数值算例

3.1 算例1：三维自由空间电磁波传播问题

自由空间区域的左下角和右上角直角坐标分别为(−1.8, −1.8, −1.8) m 和(4.3, 4.3, 4.3) m，其x、y和z方向的空间网格步长均为0.1 m.在空间区域 [(1, 1,1) m, (1.4, 1.4, 1.4) m] 内采用亚网格剖分，网格细化率为20，即亚网格区域x、y和z方向的空间网格步长均为0.005 m.入射平面波沿x轴传播，极化方向沿z轴，其电场分量表达式为Einc=zˆ2(t−t0−x/c)e(t−t0−x/c)2/τ2，c为光速，取值3×108m/s，τ=2×10−8s，t0=4τ.观察点P1和P2的坐标分别为(0.1, 1.3, 1.3)和 (1.3, 1.3, 1.3)，分别位于亚网格区域外和亚网格区域内.

图5 为采用本文的亚网格FDTD 算法的4 核并行计算结果与理论结果的比对，可以看出二者吻合较好.

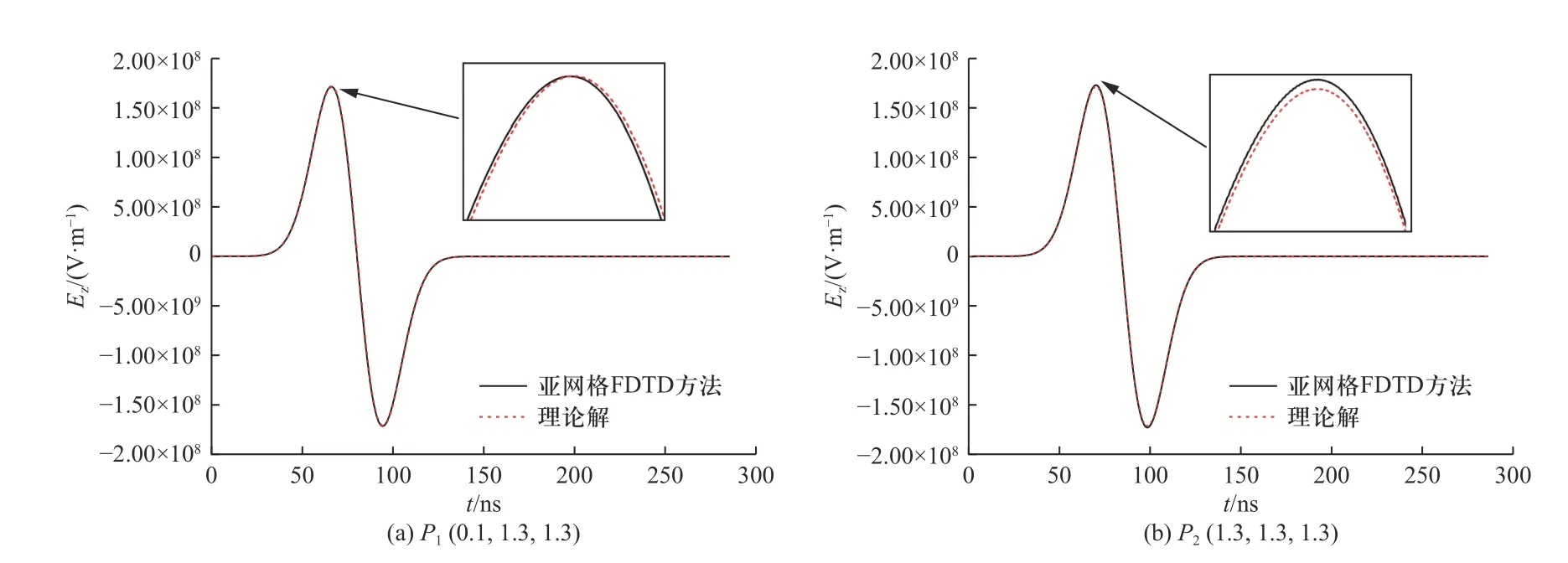
图5 监测点时域电场波形Fig.5 Time domain electric field waveform of the monitoring points

3.2 算例2：多模导弹电磁耦合问题

多模导弹CAD 模型如图6 所示.该模型弹体长度约为6 m，导引头包含天线罩、抛物面天线和线缆等精细结构，天线罩厚度为1.5 mm，其中天线罩为聚四氟乙烯材料，其他部件为理想导体.入射平面波沿-z轴传播，极化方向沿x轴，时域信号源为调制高斯脉冲，其中心频率为1.5 GHz，带宽为3 GHz.包含多模导弹模型的FDTD 计算区域为[(−0.505, −0.505,−0.505) m，(0.5, 0.5, 5.6) m].采用亚网格FDTD 方法计算时，粗网格层网格步长为7.5 mm，网格索引范围为[(0, 0, 0), (133, 133, 813)]，网格总数约为14.6×106；细网格层覆盖整个导引头区域，其计算区域对应在粗网格层的网格索引范围为[(42, 42, 688), (92, 92, 747)]，网格步长为1.5 mm，即网格细化率为5，细网格层总网格数约为19.5×106，因此粗细网格层总网格数约为34.1×106.导引头区域的粗、细网格层计算网格模型如图7 所示.由于导引头区域包含的天线罩、线缆等精细结构，粗网格层无法实现几何模型的精确剖分，出现了结构破损、缺失等现象，引入局部加密的细网格层后则有效避免了上述现象.

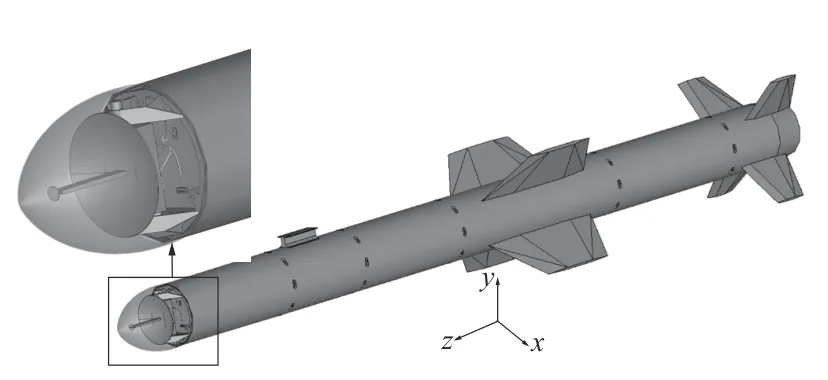
图6 多模导弹CAD 模型Fig.6 The CAD model of the multi-mode missile

图7 导引头区域的网格模型Fig.7 The grid model of the seeker area

为了验证亚网格FDTD 算法的正确性和有效性，采用全局加密的均匀网格FDTD 算法与亚网格FDTD算法的计算结果进行比对.均匀网格FDTD 算法的空间步长与亚网格FDTD 算法细网格层的空间步长一致，为1.5 mm，其总网格数约为998.9×106.两种方法总计算物理时间均为29 ns，亚网格FDTD 算法中，粗网格层计算时间步数约为2 000 步，细网格层时间步数约为10 000 步，均匀网格FDTD 算法的计算时间步为10 000 步.

图8 给出了亚网格FDTD 方法及全局加密均匀网格FDTD 方法计算得到的相同物理时刻导引头附近时域磁场分布伪彩图，可见二者吻合较好；图9 给出了导引头内部监测点的时域电场波形，两种方法计算得到的电场波形吻合较好，由此验证了亚网格FDTD 方法的计算精度和高效性.

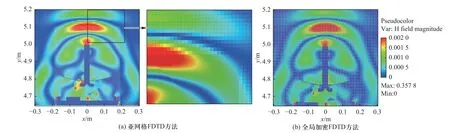
图8 多模导弹导引头附近时域场分布（物理时刻4.3 ns）Fig.8 Time domain field distribution near the missile seeker of the multi-mode (physical time is 4.3 ns)

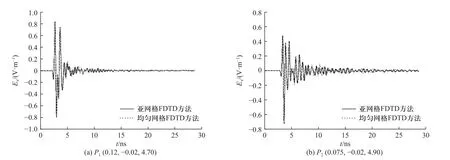
图9 多模导弹导引头内部监测点时域电场波形Fig.9 Time domain electric field waveform of the internal monitoring points of the multi-mode missile seeker

表1 给出了两种方法的计算开销和加速比，其中加速比Sp=T1/Tp，T1为基于1 个CPU 核的计算耗时，Tp为基于p个CPU 核的计算耗时.在相同并行规模下（128 CPU 核并行），亚网格方法内存占用仅为全局加密方法的7%，计算速度提高54.5 倍.由此可见，对于多尺度模型，亚网格FDTD 方法具有较大的性能优势.

表1 亚网格FDTD 方法与均匀网格FDTD 方法计算开销对比Tab.1 Comparison of the computational overhead between the sub-grid FDTD method and the uniform grid FDTD method

为验证亚网格FDTD 方法的并行可扩展性，基于多模弹模型开展了强可扩展并行效率测试（即计算规模保持不变的前提下，改变并行规模），测试得到的并行效率和加速比数据如表2 所示.对于强并行可扩展性测试，随着并行规模的增加，通信耗时占比越来越大.表2 中，虽然当CPU 核数从8 增长到16 时，通信耗时已变成主要矛盾，计算效率陡降，但是128 CPU 核相对于串行计算其强可扩展并行效率仍可达到35%，验证了算法的高并行可扩展性.

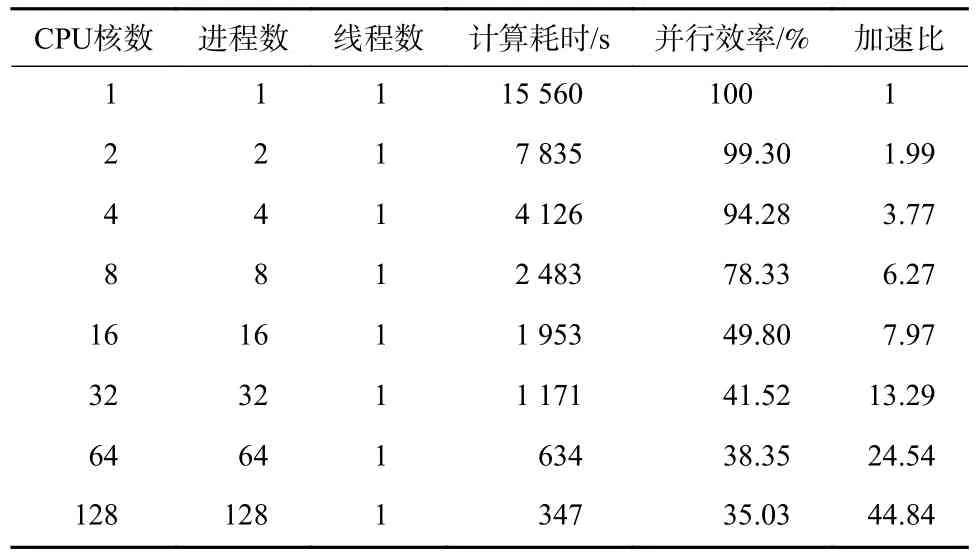
表2 亚网格FDTD 方法并行效率和加速比测试结果Tab.2 Testing results of the parallel efficiency and acceleration ratio of the subgrid FDTD method

4 结 论

本文基于高性能并行计算框架JASMIN，实现了具备大规模并行能力的对称半正定亚网格FDTD 算法.在保证精度和稳定性的前提下，该算法可支持粗网格区域和细网格区域分别采用大时间步长和小时间步长进行迭代计算，且具备高并行可扩展性，可高效地解决电大多尺度模型的电磁模拟问题.数值算例表明，针对电大多尺度模型，本文提出的并行亚网格FDTD 方法可大大减少内存需求，提高计算效率，且具有较高的并行可扩展性，因此具有广阔的应用前景.