基于多模型集成的结构健康状态趋势预测

2023-06-25刘义艳居琳李瑞轩田甜

北京理工大学学报 2023年6期

刘义艳，居琳，李瑞轩，田甜

（1.长安大学电子与控制工程学院，陕西，西安 710064；2.陕西航空电气有限责任公司，陕西，西安 710065）

对服役中的工程结构进行健康状态监测和趋势预测，可以提前获知结构隐患，从而采取相应的措施，以避免事故的发生，减少损失.结构健康状态趋势预测是在已知当前结构状态的情况下，对未来一段时间的结构健康状态进行趋势预测，为判断结构是否发生损伤以及损伤程度提供一个重要依据[1].

要对结构损伤进行早期预测必须选择恰当的时间序列预测方法.长短时记忆单元（LSTM）已经成为循环神经网络（recurrent neural network，RNN）乃至深度学习框架中的一种非常热门的研究模型，并受到了广泛的关注和研究.截止目前，长短时记忆网络已经在拱坝位移监测[2]、网络信息安全监测信息处理[3]、图像处理[4]、轴承寿命预测[5]、飞行器控制[6]乃至气温预测[7]等领域得到广泛应用.但是，LSTM 收敛速度较慢，门控循环单元的参数更新会对整个网络的状态信息造成影响.而深度置信网络（DBN）能够有效提取数据深层次的特征，具有训练速度比较快、避免过拟合问题等优点，且广泛应用于非线性时间序列的预测中.国内外学者和科研机构对DBN 在时间序列预测方面的研究成果主要在以下几个领域：经济领域[8]、自然领域[9]、社会领域[10]、能源领域[11]以及其他领域.但是，当研究的系统逐渐变得复杂时，深度置信网络也暴露出它的部分局限性.

结构健康监测是一个广泛且高度跨学科的研究领域，涉及实验测试、系统识别、数据采集和管理，以及环境和运行条件的长期测量，且研究数据量非常庞大.华林等[12]提出一种基于希尔伯特-黄变换的损伤特征量提取方法，并将该特征量用于结构健康监测，发现基于希尔伯特-黄变换的结构健康监测方法能够有效地识别结构损伤.崔建国等[13]采用局部切空间排序和相关向量机相结合的结构损伤预测模型，实现了复合材料结构损伤预测.

不同的预测模型对同一种结构健康状态趋势预测的能力和产生的误差不同，这就暴露了单一方法预测的局限性，如果将多种方法进行融合，从不同的角度挖掘每一种方法的优势，取长补短，就能达到优于单一方法的目的.为了更好地服务建筑结构系统，精确预测，节约资源，组合预测方法受到越来越多的学者青睐.组合预测是指对同一个问题采用两种或两种以上的预测方法的预测，综合利用各种方法提供的信息，尽可能地提高预测精度，这也是目前工业界的发展方向[14].本文提出了一种运用了加权平均法融合投票法的集成方式，以LSTM、DBN、WNN 作为个体学习器的结构健康状态预测方法，并在工程仿真实验和实际工程振动实验中进行实验研究，对比单一模型，多模型集成预测拥有更高的预测精度.

1 多模型集成预测方法

1.1 个体学习器的选择

集成预测模型综合了个体学习器的优势，为了解决单一算法的局限问题和获取更好的预测结果，需要选择具有差异性、一定预测准确性的个体学习器.DBN、LSTM 是当前比较流行的深度学习方法，小波神经网络（WNN）是一种引入小波变换思想的神经网络模型，它们的数学模型、对时间序列特征信息的提取能力以及长短期的预测精度等方面各有不同，DBN 通过采用逐层训练的方式，解决了深层次神经网络的优化问题，能够有效提取数据深层次的特征，具有训练速度比较快、避免过拟合问题等优点.LSTM 能够有效捕捉长序列之间的语义关联，缓解梯度消失或爆炸现象，同时LSTM 的结构更复杂.WNN 集人工神经网络和小波分析优点于一身，即网络收敛速度快、避免陷入局部最优，又有时频局部分析的特点.这三种模型都广泛使用于时间序列预测.DBN、LSTM、WNN 对非线性、非平稳性时间序列具有很好的学习能力，对结构健康状态的预测有一定的准确性.本文将使用以上三种不同的算法作为集成预测模型的个体学习器，利用个体学习器之间的优势互补，提高结构健康状态预测的精度.

1.2 多模型集成预测方法

为了减少极端值对预测精度的影响，本文将加权平均法和投票法进行融合，以此对多模型集成方法的权值进行选择.对结构健康状态进行预测时，仅仅从个体学习器的预测结果中无法判断预测效果的好与坏，因此利用加权平均法和投票法融合的方式对多模型集成预测的权值系数进行分配[15].该方法在t时刻设置一个集中区间，其中为实际值，θ为允许的误差大小，落在集中区间的预测值，其预测误差小于θ，即与实际值更加接近.设为预测值与实际值之间的绝对误差，当λi>θ时，判定预测结果错误，否则判定预测结果正确.假设有m个个体学习器，对同一个预测值，当第j个个体学习器预测正确时，即预测值落在集中区间，误差也就小于 θ，那么就分配第j个学习器更高的权重，以此来提高模型的预测精度.

将其与算术平均模型产生的预测误差进行对比.假设m个个体学习器在t时刻的预测误差分别为λ1,λ2,···λm，算术平均模型的预测误差 λ¯如式（1）所示

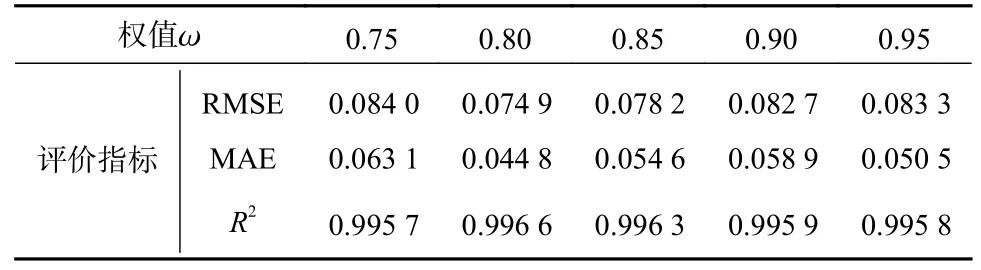
若其中有n（n

多模型集成的预测误差与算术平均模型预测误差的差值 ∆λ如式（3）所示

设t时刻三个学习器的预测值为y1，y2，y3.为了降低预测结果中极端值对集成模型预测结果的影响，将三个学习器的算术平均值y4作为参考值，即第4个学习器，求出 ∆yi=|y4−yi|,i=1,2,3,4 ，设置 ∆yi值最大时的投票结果为预测错误，即yi∉Di，其余的投票为预测正确，即yi∈Di.所以，在t时刻权值的分配公式如式（4）所示

根据投票结果，再利用加权法最终获得多模型集成的预测结果如式5 所示

多模型预测框架如图1 所示.

图1 多模型集成方法框架Fig.1 Structure of multi-model integration method

2 实验结果与分析

为了验证多模型集成的结构健康状态预测方法的性能优劣，将此模型应用到多自由度结构损伤和Phase I IASE-ASCE 结构模拟损伤预测中，研究不同的权值对预测结果的影响，进而选择合适的权值应用到实际工程结构健康状态的预测中.

2.1 三自由度结构健康趋势预测

以三自由度结构为例，图2（a）所示受动力荷载F(t)={F1(t),F2(t),F3(t)}作用的三层框架结构可建立如图2（b）所示的多质点层间剪切结构动力系统模型，图中各质点的质量分别为m1、m2、m3，各层间的刚度分别为k1(t)、k2(t)、k3(t).

图2 三自由度模型Fig.2 Three-degree of freedom (TDOF) structure model

为了减少个体学习器预测结果中的极端值对多模型集成预测精度的影响，采用2.2 节中的方法构造集中区间，对三自由度结构的两种工况：刚度无损伤和第二层刚度下降30%的平均瞬时频率进行实验.由多模型集成算法可知权重的最优取值范围在[0.75,1.00]之间，当权值取0.75 时，多模型集成预测方法的预测结果等于算术平均模型的预测结果.通过对三自由度结构两种工况的预测，研究不同权值 ω对预测结果的影响，表1 是单一预测模型的三自由度刚度无损伤与第二层刚度下降30%预测性能效果，表2和表3 是多自由结构的两种工况在不同权值下的预测效果.

表1 单一预测模型的预测性能评价Tab.1 The evaluation of the damage prediction performance by single prediction model

表2 无损伤的多模型集成预测的性能评价Tab.2 Performance evaluation of multi-model integrated prediction without damage

表3 第二层刚度下降30%的多模型集成预测的性能评价Tab.3 Performance evaluation of multi-model integrated prediction with 30% decreasing stiffness of the second floor

由表1、表2 和表3 中的三种评价指标可知，多模型的预测性能优于任一种单一预测模型.在无损伤工况下，权值 ω=0.80 时，多模型集成预测结果的均方根误差、平均绝对误差最小分别为0.000 81、0.000 73，决定度系数最高为0.991 2；在结构第二层刚度下降30%的损伤工况下，权值 ω=0.80 时，多模型集成预测结果的均方根误差、平均绝对误差最小分别为0.006 8、0.003 4，决定度系数最高为0.945 9.综合多自由度结构两种工况的实验结果可知，ω=0.80时，多模型集成方法的预测效果最佳，其预测结果如图3 所示.

图3 多模型集成方法的预测结果图Fig.3 Prediction results of multi-model integration method

2.2 Phase I IASE-ASCE 结构健康状态预测

为了进一步研究权值对多模型集成预测精度的影响，对Phase I IASC-ASCE 结构模拟的无损伤和有损伤两种工况的平均瞬时频率进行实验.本文运用ASCE 的一座4 层的钢结构框架12 自由度对称模型[16]，见图4.激励为作用于每层y方向的低水平的环境风荷载，分析信号为分别从柱4 的1、2、3 和4 层传感器采集的加速度振动信号，对应为节点13、22、31 和40，采样频率为1 000 Hz，数据长度为16 384.

图4 结构模型柱子的标注、节点编号及检测节点分布图解Fig.4 Structure mode, node number and detection node

通过对ASCE 结构模拟工况的预测，研究不同权值 ω对多模型集成预测结果的影响，表5 和表6 是ASCE 结构模拟的两种工况在不同权值下的预测效果.

由表4、表5 和表6 的三种评价指标的实验结果可知，权值取值在[0.75,1.00]之间时，多模型集成方法的预测误差小于任一单一模型的预测误差.当权值大于0.75 时，多模型集成方法预测的误差小于算术平均预测模型的误差，决定度系数高于算术平均预测模型的精度.ASCE 结构模拟无损伤工况在 ω=0.80 时预测结果的均方根误差最小为0.074 9、平均绝对误差最小为0.044 8，决定度系数最高为0.996 6，相比于ω =0.75，其RMSE、MAE 分别降低了0.91%、1.83%，R2提高了0.09%；ASCE 结构模拟有损伤工况在 ω=0.80 时预测结果的均方根误差最小为0.430 6、平均绝对误差最小为0.222 4，决定度系数最高为0.981 1，相比于 ω=0.75，其RMSE、MAE 分别降低了2.55%、2.51%，R2提高了0.14%.综合ASCE 结构模拟两种工况的实验结果可知，ω=0.80 时，多模型集成方法的预测效果最佳，其预测结果如图5 所示.

表4 单一预测模型的预测性能评价Tab.4 The evaluation of the damage prediction performance by single prediction model

表5 无损伤的多模型集成预测的性能评价Tab.5 Performance evaluation of multi-model integrated prediction without damage

表6 有损伤的多模型集成预测的性能评价Tab.6 Performance evaluation of multi-model integrated prediction with damage

图5 多模型集成方法的预测结果图Fig.5 Prediction results of multi-model integration method

2.3 实际工程结构健康状态预测

由多自由度结构和ASCE 结构的仿真实验可知，权值 ω=0.80时，多模型集成方法预测的效果最好.本小节将此权值输入到多模型集成方法预测的模型中，对实际工程结构的无损伤和取掉东侧所有斜支撑如图6 两种工况的平均瞬时频率进行实验，两种工况的预测结果如图7 所示，表7 和表8 分别是单一预测模型和多模型集成预测模型的预测效果.

表7 单一预测模型的预测性能评价Tab.7 The evaluation of the damage prediction performance by single prediction model

表8 多模型集成预测模型的的预测性能评价Tab.8 Performance evaluation of multi-model integrated prediction

图6 取掉东侧斜支撑工况Fig.6 Prediction results of multi-model integration method for taking out one part of support

图7 多模型集成方法的预测结果图Fig.7 Prediction results of multi-model integration method

由表7 和表8 可以得出，两种权值下模型的预测效果都优于任一单一模型的预测效果.且权值为0.80的预测结果相比于权值为0.75 的预测结果，前者的误差指标最小，决定度系数最高，即 ω=0.80时，无损伤工况的RMSE=0.103 1，MAE=0.084 5，R2=0.988 8，东侧所有斜支柱取掉工况的RMSE=0.124 6，MAE=0.093 0，R2= 0.9901.相比于 ω =0.75时，均方根误差分别降低了0.87%、0.27%，决定度系数分别提高了0.20%、0.04%.因此，权值为0.80 时多模型集成方法在实际工程结构健康状态预测中优于算术平均预测模型和VMDDBN、VMD-WNN、VMD-LSTM 三种单一预测模型.