岩石RHT 本构的爆破碎裂判定方法优化及验证

2023-06-25黄永辉孙博张智宇钱正乾王军李洪超

北京理工大学学报 2023年6期

黄永辉，孙博，张智宇,3，钱正乾，王军，李洪超

（1.昆明理工大学电力工程学院，云南，昆明 650500；2.昆明理工大学国土资源工程学院，云南，昆明 650093；3.昆明理工大学云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室，云南，昆明 650093；4.玉溪大红山矿业有限公司，云南，玉溪 650302；5.昆明理工大学城市学院，云南，昆明 650051）

随着科技发展，爆破理论及技术正在向智能化、精细化方向发展，数值仿真技术作为重要研究手段之一，其关键点在于算法和材料本构，适用于爆破破岩数值计算的算法主要有有限元（FEM）、流固耦合（ALE）、粒子流（SPH）等，材料本构方面主要有TCK、HJC、Yang 及RHT 等.算法和材料本构方程不仅决定计算效率还影响结果的准度，相关研究一直是学术界公认的研究热点.

近年来大量学者[1−8]对岩石损伤本构模型展开了较为系统研究；张若棋等[9]利用AUTODYN 数值软件中混凝土HJC、RHT 本构进行失效强度参数分析计算，提出利用混凝土的特征强度确定失效强度参数的方法并进行校验；王秀丽等[10]采用SPH 法与RHT 本构得到楔挡分流结构在内部爆炸作用下的爆坑形态特征、损伤区范围等；张德生等[11]采用基于光滑质点流体动力学与RHT 混凝土本构的方法得出破碎大块煤的有效方法；PRAKASH 等[12]采用改进后的RHT 本构模型对钢纤维增强水泥基复合材料板（SFRCC）在冲击过程中的各种特性现象得出最佳纤维体积与厚度下的冲击能力峰值；WANG 等[13]提出一种确定RHT 材料模型参数的方法；李洪超等[14]通过正交试验与敏感度分析对RHT 本构中参数进行分析.许多学者[15−22]对爆破荷载下岩石损伤分区判定进行了研究，卢文波等[23−25]利用RHT 损伤本构进行数值模拟，并辅以相应的现场爆破试验，对深部隧道开挖爆破下的岩石损伤孕育机理进行较全面研究；潘城等[26]通过SHPB实验与室内爆破试验对光面爆破参数进行优化，有效控制了超欠挖现象.宋肖龙等[27]利用地质雷达信号具有短时非平稳的特点，通过HHT 法对信号进行去噪处理以提取有效反映损伤特征的瞬时参量，从而获得围岩损伤图像来进行损伤分区.刘闽龙等[28]建立各向异性动态损伤本构进行隧道爆破损伤影响数值模拟，并基于声波测试原理对隧道围岩损伤进行测量，以验证各向异性动态损伤本构的准确性.贾海鹏等[29]建立了损伤敏感区间计算模型，结合实际工况计算出了敏感区间的数值，并校核了区间内外的安全药量.

史卜涛等[30]基于广义插值物质点法提出一种物质点强度折减法，为边坡的稳定性分析提供了新的分析思路；张忠等[31]将点火增长方程与物质点法相结合，对多种材料在撞击屏蔽炸药方面进行模拟，验证了物质点法在冲击起爆问题的可行性；张芮瑜等[32]针对强夯作用下的土体变形问题，将应力密度相关土体本构模型与物质点法相结合，分析总结出强夯过程中的能量转化规律，为相关问题的研究提供新视角；王宇新等[33]基于冲击动力学与爆炸焊接理论，利用物质点法对界面波进行数值模拟并进一步分析研究了界面波形成机理.张智宇等[34]利用高速摄影仪对爆破破岩的物质点进行轨迹抓拍，得到了不同时刻的鼓包运动轮廓.

物质点法在大变形、高速碰撞等方面的模拟效果表现良好，但目前对现场爆破效果分析方面的应用相对较少；RHT 损伤本构在爆炸荷载下对于材料的损伤状态描述方面较为突出，然而岩石损伤的判定准则主要还是基于《水工建筑体地下开挖工程施工技术规范》[35]中的判定标准，判定方法需要进一步优化.本文将从RHT 本构的损伤定义出发，结合岩石损伤破裂理论与损伤判定准则，对变钠质熔岩在爆炸荷载下的岩石碎裂范围进行推导，选取物质点法（material point method）的数值算法，通过数值模拟与现场爆破漏斗试验相结合的方式验证了判定范围的准确性.

1 爆破碎裂区判定方法优化及应用

1.1 判定方法优化

岩石在爆破荷载作用过程中，炮孔壁附近的岩石受炸药产生的爆轰波影响，一定范围内的岩石被粉碎，此时粉碎区的岩石损伤变量Dcrush=1，而粉碎区之外的岩石，由于爆炸能量的衰减，其造成的损伤逐渐减小，因此根据损伤程度分为岩石碎裂区、损伤扰动区及原岩振动区，不同破坏分区示意图如图1 所示.

图1 破坏分区示意图Fig.1 Failure zone diagram

目前对于岩石碎裂区与岩石损伤区之间的损伤临界值相关方面研究存在不足，根据RHT 内嵌公式中可发现，本构模型中关于损伤参量的描述仅有材料初始损伤值D1及完全损伤值D2，并没有对于岩石临界损伤与碎裂区临界损伤的判定标准.为建立RHT 本构中岩石临界损伤参量与本构模型中参数之间的数学关系，参考吴政等[36]根据现有对于岩石损伤变量D的研究成果结合岩石材料损伤失效准则，对岩石材料损伤失效行为进行研究，将岩石材料其峰值应力强度所对应的损伤值视为岩石临界损伤参量Dcr，而材料破坏主要由材料发生塑性变形导致[37]，因此可由式（1）来表示岩石塑性应变与岩石临界损伤参量的关系：

RHT 本构模型中对于损伤参量D定义为

其中：

对式（1）及RHT 本构函数进行整理，分别选取岩石处于开始压碎时与完全压实时的应力状态分别作为岩石损伤区与岩石碎裂区临界阈值评判标准，可得式（1）中的塑性应变与极限应变为

式（1）～（6）中：εp为塑性应变；εmax为峰值应变；为失效时的塑性应变；∆εp为失效塑性应变和当前塑性

1.2 变钠质熔岩力学试验及RHT 本构参数

研究以大红山铁矿地下爆破工程为背景，试验区域岩石为变钠质熔岩，取样开展室内力学性能测试部分试验过程见图2，获得了主要的物理力学参数，根据RHT 本构参数确定方法的相关文献[38]，获得了变钠质熔岩参数详见表1.

表1 变钠质熔岩RHT 本构参数取值汇总表Tab.1 Summarization table of RHT constitutive parameters of sodium metamorphosed lava

图2 室内岩石力学试验过程Fig.2 Laboratory rock mechanics test process

1.3 变钠质熔岩碎裂区判定

根据学者的研究成果，岩石损伤范围与岩石初始损伤、单孔装药量、爆心距及初始传播频率之间呈复杂的函数关系；参考唐红梅等[39]总结得出的地下工程施工爆破过程中围岩损伤分区中爆心距r与损伤变量D间的关系曲线.

式中：a2和f0分别代表衰减系数、爆破初始频率.

由RHT 本构参数和式（5）、（6）可求得岩石损伤临界阈值Dcr=0.11，岩石碎裂临界阈值Dcf=0.51；由式（7）衰减系数、爆破初始频率取值参考熊海华等[40]研究成果分别取9.5×10−4、47 Hz，获得了RHT 本构爆破损伤判定范围如表2 所示.

表2 RHT 本构爆破损伤判定范围Tab.2 RHT constitutive blasting damage determination range

2 基于物质点法爆破碎裂区数值模拟验证

2.1 物质点算法理论

物质点法[41]通过流体隐式质点法将本构方程改为在各质点上计算的方式，并结合等效积分弱形式，采用质点离散建立动量方程的离散格式，因此称为物质点法.该方法[42]仍采用拉格朗日质点和欧拉网格进行双重描述，它将连续体离散成一组质点，每个质点代表一块材料区域并拥有该区域的质量、速度、应力和应变等物质信息，作为一种完全的拉格朗日质点类方法，在每步中质点和计算网格没有进行相对运动，避免了欧拉法在非线性对流向产生的数值困难，且物质界面易跟踪，因此物质点法在冲击、流固耦合等设计大变形或材料破坏方面的数值计算中效率明显优于有限元法与SPH 法，物质点法示意图如图3 所示.

图3 物质点法示意图Fig.3 Material point method diagram

物质点法无需考虑热交换，仅通过求解动量方程即可确定材料状态，物质点法中连续体的动量方程为

同时其边界控制条件与密度离散化方程为

背景网格节点的运动方程为

式（8）～（11）中：ρ为材料密度；u为位移；σij为Cauchy应力；bi为单位质量下的体积力；δ为Dirac delta 函数；mp、xip分别为物质点p的质量与坐标.

而诸多学者[43−44]对物质点法进行了大量研究与扩展，证明了物质点法在处理大变形问题方面上具有极大的优势，本文使用搭载物质点法和RHT 损伤本构的Peneblast 软件作为后续爆破漏斗数值模拟分析算法.

2.2 模拟方案

根据经验以及现场试验条件开展5 组变埋深爆破漏斗数值模拟，设计参数见表3.

表3 变埋深爆破漏斗试验参数Tab.3 Parameters of variable depth blasting funnel test

2.3 模型及参数

数值仿真软件采用由Fortran90 等语言研发的三维显式物质点法数值仿真软件PeneBlast[45]，该软件能较充分体现物质点法在处理大变形方面模拟的优异性，同时支持RHT 本构和炸药本构.构建等比例1/4 对称模型，具体尺寸为1.6 m×1.6 m×2.0 m，对称面采用对称约束，除自由面外的其他边界采用无反射约束.模型见图4.岩石本构参数见表1，炸药采用2 号岩石乳化炸药，其本构参数见表4.

表4 2#岩石乳化炸药参数Tab.4 Parameters of 2# rock emulsion explosive

图4 数值模型Fig.4 Numerical model

2.4 模拟结果分析

（1）爆破漏斗成型过程.

数值计算完成后对等效塑性应变进行输出，爆破漏斗动态成型过程如图5 所示.由图5 可以看出，在t=3.75～60 ms 时，粉碎区初步形成，粉碎区的平均等效塑性应变约为2，以压缩破坏为主；当t=90～120 ms时，应力波到达自由面并在自由面处发生反射拉伸波，粉碎区基本成型，岩石碎裂区与自由面被抛出部分的岩石等效塑性应变高达6.4；t=150 ms 时，爆破漏斗中各损伤分区基本成型，根据等效塑性应变的云图显示，碎裂区岩石的等效塑性应变平均为6.2.

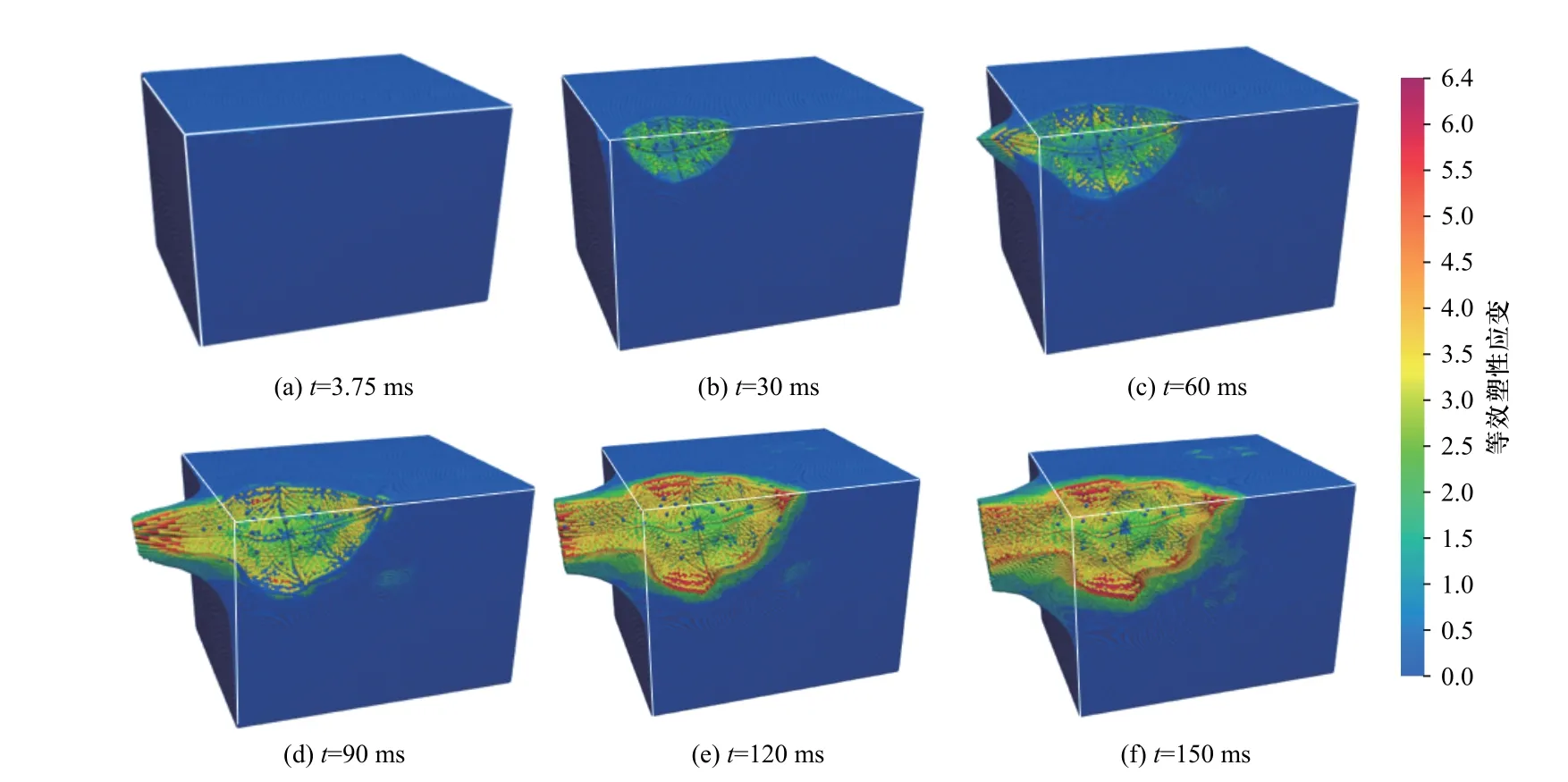
图5 爆破漏斗动态成型过程Fig.5 Dynamic forming process of blasting funnel

（2）爆破漏斗破碎分区规律.

将被抛掷的物质点隐藏处理，并根据文中推导出的判定范围对碎裂区与损伤区进行范围标定，详见表5 中，各组爆破漏斗数值结果与损伤范围分析曲线如图6 所示.

表5 爆破漏斗数值模拟数据Tab.5 Numerical simulation data of blasting funnel

图6 爆破漏斗数值结果Fig.6 Numerical results of blasting funnel

由表5 和图6 可知：粉碎区、碎裂区、损伤区平均半径分别为502 mm、830 mm、1 182 mm，均在理论半径值所划分范围内.随着埋深的增加，各分区半径呈现出先增大后减小的变化趋势，分区半径在埋深为590 mm 时达到最大，而后半径中等幅度减小；粉碎区深度相比炮孔深度多出7.5%～12.3%.粉碎区半径随着埋深的变化幅度较小，其主要是爆炸产生的能量主要向自由面方向传播，而埋深对爆轰波以及爆生气体的膨胀作用影响较小所导致.

碎裂区形状呈类水滴状，炮孔轴向的碎裂区深度在757～941 mm 之间，超出炮孔深度34.4%～51.4%，岩石以压缩破坏为主，基本无自由面效应；炮孔径向的破碎区半径随着埋深的增加存在一定规律，在数值模拟结果中提取距自由面不同深度破碎区范围见图7，可知：接近自由面位置碎裂区半径值最大，之后随着深度增加，呈现下降趋势；通过结果数据拟合后获得了碎裂区半径rds随自由面距离df的变化规律为

图7 碎裂区半径变化趋势Fig.7 Radius variation trend of fracture zone

（3）爆破漏斗体积变化规律

对各组别的爆破漏斗进行可视化处理并计算其体积，结果如图8 所示，可以看出：爆破漏斗体积呈先增大后减小的趋势，在埋深为590 mm 时达到最大.数据显示，粉碎区半径为装药半径的18.8～30.6倍，碎裂区半径为装药半径的36.2～40.4倍，损伤区半径为装药半径的51.3～70 倍，符合爆破动力学[46]中岩石爆破的碎裂区、粉碎区半径确定公式的理论值.

图8 爆破漏斗模拟体积Fig.8 Simulation volume of blasting funnel

3 碎裂区范围现场爆破试验验证

3.1 现场爆破试验情况

为验证数值模拟过程中RHT 本构碎裂区判定范围的可靠性，在大红山铁矿400 m 中段8 号穿脉巷道侧壁进行多组变埋深爆破漏斗试验，钻凿工作采用气腿式凿岩机，有效控制偏斜与钻孔深度误差，设计试验按照数值仿真方案中的参数，共开展5 组，每组3 个孔，孔间间隔2.5 m 以上，爆破漏斗试验场地以及所用爆破器材如图9 所示.

图9 爆破漏斗试验现场及所用设备Fig.9 Blasting funnel test site and equipment

3.2 爆破结果分析

爆破后采用先进的高精度Maptek SR3 三维激光扫描仪对爆破漏斗进行扫描，通过后处理软件对爆破漏斗体积进行可视化处理，爆破漏斗试验效果及数据统计分析结果如图10 所示.由试验结果可知：爆破漏斗形状较不规律，部分存在大块脱落的现象，爆破漏斗半径约为装药半径的22～30 倍；同数值模拟结果相比存在普遍偏大现象，各项平均拟合度分别为91.3%、89%、81.3%，整体拟合度较高，证明RHT碎裂区判定范围具有一定的可靠性.