利用Dandelin球研究“抛物线”的概念教学设计

郝培德

摘要：本文基于分析当前教学实际，利用Dandelin球研究“抛物线”的概念，让学生经历在探究的过程中形成整体的思维意识，提升学生思维及认知水平，发展数学核心素养，落实“四基”.

关键词：单元；教学设计；抛物线

中图分类号：G632文献标识码：A文章编号：1008-0333（2023）15-0053-03

1 背景

数学课程要讲逻辑推理，更要讲道理，通过典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程，体会蕴涵在其中的思想方法，追寻数学发展的历史足迹，把数学的学术形态转化为学生易于接受的教育形态，圆锥曲线单元教学打破圆锥曲线传统概念教学：提出概念（平面）——推导标准方程——练习巩固，利用Dandelin球来研究抛物线的定义.

2 意义

改变传统概念教学模式，利用探究式教学模式，为学生形成积极主动的、多样的学习方式进一步创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯.高中数学课程应力求通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程，发展他们的创新意识.

3 目标

通过回归人们对圆锥曲线的认知规律，重新设计本模块的教学，让学生在学习的过程中不断地经历直观感知、观察发现、归纳类比、空间想像、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维过程提高学生的数学思维能力.

研究内容：研究圆锥曲面和平面交线的形状，得到抛物线的概念，并量化圆锥面和平面交线的形状.

4 教学过程

4.1 教学目标

4.1.1 知识与技能目标

（1）理解怎么由平面与圆锥曲面得到抛物线；

（2）掌握抛物线的定义及抛物线标准方程；

（3）体会平面与圆锥曲面相对位置的变化所得到的曲线类型的一般规律.

4.1.2 过程与方法目标

在得到抛物线之后，利用前面椭圆和双曲线的研究方法来类比研究抛物线的定义，在研究过程中找到异同；同时通过动态演示平面与圆锥曲面的相对位置关系，总结一般规律.

4.1.3 情感目标

通过探究过程引导学生勇于提出问题并且学会如何利用现有的知识解决问题，唤醒学生追求真理，勇于探索的情感需求.

4.2 教学重难点

重点：抛物线的定义、平面与圆锥曲面相对位置的变化所得到的曲线类型的一般规律.

难点：由双球到单球，抛物线定义的推导证明.

4.3 教学过程设计

【知识回顾，引入新知】

利用GeoGebra软件动态展示平面与圆锥曲面交线类型：（如图1）

预设问题：在动态过程中，同学们有没有观察新的曲线？它是在什么位置出现的？

学生回答：当平面与圆锥曲面一条母线平行时会出现单只曲线.这样得到的曲线称之为抛物线（黑板板书抛物线的几何定义：当平面α平行于圆锥面的一条母线m形成的交线）

预设问题：我们现在所定义的抛物线和初中所学的抛物线是一样的吗？

【探究新知】我们根据抛物线的特点，它和椭圆与双曲线相同点是：它们都是平面与圆锥曲面的交线，它们都有Dandelin球；不同点：抛物线只有单球.所以在探究的时候有异同.

类似的找出球与面的切点F和抛物线上任意一点P，接下来我们要在平面α上找出与PF相等的特殊线段.

预设问题：你从图形中可以得到哪些信息？

（提示：定性：平行，对称…；定量：长度，角度…）

学生回答：一组线面（平面和那条特殊的母线）平行；对称（关于母线和轴截面对称）.

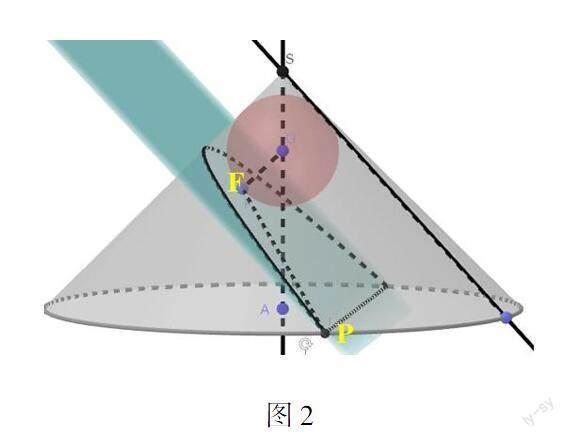
预设问题：你能从图2中找到和线段PF相等的线段吗？

学生回答：没有.

预设问题：那么我们能不能做出线段和线段PF相等，怎么做？大家类比椭圆与双曲线的研究做出这条线段. （下发学案让学生“纸上添画”）

学生回答：连接PS与球相切于点Q，PF=PQ.

预设问题：为什么PS与球相切？

学生回答：因为直线是圆锥曲面的母线，球与圆锥曲面相切.预设问题：现在我们找的了特殊线段PQ，但是这条线段与平面α是有夹角的，

那么如何转移到平面上去？（提示大家看黑板上由那条特殊的线）

学生回答：母线m与平行平面平行，可以再母线上找.

接下来学生在学案上作图.

学生回答：PF=PQ=P0Q0

预设问题：为什么PQ=P0Q0？

学生回答：因为Q与Q0是在且于圆锥曲面的切线上，PQ和P0Q0是圆台的母线所以相等.

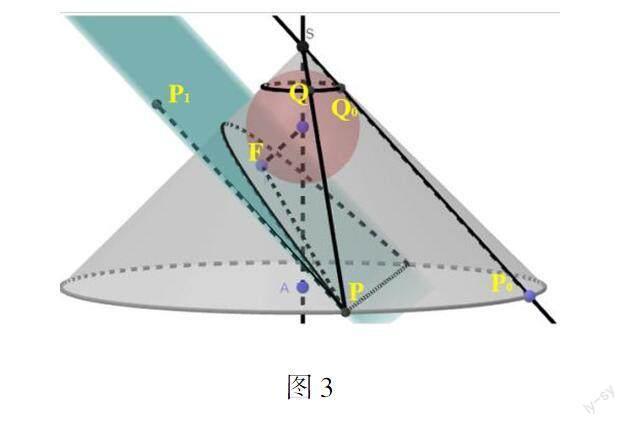
预设问题：下面我们是否可以再平面α上找到线段PP1和PF相等？

学生回答：如图3，在平面α上做PP1与P0Q0平行且相等；

（追问为什么可以画出来……线面平行的性质）

预设问题：点P1是否还能再精确的定位？类比上述过程在曲线上多找出几个点进行研究.

（1） 找点P的对称点M，对应找出M1

（2） 再取曲线上另外的点N，按上述过程找出对应的N1

学生回答：如图4，P1，M1，N1三点共线，设为l，直线PP1，MM1，NN1相互平行.

预设问题：直线l和点P1的定位是否能再精确？

学生回答：略.

【总结定义】（板书）如图6，在平面内，与一个定点F和一条定直线l（l不经过点F）的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点，，直线l叫抛物线的准线，设焦准距p.

预设问题：和我们初中学习的抛物线是一样的吗？接下来大家在学案上建系求方程.

学生回答：如图7，以为直线l为x轴，过F作直线l的垂线为y轴求出的方程是：y=x22p+p2

我們发现它就是初中所学的抛物线.我们也可以如下图建系求方程：

得到抛物线标准方程：x2=2pyp>0.

预设问题：初中所学抛物：形如y=ax2+bx+c（a≠0）的二次函数图象是一条抛物线， 能否找到它的标准形式？

学生回答：略.

进一步总结定义：如图8，在平面内，与一个定点F和一条定直线l（l不经过点F）的距离相等的点的轨迹叫抛物线. PFdP-l=1

4.4 教学反思

本节课是圆锥曲线概念的教学，学生们在前椭圆、双曲线概念课的基础上已基本掌握利用Dandelin双球研究椭圆、双曲线的概念，同时熟知：“发现问题——建立模型——研究问题——总结规律”的顺序研究问题，最后如何生成三类圆锥曲线进行对比分析，得到规律，提升概念课，完成总结任务.在探究的过程中，提升学生解决问题、总结规律的能力.

参考文献：

［1］ 孔繁晶.指向深度学习的单元起始课教学实践与思考：以“复数”单元起始课为例[J].中学教研（数学），2022（02）：12-16.

[2] 蒋梅.单元整体视角下的章起始课教学实践与思考[J].中学数学教学参考，2022（08）：8-10.

［责任编辑：李璟］