基于深度学习的城市快速路交通运行状态判别与预测

赵彪 刘晓锋 付甜

摘  要：为了实时判断城市交通及快速路交通状况，并充分考虑到快速路及交通系统的模糊性、差异性、波动性，文章首先给出了一套基于模糊C均值聚类法（Fuzzy C-Means）的快速路交通状况判断算法，将道路的交通状况区分为通畅、基本顺畅、缓行、堵塞4类。其次，利用了长短期记忆网络（LSTM）的长短时预测技术，给出了一个基于深度学习的模式，对交通运行三参数进行预测，并利用路侧检测设备不断获取新的真实数据，对预测模型进行迭代训练。然后利用已形成的模糊聚类模型，得到快速路交通运行状态的预测结果。最后以天津市黑牛城道的真实交通数据进行实验验证，结果表明，文章提出的交通流状态预测模型准确性达到93.22%，能为快速路交通控制提供有效的状态预测。

关键词：城市快速路；模糊C均值聚类；深度学习；LSTM短时预测方法；交通運行三参数

中图分类号：TP391.9    文献标识码：A    文章编号：2096-4706（2023）01-0001-08

Traffic Operation State Discrimination and Prediction of Urban Expressway

Based on Deep Learning

ZHAO Biao， LIU Xiaofeng， FU Tian

（Tianjin University of Technology and Education， Tianjin  300222， China）

Abstract： In order to judge the urban traffic and traffic condition of expressway in real time， and to fully consider the fuzziness， variability， and fluctuation of expressway and traffic system， a set of judgment algorithms of expressway traffic condition based on Fuzzy C-Means is given in this paper firstly， which distinguishes the traffic conditions of roads into four categories： smooth， basically smooth， slow and blocked. Secondly， a model based on deep learning is given to predict the three parameters of traffic operation by using the Long Short-Term Memory （LSTM） long short-term prediction technique， and the prediction model is trained iteratively by continuously acquiring new real data using roadside detection equipments. Then using the developed fuzzy clustering model， the prediction results of the traffic operation state of the expressway are obtained. Finally， the real traffic data of Heiniu Road in Tianjin is used for experimental validation， and the results show that the accuracy of the traffic flow state prediction model proposed in this paper reach 93.22%， which can provide effective state prediction for expressway traffic control.

Keywords： urban expressway; Fuzzy C-Means; deep learning; LSTM short-time prediction method; three parameters of traffic operation

0  引  言

作为都市道路交通的主动脉，城市快速路以其大容量、高效、强联通的特性承载着城市内各个主要功能区域的交通，极大地减轻了城市压力，提升了城市的整体服务质量。对于道路交通的模糊性、随机性、复杂性，实时准确的短期交通流量预测，对快速路的智能控制和管理具有基础性和决定性的作用。

以往的短期交通预测工具，主要可以分成以下三种：参数方法、非参数方法和混合方法。参数化方法包括时间排序方式和卡尔曼滤波[1，2]。焦朋朋等[3]充分利用其对高维特征数据预测精度高以及计算速度快的优势，提出了基于集成学习XGBoost模型的交通流预测。褚瑞娟[4]给出了基于CEEMDAN-IWEP和GWO-LSSVM的运输流组合分析模型，通过CEEMDAN模型可以把原始运输流时间序列划分成若干个比较均匀、简单的本征模态分量的残余误差序列，采用最小二乘支持向量机对重组后的序列和残差分量进行预测，将各LSSVM模型的预测结果相加得到最终的预测结果。张亮亮[5]等人给出了基于阶段特征分析的城市快速路交通运营状况预报方案，运用滑动变异系数的方法将道路运营状况序列细分为几个有不同特征的子序列，并分析了各个特征子序列的自关系，从而建立了门限自回归的道路运营状况多步预报模式。Guo[1]等采用动态的过程方差，生成可行的预测和估计水平间隔，运用改进的自适应卡尔曼滤波方法预测交通流。Lin[6]基于交通流理论，将ARIMA模型与GARCH模型相结合，得到相应的波动特征，实现高速公路交通流预测。Shahriari[7]将bootstrapping抽样方法和ARIMA结合，建立E-ARIMA交通流预测模型。

传统的基于机器学习的方法利用人为的特征来捕捉交通流的特征，这不足以获得准确的预测性能。此外，早期基于神经网络的工作通常使用浅层网络或只有一个隐藏层，这也无法捕捉交通流的不确定性和复杂的非线性。与传统的ANN模型相比，深度学习模型使用多层架构，从大量的原始数据中自动提取固有的特征。最近，深度学习激发了交通研究的兴趣。不同的深入了解模式，也被引入于交通流分析。然而，现有的基于深度学习模型的交通流预测工作存在以下缺点：

（1）很多作品的着眼点在于单参数的预测，比如交通量预测、交通速度预测，但往往缺乏对整体交通运行情况的控制要素的关注，使得预测结果不能完全反映出交通运行的具体情况，很难在具体的交通管理与控制中作为控制性指标使用。

（2）目前大多数的快速路匝道控制策略研究的主要方法是人工定周期控制和自适应控制。前者无法随交通运行状态的变化而进行实时调整，后者则因为快速路交通系统的复杂性和模糊性而缺乏预见性，因此在国内的推广相对较慢。同时目前的研究缺乏对预测参数的归类处理，也就很难开展对不同交通运行状态，如拥堵状态、畅通状态等的针对性交通管理与控制。本文提出的快速路交通运行状态预测方法，可以有效解决这些问题，为快速路交通控制提供支持。

1  基于FCM的快速路交通状态判别

1.1  FCM算法简介

C均值模糊聚类算法[8]由Bezdek和Castelaz于1972年提出，以同类对象相似度最大，不同类别对象相似度最小为原则，将多维数据样本划分为特定类数。具体方法如下：

设X=｛x1， x2，…， xn｝为n元数据集合，xi∈Rs。FCM把X划分为c个子集S1， S2，…，Sc，若用V=｛α1，…，αc｝表示这c个子集的聚类中心，uij表示元素xj对Si的隶属度，则FCM算法的优化目标函数为：

（1）

滿足如下约束条件：

（2）

其中，

（3）

（4）

（5）

式中U={uij}为c×n矩阵，V={α1，α2，…，αn｝为c×s矩阵，xj与αi的距离为dij，本文中距离计算采用欧式距离。m为模糊指数，用来控制分类矩阵U的模糊程度，其取值大于1，m越大，分类的模糊程度越高，在实际的交通运行预测应用中m的最佳范围为（1.5，2.5）。该算法的主过程通过不断迭代收敛，获取目标函数的最小值，隶属度值uij采用拉格朗日乘数法进行计算。

结合式（1）～式（5），即可够得到隶属度矩阵U和聚类中心A以及使目标函数最小化的迭代优选过程。

1.2  基于FCM交通状态判别方法

1.2.1  数据预处理

为增强数据处理的可信度，必须检验原始数据的完善与合理程度，并消除和舍弃不合理的原始数据记载。本文用三参数基本图作为参照，依次绘就占有率—速度、占有率—交通量、速度—占有率的关系图，对部分数据进行校正和剔除[9]。

1.2.2  迭代聚类

通过式（3）、式（4）计算U（k），V（k+1），比较V（k+1）与V（k），如果满足V（k+1）-V（k）≤?的条件，则停止迭代，得到各交通状态的聚类中心，否则，以k=k+1继续迭代分析。

1.2.3  状态判断结果分析

在模拟数据分析中，随机选择了这些信息并和新的城市交通状态聚类中心比较，以确定最有代表性的信息所对应的新交通状况。

状态判别流程如图1所示。

2  基于深度学习的快速路交通运行状态预测

2.1  LSTM算法简介

长短期记忆网络（Long Short-Term Memory， LSTM）是循环神经网络RNN的一个变体[10]，是专为处理学习长期依赖性现象而设计并产生的，对传统RNN的缺陷具有针对性，是当前使用较为广泛的神经网络模型，在时间序列预测、视频信息处理、图像处理及自然语言处理等诸多领域中能达到较好的应用效果。

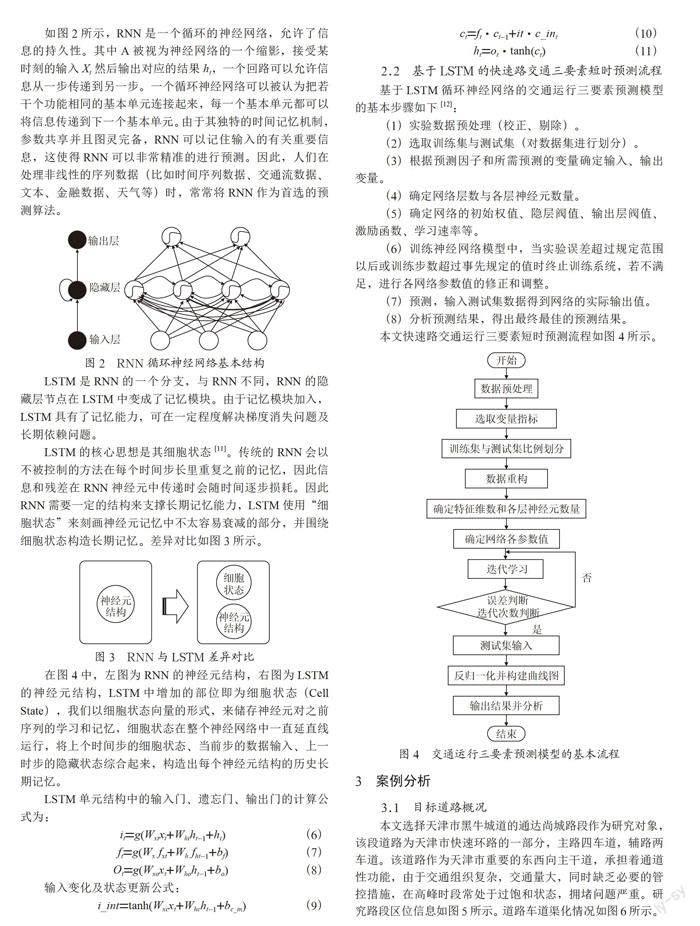
如图2所示，RNN是一个循环的神经网络，允许了信息的持久性。其中A被视为神经网络的一个缩影，接受某时刻的输入Xt然后输出对应的结果ht，一个回路可以允许信息从一步传递到另一步。一个循环神经网络可以被认为把若干个功能相同的基本单元连接起来，每一个基本单元都可以将信息传递到下一个基本单元。由于其独特的时间记忆机制，参数共享并且图灵完备，RNN可以记住输入的有关重要信息，这使得RNN可以非常精准的进行预测。因此，人们在处理非线性的序列数据（比如时间序列数据、交通流数据、文本、金融数据、天气等）时，常常将RNN作为首选的预测算法。

LSTM是RNN的一个分支，与RNN不同，RNN的隐藏层节点在LSTM中变成了记忆模块。由于记忆模块加入，LSTM具有了记忆能力，可在一定程度解决梯度消失问题及长期依赖问题。

LSTM的核心思想是其细胞状态[11]。传统的RNN会以不被控制的方法在每个时间步长里重复之前的记忆，因此信息和残差在RNN神经元中传递时会随时间逐步损耗。因此RNN需要一定的结构来支撑长期记忆能力，LSTM使用“细胞状态”来刻画神经元记忆中不太容易衰减的部分，并围绕细胞状态构造长期记忆。差异对比如图3所示。

在图4中，左图为RNN的神经元结构，右图为LSTM的神经元结构，LSTM中增加的部位即为细胞状态（Cell State），我们以细胞状态向量的形式，来储存神经元对之前序列的学习和记忆，细胞状态在整个神经网络中一直延直线运行，将上个时间步的细胞状态、当前步的数据输入、上一时步的隐藏状态综合起来，构造出每个神经元结构的历史长期记忆。

LSTM单元结构中的输入门、遗忘门、输出门的计算公式为：

it=g（Wxixt+Whiht-1+hi）                         （6）

ft=g（Wx  fxt+Wh  fht-1+bf）                        （7）

Ot=g（Wxoxt+Whoht-1+bo）                        （8）

输入变化及状态更新公式：

i_int=tanh（Wxcxt+Whcht-1+bc_in）                  （9）

ct=ft·ct-1+it·c_int                        （10）

ht=ot·tanh（ct）                            （11）

2.2  基于LSTM的快速路交通三要素短时预测流程

基于LSTM循环神经网络的交通运行三要素预测模型的基本步骤如下[12]：

（1）實验数据预处理（校正、剔除）。

（2）选取训练集与测试集（对数据集进行划分）。

（3）根据预测因子和所需预测的变量确定输入、输出变量。

（4）确定网络层数与各层神经元数量。

（5）确定网络的初始权值、隐层阀值、输出层阀值、激励函数、学习速率等。

（6）训练神经网络模型中，当实验误差超过规定范围以后或训练步数超过事先规定的值时终止训练系统，若不满足，进行各网络参数值的修正和调整。

（7）预测，输入测试集数据得到网络的实际输出值。

（8）分析预测结果，得出最终最佳的预测结果。

本文快速路交通运行三要素短时预测流程如图4所示。

3  案例分析

3.1  目标道路概况

本文选择天津市黑牛城道的通达尚城路段作为研究对象，该段道路为天津市快速环路的一部分，主路四车道，辅路两车道。该道路作为天津市重要的东西向主干道，承担着通道性功能，由于交通组织复杂，交通量大，同时缺乏必要的管控措施，在高峰时段常处于过饱和状态，拥堵问题严重。研究路段区位信息如图5所示。道路车道渠化情况如图6所示。

3.2  交通调查与主要参数

本文主要通过多目标跟踪视觉雷达对汽车目标路线的信息收集，该技术能够实现检测道路的真实汽车跟踪路径信息，包含了汽车的时速、方位、车道号、三维位置，以及超车、变道、停车和逆行等的监测信号，同时具有汽车流量数据、平均速度、市场占有率，以及汽车排队时间等信息。雷达设备安置在该段快速路途中一座人行天桥上，正面面对被测道路，距离道路竖直距离大概7米。系统采用RS485通信模式设置，在多目标跟踪、触发（单目标）和触发（多目标）工作模式下同时发送RS485数据。该系统安装后屏幕架构如图7所示。该多目标雷达采集系统操作界面及检测结果如图8所示。

本文选择的主要研究参数包括交通量、平均运行速度、占有率。同时以一些组合参数对调查时段进行选取，包括堵塞指数（CI）、停止时间比例（PST）等。以120秒为检测间隔，选择早上7：00到8：30作为早高峰时段，中午11：30到13：00作为午高峰，下午5：30到7：00作为晚高峰时段，下午2：50到3：50和上午10：00到11：00作为平峰时段，进行了断面交通调查。各时段总体情况如表1所示。

经过对调查数据的分析，并以后验概率为主要衡量指标在对原始聚类分析法中加以优化，便可得出关于快速路交通运行状况的原始聚类分析法中的4×3阶矩阵。不同交通运行状态的初始聚类中心如表2所示。

3.3  交通运行状态聚类分析

3.3.1  m值的确定

根据m值的选定的取值范围为（1，2.5][13]，采用启发式的方法，以步长0.3在区间（1，2.5]中对进行试取值，即m∈{1.3，1.6，1.9，2.2，2.5}。经过不同m值的效果对比，最终选择m=2.2。

3.3.2  聚类类数c值的确定

在应用算法进行聚类分析时，需要预先给定聚类类数，本文通过聚类有效性函数来确定聚类数目的取值，从而在最大程度上使聚类问题更有效。因而，对聚类分析而言，有效性问题可以转化为最佳聚类类数的确定问题。本文采用类有效性函数，确定不同聚类类数的有效性，类有效性函数如式（14）所示：

（14）

式中，n表示样本数量，c表示类别数，m表示模糊加权指数，xj表示第j个样本的值，uij表示第i个样本对第j类的隶属度，vi、vj表示第i类和第j类的聚类中心。

就模糊聚类的效果而言，同一类别的样本间的相似度越大，分布越紧密，而不同类别的样本间相似度越小，分离程度越大说明聚类效果越好。因此，式（14）中数值越大表示分类的紧密程度越高，分类分离程度越大，p的值越大就表示聚类效果越好。经过计算，c=2，3，4，5，6，7，8，9，10时，有效性函数的函数值如表3所示。